Students can go through AP Inter 2nd Year Physics Notes 2nd Lesson కిరణ దృశాశాస్త్రం, దృగ్ సాధనాలు will help students in revising the entire concepts quickly.
AP Inter 2nd Year Physics Notes 2nd Lesson కిరణ దృశాశాస్త్రం, దృగ్ సాధనాలు
→ కాంతి ఒక శక్తి రూపము. ఇది కంటిపై పడినప్పుడు మనకు దృశా జ్ఞానాన్ని కలిగిస్తుంది.
→ దృగ్గోచర కాంతిని గూర్చి దృశా శాస్త్రంలో అధ్యయనం చేస్తారు.
→ పరావర్తనాన్ని నునుపు తలం నుండి (లేదా) గరకు తలాలు గోడలు, నేల మొదలగు వాటి నుండి పొందవచ్చు.
→ ఎడారులలో ఎండమావులు ఏర్పడుట దృశా ఉదాహరణ.
→ నిజ ప్రతిబింబాలు ఎల్లప్పుడూ తలక్రిందులుగా మరియు మిథ్యా ప్రతిబింబాలు ఎల్లప్పుడూ నిలువుగా ఏర్పడతాయి.
→ పుటాకార దర్పణం ఏర్పరచే ప్రతిబింబం, నాభిని దాటి ఏర్పడదు.
→ పుటాకార దర్పణంలో f మరియు R రెండింటిని ధనాత్మకంగా తీసుకుంటాం.
→ కుంభాకార దర్పణంలో f మరియు R రెండింటిని రుణాత్మకంగా తీసుకుంటాం.
→ నిజ వస్తువులు మరియు నిజ ప్రతిబింబాల దూరాలను రుణాత్మకంగా తీసుకుంటాం.
→ మిథ్యా వస్తువులు మరియు మిథ్యా ప్రతిబింబాల దూరాలను ధనాత్మకంగా తీసుకుంటాం.
→ దర్పణం ఏర్పరచే ప్రతిబింబం నిజ ప్రతిబింబమైతే ఆవర్థనం రుణాత్మకం.
→ దర్పణం ఏర్పరచే ప్రతిబింబం మిథ్యా ప్రతిబింబమైతే ఆవర్థనం ధనాత్మకం.
→ ఉష్ణోగ్రత పెరిగితే వక్రీభవన గుణకము తగ్గుతుంది.
→ మంద కటకానికి నాభ్యంతరము తక్కువగా ఉంటుంది.
→ కాంతి కిరణము వక్రీభవన యానకంపై లంబంగా పతనం చెందినప్పుడు స్నేల్ నియమం విఫలమవుతుంది.
![]()
→ స్నేల్ నియమం ప్రకారం, పతన కోణము సైన్ విలువకు, వక్రీభవన కోణం సైన్ విలువకుగల నిష్పత్తి, వక్రీభవన గుణకానికి సమానం.
→ దర్పణం యొక్క వ్యాసాన్ని, దర్పణం ద్వారం అంటారు.
→ గోళాకార దర్పణం మధ్యబిందువును ధ్రువం అంటారు.
→ ధ్రువం మరియు దర్పణం యొక్క వక్రత కేంద్రములను కలిపే రేఖను ప్రధానాక్షం అంటారు.
→ గోళం యొక్క వ్యాసార్థముతో, దానిలో భాగంగా దర్పణం ఏర్పడితే దానిని వక్రతా వ్యాసార్థం అంటారు.
→ దర్పణం ధ్రువం నుండి ప్రధాన నాభి వరకుగల దూరాన్ని నాభ్యంతరము అంటారు.
→ కథకంపైబడే కాంతిని అభిసరణ (లేదా) అపసరణ చెందించే సామర్థ్యాన్ని కటకం యొక్క సామర్థ్యం అంటారు.
→ వర్షం పడిన తర్వాత సూర్యుడి నుండి వచ్చే తెల్లని కాంతి ఏర్పరచే వర్ణపటం ఇంద్రధనస్సువలె ఏర్పడుతుంది.
→ తెల్లని కాంతి వేరువేరు రంగులుగా విడిపోయే దృగ్విషయాన్ని కాంతి విక్షేపణం అంటారు.
→ హ్రస్వ దృష్టిగల వ్యక్తి దగ్గర వస్తువులను స్పష్టంగా చూడగలడు మరియు దూరపు వస్తువులను స్పష్టంగా చూడలేడు.
→ దీర్ఘ దృష్టిగల వ్యక్తి దూరపు వస్తువులను స్పష్టంగా చూడగలడు మరియు దగ్గర వస్తువులను స్పష్టంగా చూడలేడు.
→ పుటాకార దర్పణం నాభ్యంతరము (f) = \(\frac{R}{2}\)
→ దరణ సూత్రం \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
→ రేఖీయ ఆవర్థనం (m) = \(\frac{I}{o}=\frac{-v}{u}=\frac{f}{f-u}=\frac{f-v}{f}\)
→ స్నేల్ సూత్రం, \(\frac{\sin \mathrm{i}}{\sin \mathrm{r}}\) = μ
→ యానకం వక్రీభవన గుణకం (µ) = \(\frac{c}{v}\)
→ µ = \(\frac{\mu_2}{\mu_1}\), µ2 = \(\frac{1}{{ }_2 \mu_1}\)
→ µ = \(\frac{1}{\sin c}\)
→ \(\frac{-1}{\mathrm{u}}+\frac{\mu}{\mathrm{v}}=\frac{\mu-1}{\mathrm{R}}\)
→ కటక తయారీదారు సూత్రం \(\frac{1}{f}\) = (µ – 1)\(\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
→ కటక సూత్రం \(\frac{-1}{u}+\frac{1}{v}=\frac{1}{R}\)
→ పుటాకార (లేదా) కుంభాకార కటకం రేఖీయ ఆవర్థనం m = \(\frac{I}{o}=\frac{v}{u}=\frac{f}{f+u}=\frac{f-v}{f}\)
→ కటకం యొక్క సామర్థ్యం (P)
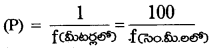
→ రెండు కటకాలు స్పర్శలో ఉంటే, \(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}_1}+\frac{1}{\mathrm{f}_2}\)
→ రెండు కటకాలు కొంత దూరంలో ఉన్నప్పుడు, \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}-\frac{d}{f_1 f_2}\)
→ నమ కటకం సామర్థ్యముP = P1 + P2(రెండూ స్పర్శలో)P = P1 + P2 – dP1P2(కొంత దూరంలో ఉన్నప్పుడు)
→ వక్రీభవన గుణకము (µ) = \(\frac{\sin \left(\frac{A+D_m}{2}\right)}{\sin A / 2}\)
→ విక్షేపణ సామర్థ్యము (ω) = \(\frac{\delta_{\mathrm{v}}-\delta_{\mathrm{R}}}{\delta}=\frac{\mu_{\mathrm{v}}-\mu_{\mathrm{r}}}{\mu-1}\)
![]()
→ సరళ సూక్ష్మదర్శిని ఆవర్థన సామర్థ్యము (m) = 1 + \(\frac{D}{f}\).
→ సంయుక్త సూక్ష్మదర్శిని ఆవర్ధన సామర్థ్యము (m) = \(\frac{\mathrm{v}_0}{\mathrm{u}_0}\left(1+\frac{\mathrm{D}}{\mathrm{f}_0}\right)=\frac{-\mathrm{L}}{\mathrm{f}_0}\left(1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right)\)