AP Inter 2nd Year Physics Study Material Chapter 13 పరమాణువులు

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 13th Lesson పరమాణువులు Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 13th Lesson పరమాణువులు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బోర్ నమూనాలో హైడ్రోజన్ పరమాణువు రెండవ కక్ష్యలోని ఎలక్ట్రాన్ కోణీయ ద్రవ్యవేగం ఎంత?
జవాబు:
హైడ్రోజన్ పరమాణు రెండవ కక్ష్యలో ఎలక్ట్రాన్ కోణీయ ద్రవ్యవేగము L = \(\frac{2h}{2 \pi}=\frac{h}{\pi}\) [∵ L = \(\frac{nh}{2 \pi}\)]

ప్రశ్న 2.
సూక్ష్మ నిర్మాణ స్థిరాంకం (fine structure constant) సమాసం ఏమిటి ? దాని విలువ ఏమిటి ?
జవాబు:

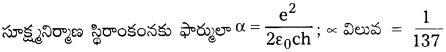
ప్రశ్న 3.
‘ఎలక్ట్రాన్ రుణాత్మక శక్తి’ కి భౌతిక అర్ధం ఏమిటి?
జవాబు:
ఆకర్షణబలం వల్ల ఎలక్ట్రాన్ కేంద్రకంతో బంధించబడి ఉండటాన్ని, ఎలక్ట్రాన్ రుణశక్తి తెలుపుతుంది.

ప్రశ్న 4.
ఒక వాయువు వర్ణపటంలో సునిశిత (Sharp) రేఖలు ఉన్నాయి. ఇది దేనిని సూచిస్తుంది?
జవాబు:
వాయు వర్ణపటంలోని సునిశిత రేఖలు, నల్లని బ్యాక్ గ్రౌండ్్ప వెలుగు రేఖలను తెలుపును.

ప్రశ్న 5.
కోణీయ ద్రవ్యవేగం మితులకు సమానమైన మితులు కలిగి ఉన్న భౌతికరాశిని పేర్కొనండి.
జవాబు:
ప్లాంక్ స్థిరాంకము

ప్రశ్న 6.
α – కణానికి, హీలియం పరమాణువుకు మధ్యగల భేదమేమిటి?
జవాబు:

α – కణము	హీలియం పరమాణువు
1. ఇది + 2 ఆవేశం గల హీలియం కేంద్రకము.	1. ఇది ఆవేశంను కలిగి ఉండదు.
2. ఇది 2 ప్రోటానులు మరియు 2 న్యూట్రానులు కలిగి ఉండును.	2. ఇది 2 ప్రోటానులు, 2 ఎలక్ట్రానులు మరియు 2 న్యూట్రానులు కలిగి ఉండును.

ప్రశ్న 7.
అభిఘాత పరామితికి, పరిక్షేపణ కోణానికి మధ్య సంబంధమేమిటి?
జవాబు:

ప్రశ్న 8.
ఆల్ఫా, బీటా, గామా వికిరణాలలో ఏవి విద్యుత్ క్షేత్రానికి ప్రభావితం అవుతాయి?
జవాబు:
ఆల్ఫా మరియు బీటా వికిరణాలు విద్యుత్ క్షేత్రంలో ప్రభావితం అవుతాయి.

ప్రశ్న 9.
భూస్థాయి పరమాణువు అనే పదబంధాన్ని మీరెలా అర్థం చేసుకొంటారు?
జవాబు:
పరమాణువులో ఎలక్ట్రాన్ భూస్థాయిలో ఉంటే, దానిని భూస్థాయి పరమాణువు అంటారు.

ప్రశ్న 10.
రూథర్ ఫర్డ్ ప్రయోగంలోని పరిక్షేపణలో కేంద్రకం ద్రవ్యరాశికి ఏమాత్రం ప్రాధాన్యత లేదు. ఎందుకు?
జవాబు:
పరమాణు పరిమాణం 10-10 m మరియు కేంద్రకం పరిమాణం 10-15 m. కావున పరమాణువులో ఎక్కువ ఖాళీ ప్రదేశం ఉండును. అందువల్ల రూథర్ ఫర్డ్ ప్రయోగంలో కేంద్రకం ద్రవ్యరాశికి ఎటువంటి ప్రాముఖ్యత లేదు.

ప్రశ్న 11.
హైడ్రోజన్ వర్ణపటంలోని లైమన్ శ్రేణి అతినీలలోహిత ప్రాంతంలో ఉంటుంది. ఎందుకు? [AP. Mar. ’15]
జవాబు:
అతినీలలోహిత ప్రాంత వర్ణపటంలో గణించిన తరంగదైర్ఘ్య విలువలు, హైడ్రోజన్ వర్ణపటం లైమన్ శ్రేణిలో ప్రయోగ పూర్వకంగా పరిశీలించిన తరంగదైర్ఘ్యం విలువలతో ఏకీభవిస్తున్నాయి.

ప్రశ్న 12.
వివిధ వర్ణపట శ్రేణుల దీర్ఘ, హ్రస్వ (longest and shortest) తరంగదైర్ఘ్యాలను ఇస్తూ ఒక పట్టికను రాయండి.
జవాబు:

వర్ణపటం శ్రేణి	గరిష్ఠ తరంగదైర్ఘ్యం λmax Å	కనిష్ఠ తరంగదైర్ఘ్యం λmin Å
1. లైమన్	1216	912
2. బామర్	6563	3646
3. పాశ్చన్	18,751	8,220
4. బ్రాకెట్	40,514	14,585
5. ఫండ్	74,583	22,789

ప్రశ్న 13.
హైడ్రోజన్ వర్ణపటంలోని కొన్ని వర్ణపటరేఖల తరంగదైర్ఘ్యాలు 1216 A, 6463 A, 9546 . వీటిలో ఏ తరంగదైర్ఘ్యం పాశ్చన్ శ్రేణికి చెందినది?
జవాబు:
1956Å తరంగదైర్ఘ్యం ఉన్న వర్ణపట రేఖ పాశ్చన్ శ్రేణికి చెందినది.

ప్రశ్న 14.
రూథర్ ఫర్డ్ పరమాణు నమూనా యొక్క ఏవైనా రెండు లోపాలను ఇవ్వండి.
జవాబు:
రూథర్ ఫర్డ్ పరమాణు నమూనాలో లోపాలు :

1. కక్ష్యలో తిరుగుతూ ఉన్న ఎలక్ట్రాన్ క్రమంగా శక్తిని పరమాణువు కోల్పోతూ, చివరకు కేంద్రకంలో పడి నశించాలి. కాని ద్రవ్యం స్థిరం కాని, పరమాణువు నశించదు.
2. పరమాణువులు అవిచ్ఛిన్న వర్ణపటంను ఉద్గారించాలి. కాని మనం ఒక్క రేఖా వర్ణపటంను పరిశీలించటం జరిగింది.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
అభిఘాత పరామితి, పరిక్షేపణ కోణం అంటే ఏమిటి? అవి ఒకదానికొకటి ఎలాంటి సంబంధం కలిగి ఉన్నాయి?
జవాబు:
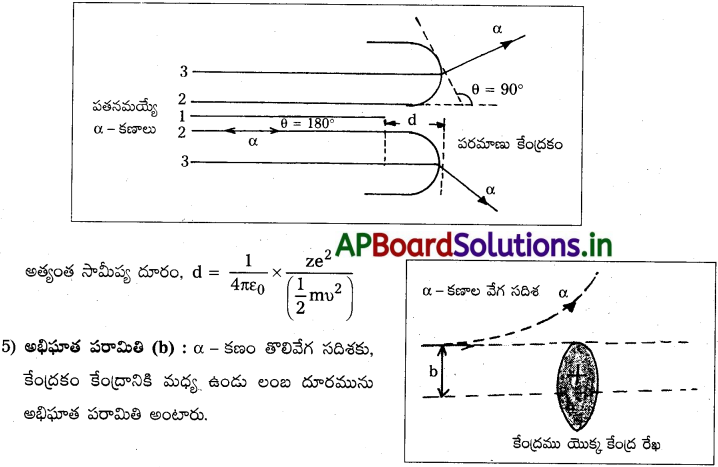
1) అభిఘాత పరామితి (b) :
α-కణం తొలివేగ సదిశకు, కేంద్రకం కేంద్రానికి మధ్య ఉండే లంబ దూరమును అభిఘాత పరామితి అంటారు.

2) పరిక్షేపణ కోణం (θ) : α – కణం కేంద్రకంను సమీపించు దిశకు మరియు విచలన దిశకు మధ్యగల కోణంను పరిక్షేపణ కోణం అంటారు.

ప్రశ్న 2.
బోర్ పరమాణు నమూనా ప్రకారం హైడ్రోజన్ పరమాణువులోని ఏదైనా కక్ష్యలో ఉన్న ఎలక్ట్రాన్ స్థితిజ, గతిజ శక్తులకు సమాసాన్ని ఉత్పాదించండి. n పెరిగే కొద్దీ స్థితిజశక్తి ఏవిధంగా మారుతుంది? [TS. Mar.’15]
జవాబు:
1) బోర్ నియమము ప్రకారము, పరిభ్రమిస్తూ ఎలక్ట్రాన్లకు మరియు కేంద్రకంనకు మధ్య ఉన్న స్థిరవిద్యుత్ ఆకర్షణ బలం F_e, ఎలక్ట్రాన్లు తమ కక్ష్యలలో పట్టి ఉంచేందుకు అభికేంద్ర బలంను సమకూర్చును.

6) ‘n’ పెరిగిన, పొటెన్షియల్ శక్తి (U) కూడా పెరుగును.

ప్రశ్న 3.
హైడ్రోజన్ పరమాణువు యొక్క బోర్ సిద్ధాంతం పరిమితులు ఏమిటి? [AP. Mar.’17; Mar. ’14]
జవాబు:
హైడ్రోజన్ పరమాణువు బోర్ సిద్ధాంతం పరిమితులు :

1. ఈ సిద్ధాంతం, Z = 1 వంటి సరళ హైడ్రోజన్ వంటి పరమాణువులకు మాత్రమే వర్తిస్తుంది. Z > 1 అయిన మూలక పరమాణువుల సందర్భంలో ఈ సిద్ధాంతం వర్తించదు.
2. ఎలక్ట్రాన్ల కక్ష్యలు వృత్తాకారంగా ఎందుకు తీసుకుంటారో వివరించలేదు. ఎలక్ట్రాన్ల దీర్ఘవృత్తాకార కక్ష్యలు కూడా సాధ్యమే.
3. వర్ణపట రేఖల సాపేక్ష తీవ్రతలు గురించి బోర్ సిద్ధాంతం వివరించలేదు.
4. ఎలక్ట్రాన్ల తరంగ ధర్మాలను బోర్ సిద్ధాంతం పరిగణనలోనికి తీసుకోలేదు.

ప్రశ్న 4.
అత్యంత సామీప్య దూరం (distance of closest approach), అభిఘాత పరామితులను వివరించండి.
జవాబు:
అత్యంత సామీప్య దూరం:
1) ఒక α–కణం, తొలిగతిజ శక్తి (K.E) తో పరమాణు కేంద్రకం, కేంద్రం వైపు చలిస్తుందని భావిద్దాం.

2) కేంద్రకము మరియు α-కణంకు మధ్య కూలుంమ్ వికర్షణ బలంను లెక్కలోనికి తీసుకుంటే, α- కణం గతిజశక్తి సమీపిస్తుంటే తగ్గును. తరువాత కణం స్థితిజశక్తి పెరుగును.

3) కేంద్రకం నుండి ‘d’ దూరం వద్ద, α-కణం గతిజశక్తి సున్నాకు తగ్గును. కణం ఆగిపోవును. కేంద్రకంను సమీపించలేదు. కణం, కేంద్రకంచే వికర్షించబడును. కణం 180° తిరిగి వచ్చిన మార్గంను అనుసరించును.

4) ఈ దూరం ను అత్యంత సామీప్యదూరం అంటారు.

ప్రశ్న 5.
థామ్సన్ పరమాణు నమూనాకు ఒక సంక్షిప్త వివరణ ఇవ్వండి. దీని పరిమితులు ఏమిటి?
జవాబు:

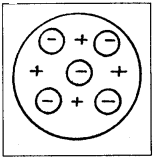
థామ్సన్ పరమాణు నమూనా:

1. థామ్సన్ నమూనా ప్రకారము, ప్రతి పరమాణువు, 10^-10 m వ్యాసార్థం ఉన్న ధనావేశగోళము. దానిలో పరమాణు ద్రవ్యరాశి మరియు ఆవేశం ఏకరీతి వితరణ కలిగి ఉండును.
2. ఈ గోళం లోపల, ఎలక్ట్రాన్లు పుచ్చకాయలోని విత్తనాలవలె లేక ధనావేశం, గుజ్జువలె కలిగి ఉంటుంది.
3. పరమాణువులో ఎలక్ట్రాన్లు కలిగి ఉండే రుణావేశం, పరమాణు ధనావేశంనకు సమానము. కావున పరమాణువు విద్యుత్ పరంగా తటస్థము.

పరిమితులు :

1. ఇది ప్రయోగపూర్వకంగా పరిశీలించిన, మరియు ఇతర పరమాణు వర్ణపట శ్రేణుల మూలంను వివరించలేదు.
2. రూథర్ ఫర్డ్ పరిశీలించిన, పలుచని లోహ పలకల నుండి – కణాలు హెచ్చు పరిక్షేపణ కోణాలను, వివరించలేదు.

ప్రశ్న 6.
రూథర్ ఫర్డ్ పరమాణు నమూనాను వర్ణించండి. ఈ నమూనా లోపాలు ఏమిటి?
జవాబు:
రూథర్ ఫర్డ్ పరమాణు నమూనా : రూథర్ఫర్డ్ గ్రహమండల నమూనాను ప్రతిపాదించాడు.

1. ప్రతి పరమాణువు చిన్న కేంద్రీయ కోర్ను కలిగి ఉండును. దీనిని పరమాణు కేంద్రకం అంటారు. దానిలో మొత్తం ధనావేశం మరియు పరమాణు మొత్తం ద్రవ్యరాశి కేంద్రీకరించబడును.
2. కేంద్రక పరిమాణం 10^-15 m, పరమాణు కేంద్రకం 10^-10m తో పోల్చిన చాలా తక్కువ.
3. కేంద్రకం చుట్టూ నిర్దిష్టమైన ఎలక్ట్రాన్లు ఉండును. పరమాణువులో కేంద్రం చుట్టూ ఉన్న ఎలక్ట్రాన్ల మొత్తం రుణావేశం, కేంద్రకంపై ధనావేశం మొత్తంనకు సమానం. కావున పరమాణువు మొత్తం మీద విద్యుత్పరంగా తటస్థము.
4. గ్రహాలు సూర్యుని చుట్టూ పరిభ్రమిస్తూ ఉన్నట్లే, ఎలక్ట్రాన్లు కేంద్రకం చుట్టూ వేర్వేరు వృత్తాకార కక్ష్యలో పరిభ్రమిస్తూ ఉంటాయి. ఎలక్ట్రాన్ పరిభ్రమించడానికి కావాల్సిన అభికేంద్రబలమును, ఎలక్ట్రాన్ మరియు కేంద్రకమునకు మధ్య ఉన్న స్థిర విద్యుత్ ఆకర్షణ బలం అందిస్తుంది.

లోపాలు :
సాంప్రదాయక విద్యుదయస్కాంత సిద్ధాంతం ప్రకారము,

1. కక్ష్యలో తిరుగుతూ ఉన్న ఎలక్ట్రాన్ క్రమంగా శక్తిని కోల్పోతూ, చివరకు కేంద్రకంలో పడి పరమాణువు నశించాలి. కాని ద్రవ్యం స్థిరం కాని పరమాణువు నశించదు.
2. పరమాణువులు అవిచ్ఛిన్న వర్ణపటంను ఉద్గారించాలి. కాని మనం ఒక్క రేఖావర్ణపటంను పరిశీలించటం జరిగింది.

ప్రశ్న 7.
ఉత్తేజన పొటెన్షియల్ (excitation potential), అయనీకరణ పొటెన్షియల్ల మధ్య భేదమేమిటి?
జవాబు:
ఉత్తేజిత పొటెన్షియల్ :
1) ఒక ఎలక్ట్రాన్ శక్తిని శోషణం చేసి, తక్కువ కక్ష్య నుండి ఎక్కువ కక్ష్యలోనికి దూకి ఎలక్ట్రాన్ ను ఉత్తేజిత ఎలక్ట్రాన్ అని, ఈ ప్రక్రియను ఉత్తేజిత ప్రక్రియ అంటారు. ఎలక్ట్రాన్ లోపలి కక్ష్య (భూస్థాయి) నుండి బయట కక్ష్యలోనికి ఎలక్ట్రాన్ దూకటానికి కావాల్సిన శక్తిని, త్వరణ పొటెన్షియల్ ఇస్తుంది. ఈ పొటెన్షియల్ను ఉత్తేజిత పొటెన్షియల్ లేక అనునాద పొటెన్షియల్ అంటారు.

2) a) ఉదాహరణకు, హైడ్రోజన్ పరమాణు సందర్భంలో E₁ = – 13.6 eV.
E₂ = -3.4 eV, E₃ = -1.5leV ………… E_∞ = 0
∴ ఎలక్ట్రాన్ భూస్థాయి (n = 1) నుండి మొదటి ఉత్తేజిత స్థాయి (n = 2) లోనికి వెళ్ళటానికి కావాల్సిన శక్తి E = E₂ – E₁ = -3.4 – (−13.6) = 10.2 ev.
అనురూప ఉత్తేజిత పొటెన్షియల్ = 10.2 ev.
b) ఇదేవిధంగా, ఎలక్ట్రాన్ భూస్థాయి (n = 1) నుండి రెండవ ఉత్తేజిత (n = 3) స్థాయిలోనికి వెళ్ళటానికి కావాల్సిన
శక్తి E = E₃ – E₁ = -1.51 (-13.6)=-1.51 13.6
అనురూప ఉత్తేజిత పొటెన్షియల్ = 12.09 Volt

3) ఒక పరమాణువు ఉత్తేజిత పొటెన్షియల్ ఒకటికాదు. పరమాణువు ఏ స్థాయిలోనికి ఉత్తేజితం చెందిందో, దానిపై ఆధారపడి, ఇది అనేక విలువలు కలిగి ఉండును.

అయనీకరణ పొటెన్షియల్:

1. పరమాణువు బాహ్య కక్ష్య నుండి ఎలక్ట్రాన్ను తొలగించటానికి కావాల్సిన శక్తిని అయనీకరణ శక్తి అని, ఈ ప్రక్రియను అయనీకరణం అంటారు.
2. పరమాణువు నుండి ఎలక్ట్రానన్ను తొలగించటానికి కావాల్సిన శక్తిని, త్వరణ పొటెన్షియల్ ఇస్తుంది. దీనినే అయనీకరణ పొటెన్షియల్ అంటారు.
3. ఉదాహరణకు హైడ్రోజన్ పరమాణువు భూస్థాయిలో ఉన్న ఎలక్ట్రాన్కు మొత్తం శక్తి + 13.6 eV కావాలి.
4. ఒక పరమాణువు అయనీకరణ పొటెన్షియల్ సాధారణ సమీకరణము V = \(\frac{13.6Z^2}{n^2}\) వోల్ట్.
   ఇక్కడ Z పరమాణు సంఖ్య మరియు n ఎలక్ట్రాన్ తొలగించబడిన కక్ష్య సంఖ్య.
5. ఇచ్చిన మూలకంనకు, అయనీకరణ పొటెన్షియల్ స్థిరం. వేర్వేరు మూలకాలు వేర్వేరు అయనీకరణ పొటెన్షియల్ విలువలు కలిగి ఉండును.

ప్రశ్న 8.
హైడ్రోజన్ పరమాణువులోని వివిధ రకాల వర్ణపట శ్రేణులను వివరించండి. [TS. Mar. 16; AP. Mar.’15]
జవాబు:
హైడ్రోజన్ పరమాణువు ఉద్గారించు రేఖ వర్ణపటం ఐదు శ్రేణులను కలిగి ఉండును.

ప్రశ్న 9.
క్వాంటీకరణను సూచించే బోర్ రెండవ ప్రతిపాదనకు డిబ్రాయ్ ఇచ్చిన వివరణపై లఘుటీకా వ్రాయండి. [TS. Mar ’17]
జవాబు:
బోర్ రెండవ క్వాంటీకరణ భావనకు డిబ్రాయ్ వివరణ :
1) బోర్ పరమాణు నమూన రెండవ భావన, కేంద్రకము చుట్టూ తిరగే ఎలక్ట్రాన్ కోణీయ ద్రవ్యవేగం క్వాంటీకరణం అవుతుందని చెబుతుంది.
i.e., mvr = \(\frac{nh}{2 \pi}\) ఇక్కడ n = 1, 2, 3, ….
2) డిబ్రాయ్ ప్రకారము, వృత్తాకార కక్ష్యలో ఉన్న ఎలక్ట్రాన్, బోర్ ప్రతిపాదించిన విధంగా, కణ తరంగముగా చూడవచ్చును.
3) రెండు వైపులా స్థిరంగా బిగించిన తీగను మీటితే, హెచ్చు తరంగదైర్ఘ్యాల సంఖ్య ఉన్న స్థావర తరంగం ఏర్పడును.
4) తీగలో స్థావర తరంగాలు ఏర్పడినపుడు, తరంగముపైకి మరియు క్రిందికి ప్రయాణించిన మొత్తం దూరము తరంగధైర్ఘ్యాల సంఖ్యకు పూర్ణ గుణిజాలుగా ఉండును.
5) డీబ్రాయ్ ప్రకారము, ఒక స్థావర కక్ష్య తిరిగే ఎలక్ట్రాన్తో డీబ్రోగ్లీ తరంగాల పూర్ణ సంఖ్యను కలిగి ఉండును.
6) ఒక ఎలక్ట్రాన్ r_n వ్యాసార్ధము ఉన్న గవ వృత్తాకార కక్ష్యలో భ్రమణం చెందితే, మొత్తం ప్రయాణించిన దూరము = కక్ష్య వృత్త పరిధి = 2πr_n
∴ అనుమతించబడిన కక్ష్యకు, 2πr_n = nλ

i.e., nవ కక్ష్యలో తిరిగే ఎలక్ట్రాన్ కోణీయ ద్రవ్యవేగము \(\frac{h}{2 \pi}\) పూర్ణ గుణజంనకు సమానం.
బోర్ ప్రతిపాదించిన రెండవ భావనకు ఇదియే షరతు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
α – కణాల పరిక్షేపణపై గైగర్-మార డెన్ల ప్రయోగాన్ని వర్ణించండి. ఈ ప్రయోగంలో కేంద్రక పరిమాణాన్ని ఎలా అంచనా వేస్తారు?
జవాబు:

1. రూథర్ ఫర్డ్ మరియు అతని సహోద్యోగులు, గైగర్ మరియు మారె డెన్ ప్రయోగ అమరిక పటంలో చూపబడింది.
2. సీసపు రంధ్రములోని రేడియోధార్మిక జనకం నుండి ఉద్గారమయ్యే – కణాలు, సీసపు చీలిక ద్వారా సన్నని పుంజంగా సమాంతీకరించబడతాయి.
   
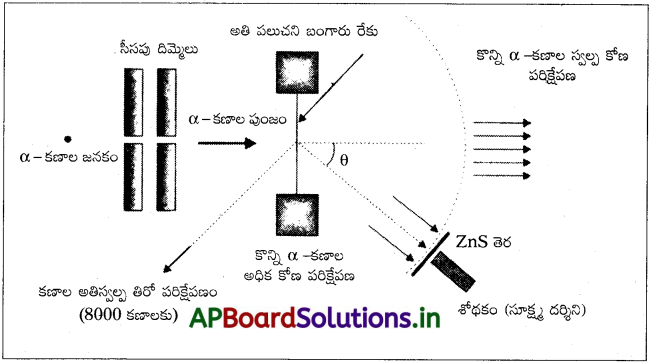
3. సమాంతరీకరణ పుంజము 2.1 × 10^-7m మందం ఉన్న పలుచని బంగారు రేకుపై పతనమవుతాయి.
4. వేర్వేరు దిశలలో పరిక్షేపణ α- కణాలను, జింక్ సల్ఫైడ్ తెర మరియు మైక్రోస్కోప్ కలిగి ఉన్న భ్రమణ శోధకం ద్వారా పరిశీలిస్తారు.
5. జింక్ సల్ఫైడ్ తెరపై వెలుగు మెరుపులు లేక ప్రస్ఫురణలను ఏర్పడతాయి.
6. పతన పుంజం దిశ నుండి వేర్వేరు కోణాల వద్ద మైక్రోస్కోప్ ద్వారా పరిశీలించి గణిస్తారు.
7. α –కణం, తొలిదశ నుండి విచలనకోణం θ ను పరిక్షేపణ కోణం θ అంటారు.

పరిశీలనలు:

1. బంగారు రేకు ద్వారా ఎక్కువ x-కణాలు సరళపథంలో చలిస్తాయి. α- కణాలు, బంగారు పరమాణువులతో అభిఘాతం పవు.
2. పతన α- కణాలలో 0.14% మాత్రమే 1° కన్నా ఎక్కువ పరిక్షేపణ చెందుతాయి.
3. 8000 α-కణాలలో, ఒక్క – కణం 90° కన్నా ఎక్కువ అపవర్తనం చెందును.

కేంద్రకం పరిమాణం నిర్ణయించుట:

1. రూథర్ఫర్డ్ భావన ప్రకారము, పరమాణువు మొత్తం ధనావేశం, పరమాణువు చిన్న కేంద్రక కోర్లో కేంద్రీకకరించబడును. ప్రతిపరమాణు చిన్న కేంద్రక కోర్ను, పరమాణు కేంద్రకం అంటారు.
2. గ్రహాలు, సూర్యుని చుట్టూ తిరుగుతున్నట్లే కేంద్రము చుట్టూ కక్ష్యలలో ఎలక్ట్రాన్లు చలిస్తాయి.
3. రూథర్ ఫర్డ్ ప్రయోగము, కేంద్రకం యొక్క పరిమాణం 10^-15 m నుండి 10^-14m ఉండునని తెలిపినవి. గతిజ సిద్ధాంతం నుండి పరమాణు పరిమాణం 10^-10m, సుమారుగా కేంద్రక పరిమాణంనకు 10,000 నుండి 1,00,000 రెట్లు ఎక్కువగా ఉండును.

ప్రశ్న 2.
హైడ్రోజన్ పరమాణువు వర్ణపటాన్ని వివరించే బోర్ సిద్ధాంతాన్ని చర్చించండి.
జవాబు:

1. బోర్ నమూన ప్రకారము, ఎలక్ట్రాన్ నిర్విరామంగా స్థిర కేంద్రకం చుట్టూ స్థావర కక్ష్యలలో భ్రమణం చెందును. దీనినే పరమాణు భూస్థాయి అంటారు. భూస్థాయి ఎటువంటి వికిరణాన్ని ఉద్గారించదు.
2. పరమాణువుకు కొంతశక్తిని ఇస్తే, ఆ శక్తిని ఎలక్ట్రాన్ శోషణం చేయును. దీనినే పరమాణువు ఉత్తేజిత స్థాయి అంటారు. ఈ స్థితిలో ఎలక్ట్రాన్ తరువాత హెచ్చు కక్ష్యలలోనికి దూకును. అక్కడ 10^-8 sec. మాత్రమే ఉండి, వెంటనే భూస్థాయికి వచ్చును. స్థాయిలలోని శక్తిభేదము వర్ణపట రేఖగా ఉద్గారమగును.
3. బోర్ మూడవ భావన ప్రకారము, ఉద్గారశక్తి E = hν = E₂ – E
   

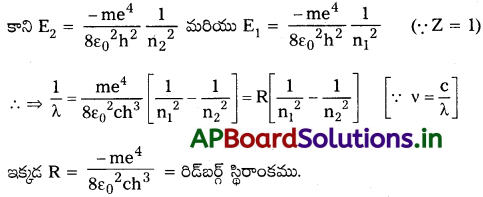
హైడ్రోజన్ పరమాణువు యొక్క వర్ణ పట శ్రేణి :

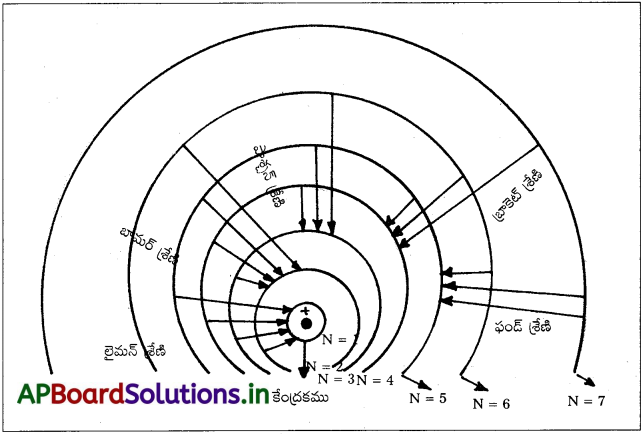
హైడ్రోజన్ పరమాణువు ఐదు శ్రేణుల వర్ణపట రేఖలను కలిగి ఉండును. అవి

1. లైమన్ శ్రేణి :
ఎలక్ట్రాన్ బాహ్యకక్ష్యల నుండి మొదటి కక్ష్యలోనికి దూకిన, అతినీల లోహిత ప్రాంతంలో వర్ణపట రేఖలు ఏర్పడును. ఇక్కడ n₁ = 1, n₂ = 2, 3, 4, 5…..

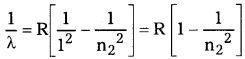
2) బామర్ శ్రేణి :
ఎలక్ట్రాన్ బాహ్యకక్ష్యల నుండి, రెండవ కక్ష్యలలోనికి దూకితే, దృశ్యా ప్రాంతంలో వర్ణపట రేఖలు ఏర్పడును. ఇక్కడ n₁ = 2, n₂ = 3, 4, 5…..

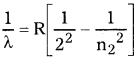
3) పాశ్చన్ శ్రేణి :
ఎలక్ట్రాన్ బాహ్యకక్ష్యల నుండి మూడవ కక్ష్యలోనికి దూకితే సమీప పరారుణ ప్రాంతంలో వర్ణపట రేఖలు ఏర్పడును. ఇక్కడ n₁ = 3, n₂ = 4, 5, 6 …..

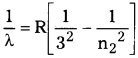
4) బ్రాకెట్ శ్రేణి :
ఎలక్ట్రాన్ బాహ్యకక్ష్యల నుండి నాల్గవ కక్ష్యలోనికి దూకితే, పరారుణ ప్రాంతంలో వర్ణపట రేఖలు ఏర్పడతాయి. ఇక్కడ n₁ = 4, n₂ = 5, 6, 7 ….

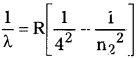
5) ఫండ్ శ్రేణి :
ఎలక్ట్రాన్ బాహ్యకక్ష్యల నుండి ఐదవ కక్ష్యలోనికి దూకితే, దూరపరారుణ ప్రాంతంలో వర్ణపట రేఖలు ఏర్పడును. ఇక్కడ n₁ = 5, n₂ = 6, 7, 8, …..

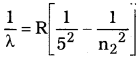
ప్రశ్న 3.
పరమాణు వర్ణపటాన్ని వివరించే బోర్ సిద్ధాంతం యొక్క ప్రతిపాదనలను (postulates) తెలపండి. వీటినుంచి హైడ్రోజన్, పరమాణువులో కక్ష్యా వ్యాసార్థానికి, కక్ష్యలోని ఎలక్ట్రాన్ శక్తికి సమీకరణాలను పొందండి. [AP. Mar.’16]
జవాబు:
a) బోర్ సిద్ధాంత భావనలు :
1) పరమాణువులో కేంద్రకం చుట్టూ ఎలక్ట్రాన్లు వేర్వేరు కక్ష్యలలో తిరుగుతాయి. వీటినే స్థావర కక్ష్యలు అంటారు. ఎలక్ట్రాన్లు వాని స్థావర స్థాయిలలో చలిస్తున్నప్పుడు వికిరణంను ఉద్గారించవు.

2) ఎలక్ట్రాన్ అనుమతించబడిన కక్ష్యలలో మాత్రమే తిరుగును. వాని కోణీయ ద్రవ్యవేగం \(\frac{h}{2 \pi}\) కు పూర్ణంక గుణిజంగా ఉండును.
i.e., mυ_nr_n = \(\frac{nh}{2 \pi}\) → (1)
ఇక్కడ n = 1, 2, 3…..

3) ఒక ఎలక్ట్రాన్ హెచ్చుశక్తి (E₂) కక్ష్య నుండి తక్కువ శక్తి (E₁) కక్ష్యలోనికి దూకితే, వాని శక్తుల భేదంనకు సమాన శక్తి గల వికిరణం ఉద్గారమగును.
i.e., E = hν = E2 – E ⇒ ν = \(\frac{E_2-E_1}{h}\) → (2)

b) ఉద్గార వికిరణం శక్తి :
హైడ్రోజన్ పరమాణువులో ఆ ఆవేశం ఉన్న ఒక ఎలక్ట్రాన్, e ఆవేశం ఉన్న కేంద్రకం చుట్టూ r_n వ్యాసార్థం ఉన్న వృత్తాకార కక్ష్యలో తిరుగుతుంది.

1) ఎలక్ట్రాన్ గతిజశక్తి :
ఎలక్ట్రాన్ వృత్తాకార కక్ష్యలో తిరుగుటకు, అభికేంద్ర బలం = ఎలక్ట్రాన్ మరియు కేంద్రకం మధ్య స్థిరవిద్యుదాకర్షణ బలం.

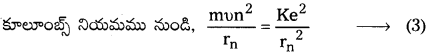
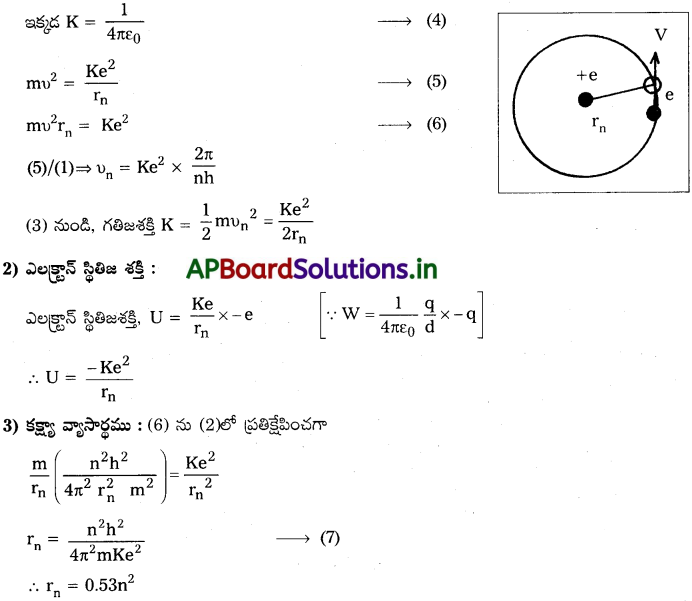
4) మొత్తం శక్తి (E_n) :
కేంద్రకం చుట్టూ తిరుగు ఎలక్ట్రాన్కు గతిజశక్తి మరియు స్థితిజశక్తి ఉండును.

అభ్యాసాలు Textual Exercises

ప్రశ్న 1.
ఒక హైడ్రోజన్ పరమాణువు మొదటి ఎలక్ట్రాన్ కక్ష్యావ్యాసార్థం 5.3 × 10^-11m. రెండవ కక్ష్య వ్యాసార్థం ఎంత?
సాధన:

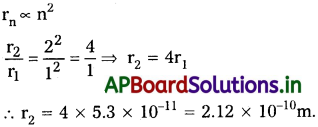
ప్రశ్న 2.
హైడ్రోజన్ పరమాణువు మొదటి కక్ష్య వ్యాసార్ధాన్ని కనుక్కోండి. మొదటి కక్ష్యలోని ఎలక్ట్రాన్ వేగం, పౌనఃపున్యాలు ఎంత ఉంటాయి?
దత్తాంశం: h = 6.62 × 10^-34 Js, m = 9.1 × 10^-31kg, e = 1.6 × 10^-19 C, k = 9 × 10⁹ m²C.
సాధన:
ఇచ్చినవి h = 6.62 × 10^-34 J-s,
m = 9.1 × 10^-31 kg
e = 1.6 × 10^-19C;
K = 9 × 10⁹ Nm²C^-2, n = 1

ప్రశ్న 3.
హైడ్రోజన్ పరమాణువులో మొదటి ఉత్తేజిత స్థాయిలోని ఎలక్ట్రాన్ మొత్తం శక్తి -3.4eV. ఈ స్థాయిలో ఎలక్ట్రాన్ స్థితిజశక్తి ఎంత?
సాధన:
మొదటి కక్ష్యలో, E = – 3.4 eV

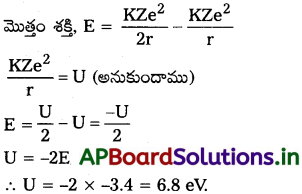
ప్రశ్న 4.
హైడ్రోజన్ పరమాణువులో మొదటి ఉత్తేజిత స్థాయిలోని ఎలక్ట్రాన్ మొత్తం శక్తి -3.4eV. ఈ స్థాయిలో ఎలక్ట్రాన్ గతిజశక్తి ఎంత?
సాధన:
హైడ్రోజన్ వంటి పరమాణువుకు,
K = – మొత్తం శక్తి అవుతుంది.
ఇక్కడ E = – 3.4eV
∴ K = – (-3.4) = 3.4 eV.

ప్రశ్న 5.
భూస్థాయిలో ఉన్న హైడ్రోజన్ పరమాణువు వ్యాసార్థాన్ని లెక్కించండి. n = 1 వ కక్ష్యలో ఎలక్ట్రాన్ వేగాన్ని కూడా
h = 6.63 × 10^-34Js, m = 9.1 × 10^-31 kg, e = 1.6 × 10^-19 C, K = 9 × 10⁹N m²C^-2.
సాధన:
n = 1, h = 6.63 × 10^-34 J-s,
m = 9.1 × 10^-31 kg
e = 1.6 × 10^-19C,
K = 9 × 10⁹ Nm²C^-2

ప్రశ్న 6.
హైడ్రోజన్ పరమాణువు అయనీకరణ శక్తి 13.6 eV అని చూపండి.
సాధన:
భూస్థాయికి, n = 1

హైడ్రోజన్ పరమాణువు, భూస్థాయి నుండి ఎలక్ట్రాన్ను స్వేచ్ఛగా ఉంచటానికి కావాల్సిన కనీస శక్తి = 13.6 eV,
∴ హైడ్రోజన్ పరమాణువు యొక్క అయనీకరణ శక్తి = 13.6 eV.

ప్రశ్న 7.
లిథియం పరమాణువు అయనీకరణ శక్తిని లెక్కించండి.
సాధన:
₃Li⁷ పరమాణువుకు, Z = 3, n = 2 [∵ Li=1s² 2s¹]

∴ లిథియం అయనీకరణ = 30.6eV.

ప్రశ్న 8.
లైమన్ శ్రేణిలోని మొదటి రేఖ (first member) తరంగదైర్ఘ్యం 1216 Å. బామర్ శ్రేణిలోని రెండవ రేఖ (second member) తరంగదైర్ఘ్యాన్ని లెక్కించండి.
సాధన:

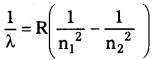
ప్రశ్న 9.
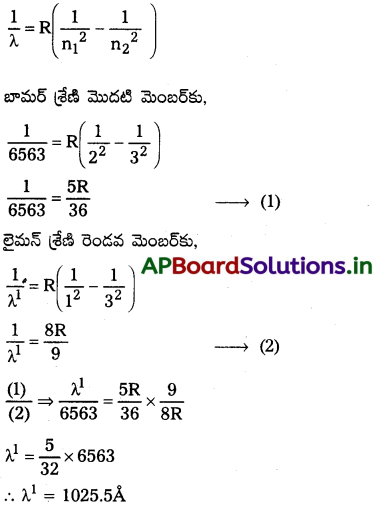
బామర్ శ్రేణిలోని మొదటి రేఖ తరంగదైర్ఘ్యం 6563 Å. లైమన్ శ్రేణిలోని రెండవ రేఖ తరంగదైర్ఘ్యాన్ని లెక్కించండి.
సాధన:

ప్రశ్న 10.
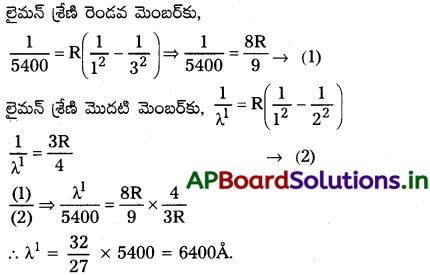
హైడ్రోజన్ వర్ణపటం లైమన్ శ్రేణిలోని రెండవరేఖ తరంగదైర్ఘ్యం 5400 Å. దీనిలోని మొదటిరేఖ తరంగదైర్ఘ్యాన్ని కనుక్కోండి.
సాధన:

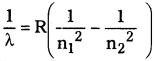
ప్రశ్న 11.
బామర్ శ్రేణిలోని హ్రస్వ తరంగదైర్ఘ్యాన్ని లెక్కించండి (లేదా) బామర్ శ్రేణి అవధి తరంగదైర్ఘ్యాన్ని లెక్కించండి.
R = 10970000m^-1.
సాధన:

ప్రశ్న 12.
రిడ్బర్గ్ ఫార్ములాను ఉపయోగించి, హైడ్రోజన్ పరమాణువు బామర్ శ్రేణిలోని మొదటి నాలుగు వర్ణపట రేఖల తరంగదైర్యాలను లెక్కించండి.
సాధన:

అదనపు అభ్యాసాలు Additional Exercises

ప్రశ్న 1.
ప్రతివాక్యం చివర ఇచ్చిన ఆధారాలను ఆసరాగా చేసుకొని సరైన ప్రత్యామ్నాయాన్ని ఎంచుకోండి :
a) థామ్సన్ నమూనాలో పరమాణు పరిమాణం, రూథర్ ఫర్డ్ నమూనాలోని పరమాణు పరిమాణం….. (కంటే చాలా ఎక్కువ / లలో తేడా ఏమి ఉండదు / కంటే చాలా తక్కువ).
b) ……. లో భూస్థాయిలోని ఎలక్ట్రాన్లు స్థిర సమతాస్థితి (stable equilibrium) లో ఉంటాయి. అయితే ………. లో ఎలక్ట్రాన్లు ఎప్పుడూ ఒక నికర బలాన్ని అనుభవిస్తాయి. (థామ్సన్ నమూనా / రూథర్ఫర్డ్ నమూనా).
c) ………… పై ఆధారపడిన ఒక సంప్రదాయక పరమాణువు అంతిమంగా కుప్పకూలిపోయి నశించాల్సిందే. (థామ్సన్ నమూనా / రూథర్ ఫర్డ్ నమూనా).
d) ……..లో ఒక పరమాణువు దాదాపు అవిచ్ఛిన్న ద్రవ్యరాశి వితరణను కలిగి ఉంటుంది. కాని …………… లోనైతే అత్యధిక అసమరీతి ద్రవ్య వితరణను కలిగి ఉంటుంది. (థామ్సన్ నమూనా / రూథర్ ఫర్డ్ నమూనా).
e) ……….. పరమాణువు ధనావేశిత భాగం మొత్తం ద్రవ్యరాశిలో అత్యధిక ద్రవ్యరాశిని కలిగి ఉంటుంది. (రూథర్ ఫర్డ్ నమూనాలో / రెండు నమూనాల్లోను).
జవాబు:
a) వేరే రూపంలో ఉండదు.
b) థామ్సన్ నమూనా, రూథర్ ఫర్డ్ నమూనా
c) రూథర్ ఫర్డ్ నమూనా
d) థామ్సన్ నమూనా, రూథర్ఫర్డ్ నమూనా
e) రెండు నమూనాలు

ప్రశ్న 2.
బంగారు రేకు స్థానంలో పలుచని ఘన హైడ్రోజన్ పలకను ఉపయోగించి ఆల్ఫా-కణ పరిక్షేపణ ప్రయోగాన్ని మరోసారి నిర్వహించడానికి, ఒకవేళ మీకొక అవకాశం ఇస్తే మీరు ఏయే ఫలితాలను ఆశిస్తారు? (14 K కంటే తక్కువ ఉష్ణోగ్రతల వద్ద హైడ్రోజన్ ఘనపదార్థ రూపంలో ఉంటుంది).
జవాబు:
బంగారు రేకు స్థానంలో ఘనహైడ్రోజన్ పలకను, . కణంను ప్రక్షేపకంగా ఉపయోగించి పరిక్షేపణ ప్రయోగంను మరల చేస్తే విజయం సాధించలేము. కారణం హైడ్రోజన్ చాలా తేలికైనది. స్థితిస్థాపక అభిఘాతంలో, అభిఘాతం తరువాత లక్ష్య హైడ్రోజన్, ఆల్ఫాతో పోల్చిన వేగంగా చలించును. కావున హైడ్రోజన్ కేంద్రకము పరిమాణాన్ని నిర్ధారించలేము.

ప్రశ్న 3.
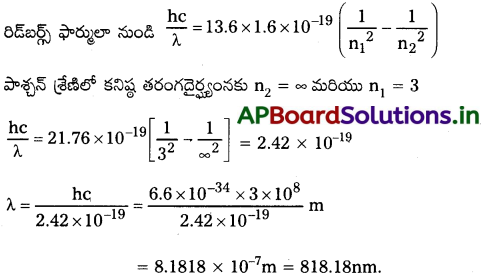
వర్ణపట రేఖల పాశ్చన్ శ్రేణిలో హ్రస్వ తరంగదైర్ఘ్యం ఎంత?
జవాబు:

ప్రశ్న 4.
ఒకానొక పరమాణువులో 2.3 eV భేదం రెండు శక్తిస్థాయిలను వేరుచేస్తుంది. ఆ పరమాణువు ఎగువ శక్తి స్థాయి నుంచి దిగువ శక్తి స్థాయికి సంక్రమణం చెందినప్పుడు ఉద్గారమయ్యే వికిరణం పౌనఃపున్యం ఎంత?
జవాబు:
E = 2.3eV = 2.3 × 1.6 × 10^-19 J
E = hν

ప్రశ్న 5.
హైడ్రోజన్ పరమాణువు భూస్థాయి శక్తి-13.6 eV. ఈ స్థాయిలో ఉన్న ఎలక్ట్రాన్ గతిజ, స్థితిజశక్తులు ఎంతెంత?
జవాబు:
మొత్తం శక్తి, E = – 13.6 eV
K.E = -E = 13.6 eV
P.E. = -2.K.E. = -2 × 13.6 = -27.2 eV.

ప్రశ్న 6.
తొలుత భూస్థాయిలో ఉన్న ఒక హైడ్రోజన్ పరమాణువు ఒక ఫోటాన్ ను శోషించుకొని, n = 4 స్థాయికి ఉత్తేజితం చెందింది. ఫోటాన్ తరంగదైర్ఘ్యం, పౌనఃపున్యాలను నిర్ధారించండి.
జవాబు:
భూస్థాయికి n₁ = 1 మరియు n₂ = 4
ఫోటాన్ శోషణ శక్తి E = E₂ – E₁

ప్రశ్న 7.
బోర్ నమూనాను ఉపయోగించి హైడ్రోజన్ పరమాణువు n = 1, 2, 3 స్థాయిలలో (a) ఎలక్ట్రాన్ వడిని లెక్కించండి. (b) ఇందులోని ప్రతిస్థాయిలో (ఎలక్ట్రాన్) కక్ష్య ఆవర్తన కాలాన్ని లెక్కగట్టండి.
జవాబు:

ప్రశ్న 8.
హైడ్రోజన్ పరమాణువులోని అత్యంత అంతర (innermost) ఎలక్ట్రాన్ కక్ష్యా వ్యాసార్ధం 5.3 × 10^-11 m అయితే n = 2, n = 3 కక్ష్యల వ్యాసార్థాలు ఎంతెంత?
జవాబు:
r_n = n²r
∴ r₂ = 4r₁ = 4 × 5.3 × 10^-11m = 2.12 × 10^-10m
r₃ = 9r₁ = 9 × 5.3 × 10^-11m = 4.77 × 10^-10m.

ప్రశ్న 9.
12.5 eV ఎలక్ట్రాన్ శక్తి పుంజాన్ని గది ఉష్ణోగ్రత వద్ద ఉన్న వాయు హైడ్రోజన్ ను తాడనం చేయడానికి ఉపయోగించారు. ఏయే తరంగదైర్ఘ్యాలు శ్రేణులు ఉదార్గమవుతాయి?
జవాబు:
భూస్థాయిలో, గది ఉష్ణోగ్రత వద్ద హైడ్రోజన్ వాయువు శక్తి -13.6 eV, 12.5 eV శక్తి ఉన్న ఎలక్ట్రాన్ పుంజం, హైడ్రోజన్తో ఢీకొన్నప్పుడు, శక్తి = – 13.6 + 12.5 = -1.1eV.
ఎలక్ట్రాన్ n = 1 నుండి n = 3కు దూకితే, E₃ = \(\frac{-13.6}{3^2}\) = -1.1eV

ఎలక్ట్రాన్ n = 3 నుండి n = 2 కు దూకి, బామర్ శ్రేణిని ఇస్తుంది. ఎలక్ట్రాన్ n = 3 నుండి n = 1 కి దూకి, లైమన్ శ్రేణిని ఇస్తుంది.

ప్రశ్న 10.
1.5 × 10¹¹ m వ్యాసార్ధం ఉన్న కక్ష్యలో 3 × 10⁴ m/s కక్ష్యా వడిలో సూర్యుడి చుట్టూ తిరుగుతున్న భూమి పరిభ్రమణాన్ని అభిలక్షణీకరించే క్వాంటం సంఖ్యను బోర్ నమూనాకు అనుగుణంగా లెక్కించండి.
(భూమి ద్రవ్యరాశి = 6.0 × 10²⁴ kg.)
జవాబు:
r = 1.5 × 10¹¹m, v = 3 × 10⁴m/s, m = 6.0 × 10²⁴kg

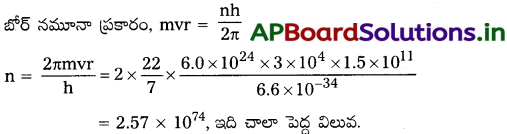
ప్రశ్న 11.
థామ్సన్ నమూనా, రూథర్ఫర్డ్ నమూనాల మధ్య భేదాన్ని మీరు బాగా అర్ధం చేసుకోవడంలో తోడ్పడే క్రింది ప్రశ్నలకు సమాధానాలను ఇవ్వండి.
a) α – కణాలు పలుచని బంగారు రేకుపై పడి అపవర్తనం చెందే ప్రయోగంలో, థామ్సన్ నమూనా ఆధారంగా ప్రాగుక్తం చేసిన α – కణ సరాసరి అపవర్తన కోణం, రూథర్ ఫర్డ్ నమూనా ఆధారంగా అంచనా వేసిన సరాసరి అపవర్తన కోణం కంటే తక్కువా? దాదాపు సమానమా? ఎక్కువా?
b) థామ్సన్ నమూనా ప్రాగుక్తం చేసిన తిరోగామి పరిక్షేపణ (అంటే, 90° కంటే ఎక్కువ కోణాలతో α-కణాల పరిక్షేపణం) సంభావ్యత రూథర్ ఫర్డ్ నమూనా ఆధారంగా ప్రాగుక్తం చేసిన తిరోగామి పరిక్షేపణ సంభావ్యత కంటే చాలా తక్కువగా ఉంటుందా? దాదాపు సమానంగా ఉంటుందా? లేదా చాలా ఎక్కువగా ఉంటుందా?
c) మిగతా ఇతర కారకాలను స్థిరంగా ఉంచినప్పుడు, ఒక స్వల్ప మందం t కి మధ్యస్థ కోణాల వద్ద పరిక్షేపణ అయ్యే α – కణాల సంఖ్య కి అనులోమానుపాతంలో ఉంటుందని ప్రయోగపూర్వకంగా కనుక్కొన్నారు. ఇదిలా పై రేఖీయంగా ఆధారపడి ఉండటం దేనిని సూచిస్తుంది?
d) ఒక పలుచని రేకుతో α-కణాలు పరిక్షేపణం చెందిన సందర్భంలో వాటి సరాసరి పరిక్షేపణ కోణాన్ని లెక్కించడం కోసం ఏ నమూనాలో బహుళ పరిక్షేపణాన్ని నిర్లక్ష్యం చేయడం పూర్తిగా తప్పవుతుంది?
జవాబు:
a) దాదాపు సమానం.
b) చాలా తక్కువగా ఉంటుంది. కారణం రూథర్ ఫర్డ్ నమూనా వలె, థామ్సన్ నమూనాలో కేంద్రకంలో కేంద్ర కోర్లో ద్రవ్యం ఉండదు.
c) a- కణాలు అధిక పరిక్షేపణను వివరించును.
d) థామ్సన్ ప్రయోగంలో,

ప్రశ్న 12.
హైడ్రోజన్ పరమాణువులోని ఎలక్ట్రాన్, ప్రోటాన్ల మధ్య ఉండే గురుత్వాకర్షణ బలం, వాటి మధ్య ఉండే కూలుమ్ – ఆకర్షణ బలం కంటే సుమారు 10⁴⁰ కారకంతో బలహీనంగా ఉంటుంది. ఈ వాస్తవాన్ని మరోవిధంగా పరిశీలించడం అంటే, హైడ్రోజన్ పరమాణువులోని ఎలక్ట్రాన్, ప్రోటానులు గురుత్వాకర్షణ వల్ల బద్ధమైనట్లయితే (bound) అప్పుడా పరమాణువు బోర్ మొదటి కక్ష్య వ్యాసార్థాన్ని అంచనా వేయడమే. లభించే సమాధానం మీకు ఆసక్తి గొలుపుతుంది.
జవాబు:

ఈ విలువ అంచనా వేసిన మొత్తం విశ్వం పరిమాణం కన్నా చాలా ఎక్కువ.

ప్రశ్న 13.
ఒక హైడ్రోజన్ పరమాణువు n స్థాయి నుంచి (1 – 1) స్థాయికి అనుత్తేజితం (de-excites) చెందినప్పుడు ఉద్గారమయ్యే వికిరణ పౌనఃపున్యానికి సమాసాన్ని పొందండి. అత్యధిక n విలువలకు, ఈ పౌనఃపున్యం, ఆ కక్ష్యలో తిరుగుతున్న ఎలక్ట్రాన్ సంప్రదాయక పరిభ్రమణ పౌనఃపున్యానికి సమానంగా ఉంటుందని చూపండి.
జవాబు:
హైడ్రోజన్ పరమాణువు n నుండి (n – 1) స్థాయికి వచ్చినప్పుడు పౌనఃపున్యం ఉన్న ఉద్గార వికిరణ శక్తి E = hν = E₂ – E₁.



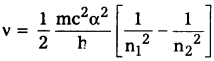
ఇది (i) ను పోలి ఉన్నది.
n హెచ్చు విలువలకు, n వ కక్ష్యలో ఎలక్ట్రాన్ సాంప్రదాయక భ్రమణ పౌనఃపున్యం, హైడ్రోజన్ పరమాణువు n నుండి (n – 1) స్థాయికి ఉద్గారమయినపుడు వికిరణ పౌనఃపున్యమునకు సమానము.

ప్రశ్న 14.
ఒక పరమాణువు కేంద్రకం చుట్టూ తిరిగే ఎలక్ట్రాన్, సంప్రదాయకంగా చూస్తే కేంద్రకం చుట్టూ ఉన్న ఏ కక్ష్యలలో అయినా ఉండవచ్చు. అలాంటప్పుడు పరమాణు విలక్షణ పరిమాణాన్ని ఏది నిర్ణయిస్తుంది ? ఒక పరమాణువు దాని విలక్షణ పరిమాణం కంటే, మనం మాటవరసకు అనుకోవడానికైనా, వెయ్యిరెట్లు ఎందుకు పెద్దదిగా ఉండదు? మీరీ పుస్తకంలో నేర్చుకొన్న ప్రఖ్యాతమైన పరమాణు నమూనాను బోర్ రూపొదించకముందు అతడిని బాగా కలవరపెట్టిన ప్రశ్న ఇది. బోర్, తన ఆవిష్కరణకు ముందు ఏమిచేసి ఉంటాడో దాన్ని మనం అనుకరించడానికి, ప్రకృతి యొక్క ప్రాథమిక స్థిరాంకాలతో కింద వివరించినట్లుగా వినోదిస్తూ, మనకు ఇంతకు ముందే తెలిసిన పరమాణు పరిమాణానికి (~ 10¹⁰m) దాదాపు సమానంగా ఉంటూ పొడవు మితులు కలిగినటువంటి భౌతిక రాశిని మనమేమైనా పొందగలమో లేదో చూద్దాం.
a) e, m, c అనే ప్రాథమిక స్థిరాంకాల నుంచి, పొడవు మితులు కలిగి ఉండే రాశిని నిర్మించండి. దాని సంఖ్యాత్మక విలువను నిర్ధారించండి.
b) పరమాణువు కొలతల పరిమాణ క్రమంతో పోల్చి చూస్తే, (a) నుంచి పొందిన పొడవు విలువ చాలా చాలా స్వల్పంగా ఉంటుందని మీరు తెలుసుకొంటారు. అంతేగాక, ఇందులో c మిళితమై ఉంటుంది. కాని ఎక్కడైతే పోషించే పాత్ర అంటూ ఏమీ ఉండదని భావిస్తామో, అలాంటి నిరపేక్షక్షేత్ర (non-relativistic domain) పరిధిలోనే పరమాణువుల శక్తి విలువలు అత్యధికంగా ఉంటాయి. సరియైన పరమాణు పరిమాణాన్ని పొందే ప్రయత్నంలో బహుశా ఈ తర్కమే c ని వదిలివేసి, ‘మరేదో ఇతర రాశి’పై దృష్టిసారించడానికి బోర్ను పులికొల్పి ఉంటుంది. ఈ విధంగా ఆలోచిస్తున్న సమయంలోనే అంతకు ముందుగానే ఏదో ఒకచోట ఉన్న ప్లాంక్ స్థిరాంకం h తెరముందుకు వచ్చింది. h, m_e, e అనే రాశులు పరమాణువు యొక్క సరియైన పరిమాణాన్ని అందిపుచ్చుకోవడంలో ఉపకరిస్తాయని బోర్ గుర్తించడంలోనే అతడి సునిశిత దృష్టి దాగి ఉంది. h, m_e, ఆ రాశుల నుంచి పొడవు మితి కలిగిన ఒక రాశిని రూపకల్పన చేయండి. అంతేగాక, దాని సంఖ్యాత్మక విలువ వాస్తవానికి సరైన పరిమాణ క్రమంలోనే ఉందని నిర్ధారించండి.
జవాబు:
a) ప్రాథమిక స్థిరాంకాలు e, m_e మరియు c లను ఉపయోగించి, పొడవు మితి గల రాశిని నిర్మించవచ్చు. ఈ రాశి

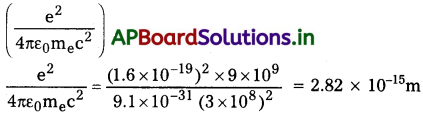
ఇది విలక్షణ పరమాణు పరిమాణం కన్నా చాలా తక్కువ.

b) c ను వదిలేసి hc, m_e మరియు ఆ లను ఉపయోగించి ఒక రాశిని నిర్మించుటకు, అది పొడవు మితులను కలిగి

ఇది పరమాణువు పరిమాణంనకు సమానం.

ప్రశ్న 15.
హైడ్రోజన్ పరమాణువులోని మొదటి ఉత్తేజిత స్థాయిలోని ఎలక్ట్రాన్ మొత్తం శక్తి దాదాపు 3.4 eV ఉంటుంది.
a) ఈ స్థాయిలోని ఎలక్ట్రాన్ గతిజశక్తి ఎంత?
b) ఈ స్థాయిలోని ఎలక్ట్రాన్ స్థితిజశక్తి ఎంత?
c) స్థితిజశక్తి శూన్య విలువను వేరేవిధంగా ఎంపిక చేసుకొంటే పై సమాధానాల్లోని ఏ సమాధానం మారిపోతుంది?
జవాబు:

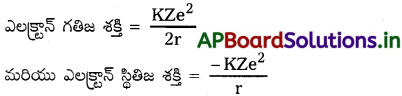
స్థితిజ శక్తి = -2 (గతిజశక్తి).
ఈ గణనలో, విద్యుత్ పొటెన్షియల్ మరియు స్థితిజశక్తి అనంత దూరం వద్ద శూన్యం.
మొత్తం శక్తి = PE + KE = 2KE + KE = -KE

a) మొదటి ఉత్తేజిత స్థాయిలో, మొత్తం శక్తి = -3.4 eV
∴K.E = – (-3.4eV) = + 3.4 eV.

b) మొదటి ఉత్తేజిత స్థాయిలో, ఎలక్ట్రాన్ స్థితిజశక్తి = -2KE = -2 × 3.4 = -6.8 eV.

c) శూన్య స్థితిజశక్తి మారితే, గతిజ శక్తి మారదు. KE విలువ + 3.4 eV ఉండును. ఏమైనప్పటికి శూన్యస్థితిజ శక్తి ఎన్నికతో PE. మరియు మొత్తం శక్తి మారవచ్చును.

ప్రశ్న 16.
బోర్ క్వాంటీకరణ ప్రతిపాదన (కోణీయ వేగం = nh/2π) అనేది ప్రకృతి యొక్క ఒక ప్రాథమిక నియమం అయినట్లయితే, అది గ్రహచలనాల సందర్భంలో కూడా అదేవిధంగా చెల్లుబాటు అయ్యితీరాలి. మరి అలాంటప్పుడు, సూర్యుని చుట్టూ తిరిగే గ్రహకక్ష్యల క్వాంటీకరణ గురించి మనమెప్పుడూ ఎందుకు మాట్లాడం?
జవాబు:
బోర్ క్వాంటీకరణ ప్రతిపాదన, ప్లాంక్ స్థిరాంకము h పదములో ఉండును. కాని భూగ్రహం కోణీయ ద్రవ్యవేగం = 10⁷⁰ h. బోర్ క్వాంటీకరణ ప్రతిపాదన పదములలో, ఇది 10⁷ కు అనురూపంగా ఉండును. n హెచ్చు విలువలకు, వరుస శక్తులు మరియు కోణీయ ద్రవ్యవేగ క్వాంటీకరణ శక్తుల మధ్య భేదము చాలా స్వల్పము. కావున స్థాయిలు అవిచ్ఛిన్నం మరియు విముక్తం కాదు.

ప్రశ్న 17.
ఒక మ్యూయానిక్ హైడ్రోజన్ పరమాణువు (munotic hydrogen atom) [సుమారు 207 m_e ద్రవ్యరాశి, రుణ విద్యుదావేశం కలిగి, ప్రోటాన్ చుట్టూ ఒక కక్ష్యలో తిరిగే జ్యుయాన్ (µ^–) కలిగి ఉండే ఒకానొక పరమాణువు] బోర్ మొదటి కక్ష్యా వ్యాసార్థాన్ని, భూస్థాయి శక్తినీ కనుక్కోండి.
జవాబు:
మ్యూనిక్ హైడ్రోజన్ ఒక పరమాణువు. దీనిలో ప్రోటాన్ వెంట 207 m_e ద్రవ్యరాశి, రుణావేశ మ్యూయాన్ పరిభ్రమించును.

సాధించిన సమస్యలు Textual Examples

ప్రశ్న 1.
రూథర్ ఫర్డ్ పరమాణు కేంద్రక నమూనాలో కేంద్రకం (వ్యాసార్థం సుమారు 10^-15 m) సౌరమండల నమూనాలోని సూర్యుడితో సాదృశ్యంగా ఉంటుంది. కేంద్రకం చుట్టూ ఒక నిర్దిష్ఠ కక్ష్యలో (వ్యాసార్థం ≈ 10^-10 m) తిరిగే ఎలక్ట్రాన్ ను సూర్యుడి చుట్టూ ఒక నిర్దిష్ట కక్ష్యలో తిరిగే భూమితో సరిపోల్చుకోవచ్చు. ఒకవేళ, సౌరవ్యవస్థ కొలతలు, పరమాణువు కొలతలు ఒకే అనుపాతంలో ఉన్నాయనుకొంటే, భూమి సూర్యునికి ఇప్పుడు వాస్తవంగా ఉన్న దూరం కంటే తక్కువ దూరంలో ఉంటుందా ? ఎక్కువ దూరంలో ఉంటుందా? భూకక్ష్య వ్యాసార్థం సుమారు 1.5 × 10¹¹m, సూర్యుని వ్యాసార్థాన్ని 7 × 10⁸ m గా తీసుకోవడమైంది.
సాధన:
ఎలక్ట్రాన్ కక్ష్యావ్యాసార్థం, కేంద్రక వ్యాసార్థానికి మధ్యనిష్పత్తి (10^-10 m) / (10^-15 m) = 10⁵, అంటే, ఎలక్ట్రాన్ కక్ష్యా వ్యాసార్థం, కేంద్రక వ్యాసార్థం కంటే 10⁵ రెట్లు ఎక్కువ. ఒకవేళ, సూర్యుని చుట్టూ ఉండే భూకక్ష్యా వ్యాసార్థం, సూర్యుని వ్యాసార్థం కంటే 10⁵ రెట్లు అధికంగా ఉండి ఉంటే, భూకక్ష్యా వ్యాసార్థం 10⁵ × 7 × 10⁸ m = 7 × 10¹³ m గా లెక్కతేలుతుంది. ఈ విలువ భూకక్ష్యా వ్యాసార్థం వాస్తవమైన విలువ కంటే 100 రెట్ల కంటే ఎక్కువ. కాబట్టి ఈ సందర్భంలో భూమి, సూర్యునికి మునుపటికంటే చాలా ఎక్కువ దూరంలో ఉంటుంది.

ఈ ఉదాహరణ వల్ల అర్థమయ్యేదేమిటంటే, మన సౌరవ్యవస్థలో ఉండే ఖాళీ ప్రదేశం కంటే చాలా ఎక్కువ భాగం ఖాళీ ప్రదేశాన్ని పరమాణువు కలిగి ఉంటుంది.

ప్రశ్న 2.
గైగర్-మార్సడెన్ ప్రయోగంలో, 7.7 MeV శక్తి గల α – కణం కేంద్రకాన్ని సమీపిస్తూ క్షణికంగా ఆగి వెనకకు మరలినట్లయితే, కేంద్రకానికి, α-కణానికి మధ్య ఉండే అత్యంత సామీప్య దూరం ఎంత?
సాధన:
ఇక్కడ, కీలకమైన భావన ఏమిటంటే α – కణం, బంగారపు కేంద్రకాలతో కూడిన వ్యవస్థ యొక్క మొత్తం యాంత్రిక శక్తి పరిక్షేపణ ప్రక్రియ అంతా నిత్యత్వమవుతుంది. α – కణం, కేంద్రకాల మధ్య అన్యోన్య చర్య జరగక ముందు వ్యవస్థ తొలి యాంత్రిక శక్తి E_i అనీ, α–కణం క్షణికంగా ఆగినప్పుడు ఆ వ్యవస్థ తుది యాంత్రిక శక్తి E_f అని అనుకొందాం. తొలిశక్తి E_i కేంద్రకంవైపు వస్తున్న α-కణం యొక్క గతిజశక్తి K, తుది గతిజశక్తి E_f వ్యవస్థ విద్యుత్ పొటెన్షియల్ శక్తి U. ఈ పొటెన్షియల్ శక్తి U ని, సమీకరణం నుంచి లెక్కించవచ్చు. α-కణం విరామ స్థానం వద్ద ఉన్నప్పుడు α – కణం కేంద్రం, బంగారపు కేంద్రకం మధ్యగల దూరం అనుకొందాం. అప్పుడు మనం, శక్తి నిత్యత్వం E_i = E_f ఈవిధంగా రాయవచ్చు.

ప్రకృతిసిద్ధ జనకం నుంచి ఉత్పత్తి అయిన α-కణాలు గరిష్ఠ గతిజశక్తి 7.7 MeV లేదా 1.2 × 10^-12 J గా లెక్క తేలింది. 1/4πε₀ = 9.0 × 10⁹Nm²/C² కాబట్టి, e = 1.6 × 10^-19 C గా తీసుకొంటే,

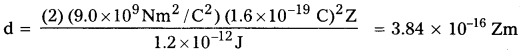
లోహపు రేకు బంగారంది కాబట్టి, బంగారు (Au) పరమాణు సంఖ్య Z = 79
d(Au) = 3.0 × 10^-14m = 30 fm. (1 fm (అంటే ఫెర్మి) = 10^-15m.)
కాబట్టి, బంగారపు కేంద్రకం వ్యాసార్థం 3.0 × 10^-14 m కంటే తక్కువ. బంగారపు కేంద్రక వ్యాసార్థం వాస్తవ విలువ 6 fm కాబట్టి, ఈ విలువకు పరిశీలించిన విలువకు అంత బాగా పొత్తు కుదరడం లేదు. ఈ విధమైన అసంగత్వానికి కారణం ఏమంటే, α-కణ వ్యాసార్థం, బంగారపు కేంద్రకం వ్యాసార్థాల మొత్తం కంటే, అత్యంత సామీప్య దూరం చాలా ఎక్కువ. కాబట్టి, α–కణం, బంగారపు కేంద్రకాన్ని నిజానికి స్పృశించకుండానే వెనకకు మరలి వెళ్తుంది.

ప్రశ్న 3.
ఒక హైడ్రోజన్ పరమాణువును ప్రోటాన్ , ఎలక్ట్రాన్ గా విడగొట్టడానికి 13.6 eV శక్తి అవసరమవుతుందని ప్రయోగం ద్వారా తెలిసింది. హైడ్రోజన్ పరమాణువులోని ఎలక్ట్రాన్ కక్ష్యా వ్యాసార్థాన్ని, వేగాన్ని లెక్కించండి.
సాధన:
హైడ్రోజన్ పరమాణువులోని ఎలక్ట్రాన్ మొత్తం శక్తి – 13.6 eV = – 13.6 × 1.6 × 10^-19J = – 2.2 × 10^-18 J.

ప్రశ్న 4.
సంప్రదాయక విద్యుదయస్కాంత సిద్ధాంతం ప్రకారం, హైడ్రోజన్ పరమాణువులోని ప్రోటాన్ చుట్టూ పరిభ్రమిస్తున్న ఎలక్ట్రాన్ ఉద్గారించే కాంతి తొలి పౌనఃపున్యాన్ని లెక్కగట్టండి.
సాధన:
హైడ్రోజన్ పరమాణువులో ప్రోటాన్ చుట్టూ 5.3 × 10^-11 h m వ్యాసార్థం ఉన్న కక్ష్యలో తిరిగే ఎలక్ట్రాన్ వేగం 2.2 × 10^-6 m/s అని పైన ఉదాహరణ నుంచి మనకు తెలుసు. కాబట్టి, ప్రోటాన్ చుట్టూ తిరుగుతున్న ఎలక్ట్రాన్ పౌనః పున్యం

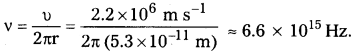
సంప్రదాయక విద్యుదయస్కాంత సిద్ధాంతం ప్రకారం, కేంద్రకం చుట్టూ పరిభ్రమిస్తున్న ఎలక్ట్రాన్ల లు ఉద్గారించే విద్యుదయస్కాంత తరంగాల పౌనఃపున్యం, కేంద్రకం చుట్టూ దాని పరిభ్రమణ పౌనఃపున్యానికి సమానం అని మనకు తెలుసు. కాబట్టి, ఉద్గారకాంతి తొలి పౌనఃపున్యం కూడా 6.6 × 10¹⁵ Hz అవుతుంది.

ప్రశ్న 5.
10 kg ల ఒక కృత్రిమ ఉపగ్రహం 8000 km వ్యాసార్థంగల ఒక కక్ష్యలో భూమి చుట్టూ ప్రతి 2 గంటలకొకసారి చుట్టి వస్తుంది. హైడ్రోజన్ పరమాణువులోని ఎలక్ట్రాన్లు వర్తించినట్లుగానే బోర్ కోణీయ ద్రవ్యవేగ ప్రతిపాదన ఈ కృత్రిమ ఉపగ్రహానికి కూడా వర్తిస్తుందని మనం ఊహిస్తే ఈ కృతిమ ఉపగ్రహం కక్ష్య యొక్క క్వాంటం సంఖ్యను కనుక్కోండి.
సాధన:
mυ_nr_n = nh/2π

ఇక్కడ m = 10 kg and r_n = 8 × 10⁶m. వృత్తాకారంగా తిరుగుతున్న ఉపగ్రహం ఆవర్తన కాలం T = 2h అంటే,
T = 7200 s. కాబట్టి, వేగం υ_n = 2πr_n/T.
కృత్రిమ ఉపగ్రహ కక్ష్య యొక్క క్వాంటం సంఖ్య n = (2πr_n)² × m(T × h)
ఆయా విలువలను ప్రతిక్షేపించగా,
n = (2π × 8 × 10⁶m)² × 10/(7200 s × 6.64 × 10^-34 Js) = 5.3 × 10⁴⁵

ఇక్కడ గమనించాల్సిన విషయం ఏమిటంటే, కృత్రిమ ఉపగ్రహ చలనం సందర్భంలోని క్వాంటం సంఖ్య చాలా చాలా ఎక్కువ ! నిజానికి ఇటువంటి అతిపెద్ద క్వాంటం సంఖ్యల సందర్భంలో క్వాంటీకరణ నిబంధన మూలంగా లభించే ఫలితాలు, సంప్రదాయక భౌతికశాస్త్ర ఫలితాలకు దగ్గరగా ఉంటాయి.

ప్రశ్న 6.
రిడ్ బర్గ్ ఫార్ములాను ఉపయోగించి, హైడ్రోజన్ వర్ణపటం లైమన్ శ్రేణిలోని మొదటి నాలుగు వర్ణపట రేఖల తరంగదైర్ఘ్యాలను లెక్కించండి.
సాధన:
రిడ్ బర్గ్ ఫార్ములా