Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 14th Lesson Nuclei Textbook Questions and Answers.
AP Inter 2nd Year Physics Study Material 14th Lesson Nuclei
Very Short Answer Questions
Question 1.
What are isotopes and isobars?
Answer:
Isotopes: The nuclei having the same atomic number (Z) but different mass numbers (A) are called isotopes.
E.g.:
\({ }_8^{16} \mathrm{O}\), \({ }_8^{17} \mathrm{O}\), \({ }_8^{18} \mathrm{O}\)
Isobars: The nuclei having the same neutron number (N) but different atomic number (Z) are called isobars.
E.g.: \({ }_6^{14} \mathrm{C}\), \({ }_7^{14} \mathrm{N}\)
Question 2.
What are isotones, and isomers?
Answer:
Isotones : The nuclei having same neutron number (N) but different atomic numbers (Z) are called isotones.
E.g. : \({ }_80^{198} \mathrm{Hg}\), \({ }_79^{197} \mathrm{N}\)
Isomers: Nuclei having the same atomic number (Z) and mass number (A) but with different nuclear properties such as radioactive decay and magnetic moments are called isomers.
E.g. : \({ }_{35}^{80} \mathrm{Br}^{\mathrm{m}}\), \({ }_{35}^{80} \mathrm{Br}^{\mathrm{g}}\)
![]()
Question 3.
What is a.m.u. ? What is its equivalent energy ?
Answer:
The mass of \(\frac{1}{12}\)th of the mass of \({ }_6^{12} \mathrm{C}\) atom is called atomic mass unit (a.m.u)
1 a.m.u = \(\frac{1}{12}\) of mass of \({ }_6^{12} \mathrm{C}\) atom = 1.66 × 10-27 kg
Equivalent energy of a.m.u= 931.5 MeV
Question 4.
What will be the ratio of the radii of two nuclei of mass numbers A1 and A2 ?
Answer:
The ratio of the radii of two nuclei of mass numbers A1 and A2 will be \(\frac{R_1}{R_2}\) = \(\left[\frac{\mathrm{A}_1}{\mathrm{~A}_2}\right]^{\frac{1}{3}}\) since R = R0 A1/3.
Question 5.
Natural radioactive nuclei are mostly nuclei of high mass number why ?
Answer:
Natural radioactivity is displayed by heavy nuclei beyond lead in the periodic table because of relatively low binding energy per nucleon as 7.6 MeV Hence to attain greater stability.
Question 6.
Does the ratio of neutrons to protons in a nucleus increase, decrease or remain the same after the emission of an α – particle ?
Answer:
The ratio of neutrons to protons in a nucleus, increases after the emission of an α – particle.
E.g. : Taking,
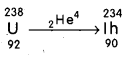
Before emission, the ratio of neutrons to protons
= \(\frac{\mathrm{A}-\mathrm{Z}}{\mathrm{Z}}\) = \(\frac{238-92}{92}\) = \(\frac{144}{92}\) = 1.57
After emission, the ratio of neutrons to protons
= \(\frac{234-90}{90}\) = 1.6
Question 7.
A nucleus contains no electrons but can emit them. How?
Answer:
When the nucleus disintegrates and radiates β-rays, it is said to be β-decay. β-particles are nothing but electrons. So the nucleus eject electrons.
![]()
Question 8.
What are the units and dimensions of the disintegration constant ?
Answer:
λ = –\(\frac{0.693}{\mathrm{~T}}\)
Units = sec-1
Dimensions = -1
Question 9.
Why do all electrons emitted during β-decay not have the same energy ?
Answer:
When a neutron is converted into a proton, an electron and neutron are emitted along with it
![]()
In β – decay proton remains in the nucleus, but electron and neutron are emitted with constant energy. The energy of neutron is not constant. So, all electrons do not have same energy.
Question 10.
Neutrons are the best projectiles to produce nuclear reactions. Why ?
Answer:
Neutrons are uncharged particles. So they do not deflected by the electric and magnetic fields. Hence Neutrons are considered as best projectiles in nuclear reaction.
Question 11.
Neutrons cannot produce ionization. Why ?
Answer:
Because neutrons are uncharged particles and cannot produce ionization.
Question 12.
What are delayed neutrons ?
Answer:
Neutrons are emitted in the fission products after sometime are called delayed neutrons.
Question 13.
What are thermal neutrons ? What is their importance ?
Answer:
Neutrons having kinetic energies approximately 0.025 eV are called as slow neutrons or thermal neutrons. 235U undergoes fission only when bombarded with thermal neutrons.
Question 14.
What is the value of neutron multiplication factor in a controlled reaction and in an uncontrolled chain reaction ?
Answer:
In controlled chain reaction K = 1
In uncontrolled chain reaction K > 1
Question 15.
What is the role of controlling rods in a nuclear reactor ?
Answer:
In nuclear reactor controlling rods are used to absorb the neutrons. Cadmium, boron materials are used in the form of rods in reactor. These control the fission rate.
Question 16.
Why are nuclear fusion reactions called thermo nuclear reactions ?
Answer:
Nuclear fusion occurs at very high temperatures. So it is called as thermo nuclear reaction.
Question 17.
Define Becquerel and Curie.
Answer:
Becquerel: 1 disintegration or decay per second is called Becquerel. It is SI unit of activity.
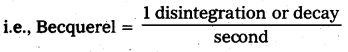
Curie : 3.7 × 1010 decays per second is called Curie.
1 Curie = 1Ci = \(\frac{3.7 \times 10^{10} \text { decays }}{\text { second }}\) = 3.7 × 1010 Bq.
Question 18.
What is a chain reaction ?
Answer:
Chain reaction: The neutrons produced in the fission of a nucleus can cause fission in other neighbouring nuclei producing more and more neutrons to continue the fission until the whole fissionable material is disintegrated. This is called chain reaction.
Question 19.
What is the function of moderator in a nuclear reactor ?
Answer:
They are used to slow down the fast moving neutrons produced during the fission process.
e.g.: Heavy water, Berilium.
![]()
Question 20.
What is the energy released in the fusion of four protons to form a helium nucleus ?
Answer:
26.7 MeV energy is released.
Short Answer Questions
Question 1.
Why is the density of the nucleus more than that of the atom ? Show that the density of nuclear matter is same for all nuclei.
Answer:
- Volume of the atom is greater than that of nucleus and it consists of nucleons
- Since density ∝ \(\frac{1}{\text { volume }}\)
∴ Density of the nucleus more than that of the atom. - Mass of the nucleus = no.of nucleons (A) × mass of nucleon (m)
= Am - Volume of the nucleus V= \(\frac{4}{3} \pi \mathrm{R}^3\)
= \(\frac{4}{3} \pi\left(R_0 A^{1 / 3}\right)^3\)
= \(\frac{4 \pi \mathrm{R}_0^3 \mathrm{~A}}{3}\) = 1.2 × 10-45m3.A. [∵ R0 = 1.2 × 10-15m]
i. e., the volume of the nucleus is proportional to the mass number A. - Density of the nucleus (ρ)

- The above equation represents it clear that the density of the nucleus is independent of the mass number A and is same for all the nuclei.
Question 2.
Write a short note on the discovery of neutron.
Answer:
- Bothe and Becker found that when beryllium is bombarded with α – particles of energy 5 MeV, which emitted a highly penetrating radiation.
- The equation for above process can be written as
- The radiations are not effected by electric and magnetic fields.
- In 1932, James Chadwick, had subjected nitrogen and argon to the beryllium radiation. He interpreted the experimental results by assuming that the radiation is of a new kind of particles which has no charge and its mass is equal to proton. These neutral particles were named as ‘neutrons’. Thus the neutron was discovered.
- The experimental results can be represented by the following equation.
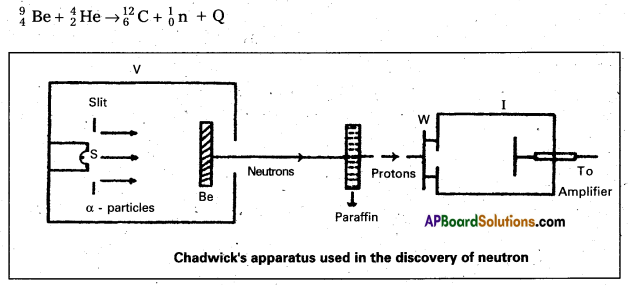
Question 3.
What are the properties of a neutron ?
Answer:
- Neutron is an uncharged particle and hence it is not deflected by the electric and magnetic fields.
- It has very high penetrating power and has very low ionization power.
- Inside the nucleus neutrons appear to be stable. The average life of an isolated neutron is about 1000 seconds. A free neutron is unstable and spontaneously decays into a proton, electron and an antineutrino \((\bar{v})\).
- If fast neutrons pass through substances like heavy water, paraffin wax, graphite etc., they are slowed down.
- Neutrons are diffracted by crystals.
![]()
Question 4.
What are nuclear forces ? Write their properties.
Answer:
The forces which hold the nucleons together in nucleus are called nuclear forces. Properties of Nuclear forces :
- Nuclear forces are attractive forces between proton and proton (P – P), proton and neutron (P – N) and neutron and neutron (N – N).
- Nuclear forces are independent of charge. It was found that force between proton and proton is same as force between neutron and neutron.
- These forces are short range forces i.e., these forces will act upto a small distance only. Generally the range of nuclear forces is upto few Fermi (10-15 m).
- These forces are non central forces, i.e., they do not act along the line joining the two nucleons.
- These forces are exchange forces. The force between two nucleons is due to exchange of π-mesons.
- These forces are spin dependent. These forces are strong when the spin of two nucleons are in same direction and they are weak when they are in opposite direction.
- Nuclear forces are saturated forces i.e., the force between nucleons will extend upto the immediate neighbouring nucleons only.
- These are the strongest forces in nature. They are nearly 1038 times stronger than gravitational forces and nearly 100 times stronger than Coulombic forces.
Question 5.
For greater stability a nucleus should have greater value of binding energy per nucleon. Why?
Answer:
- Uranium has a relatively low binding energy per nucleon as 7.6 MeV Hence to attain greater stability Uranium breaks up into intermediate mass nuclei resulting in a phenomenon called nuclear fission.
- Lighter nuclei such as hydrogen combine to form heavy nucleus to form helium for greater stability, resulting in a phenomenon called nuclear fusion.
- Iron whose binding energy per nucleon stands maximum at 8.7 MeV is the most stable and will undergo neither fission nor fusion.
Question 6.
Explain α – decay ?
Answer:
- It is the phenomenon of emission of an a particle from a radioactive nucleus. When a nucleus emits an alpha particle, its mass number decreases by 4 and charge number decreases by 2.
- In general, alpha decay is represented as
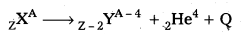
Where Q is the energy released in the decay. - Thus the total mass energy of the decay products is less than the mass energy of the original nuclide.
- The difference between the initial mass energy and the total mass energy of decay products is called disintegration energy (Q) of the process.
- This can be calculated using Einstein’s mass energy equivalence relation, E = (Δm). c2
i-e., Q = (mx – my – mHe) c2
The energy released (Q) is shared by daughter nucleus y and alpha particle.
Question 7.
Explain β – decay ?
Answer:
- It is the phenomenon of emission of an electron from a radioactive nucleus.
- When a parent nucleus emits a β-particle (i.e., an electron), mass number remains same because mass of electron is negligibly low. However, the loss of unit negative charge is equivalent to a gain of unit positive charge. Therefore, atomic number is increased by one.
- In general, we can write
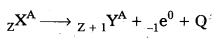
where Q is the energy released in β-decay. - The basic nuclear process underlying p-decay is the conversion of neutron to proton.
n → P + \(\overline{\mathrm{e}}\) + \(\overline{\mathrm{v}}\)
While for β+ decay, it is the conversion of proton ino neutron.
P → n + e+ + v - The emission of electron in β-decay is accompained by the emission of an anti neutrino \((\bar{v})\) In β, decay instead, a neutrino (v) is generated. Neutrons are neutral particles with very small mass compared to electrons. They have only weak interactions with other particles.
![]()
Question 8.
Explain γ – decay ?
Answer:
- It is the phenomenon of emission of gamma ray photon from a radioactive nucleus.
- Like an atom, a nucleus has discrete energy levels in the ground state and excited states.
- When a nucleus in an excited state spontaneously decays to its ground state (or to a lower energy state), a photon is emitted with energy equal to the difference in the two energy levels of the nucleus. This is the so called gamma-decay.
- The energy (MeV) corresponds to radiation of extremely short wave length, shorter than the hard X-ray region.
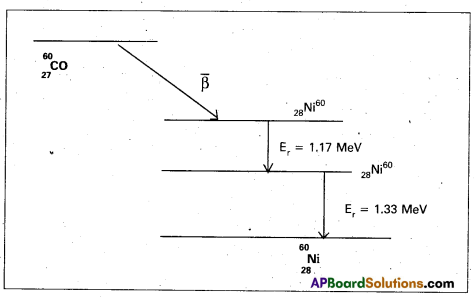
- A Gamma ray is emitted when a or p decay results in a daughter nucleus in an excited
state. - The \(\bar{\beta}\) -decay of 27CO60 transforms it into an excited 28Ni60 nucleus. This reaches the ground state by emission of γ-rays of energy 1.17 MeV and 1.33 MeV. This is shown in figure.
Question 9.
Define half life period and decay constant for a radioactive substance. Deduce the relation between them.
Answer:
Half life period (T) : Time taken for the number of radio active nuclei to disintegrate to half of its original number of nuclei is called Half life period.
Decay constant (λ) : The ratio of the rate of radioactive decay to the number of nuclei present at that instant.
It is a proportional constant and is denoted by ‘λ’.
λ = \(\frac{-\left(\frac{\mathrm{dN}}{\mathrm{dt}}\right)}{\mathrm{N}}\)
Relation between half the period and decay constant:
- The radioactive decay law N = N0 e-λt states that the number of radioactive-nuclei in a radioactive sample decreases exponentially with time. Here λ is called decay constant.
- If N0 is the number of nuclei at t = 0 and N is the radioactive nuclei at any instant of time’t’.
- Substituting N = \(\frac{\mathrm{N}_0}{2}\) at t = T in N = N0e-λt.
Where T is half life of the radioactive substance. - \(\frac{\mathrm{N}_0}{2}\) = N0 e-λT
eλT = 2
λT = ln2
T = \(\frac{\ln 2}{\lambda}\) = \(\frac{2.303 \log _{10}^2}{\lambda}\)
∴ T = \(\frac{0.693}{\lambda}\)
Question 10.
Define average life of a radioactive substance. Obtain the relation between decay constant and average life.
Answer:
Average life \((\tau)\) : It is equal to the total life time of all the N0 nuclei divided by the total number of original nuclei N0. It is denoted by \((\tau)\).
Relation between decay constant and average life :
- Let N0 be the radioactive nuclei that are present at t = 0 in the radioactive sample; The no’ of nuclei which decay between t and t + dt is dN.
- The total life time of these dN nuclei is t dN. The total life time of all the nuclei present initially in the sample = \(\int_0 \mathrm{t} \mathrm{dN}\)
- Average life time \((\tau)\) is equal to the total life time of all the N0 nuclei divided by the total number of original nuclei N0.
- Average \((\tau)\) = \(\frac{\int \mathrm{tdN}}{\mathrm{N}_0}\)
But \(\frac{\mathrm{dN}}{\mathrm{dt}}\) = -λN
dN = -λNdt = N0e-λtdt [∵ N = N0e-λt] 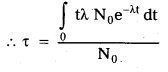
On integrating, we get \(\tau\) = \(\frac{1}{\lambda}\)
\(\tau\) = \(\frac{T}{0.693}\) [∵ λ = \(\frac{0.693}{\mathrm{~T}}\)]- From the above equation ‘the reciprocal of the decay constant gives us the average life of a radioactive sample.
Question 11.
Deduce the relation between half life and average life of a radioactive substance.
Answer:
Relation between half life (T) and average life (\(\tau\)) :
- We know, the radioactive decay law, N = N0 e-λt —– (1)
- Consider, ‘N0‘ is the number of nuclei present at t = 0 and after time T, only \(\frac{\mathrm{N}_0}{2}\) are left and after a time ‘2T’, only \(\frac{\mathrm{N}_0}{4}\) remain and soon.
- Substituting N = \(\frac{\mathrm{N}_0}{2}\) at t = T in eqn. (1) then
\(\frac{\mathrm{N}_0}{2}\) = N0 e-λT ⇒ \(\frac{1}{2}\) = \(\frac{1}{\mathrm{e}^{\lambda \mathrm{T}}}\) ⇒ eλT = 2
Taking loge on both sides, we get
λT = \(\log _{\mathrm{e}}^2\) = 2.303 \(\log _{\mathrm{e}}^2\) = 0.693
∴ T = \(\frac{0.693}{\lambda}\) —— (2) - Average life \(\tau\) = \(\frac{\int \mathrm{tdN}}{\mathrm{No}}\)
- But –\(\frac{\mathrm{dN}}{\mathrm{dt}}\) = λN dN = -λ.N0 e-λt dt [∵ from eqn. (1)]
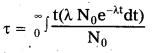
on integrating, we get \(\tau\) = \(\frac{1}{\lambda}\) —– (3)- From equs (2) and (3) we get \(\tau\) = \(\frac{\mathrm{T}}{0.693}\)
This is the relation between average life and half life of radioactive substance.
Question 12.
What is nuclear fission ? Give an example to illustrate it.
Answer:
Nuclear fission : The process of dividing a heavy nucleus into two or more smaller and stable nuclei due to nuclear reaction is called nuclear fission.
Ex : The fission reaction is
![]()
Where Q is the energy released.
Q = (Total mass of reactants – Total mass of product) C2
= [(Mass of \({ }_{92}^{235} \mathrm{U}\) + Mass of \({ }_0^1 n\)) – (Mass of \({ }_{56}^{141} \mathrm{Ba}\) + Mass of \({ }_{36}^{92} \mathrm{Kr}\) + Mass of three neutrons)]C2
= (235.043933 – 140.9177 – 91.895400 – 2 × 1.008665) amu × C2.
= 0.2135 × 931.5 MeV = 198.9 MeV = 200 MeV
![]()
Question 13.
What is nuclear fusion ? Write the conditions for nuclear fusion to occur.
Answer:
Nuclear fusion : The process of combining lighter nuclei to produce a larger nucleus is known as nuclear fusion.
E.g : Hydrogen nuclei (1H1) are fused together to form heavy Helium (2He4) along with 25.71 MeV energy released.
Conditions for nuclear fusion :
- Nuclear fusion occurs at very high temperatures such as 107 kelvin and very high pressures. These are obtained under the explosion of an atom bomb.
- Higher density is also desirable so that collisions between light nuclei occur quite frequently.
Question 14.
Distinguish between nuclear fission and nuclear fusion.
Answer:
Nuclear fission
- In this process heavy nucleus is divided into two fragments along with few neutrons.
- These reactions will takes place even at room temperature.
- To start fission atleast one thermal neutron from out side is compulsory.
- Energy released per unit mass of participants is less.
- In this process neutrons are liberated.
- This reaction can be controlled.
Ex: Nuclear reactor. - Atom bomb works on principle of fission reaction.
- The energy released in fission çan be used for peaceful purpose.
Ex : Nuclear reactor and Atomic power stations.
Nuclear fusion
- In this process lighter nuclei will join together to produce heavy nucleus.
- These reactions will takes place at very high temperature such as Kelwin.
- No necessary of external neutrons.
- Energy released per unit mass of participants is high. Nearly seven times more than fission reaction.
- In this process positrons are liberated.
- There is no control on fusion reaction.
- Hydrogen bomb works on the principle of fusion reaction.
- The energy released in fusion cannot be used for peaceful purpose.
Question 15.
Explain the terms tchain reaction’ and multiplication factor’. How is a chain reaction sustained?
Answer:
Chain reaction : In nuclear fission nearly three neutrons are produced when one uranium atom is destoryed. If they again participate in fission reaction nine neutrons are produced. In next generation the neutrons becomes 27. In this process the number of neutrons increases in geometric progression and the whole uranium is destroyed in few seconds. This type of self sustained fission reaction is called chain reaction.
Neutron multiplication factor (K) : Neutron multiplilcation factor is defined as the ratio of number of neutrons produced in one generation to the number of neutrons in previous generation.
![]()
Neutron multiplication factor is useful to understand the nature of nuclear reactions in a nuclear reactor.
To sustained chain reaction:
1. Neutron multiplication factor K ≥ 1.
Long Answer Questions
Question 1.
Define mass defect and binding energy. How does binding energy per nucleon vary with mass number ? What is its significance ?
Answer:
- Mass defect (ΔM) : The difference in mass of a nucleus and its constituents is called the mass defect. The nuclear mass M is always less than the total mass, Σm, of its constituents.
Mass defect, (ΔM) = [Zmp + (A – Z)mn – M] - Binding energy: The energy required to break the nucleus into its constituent nucleons is called the binding energy.
Binding Energy, (Eb) = ΔMC2 = [Zmp + (A – Z)mn – M] 931.5 MeV
Nuclear binding energy is an indication of the stability of the nucleus.
Nuclear binding energy per nucleon Ebn = \(\frac{\mathrm{E}_{\mathrm{b}}}{\mathrm{A}}\). - The following graph represents how the binding energy per nucleon varies with the mass number A.
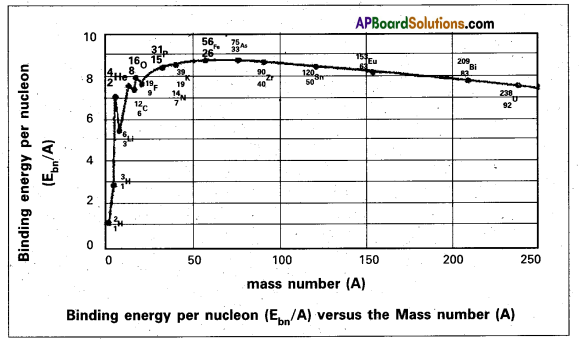
- From the graph that the binding energy is highest in the range 28 < A < 138. The binding energy of these nuclei is very close to 8.7 MeV.
- With the increase in the mass number the binding energy per nucleon decreases and consequently for the heavy nuclei like Uranium it is 7.6 MeV
- In the region of smaller mass numbers, the binding energy per nucleon curve shows the characteristic minima and maxima.
- Minima are associated with nuclei containing an odd number of protons and neutrons such as \({ }_3^6 \mathrm{Li}\), \({ }_5^{10} \mathrm{~B}\), \({ }_7^{14} \mathrm{~N}\) and the maxima are associated with nuclei having an even number of protons and neutrons such as \({ }_2^4 \mathrm{He}\), \({ }_6^{12} \mathrm{C}\), \({ }_8^{16} \mathrm{O}\).
Significance : - The curve explains the relationship between binding energy per nucleon and stability of the nuclei.
- Uranium has a relatively low binding energy per nucleon as 7.6 MeV. Hence to attain greater stability Uranium breaks up into intermediate mass nuclei resulting in a phenomenon called fission.
- On the other hand light nuclei such as hydrogen combine to form heavy nucleus to form helium for greater stability, resulting in a phenomenon called fusion.
- Iron is the most stable having binding energy per nucleon 8.7 MeV and it neither undergoes fission per fusion.
![]()
Question 2.
What is radioactivity ? State the law of radioactive decay. Show that radioactive decay is exponential in nature.
Answer:
- Radioactivity : .The nuclei of certain elements disintegrate spontaneously by emitting alpha (α), beta (β) and gamma (γ) rays. This phenomenon is called Radioactivity or Natural radioactivity.
- Law of radioactivity decay: The rate of radioactive decay \(\left(\frac{\mathrm{dN}}{\mathrm{dt}}\right)\) (or) the number of nuclei decaying per unit time at any instant, is directly proportional to the number of nuclei (N) present at that instant is called law of radioactivity decay’.
- Radioactive decay is exponential in nature : Consider a radioactive substance. Let the number of nuclei present in the sample at t = 0, be N0 and let N be the radioactive nuclei remain at an instant t.
\(\frac{\mathrm{dN}}{\mathrm{dt}}\) ∝ N ⇒ \(\frac{\mathrm{dN}}{\mathrm{dt}}\) = -λN
dN = -λNdt ——— (1)
The proportionality constant λ is called decay constant or disintegration constant. The negative sign indicates the decrease in the number of nuclei. - From eq.(1) \(\frac{\mathrm{dN}}{\mathrm{N}}\) = -λ dt ——- (2)
- Integrating on both sides
\(\int \frac{\mathrm{dN}}{\mathrm{N}}\) = \(-\lambda \int \mathrm{dt}\)
In N = -λt + C ——- (3)
Where C = Integration constant. - At t = O; N = N0. Substituting in eq. (3), we get in ln N0 = C
∴ ln N – ln N0 = – λt
ln \(\left(\frac{\mathrm{N}}{\mathrm{N}_0}\right)\) = – λt
∴ N = 0e-λt
The above equation represents radioactive decay law. - It states that the number of radioactive nuclei in a radioactive sample decreases exponentially with time.
Question 3.
Explain the principle and working of a nuclear reactor with the help of a labelled diagram. (A.P.Mar.’19,’16, ’15 & T.S. Mar. ‘15) (Mar. ’14)
Answer:
Principle : A nuclear reactor works on the principle of achieving controlled chain reaction in natural Uranium 238U enriched with 235U, consequently generating large amounts of heat.
A nucleàr reactor consists of
(1) Fuel
(2) Moderator
(3) Control rods
(4) Radiation shielding
(5) Coolant.
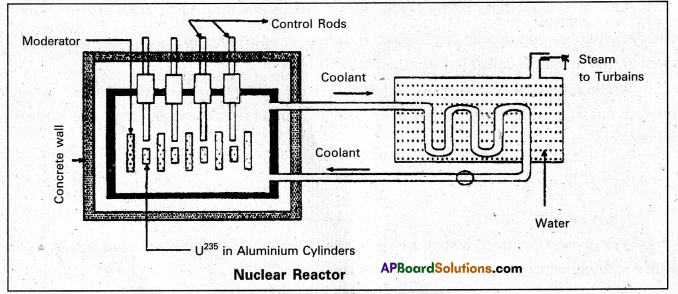
1. Fuel and clad : In reactor the nuclear fuel is fabricated in the form of thin and long cylindrical rods. These group of rods treated as a fuel assembly. These rods are surrounded by coolant, which is used to transfer of heat produced in them. A part of the nuclear reactor which use to store the nuclear fuel is called the core of the reactor. Natural uranium, enriched uranium, plutonium and uranium – 233 are used as nuclear fuels.
2. Moderator : The average energy of neutrons released in fission process is 2 MeV They are used to slow down the velocity of neutrons. Heavy water or graphite are used as moderating materials in reactor.
3. Control Rods : These are used to control the fission rate in reactor by absorbing the neutrons. Cadmium and boron are used as controlling the neutrons, in the form of rods.
4. Shielding : During fission reaction beta and gamma rays are emitted in addition to neutrons. Suitable shielding such as steel, lead, concrete etc are provided around the reactor to absorb and reduce the intensity of radiations to such low levels that do not harm the operating personnel.
5. Coolant: The heat generated in fuel elements is removed by using a suitable coolant to flow around them. The coolants used are water at high pressures, molten sodium etc.
Working: Uranium fuel rods are placed in the aluminium cylinders. The graphite moderator is placed in between the fuel cylinders. To control the number of neutrons, a number of control rods of cadmium or beryllium or boron are placed in the holes of graphite block: When a few 235U nuclei undergo fission fast neutrons are liberated. These neutrons pass through the surrounding graphite moderator and loose their energy to become thermal neutrons.
These thermal neutrons are captured by 235U. The heat generated here is used for heating suitable coolants which in turn heat water and produce steam. This steam is made to rotate steam turbine and there by drive a generator of production for electric power.
![]()
Question 4.
Explain the source of stellar energy. Explain the carbon – nitrogen cycle, proton – proton cycle occurring in stars.
Answer:
Scientists proposed two types of cyclic processes for the sources of energy in the sun and stars. The first is known as carbon-nitrogen cycle and the second is proton-proton cycle.
1. Carbon-Nitrogen Cycle: According to Bethe carbon – nitrogen cycle is mainly responsible for the production of solar energy. This cycle consists of a chain of nuclear reactions in which hydrogen is converted into Helium, with the help of Carbon and Nitrogen as catalysts. The nuclear reactions are as given below.
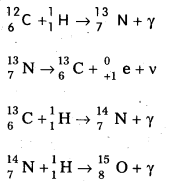

2. Proton – Proton Cycle: A star is formed by the condensation of a large amount of matter at a point in space. Its temperature rises to 2,00,000°C as the matter contracts under the influence of gravitational attraction. At this temperature the thermal energy of the protons is sufficient to form a deuteron and a positron. The deuteron then combines with another proton to form lighter nuclei of helium \({ }_2^3 \mathrm{He}\). Two such helium nuclei combine to form a helium nucleus \({ }_2^4 \mathrm{He}\) and two protons releasing a total amount of energy 25.71 MeV The nuclear fusion reactions are given below.
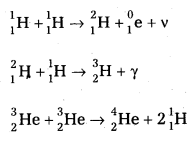
The net result is
![]()
Problems
Question 1.
Show that the density of a nucleus does not depend upon its mass number (density is independent of mass)
Solution:
Density of nucleus matter =
![]()
No. of nucleons (A) × mass of nucleons (m)
Volume of nucleus V = \(\frac{4}{3} \pi R^3\)
But R = R0A1/3
∴ V = \(\frac{4}{3} \pi \mathrm{R}_0^3 \mathrm{~A}\)
∴ Density of nucleus matter = \(\frac{\mathrm{Am}}{\frac{4}{3} \pi \mathrm{R}_0^3 \mathrm{~A}}\) = \(\frac{3 \mathrm{~m}}{4 \pi \mathrm{R}_0^3}\)
∴ Density of nucleus is independent of mass.
Question 2.
Compare the radii of the nuclei of mass numbers 27 and 64.
Solution:
A1 = 27; A2 = 64
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}\) = \(\left[\frac{\mathrm{A}_1}{\mathrm{~A}_2}\right]^{1 / 3}\) [∵ R = R0A1/3]
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}\) = \(\left[\frac{27}{64}\right]^{\frac{1}{3}}\) = \(\frac{3}{4}\)
∴ R1 : R2 = 3 : 4
Question 3.
The radius of the oxygen nucleus \({ }_8^{16} \mathrm{O}\) is 2.8 × 10-15m. Find the radius of lead nucleus \({ }_{82}^{205} \mathrm{~Pb}\).
Solution:
R0 = 2.8 × 10-15 m; A0 = 16
APb = 205; RPb = ?
\(\frac{R_{P b}}{R_0}\) = \(\left[\frac{A_{P b}}{A_0}\right]^{1 / 3}\) = \(\left[\frac{205}{16}\right]^{1 / 3}\)
[∵ R = R0A1/3]
\(\frac{R_{P b}}{2.8 \times 10^{-15}}\) = (12.82)1/3 = 2.34
RPb = (2.34) × (2.8 × 10-15)
= 6.55 × 10-15m
![]()
Question 4.
Find the binding energy of \({ }_{26}^{56} \mathrm{Fe}\). Atomic mass of Fe is 55.9349u and that of Hydrogen is 1.00783u and mass of neutron is 1.00876u.
Solution:
Mass of hydrogen atom
mp = 1.00876u; mn = 1.00867u
Z = 26; A = 56
Mass of Iron atom M = 55.9349u
i) Mass defect Δm
= [Zmp + (A – Z) mn – M]
= [26 × 1.00876 + (56 – 26) (1.00867) – 55.9349] u
∴ Δm = 0.55296u
ii) BE of nucleus = ΔMC2
= ΔM × 931.5 MeV
= 0.55296 (931.5) MeV
= 515.08 MeV
Question 5.
How much energy is required to separate the typical middle mass nucleus \({ }_{50}^{120} \mathrm{Sn}\) into its constituent nucleons? (Mass of \({ }_{50}^{120} \mathrm{Sn}\) = 119.902199u, and mass of neutron = 1.008665u)
Solution:
mp = 1.007825u
mn = 1.008665u
For Sn, Z = 50;
A = 120; M = 119.902199u
i) Mass defect Δm
= [Zmp + (A – Z)mn – M]u
= 50 (1.007825) + (120 – 50) [(1.008665) – 119.902 199]
= [150 × 1.007825 + 70 × 1.008665 – 119.902199]u
= [50.39125 + 70.60655 – 119.902199]u
ΔM = [120.9978 – 119.902199]
= 1095601u
ii) Energy required to šeparate the nucleons = B.E of the nucleus
BE = ΔMc2 = ΔM × 931.5MeV
= 1.095601 × 931.5 MeV
= 1020.5 MeV
Question 6.
Calculate the binding energy of an α-particle. Given that mass of proton = 1.0073 u, mass of neutron = 1.0087u, and mass of α- particle = 4.0015u.
Solution:
For 2He4, A = 4, Z = 2, mp = 1.0073u
mn = 1.0087u, mn = 4.0015u
i) ΔM
= [Zmp + (A – Z)mn – M]
= [2(1.0073) + (4 – 2) (1.0087) – 4.00260]
= [2 × 1.0073 + 2 × 1.0087 – 4.00260]
= (2.0146 + 2.0174) – 4.0015
ΔM = [4.032 – 4.0015] = 0.0305 u
ii) BE = ΔM × c2 = ΔM × 931.5 MeV
= 0.0305 × 931.5
∴ BE = 28.41 MeV
![]()
Question 7.
Find the energy required to split \({ }_8^{16} \mathrm{O}\) nucleus into four α-particles. The mass of an α-particle is 4.002603u and that of oxygen is 15.994915u.
Solution:
The energy required to split O =
[Total mass of the products – Total mass of the reactants] c2
Mass of four \({ }_2^4 \mathrm{He}\) – Mass of \({ }_8^{16} \mathrm{O}\)] × c2
= [(4 × 4.002603) – 15.994915] u × c2
= [16.010412 – 15.994915] u × c2
= (0.015497) 931.5 MeV
= 14.43 MeV
Question 8.
Calculate the binding energy per nucleon of \({ }_{17}^{35} \mathrm{Cl}\) nucleus. Given that mass of \({ }_{17}^{35} \mathrm{Cl}\) nucleus = 34.98000 u, mass of proton = 1.007825u, mass of neutron = 1.008665u and 1 is equivalent to 931 MeV.
Solution:
For \({ }_{17}^{36} \mathrm{Cl}\), A = 35, Z = 17;
mp = 1.007825 u
mn = 1.008665 u,
M = 34.98u
(i) ΔM = [Zmp + (A – Z) mn – M]
= [17 × 1.007825 + (35 – 17)(1.008665) – 34.98]
= [17.13303 + 18.15597 – 34.98]
ΔM = [35.289 – 34.98]
= 0.3089 u
(ii) BE = ΔMc2
= 0.3089 × 931 MeV = 287.5859 MeV
∴ BE per nucleon
= \(\frac{B \cdot E}{A}\) = \(\frac{287.5859}{35}\) = 8.21 MeV
Question 9.
Calculate the binding energy per nucleon of \({ }_{20}^{40} \mathrm{Ca}\). Given that mass of \({ }_{20}^{40} \mathrm{Ca}\) nucleus = 39.962589u, mass of a proton = 1.007825 u,; mass of Neutron = 1.008665u and 1u is equivalent to 931 MeV.
Solution:
For \({ }_{20}^{40} \mathrm{C}\), A = 40, Z = 20; mp = 1.007825 u
mn = 1.008665 u; M = 39.962589 u
(i) ΔM = [Zmp + (A – Z) mn – M]
= [(20) (1.007825) + (40 – 20)(1 .008665) – 39.962589]
[(20 × 1.007825) + (20 × 1.008665) – 39.962589]
= [40.3298 – 39.962589] = 0.3672 u
(ii) BE = ΔMc2 = 0.3672 × 931 MeV
= 341.86 MeV
B.E ‘341.86
(iii) B.E per nucleon = \(\frac{B . E}{A}\) = \(\frac{341.86}{40}\)
= 8.547 MeV
Question 10.
Calculate
(i) mass defect,
(ii) binding energy and
(iii) the binding energy per nucleon of \({ }_6^{12} \mathrm{C}\) nucleus. Nuclear mass of \({ }_6^{12} \mathrm{C}\) = 12.000000 u; mass of proton = 1.007825 u and mass of neutron = 1.008665 u.
Solution:
For \({ }_6^{12} \mathrm{C}\), A = 12; Z = 6; mp = 1.007825u
mn = 1.008665u; M = 12.000000u
(i) ΔM = [Zmp + (A – Z) mn – M]
= [6(1.007825) + (12 – 6)(1.008665) – 12,00]
= [6 × 1.007825 + 6 × 1.008665 – 12]
= [6.04695 + 6.05199 – 12.00]
ΔM = [12.09894 – 12.00] = 0.098944
(ii) BE = ΔM × c2 = 0.09894 × 931.5 MeV
= 92.16 MeV
(iii) BE per nucleon
= \(\frac{B . E}{A}\) = \(\frac{92.16}{12}\) = 7.68 MeV
![]()
Question 11.
The binding energies per nucleon for deuterium and helium are 1.1 MeV and 7.0 MeV respectively. What energy in joules will be liberated when 106 deuterons take part in-the reaction.
Solution:
\(\left[\frac{B \cdot E}{A}\right]_D\) = 1.1 MeV; \(\left[\frac{B . E}{A}\right]_{H e}\) = 7.0 MeV
For deuterium \(\left({ }_1^2 \mathrm{H}\right)\),
A = 2
For He \(\left({ }_2^4 \mathrm{He}\right)\), A = 4
\(\left[\frac{B \cdot E}{2}\right]_D\) = 1.1 MeV ⇒ [B.E.]D
= 2 × 1.1 MeV = 2.2 MeV
\(\left[\frac{B . E}{4}\right]_{\mathrm{He}}\) = 70 MeV ⇒ [B.E.]He
= 4 × 7.0 MeV = 28 MeV
We know 1H2 + 1H2 → 2He4
Energy released = B.E of 106 deuterons – B.E of \(\frac{1}{2}\) × 106 Helium atoms
B.E = 2.2 × 106 × \(\frac{1}{2}\) × 106 × 28
= 106(2.2 – 14)
= -11.8 × 106 MeV
= -11.8 × 106 × 1.6 × 10-13J
= -18.88 × 10-7 J
(- ve sign indicates that energy is released)
∴ Energy released = 18.88 × 10-7 J
Question 12.
Bombardment of lithium with protons gives rise to the following reaction :
\({ }_3^7 \mathrm{Li}\) + \({ }_1^1 \mathrm{H}\) → 2 \(\left[{ }_2^4 \mathrm{He}\right]\) + Q. Find the Q-value of the reaction. The atomic masses of lithium, proton and helium are 7.016u, 1.0084 and 4.004u respectively.
Solution:
Mass of Lithium = 7.0 16 u
mp = 1.008 u
Mass of Helium = 4004 u;
u = 931.5 MeV
Q = [Total mass of the reactants – Total mass of the products] c2
= [Mass of Lithium + mp – (2 × mass of Helium)] × 931.5 MeV
= [7.016+ 1.008 – 2(4.004)] × 931.5MeV
= [18.024 – 8.008] × 931.5 MeV
∴ Energy Q = 0.016 × 931.5
= 14.904 MeV
Question 13.
The half life radium is 1600 years. How much time does lg of radium take to reduce to 0.125 g. (T.S. Mar. ’16)
Solution:
Half life of radium = 1600 years
Initial mass = 1g
Final mass 0.125 g = \(\frac{1}{8}\) g
The quantity remaining after ‘n’ half lifes is \(\frac{1}{2^{\mathrm{n}}}\) of the initial quantity.
In this problem,
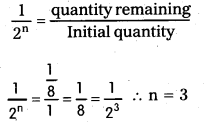
∴ Time taken = ’n’ half-lifes = 3 × 1600
= 4,800 years
Question 14.
Plutonium decays with a half – life of 24,000 years. If plutonium is stored for 72,000 years, what fraction of it remains ?
Solution:
Half-life of plutonium = 24,000 years
The duration of the time = 72,000 years
Initial mass = Mg
Final mass = mg
Number of half lifes (n)
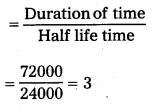
Fraction of plutonium that remains
![]()
![]()
Question 15.
A certain substance decays to 1/232 of its initial activity in 25 days. Calculate its half-life.
Solution:
Fraction of substance decays
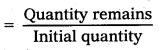
= \(\frac{1}{2^n}\) = \(\frac{1}{32}\) = \(\frac{1}{2^5}\)
∴ n = 5
Duration of time = 25 days
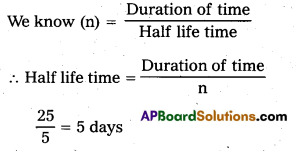
Question 16.
The half-life period of a radioactive substance is 20 days. What is the time taken for 7/8th of its original mass to disintegrate?
Solution:
Half life period = 20 days
In this problem,
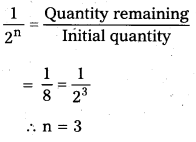
∴ Time taken to disintegrate
= n × Half life time
= 3 × 20 = 60 days
Question 17.
How many disintegrations per second will Occur in one gram of \({ }_{92}^{238} \mathrm{U}\), if its half-life against α-decay is 1.42 × 10-17s?
Solution:
T = 1.42 × 1017 sec
Decay constant (λ) = \(\frac{0.693}{\mathrm{~T}}\) = \(\frac{0.693}{1.42 \times 10^7}\)
No. of disintegration (n) in 1 gm
= \(\frac{1}{238}\) × 6.023 × 1023
∴ Activity A = λN
= \(\frac{0.693}{1.42 \times 10^{17}}\) × \(\frac{1}{238}\) × 6.023 × 1023
= 1.235 × 104 disintegrations / sec
Question 18.
The half-life of a radioactive substance is 100 years. Calculate in how many years the activity will decay to 1/10th of its initial value.
Solution:
T = 100 years
λ = \(\frac{0.693}{\mathrm{~T}}\) = \(\frac{0.693}{\mathrm{~T}}\) = 0.693 × 10-2 years
N = N0e-λt ⇒ e-λt = \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = \(\frac{1}{10}\)
eλt = 10 ⇒ λt = \(\log _e^{10}\) = 2.303 × \(\log _{10}^{10}\)
t = \(\frac{2.303 \times 1}{0.693 \times 10^{-2}}\) = 3.323 × 102
= 332.3years
Question 19.
One gram of radium is reduced by 2 milligram in 5 years by a-decay. Calculate the half-life of radium.
Solution:
Initial (original) mass (N0) = 1 gram
Reduced mass = 2 mg = 0.002 grams
Final mass (N) = 1 – 0.002 = 0.998 grams
t = 5 years
e-λt = \(\frac{\mathrm{N}}{\mathrm{N}_0}\) ⇒ eλt = \(\frac{\mathrm{N}_0}{\mathrm{~N}}\) ⇒ λt = \(\log _{\mathrm{e}}\left[\frac{\mathrm{N}_0}{\mathrm{~N}}\right]\)
λt = 2.303 log\(\left[\frac{\mathrm{N}_0}{\mathrm{~N}}\right]\)
λt = 2.303 log \(\left[\frac{1}{0.998}\right]\)
= 2.303 × 0.000868
= 0.001999
λ = \(\frac{0.001999}{5}\) = 0.0003998
T = \(\frac{0.693}{\lambda}\) = \(\frac{0.693}{0.0003998}\) = 1733.3 years
![]()
Question 20.
The half-life of a radioactive substance is 5000 years. In how many years, its activity will decay to 0.2 times a its initial value ? Given log105 = 0.6990.
Solution:
T = 5000 years; t = ?
Activity, A = Nλ = 0.2 times initial value
Initial activity A0 = N0λ
In radioactivity,
N = N0e-λt ⇒ \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = e-λt = 0.2
Put 0.2 = \(\frac{1}{5}\) ; \(\frac{1}{5}\) = e-λt (or) -λt = \(-\log _e^5\)
(or) t = \(\log _{\mathrm{e}}^5 \frac{5}{\lambda}\)
Radioactive decay constant A = \(\frac{\log _{\mathrm{e}} 2}{\mathrm{~T}}\)
= \(\frac{2.303 \log _{10}^2}{5000}\) = \(\frac{0.693}{5000}\)
Time taken to decay
t = \(\frac{\log _{\mathrm{e}}^5}{\lambda}\) × 5000
∴ t = \(\frac{2.303 \times 0.6990 \times 5000}{0.693}\) = \(\frac{8049}{0.693}\)
= 1.161 × 104 years
Question 21.
An explosion of atomic bomb releases an energy of 7.6 × 1013J. If 200 MeV energy is released of fission of one 235U atom calculate
(i) the number of uranium atoms undergoing fission,
(ii) the mass of uranium used in the bomb.
Solution:
Energy released (E) = 7.6 × 1013 J
Energy released on fissions (E) = 200 MeV
= 200 × 106 × 1.6 × 10-19 J
i) No. of fissions (n) = \(\frac{\mathrm{E}^{\prime}}{\mathrm{E}}\)
= \(\frac{7.6 \times 10^{13}}{200 \times 10^6 \times 1.6 \times 10^{-19}}\)
∴ n = 2.375 × 1024 atoms
But Avogadro number N = 6.023 × 1023 atoms
Mass of uranium (m) = \(\frac{\mathrm{n} \times 235}{\mathrm{~N}}\)
= \(\frac{2.375 \times 10^{24}}{6.023 \times 10^{23}}\)
= 926.66 g
Question 22.
If one microgram of \({ }_{92}^{235} \mathrm{U}\) is completely destroyed in an atom bomb, how much energy will be released ? (T.S. Mar. ’19)
Solution:
m = 1μg = 1 × 10-6 g = 1 × 10-6 × 10-3 kg
= 10-9 kg
c = 3 × 108 m/s
E = mc2 = 1 × 10-9 × 9 × 106 = 9 × 107 J
Question 23.
Calculate the energy released by fission from 2g of \({ }_{92}^{235} \mathrm{U}\) in kWh. Given that the energy released per fission is 200 MeV.
Solution:
Mass of uranium = 2g
Energy per fission = 200 MeV
No. of atoms in 2g, n = \(\frac{2 \times 6.023 \times 10^{23}}{235}\)
Total energy released (E’) = nE
= \(\frac{2 \times 6.023 \times 10^{23}}{235}\) × 200 × 106 × 1.6 × 10-19J
= \(\frac{2 \times 602.3}{235}\) × 32 × 109
= \(\frac{1640.3 \times 10^8}{36 \times 10^5}\)
∴ E’ = 45.56 × 103 kWh
= 4.556 × 104 kWh
![]()
Question 24.
200 MeV energy is released when one nucleus of 235U undergoes fission. Find the number of fissions per second required for producing a power of 1 megawatt.
Solution:
E = 200 MeV
P = 1 × 106W
P = \(\frac{\mathrm{nE}}{\mathrm{t}}\) ⇒ \(\frac{\mathrm{n}}{\mathrm{t}}\) = \(\frac{\mathrm{P}}{\mathrm{E}}\) = \(\frac{10^6}{200 \times 10^6 \times 1.6 \times 10^{-19}}\)
= \(\frac{1}{32}\) × 1018
= 3.125 × 106
Question 25.
How much 235U is consumed in a day in an atomic power house operating at 400 MW, provided the whole of mass 235U is converted into energy ?
Solution:
P = 400 MW = 400 × 106 W, c = 3 × 108 m/s
t = 24 hours = 24 × 60 × 60 sec
E = mc2
\(\frac{\mathrm{Pt}}{\mathrm{c}^2}\) = m [∵ P = \(\frac{E}{t}\)]
m = \(\frac{400 \times 10^{-6} \times 24 \times 60 \times 60}{9 \times 10^6}\)
= 384 × 10-6 kg
∴ Mass required = 384 × 10-6 × 103 g = 0.384 g
Textual Exercises
Question 1.
a) Two stable isotopes of lithium \({ }_3^6 \mathrm{Li}\) and \({ }_3^7 \mathrm{Li}\) have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
b) Boron has two stable isotopes, \({ }_5^{10} \mathrm{~B}\) and \({ }_5^{11} \mathrm{~B}\). Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811u. Find the abundances of \({ }_5^{10} B\) and \({ }_5^{11} \mathrm{~B}\).
Solution:
a) Atomic weight
= Weighted average of the isotopes.
= \(\frac{6.01512 \times 7.5+7.01600 \times 92.5}{(7.5+92.5)}\)
= \(\frac{45.1134+648.98}{100}\)
= 6.9414
b) Let relative abundance of 5B10 be x%
∴ Relative abundance 5B11 = (100 – x) %
Proceeding as above
10.811 = \(\frac{10.01294 x+i 1.00931 \times(100-x)}{100}\)
x = 19.9% and (100 – x) = 30.1%
Question 2.
The three stable isotopes of neon : \({ }_{10}^{20} \mathrm{Ne}\), \({ }_{10}^{21} \mathrm{Ne}\) and \({ }_{10}^{22} \mathrm{Ne}\) have respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99u, 20.99 u and 21.99u, respectively. Obtain the average atomic mass of Neon.
Solution:
The masses of three isotopes are 19.99u, 20.99 u, 21.99u
Their relative abundances are 90.51%, 10.27% and 9.22%
∴ Average atomic mass of Neon is
m = \(\frac{90.51 \times 19.99+0.27 \times 20.99+9.22 \times 21.99}{(90.51+0.27+9.22)}\)
= \(\frac{1809.29+5.67+202.75}{100}\) = \(\frac{2017.7}{100}\) = 20.17u
Question 3.
Obtain the binding energy (in MeV. of a nitrogen nucleus \(\left({ }_7^{14} \mathrm{~N}\right)\), given m \(\left({ }_7^{14} \mathrm{~N}\right)\) = 14.00307 u.
Solution:
7N14 Nucleius contains 7 protons and 7 neutrons
Mass defect (ΔM) = 7mH + 7mn – mN
= 7 × 1.00783 + 7 × 1.00867 – 14.00307
= 7.05481 + 7.06069 – 14.00307
= 0.11243μ
Binding energy = 0.11243 × 931 MeV
= 104.67 MeV
![]()
Question 4.
Obtain the binding energy of the nuclei \({ }_{26}^{56} \mathrm{~F}\) and \({ }_{83}^{209} \mathrm{Bi}\) in units of MeV from the following data : m\(\left({ }_{26}^{56} \mathrm{Fe}\right)\) = 55.934939 u, m\(\left({ }_{83}^{209} \mathrm{Bi}\right)\) = 208.980388 u
Solution:
(i) 26F56 nucleus contains 26 protons and (56 – 26) = 30 neutrons
Mass of 26 protons = 26 × 1.007825
= 26.26345 a.m.u
Mass of 30 neutrons = 30 × 1.008665
= 30.25995 amu
Total mass of 56 nucleons
= 56.46340 a.m.u
Mass of 26Fe56 Nucleus
= 55.934939 a.m.u
Mass defect Δm = 56.46340 – 55.934939
= 0.528461 a.m.u
Total binding energy = 0.524861 × 931.5 MeV
= 492.26 MeV
Average B.E per nucleon = \(\frac{492.26}{56}\)
= 8.790 MeV
(ii) 83Bi209 nucleus contains 83 protons and (209 – 83) = 126 neutrons
Mass of 83 protons = 83 × 1.007825
= 83.649475 a.m.u
Mass of 126 Neutrons = 126 × 1.008665
= 127.09170 a.m.u
Total mass of nucleons = 210.741260 a.m.u
Mass of 83Bi209 nucleus = 208.986388 a.m.u
Mass defect Δm = 210.741260 – 208.980388
= 1.760872
Total B.E = 1.760872 × 931.5 MeV
= 1640.26 MeV
Average B.E. per nucleon = \(\frac{1640.26}{209}\)
= 7.848 MeV
Hence 26Fe56 has greater B.E per nucleon than 83Bi209
Question 5.
A given coin has a mass of 3.0gi Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of 29Cu atoms (of mass 62.92960 u.
Solution:
Number of atoms in 3g coin =
\(\frac{6.023 \times 10^{23} \times 3}{63}\)
= 2.868 × 1022
Each atom of copper contains 29 protons and 34 neutrons. Therefore, mass defect of each atom= [29 × 1.00783 + 34 × 1.00867] – 62.92960 = 0.59225 u
Total mass defect for all the atoms
= 0.59225 × 2.868 × 1022 u
ΔM = 1.6985 × 1022u
As, 1u = 931 MeV
Nuclear energy required
= 1.6985 × 1022 × 931 MeV
= 1.58 × 1025 MeV
Question 6.
Write nuclear reaction equations for
i. α-decay of \({ }_{88}^{226} \mathrm{Ra}\)
ii. α-decay of \({ }_{94}^{242} \mathrm{Pu}\)
iii. β-decay of \({ }_{15}^{32} \mathrm{P}\)
iv. β-decay of \({ }_{83}^{210} \mathrm{Bi}\)
v. β+-decay of \({ }_6^{11} \mathrm{C}\)
vi. β+-decay of \({ }_{43}^{97} \mathrm{Tc}\)
Solution:
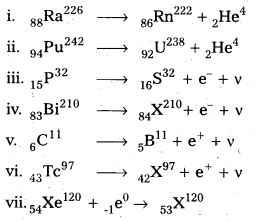
Question 7.
A radio active isotope has a half-life of T years. How long will it take the activity to reduce to
a) 3.125%,
b) 1% of its original value ?
Solution:
a) Here \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = \(\frac{3.125}{100}\) = \(\frac{1}{32}\)
From \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = \(\left(\frac{1}{2}\right)^{\mathrm{n}}\) = \(\frac{1}{32}\left(\frac{1}{2}\right)^5\) ∴ n = 5
From t = nT = 5T
b) Here \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = \(\frac{1}{100}\)
From \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = e-λt = \(\frac{1}{100}\)
-λt = log 1 – \(\log _{\mathrm{e}} 100\)
= 0 – 2.303 \(\log _{10} 100\) = -2.203 × 2
= -4.606
t = \(\frac{4.606}{\lambda}\) = \(\frac{4.606}{0.693 / \mathrm{T}}\) = 6.65 T
Question 8.
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive \({ }_6^{14} \mathrm{C}\) present with the stable carbon isotope \({ }_6^{12} \mathrm{C}\). When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity, ceases and its activity begins to drop. From the known half-life (5730 years. of \({ }_6^{14} \mathrm{C}\), and the measured activity, the age of the specimen can be approximately estimated. This is the principle of \({ }_6^{14} \mathrm{C}\) dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
Solution:
Here normal activity R0 = 15 decays/min
Present activity R = 9 decays / min
T = 5730 yrs
Age t = ?
As activity is proportional to the number of radio active atoms, therefore
\(\frac{\mathrm{N}}{\mathrm{N}_0}\) = \(\frac{\mathrm{R}}{\mathrm{R}_0}\) = \(\frac{9}{15}\)
But \(\frac{N}{N_0}\) = e-λt
e-λt = \(\frac{9}{15}\) = \(\frac{3}{5}\)
e+λt = \(\frac{5}{3}\)
λt \(\log _{\mathrm{e}} \mathrm{e}\) = \(\log _e \frac{5}{3}\) = 2.3023 log 1.6667
λt = 2.3026 × 0.2218 = 0.5109
t = \(\frac{0.5109}{\lambda}\)
λ = \(\frac{0.693}{T}\) = \(\frac{0.693}{5730}\)yt-1
∴ t = \(\frac{0.5109}{0.693 / 5730}\) = \(\frac{0.5109 \times 5730}{0.693}\)
t = 4224.3 years
![]()
Question 9.
Obtain the amount of \({ }_{27}^{60} \mathrm{Co}\) necessary to provide a radioactive source of 8.0 mCi strength. The half-life of \({ }_{27}^{60} \mathrm{Co}\) is 5.3 years.
Solution:
Here, mass of 27Co60 =?
Strength of source, \(\frac{\mathrm{dN}}{\mathrm{dt}}\) = 8.0 mci
= 8.0 × 3.7 × 107 disint/sec
Half life, T = 5.3 years
= 5.3 × 365 × 24 × 60 × 60 sec
= 1.67 × 108 sec
λ = \(\frac{0.693}{T}\) = \(\frac{0.693}{1.67 \times 10^8}\) = 4.14 × 10-9 s-1
As \(\frac{\mathrm{dN}}{\mathrm{dt}}\) = 2N
∴ N = \(\frac{\mathrm{dN} / \mathrm{dt}}{\lambda}\) = \(\frac{8 \times 3.7 \times 10^7}{4.14 \times 10^{-9}}\)
= 7.15 × 1016
By definition of Avogadros number, Mass of 6.023 × 1023 atoms of 27Co60 = 60 g
Mass of 7.15 × 1016 atoms of 27Co60
= \(\frac{60 \times 7.15 \times 10^{16}}{6.023 \times 10^{23}}\) = 7.12 × 10-6g
Question 10.
The half-life of \({ }_{38}^{90} \mathrm{~Sr}\) is 28 years. What is the disintegration rate of 15 mg of this isotope?
Solution:
Here T = 28 years = 28 × 3.154 × 107s
As number of atoms in 90 g of 38Sr90
= 6.023 × 1023
∴ Number of atoms in 15mg of 38Sr90
= \(\frac{6.023 \times 10^{23}}{90}\) × \(\frac{15}{1000}\)
i.e., N = 1.0038 × 1020
Rate of disintegration \(\frac{\mathrm{dN}}{\mathrm{dt}}\) = λN
= \(\frac{0.693}{\mathrm{~T}} \mathrm{~N}\)
= \(\frac{0.693 \times 1.0038 \times 10^{20}}{28 \times 3.154 \times 10^7}\)
= 7.877 × 1010 Bq
Question 11.
Obtain approximately the ratio of the nuclear radii of the gold isotope \({ }_{79}^{197} \mathrm{Au}\) and the silver isotope \({ }_{47}^{107} \mathrm{Ag}\).
Solution:
Here A1 = 197 and A2 = 107
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}\) = \(\left(\frac{\mathrm{A}_1}{\mathrm{~A}_2}\right)^{1 / 3}\) = \(\left(\frac{197}{107}\right)^{1 / 3}\) = 1.225
Question 12.
Find the Q-value and the kinetic energy of the emitted α-particle in the α-decay of (a) \({ }_{88}^{226} \mathrm{Ra}\) and (b) \({ }_{86}^{220} \mathrm{Rn}\).
Given m \(\left({ }_{88}^{226} \mathrm{Ra}\right)\) = 226.02540 u,
m \(\left({ }_{86}^{222} R n\right)\) = 222.01750 u,
m \(\left({ }_{86}^{222} \mathrm{Rn}\right)\) =220.01137 u, m \(\left({ }_{84}^{216} \mathrm{Po}\right)\) = 216.00189 u.
Solution:
a) 88Ra226 → 85Rn222 + 2He4 Q value
[m(88Ra226) – m(86Rn222) – mα] × 931.5 MeV
= [226.02540 – 222.0 1750 – 4.00260] × 931.5 MeV
Q = 0.0053 × 931.5 MeV = 4.94 MeV
K.E of a particle =
\(\frac{(A-4) Q}{A}\) = \(\frac{226-4}{226}\) × 4.94 = 4.85 MeV
b) Proceeding as above, in case of
Q = 6.41 MeV
K.E of a particle
= \(\frac{(\mathrm{A}-4) \mathrm{Q}}{\mathrm{A}}\) = \(\frac{(220-4)}{220}\) × 6.41 = 6.29 MeV
Question 13.
The radionuclide 11C decays according to ![]() The maximum energy of the emitted positron is 0.960 MeV. Given the mass values ; m\(\left({ }_6^{11} \mathrm{C}\right)\) = 11.011434u and \(\left({ }_6^{11} \mathrm{~B}\right)\) = 11.009305 u, calculate Q and compare it with the maximum energy of the positron emitted.
The maximum energy of the emitted positron is 0.960 MeV. Given the mass values ; m\(\left({ }_6^{11} \mathrm{C}\right)\) = 11.011434u and \(\left({ }_6^{11} \mathrm{~B}\right)\) = 11.009305 u, calculate Q and compare it with the maximum energy of the positron emitted.
Solution:
Mass defect in the given reaction is Δm = m(6C11)
= [m (5B11) + Me]
This is in terms of nuclear masses. If we express the Q value interms of atomic masses we have to subtract 6me from atomic mass of carbon and 5 me from that of boron to get the corresponding nuclear masses
Therefore, we have
Δm = [m(6C11) – 6 me – m(5B11) + 5me – me
= [m(6C11) – m(5B11) – 2 me]
= [11.011434 – 11.009305 – 2 × 0.000548] u
= 0.001033u
As, 1u = 931 MeV
Q = 0.001033 × 931 MeV = 0.961 MeV
Which is the maximum energy of emitted position.
Question 14.
The nucleus \({ }_{10}^{23} \mathrm{Ne}\) decays by β-emission. Write down the β – decay. Write down the β-decay equation and determine the maximum kinetic energy of the electrons emitted. Given that:
\(m\left({ }_{10}^{23} \mathrm{Ne}\right)\) = 22.994466 u
\(\mathrm{m}\left({ }_{11}^{23} \mathrm{Na}\right)\) = 22.089770 u.
Solution:
The β decay of 10Ne23 may be represented as
10Ne23 → 11Na23 – 1e0 + v + Q
Ignoring the rest mass of antineutrino and v electron
Mass defect, Δm = m(10Ne23) – m (11Na23)
= 22.994466 – 22.989770
= 0.004696 amu
Q = 0.004696 × 931 MeV
= 4.372 MeV
As 11Na23 is very massive, this energy of 4.3792 MeV is shared by e–v pair. The max K.E of e– = 4.372 MeV when energy carried by v is zero.
Question 15.
The Q value of a nuclear reaction A + b → C + d is defined by Q = [mA + mb – mc – md] c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
i) \(\mathrm{H}_{\mathrm{1}}^{\mathrm{1}}\) + \({ }_1^3 \mathrm{H}\) → \({ }_1^2 \mathrm{H}\) + \({ }_1^2 \mathrm{H}\)
ii) \({ }_6^{12} \mathrm{C}\) + \({ }_6^{12} \mathrm{C}\) → \({ }_{10}^{20} \mathrm{Ne}\) + \({ }_2^4 \mathrm{He}\)
Atomic masses are given to be
\(\mathrm{m}\left({ }_{\mathrm{1}}^2 \mathrm{H}\right)\) = 2.014102u
\(\mathrm{m}\left({ }_1^3 \mathrm{H}\right)\) = 3.016049 u
\(\mathrm{m}\left({ }_6^{12} \mathrm{C}\right)\) = 12.000000u
\(\mathrm{m}\left({ }_{10}^{20} \mathrm{Ne}\right)\) = 19.992439 u
Solution:
i) \(\mathrm{H}_{\mathrm{1}}^{\mathrm{1}}\) + \({ }_1^3 \mathrm{H}\) → \({ }_1^2 \mathrm{H}\) + \({ }_1^2 \mathrm{H}\)
Q = Δm × 931 MeV =
[m (1H1 + m(1H3) – 2m (1H2)] × 931 MeV
= [1.007825 + 3.01604 – 2 × 2.014102] × 931 MeV
= -4.03 MeV
∴ This reaction is endothermic,
ii) 6C12 + 6C12 → 10Ne20 + 2He4
Q = Δm × 931 MeV =
[2m(6C12) – m(10Ne20) – m(2He4)] × 931 MeV
= [24.000000 – 19.992439 – 4.002603] × 931 MeV
= ±4.61 MeV
∴ The reaction is exothermic.
Question 16.
Suppose we think of fission of a \({ }_{26}^{56} \mathrm{Fe}\) nucleus into two equal fragments, \({ }_{13}^{28} \mathrm{Al}\), Is the fission energetically possible ? Argue by working out Q of the process. Given \(\mathrm{m}\left({ }_{26}^{56} \mathrm{Fe}\right)\) = 55.93494 u and \(\mathbf{m}\left({ }_{13}^{28} \mathrm{~A} l\right)\) = 27.98191 u.
Solution:
Q = [m(26Fe56 – 2m (13 Al28.] × 931.5 MeV
= [55.93494 – 2 × 27.9819] × 931.5 MeV
Q = – 0.2886 × 931.5 MeV = – 26.88 MeV
Which is negative.
This fission is not possible energetically.
Question 17.
The fission properties of \({ }_{94}^{239} \mathrm{Pu}\) are very similar to those of \({ }_{92}^{238} U\). The average-energy released per fission is 180 MeV. How much energy, in MeV is released if all the atoms in 1kg of pure \({ }_{94}^{239} \mathrm{Pu}\) undergo fission?
Solution:
No. of atoms in 1kg of pure .
UP = \(\frac{6.023 \times 10^{23}}{239}\) × 1000 = 2.52 × 1024
As average energy released / fission is 180 MeV, therefore total energy released
= 2.52 × 1024 × 180 MeV = 4.53 × 1026 MeV
![]()
Question 18.
A 1000 MW fission reactor consumes half of its fuel In 5.00 y. How much \({ }_{92}^{235} \mathrm{U}\) did it contain initially ? Assume that the reactor operates 80% of the time, that all the energy generated arises from the fission of \({ }_{92}^{235} \mathrm{U}\) and that this nuclide is consumed only by the fission process.
Solution:
In the fission of one nucleus of 92U235 energy generated is 200 MeV
∴ Energy generated in fission of 1 kg of
92U235 = 200 × \(\frac{6 \times 10^{23}}{235}\) × 1000 MeV
= 5.106 × 1026 MeV = 5.106 × 1026 × 1.6 × 10-13J
= 8.17 × 103 J
Time for which reactor operates \(\frac{80}{100}\) × 5
years = 4 years.
Total energy generated in 5 years.
= 1000 × 106 × 60 × 60 × 24 × 365 × 4J
∴ Amount of U consumed in 5 years
= \(\frac{1000 \times 10^6 \times 60 \times 60 \times 24 \times 365 \times 4}{8.17 \times 10^{13}} \mathrm{~kg}\)
= 1544 kg
∴ Initial amount of 92U235 = 2 × 1544 kg
= 3088 kg
Question 19.
How long can an electric lamp. of 100W be kept glowing by fusion of 20 kg of deuterium ? Take the fusion reaction as \({ }_1^2 \mathrm{H}\) + \({ }_1^2 \mathrm{H}\) → \({ }_2^3 \mathrm{He}\) + n + 3.27 MeV
Solution:
Number of deuterium atoms in 2.0 kg
\(\frac{6.023 \times 10^{23} \times 2000}{2}\) = 6.023 × 1026
Energy released when 2 atoms füse = 3.27 MeV
∴ Total energy released
= \(\frac{3.27}{2}\) × 6.023 × 1026 MeV
= 1.635 × 6.023 × 1026 × 1.6 × 10-13 j
= 15.75 × 103 J
Enery consumed by the bulb/sec = 100 J
∴ Time for which bulb will glow
= \(\frac{15.75 \times 10^{13}}{100} \mathrm{~S}\)
= \(\frac{15.75 \times 10^{11}}{60 \times 60 \times 24 \times 365}\) = 4.99 × 107 years
Question 20.
Calculate the height of the potential barrier for a head on collision of two deuterons. (Hint : The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm.
Solution:
For head on collision distance between centres of two deuterons = r = 2 × radius
r = 4 fm = 4 × 10-15 m
Charge of each deuteron e = 1.6 × 10-10 C
Potential energy
\(\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{r}}\) = \(\frac{9 \times 10^9\left(1.6 \times 10^{-19}\right)^2}{4 \times 10^{-15}}\) Joule
= \(\frac{9 \times 1.6 \times 1.6 \times 10^{-14}}{4 \times 1.6 \times 10^{-16}}\)KeV
PE = 360 KeV
P.E = 2 × K.E of each deuteron = 360 KeV
K.E of each deuteron = \(\frac{360}{2}\) = 180 KeV
This is a measure of height of Coulomb barrier
Question 21.
From the relation R = R0A1/3, where R0, is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A.
Solution:
Density of nuclear matter
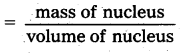
ρ = \(\frac{\mathrm{mA}}{\frac{4}{3} \pi \mathrm{R}^3}\), where m is average mass of a nucleon
Using R = R0A1/3 we get
ρ = \(\frac{3 \mathrm{~mA}}{4 \pi\left(\mathrm{R}_0 \mathrm{~A}^{1 / 3}\right)^3}\) = \(\frac{3 \mathrm{~m}}{4 \pi \mathrm{R}_0^3}\)
As R0 is constant, therefore ρ is constant.
Question 22.
For the β+ (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K – shell, is captured by the nucleus and a neutrino is emitted).
![]()
Show that if β+ emission is energetically allowed, electron capture is necessarily allowed but not vice-versa.
Solution:
The β+ emission from a nucleus ZXA may be represented as
zXA = z-1YA + 1e0 + v + Q1 —– (i)
The other competing process of electron capture may be represented as
-1e0 + ZXA = Z-1yA + v + Q2 —– (ii)
The energy released in Q1 in (1. is given by
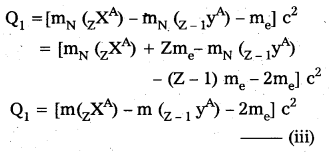
Note that mN here denotes mass of nucleus and m denotes the mass of atom similarly from (ii)
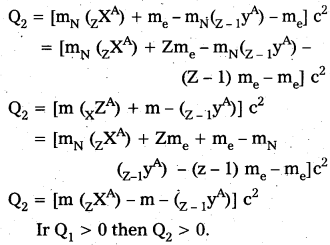
Ir Q1 > 0 then Q2 > 0
i.e., If positron emission is energetically allowed electron capture is necessarily allowed. But Q2 > 0 does not necessarily mean Q1 > 0. Hence the reverse is not true.
Additional Exercises
Question 1.
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are \({ }_{12}^{24} \mathrm{Mg}\) (23.98504u), \({ }_{12}^{25} \mathrm{Mg}\) (24.98584u) and \({ }_{12}^{26} \mathrm{Mg}\) (25.98259u). The natural abundance of \({ }_{12}^{24} \mathrm{Mg}\) is 78.99% by mass. Calculate the abundances of other two isotopes.
Solution:
Let the abundance of \({ }_{12} \mathrm{Mg}^{25}\) by mass be x% therefore, abundance of 12Mg26 by mass
= (100 – 78.99 – x%)
= (21.01 – x%)
Now average atomic mass of magnesium is
24.312 =
\(\frac{23.98504 \times 78.99+24.98584+25.98529(21.01-\mathrm{x})}{100}\)
on solving we get x = 9.303% for 12Mg25 and for 12Mg26 (21.01 – x) = 11.71%
![]()
Question 2.
The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei \({ }_{20}^{41} \mathrm{Ca}\) and \({ }_{13}^{27} \mathbf{Al}\) from the following data: .
m(\({ }_{20}^{40} \mathrm{Ca}\)) = 39.962591 u
m(\({ }_{20}^{41} \mathrm{Ca}\)) = 40.962278 u
m({ }_{13}^{26} \mathrm{Ca}) = 25.986895 u
m({ }_{13}^{27} \mathrm{Ca}) = 26.981541 u
Solution:
When a neutron is separated from 20Ca41 we are left with
20Ca40 i.e. 20Ca41 → 20Ca40 + 0n1
Now mass defect
ΔM = m(20Ca40) + mn – m (20Ca41)
= 39.962591 + 1.008665 – 40.962278
= 0.008978 a.m.u
∴ Neutron seperation energy
= 0.008978 × 931MeV
= 8.362 MeV
similarly 13Al27 → 13Al26 + 0n1
∴ Mass defect, ΔM = m (13Al26) + mn – m(13Al27)
= 25.986895 + 1.008665 – 26.981541
= 0.013845 u
∴ Neutron seperation energy. = 0.0138454 × 931MeV
= 12.89 MeV
Question 3.
A source contains two phosphorous radio nuclides \({ }_{15}^{32} \mathbf{P}\) (T1/2 = 14.3d) and \({ }_{15}^{33} P\) (T1/2 = 25.3d). Initially, 10% of the decays come from \({ }_{15}^{33} \mathrm{P}\). How long one must wait until 90% do so ?
Solution:
Suppose initially the source has 90% 15pt32 and 10% \({ }_{15} \mathrm{P}_{\mathrm{t}}^{32}\), say 9x gram P2 and x gram of P1.
After t days, suppose the source has 90% \({ }_{15} \mathbf{P}_2^{33}\) and 10% \({ }_{15} \mathrm{P}_{\mathrm{t}}^{32}\) i.e., y gram of P2 and 9y gram of P1
we have to calculate :
from \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = \(\left(\frac{1}{2}\right)^n\) = \(\left(\frac{1}{2}\right)^{t / T}\) = 2-i/T
N = N02-t/T
y = 9×2-t/14.3 for P2 and 9y = x 2-t/25.3 for P1
Dividing we get
\(\frac{1}{9}\) = 9 × 2(t/25.3 – t/14.3.)
or \(\frac{1}{81}\) = 2-11t/25.3 × 14.3
log 1 – log 81 = \(\frac{-11 \mathrm{t}}{25.3 \times 14.3}\) log 2
0 – 1 – 9085 = \(\frac{-11 \mathrm{t}}{25.3 \times 14.3}\) × 0.3010.
t = \(\frac{25.3 \times 14.3 \times 1.9085}{11 \times 0.3010}\) = 208.5 days
Question 4.
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α – particle. Consider the following decay processes :
\({ }_{88}^{223} \mathrm{Ra}\) → \({ }_{82}^{209} \mathrm{~Pb}\) + \({ }_6^{14} \mathrm{C}\)
\({ }_{88}^{223} \mathrm{Ra}\) → \({ }_{86}^{219} \mathrm{~Pb}\) + \({ }_2^4 \mathrm{He}\)
Calculate the Q-values for these decays and determine that both are energetically allowed.
Solution:
i) For the decay process
88Ra 223 → 82pb209 + 6C14 + Q
mass defect, ΔM = mass of Ra223 – (mass of pb209 + mass of C14)
= 223.01850 – (208.98107 + 14.00324)
= 0.03419u
Q = 0.03419 × 931 MeV = 31.83 MeV
ii) For the decay process
88Ra23 → 86Rn219 + 2He4 + Q mass defect, ΔM = mass of Ra223 – (mass of Rn219 + mass of He4) = 223.01850 – (219.00948 + 4.00260)
= 0.00642 u
∴ Q = 0.00642 × 931 MeV = 5.98 MeV
As Q values are positive in both the cases, therefore both the decays are energetically possible.
Question 5.
Consider the fission of \({ }_{92}^{238} \mathbf{U}\) by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are \({ }_{58}^{140} \mathrm{Ce}\) and \({ }_{44}^{99} \mathrm{Ru}\). Calculate Q for this fission process. The relevant atomic and particle masses are
m(\({ }_{92}^{238} \mathrm{U}\)) = 238.05079 u
m(\({ }_{58}^{140} \mathrm{Ce}\)) = 139.90543 u
m(\({ }_{44}^{99} \mathrm{Ru}\))= 98.90594 u
Solution:
For this fission reaction,
92U238 + on1 → 58Ce140 + 44Ru99 + Q
mass defect ΔM = mass of U238 + mass of n – (mass of Ce140 + mass of Ru99.
= 238.05079 + 1.00867 – (139.90543 + 98.90594)
= 0.24809U
∴ Q = 0.24809 × 931 MeV = 230.97 Mev
![]()
Question 6.
Consider the D-T reaction (deuterium- tritium fusion)
\({ }_1^2 \mathrm{H}\) + \({ }_1^3 \mathrm{H}\) → \({ }_2^4 \mathrm{He}\) + n
a) Calculate the energy released in MeV in this reaction from the data:
m\(\left({ }_1^2 \mathrm{H}\right)\) = 2.014102 u
m\(\left({ }_1^3 \mathrm{H}\right)\) = 3.016049 u
b) Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the Coulomb repulsion between the two nuclei ? To what temperature must the gas heated to
initiate the reaction ?
(Hint : Kinetic energy required for one fusion event = average thermal kinetic energy available with the interacting particles = 2(3kt/2); k = Boltzman’s constant, T = absolute temperature..
Solution:
a) For the process 1H2 + 1H3 + 2He4 + n + Q
Q = [m(1H2) + m (1H3) + m(2He4) – mn] × 931 MeV
= (2.014102 + 3.016049 – 4.002603
1.00867) × 931 MeV
= 0.018878 × 931 = 17.58 MeV
b) Repulsive potential energy of two nuclei when they almost touch each other is
= \(\frac{q^2}{4 \pi \varepsilon_0(2 r)}\) = \(\frac{9 \times 10^9\left(1.6 \times 10^{-19}\right)^7}{2 \times 2 \times 10^{-15}}\) Joule
= 5.76 × 10-14 Joule
Classically KE atleast equal to this amount is required to overcome Coulomb repulsion. Using the relation
K.E. = 2 × \(\frac{3}{2}\) KT
T = \(\frac{\mathrm{K} \cdot \mathrm{E}}{3 \mathrm{k}}\) = \(\frac{5.76 \times 10^{-14}}{3 \times 1.38 \times 10^{-23}}\) = 1.39 × 109K
In actual practise the temperature required for trigerring the reaction is somewhat less.
Question 7.
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. You are given that
m(198Au) = 197.968233 u
m(198Hg) = 197.966760 u.
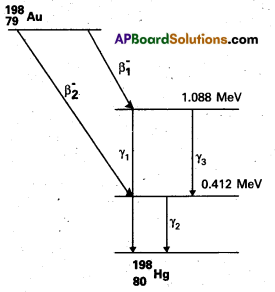
Solution:
Energy corresponding to r1
E1 = 1.088 – 0 = 1.088 MeV
= 1.088 × 1.6 × 10-13 Joule
Frequency v1 = \(\frac{E_1}{h}\)
= \(\frac{1.088 \times 1.6 \times 10^{-13}}{6.6 \times 10^{-34}}\)
= 2.63 × 1020 HZ
similarly v2 = \(\frac{\mathrm{E}_2}{\mathrm{~h}}\)
= \(\frac{0.412 \times 1.6 \times 10^{-12}}{6.6 \times 10^{10}}\)
= 9.98 × 1013 Hz
and v3 = \(\frac{E_3}{h}\)
= \(\frac{(1.088-0.412) \times 1.6 \times 10^{-13}}{6.6 \times 10^{20} \mathrm{~Hz}}\)
Maximum K.E. of β1 particle
Kmax (β1)= [m(79Au198 – mass of Second excited state of 80Hg198] × 931 MeV
= [m(79Au198) – m(82Hg198) – \(\frac{1.088}{931}\)] × 931 MeV
= 931 [197.968233 – 197.966760] – 1.088 MeV
= 1.371 – 1.088 = 0.283 MeV
similarly kmax (β2) – 0.957 MeV
Question 8.
Calculate and compare the energy released by a. fusion of 1.0 kg of hydrogen deep within Sun and b. the fission of 1.0 kg of 235U in a fission reactor.
Solution:
In sun, four hydrogen nuclei fuse to form a helium nucleus with the release of 26 MeV energy.
∴ Energy released by fusion of 1 kg of hydrogen = \(\frac{6 \times 10^{23} \times 26}{4}\) × 103 MeV
As energy released in fission of one atom of 92U236 = 200 MeV
Energy released in fission of 1 kg of 92U238
= \(\frac{6 \times 10^{23} \times 1000}{235}\) × 200 MeV
E2 = 5.1 × 1026 MeV
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}\) = \(\frac{39 \times 10^{26}}{5.1 \times 10^{26}}\) = 7.65
i.e., Energy released in fusion is 7.65 times the energy released in fission.
Question 9.
Suppose India had a target of producing by 2020 AD, 2,00,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i.e. conversion to electric energy of thermal energy produced in a reactór was 25%.
How much amount of fissionable uranium would our country need per year by 2020 ? Take the heat energy per fission of 235U to be about 200 MeV.
Solution:
Total targeted power = 2 × 105 MW
Total Nuclear power = 10% of 2 × 105 MW
= 2 × 104 MW
Energy produced in fission = 200 MeV
Effeciency of power plant =25%
∴ Energy converted into electrical energy per fission = \(\frac{25}{100}\) × 200 = 50 MeV
= 50 × 1.6 × 10-13 Joule.
Total electrical energy to be produced :
= 2 × 104 MW = 2 × 104 × 106 Watt
= 2 × 1010 Joule/Sec
= 2 × 1010 × 60 × 60 × 24 × 365 Joule / year
No. of fissions in one year
= \(\frac{2 \times 10^{10} \times 60 \times 60 \times 24 \times 365}{50 \times 1.6 \times 10^{-13}}\)
= 2 × \(\frac{36 \times 24 \times 365}{8}\) × 1024
Mass of 6.023 × 1023 atoms of U235 = 235 gm = 235 × 10-3 kg
Mass of \(\frac{2 \times 36 \times 24 \times 365}{8}\) × 1024 atoms
= \(\frac{235 \times 10^{-3}}{6.023 \times 10^{23}}\) × \(\frac{2 \times 36 \times 24 \times 365 \times 20^{24}}{8}\)
= 3.08 × 104 Kg
Hence mass of Uranium needed per year = 3.08 × 104 Kg.