AP Inter 2nd Year Physics Study Material Chapter 3 తరంగ దృశాశాస్త్రం

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 3rd Lesson తరంగ దృశాశాస్త్రం Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 3rd Lesson తరంగ దృశాశాస్త్రం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఫ్రెనెల్ దూరం అంటే ఏమిటి?
జవాబు:
సరళరేఖా మార్గం నుండి కాంతి కిరణపుంజం గుర్తించదగ్గ విచలనం చెందేవరకు ప్రయాణించే కనిష్ఠ దూరాన్ని ఫ్రెనెల్ దూరం అంటారు.
ఫ్రెనెల్ దూరం (Z_F) = \(\frac{a^2}{\lambda}\); a = ద్వారం యొక్క మందము; λ = తరంగ దైర్ఘ్యము

ప్రశ్న 2.
కిరణ దృశాశాస్త్రం చెల్లుబాటుకు సమర్ధనను ఇవ్వండి.
జవాబు:
Z_F కన్నా దూరాలు బాగా తక్కువైనప్పుడు, కిరణం యొక్క పరిమాణంతో పోల్చినప్పుడు వివర్తనం వల్ల విస్తరణ తక్కువగా ఉంటుంది.

దూరాలు Z_F కు సమానం మరియు Z_F కన్నా బాగా ఎక్కువైతే వివర్తనం వల్ల విస్తరణ కిరణ దృశాశాస్త్రంలో అధిగమిస్తుంది. (ద్వారం పరిమాణం a).
Z_F = \(\frac{a^2}{\lambda}\)

ఈ సమీకరణం నుండి తరంగదైర్ఘ్య అవధి సున్నాను సమీపిస్తే కిరణ దృశాశాస్త్రము పాటించబడుతుంది.

ప్రశ్న 3.
కాంతి ధృవణం అంటే ఏమిటి?
జవాబు:
కాంతి యొక్క కంపనాలు కేవలం ఒకే ఒక్క దిశలో ఉంటే ఆ దృగ్విషయాన్ని ధ్రువణం అంటారు.
(లేదా)
కాంతి తరంగం యొక్క విద్యుత్ క్షేత్ర తిర్యక్ సదిశ, ఒకే తలానికి పరిమితమైతే ఆదృగ్విషయాన్ని ధ్రువణం అంటారు.

ప్రశ్న 4.
మాలస్ నియమం అంటే ఏమిటి?
జవాబు:
విశ్లేషణకారి గుండా పోయే ప్రసార ధ్రువిత కాంతి యొక్క తీవ్రత, విశ్లేషణకారి యొక్క ప్రసారతలానికి, ధ్రువణకారి యొక్క తలానికి మధ్యగల కొసైన కోణము వర్గానికి అనులోమానుపాతంలో ఉంటుంది.
I cos² θ; I = I₀ cos² θ.

ప్రశ్న 5.
బ్రూస్టర్ నియమాన్ని వివరించండి.
జవాబు:
బ్రూస్టర్ నియమం :
యానకం యొక్క వక్రీభవన గుణకము ధ్రువణ కోణము యొక్క టాంజెట్ విలువకు సమానం.
µ = tan i_B, ఇక్కడ i_B = బ్రూస్టర్ నియమం, µ = వక్రీభవన గుణకం
గమనిక : r + i_B = 90°

ప్రశ్న 6.
ఒక పరావర్తక తలం మీద పతనమైన ఏకవర్ణ కాంతి పుంజం ఎప్పుడు పూర్తిగా ప్రసారితం అవుతుంది?
జవాబు:
లేసర్ జనకం నుండి ఉద్గారమైన కాంతిని ధ్రువణకారి గుండా పంపి, పరావర్తిత తలంపై బ్రూస్టర్ కోణం (i_B) తో పతనమైనప్పుడు ధ్రువణకారిని తిప్పితే ఒక నిర్దిష్ట అమరిక వద్ద పతనకాంతి పూర్తిగా ప్రసారమవుతుంది.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
కాంతిలో డాప్లర్ ప్రభావాన్ని వివరించండి. అరుణ విస్థాపనం, నీలివిస్థాపనాల మధ్య భేదాన్ని గుర్తించండి. [TS (Mar.’16)]
జవాబు:
కాంతితో డాప్లర్ ప్రభావం :
కాంతిజనకము మరియు పరిశీలకుడు మధ్య సాపేక్ష గమనము ఉన్నప్పుడు, కాంతి యొక్క దృశ్య పౌనఃపున్యములో మార్పు జరుగుతుంది. ఈ దృగ్విషయాన్ని డాప్లర్ ప్రభావం అంటారు.

పరిశీలకుడు మరియు కాంతి జనకం మధ్యదూరం తక్కువైతే కాంతి యొక్క దృశ్యపౌనఃపున్యము పెరుగుతుంది. మరియు పరిశీలకుడు, కాంతిజనకం మధ్యదూరం పెరిగితే, కాంతి యొక్క దృశ్యపౌనఃపున్యము తగ్గుతుంది.

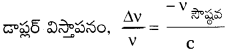
అనువర్తనాలు :

1. దీనిని ఉపయోగించి నక్షత్రాల వేగాన్ని మరియు పాలపుంతల వేగాన్ని కొలవవచ్చు.
2. దీనిని ఉపయోగించి సూర్యుడి భ్రమణవడిని తెలుసుకోవచ్చు.

అరుణ విస్తాపనం :
వర్ణపటంలోని దృగ్గోచర ప్రాంతం యొక్క మధ్యభాగం దృశ్య తరంగదైర్ఘ్యము ఎరుపురంగువైపు కదులుతుంది. దీనిని అరుణ విస్తాపనం అంటారు.

నీలి విస్తాపనం :
జనకం నుండి సేకరించిన తరంగాలు, పరిశీలకుడివైపు చలించినప్పుడు, దృశ్యతరంగదైర్ఘ్యము తగ్గుతుంది. దీనినే నీలివిస్తాపనం అంటారు.

ప్రశ్న 2.
సంపూర్ణాంతర పరావర్తనం అంటే ఏమిటి? ఈ దృగ్విషయాన్ని హైగెన్స్ సూత్రాన్ని ఉపయోగించి పరిశీలించండి.
జవాబు:
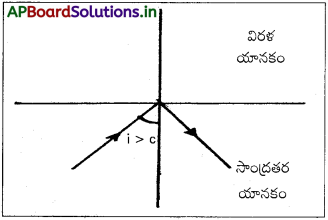
సంపూర్ణాంతర పరావర్తనం :
కాంతికిరణము సాంద్రతర యానకం నుండి విరళయానకంలోకి ప్రయాణించినప్పుడు, పతన కోణం, సందిగ్ధకోణం కన్నా ఎక్కువైతే తిరిగి అదేయానకంలోకి పరావర్తనం చెందుతుంది. ఈ దృగ్విషయాన్ని సంపూర్ణాంతర పరావర్తనం అంటారు.

హైగెన్ సూత్రం :
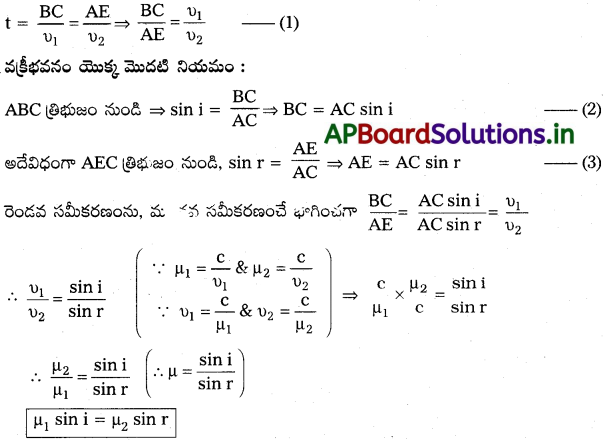
హైగెన్ నియమం ప్రకారం తరంగాగ్రం ABపై ఉన్న ప్రతిబిందువు, గౌణ తరంగాగ్రాలకు జనకం వలే పని చేస్తుంది. తరంగాగ్రముBనుండి Cకి ప్రయాణించుటకు పట్టుకాలము.
దూరం BC = υτ

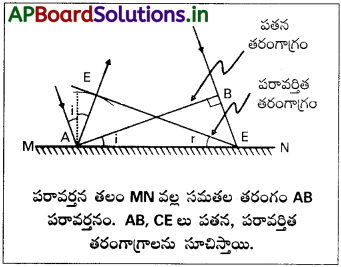
పరావర్తన తరంగాన్ని υτ వ్యాసార్థం గల గోళంగా A బిందువు నుండి గీయాలి.

C నుండి గోళము వరకు ఒక స్పర్శరేఖ CE ని గీయాలి.
AE = BC = υτ

EAC మరియు BAC లు ఒకే మాదిరి త్రిభుజాలు.

∴ i మరియు r కోణాలు సమానం. దీనిని పరావర్తన నియమం అంటారు.

ప్రశ్న 3.
కాంతి వ్యతికరణం సంభవించే బిందువు వద్ద కాంతి తీవ్రతకు సమాసాన్ని ఉత్పాదించండి. గరిష్ట, శూన్య తీవ్రతల నిబంధనలను రాబట్టండి. [AP. Mar.’16; ‘TS. Mar.’15]
జవాబు:
ఒకే కంపన పరిమితి (a) గల రెండు తరంగాల స్థానభ్రంశాలు Y మరియు y2 అనుకొనుము. అనునది వాటి మధ్య దశాభేదం అనుకొనుము.
y₁ = a sin ωt ………………… (1)
y₂ = a sin (ωt + Φ) ……………… (2)
ఫలిత స్థానభ్రంశం y = y₁ + y₂

y = a sin ωt + a sin (ωt + Φ)
y = a sin ωt + a sin ωt cos Φ + a cos ωt sin Φ
y = a sin ωt [1 + cos Φ] + cos ωt (a sin Φ) ………… (3)
R cos θ = a (1 + cos Φ) ………… (4)
R sin θ = a sin Φ ………… (5)
y = R sin ωt . cos θ + R cos ωt . sin θ
y = R sin (ωt + θ) ………….. (6)

ఇక్కడ R అనునది P వద్ద ఫలిత కంపన పరిమితి, (4) మరియు (5) సమీకరణాలను వర్గము చేసి కూడగా
R² [cos² θ + sin² θ] = a²[1 + cos² Φ + 2 cos Φ + sin² Φ]
R² [1] = a’ [1 + 1 + 2 cos Φ]

ప్రశ్న 4.
వ్యతికరణం, వివర్తనం’ దృగ్విషయాలకు శక్తి నిత్యత్వ నియమం వర్తిస్తుందా? క్లుప్తంగా వివరించండి. [Mar. ’14]
జవాబు:
అవును. శక్తి నిత్యత్వ నియమం పాటించబడుతుంది. నిర్మాణాత్మక వ్యతికరణములో తీవ్రత గరిష్ఠం. కాబట్టి వెలుగు పట్టీలు తెరపై ఏర్పడతాయి. అదేవిధంగా వినాశాత్మక వ్యతికరణము జరిగినప్పుడు తీవ్రత కనిష్ఠం. కాబట్టి తెరపై చీకటి పట్టీలు ఏర్పడతాయి.

ఈ విధంగా ఏర్పడిన వ్యతికరణము మరియు వివర్తనంలో కాంతి తీవ్రత తిరిగి సర్దుబాటు జరుగుతుంది. అనగా శక్తి ద్యుతిహీన పట్టీ (చీకటి పట్టీ) నుండి ద్యుతిమయ పట్టీ (వెలుగుపట్టీ)కి బదిలీ జరుగుతుంది. ఇక్కడ శక్తి సృష్టించబడలేదు (లేదా) నాశనం చేయబడలేదు. కేవలం పునఃసర్దుబాటు జరిగింది.

కాబట్టి వ్యతికరణము మరియు వివర్తనాలలో శక్తి నిత్యత్వ నియమం పాటించబడుతుంది.

ప్రశ్న 5.
మీ కన్ను పృథక్కరణ సామర్థ్యాన్ని మీరు ఏ విధంగా నిర్థారిస్తారు? [AP Mar.’17]
జవాబు:
సమాన వెడల్పు గల నలుపు నిలువు చారలను వాటితో విడివడిన తెలుపు చారలను తయారు చేయండి. అన్ని నలుపు నిలువు చారలు సమాన వెడల్పు కలిగి ఉండాలి. అయితే వాటిమధ్య మధ్యస్థంగా తెలుపు నిలువుచారల వెడల్పు ఎడమ నుండి కుడికి పోయేకొద్ది పెరుగుతూ పోవాలి.

ఇప్పుడు ఉత్తమంగా ఒక కంటితో మాత్రమే వ్యూహాన్ని వీక్షించండి. గోడ నుండి దూరంగా (లేదా) దగ్గరగా చలించడం’ ద్వారా, మీరు ఏవైనా రెండు మాత్రమే నలుపు నిలువు చారలను వేరుపడిన చారలుగా కనిపించే స్థానాన్ని గుర్తించండి.

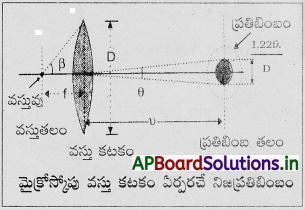
ఈ నలుపు చారకు ఎడమవైపుకు ఉండే అన్ని నిలువు చారలు ఒకదానితో ఒకటి కలిసిపోయి, భేదపరచడానికి వీలుగాకుండా అవుతాయి. మరోవైపు దీనికి కుడివైపున ఉండే నలుపుచారలు మరింత స్పష్టంగా దృగ్గోచరమవుతాయి.

రెండు ప్రాంతాలను వేరుచేసే ఆ తెలుపు చార వెడల్పు d ని నమోదు చేసి, మీ కంటి నుండి గోడదూరం D ని కొలవండి. అప్పుడు \(\frac{d}{D}\) అనేదే మైక్రోస్కోపు వస్తు కటకం ఏర్పరచే నిజప్రతిబింబంమీకన్ను యొక్క పృథక్కరణం అవుతుంది.

ప్రశ్న 6.
వ్యత్యస్థంగా ఉండే రెండు పోలరాయిడ్ల మధ్య ఇంకా పోలరాయిడ్ పలకను భ్రమణం చెందించినప్పుడు ప్రసారిత కాంతి తీవ్రతను చర్చించండి. [TS Mar. 17]
జవాబు:
మొదటి ధ్రువణకారి P₁ గుండా పోయిన తర్వాత ధ్రువితకాంతి తీవ్రత I₀ అనుకొనుము. రెండవ ధ్రువణకారి P₂ గుండా పోయిన తర్వాత ధ్రువిత కాంతి తీవ్రత I = I₀cos²θ.

θ అనునది P₁ మరియు P₂ ల అక్షాల మధ్యకోణం. P₁ మరియు P₂ లు లంబంగా ఉన్నప్పుడు P₂ మరియు P₃ మధ్య కోణము (\(\frac{2 \pi}{2}\) – θ)
కాబట్టి P₃ నుండి బహిర్గతమయ్యే కాంతి యొక్క తీవ్రత

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
హైగెన్స్ సూత్రం అంటే ఏమిటి? హైగెన్స్ సూత్రాన్ని ఉపయోగించి వక్రీభవన దృశా దృగ్విషయాన్ని వివరించండి.
జవాబు:
హైగెన్స్ సూత్రం :
తరంగాగ్రం మీద ప్రతి బిందువును కొత్త గౌణజనకంగా తీసుకోవచ్చు.

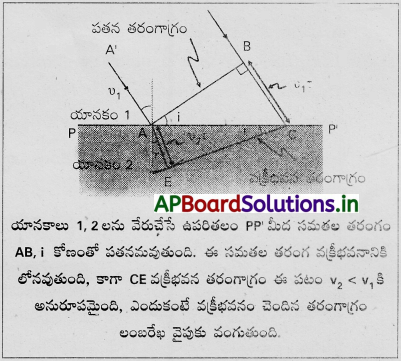
సమతలం నుంచి సమతల తరంగాగ్రం వక్రీభవనం :
PP’ అనే సమతలము µ₁ మరియు µ₂ వక్రీభవన గుణకాలు గల రెండుయానకాలను వేరు చేస్తుంది. మొదటి యానకంలో కాంతి వేగము υ₁ మరియు రెండవ యానకంలో కాంతివేగము υ₂ అనుకొనుము.

హైగెన్ సిద్ధాంతం ప్రకారం పతన తరంగాగ్రం AB పై ప్రతిబిందువు గౌణ జనకంగా తీసుకోవచ్చు. తరంగాగ్రం B నుండి Cని చేరేకాలంలో, తరంగాగ్రం A నుండి E కి చేరుతుంది. B నుండి C కి చేరే కాలము, A నుండి D కి చేరే కాలం t కి సమానం అనుకొనుము.

ఇది స్నెల్ వక్రీభవన నియమం

రెండవ వక్రీభవ నియమం :
పతన కిరణం, పతన బిందువు వద్ద వక్రీభవన తలం PP’ కి గీసిన లంబం, వక్రీభవన కిరణం ఒకే తలంలో ఉన్నాయని రేఖా గణితపరంగా తెలుస్తుంది. ఇది వక్రీభవన నియమాలలో రెండవది.

ప్రశ్న 2.
సంబద్ధం, అసంబద్ధ తరంగాల సంకలనాల మధ్య భేదాన్ని గుర్తించండి. సంపోషక, వినాశాత్మక వ్యతికరణాల సిద్ధాంతాన్ని అభివృద్ధిపరచండి.
జవాబు:
సంబద్ధ జనకాలు :
రెండు జనకాల మధ్య దశాభేదము శూన్య (లేదా) స్థిర దశాభేదం ఉంటే వాటిని సంబద్ధ జనకాలు అంటారు.

అసంబద్ధ జనకాలు :
రెండు జనకాల మధ్య దశాభేదం కాలంతో పాటు మారితే వాటిని అసంబద్ధ జనకాలు అంటారు.

నిర్మాణాత్మక మరియు వినాశాత్మక వ్యతికరణం సిద్ధాంతం :
రెండు సంబద్ధ జనకాల తరంగాలు
y₁ = a sin ωt ………………… (1)
y₂ = a sin (ωt + Φ) ……………… (2)

ఇక్కడ a కంపన పరిమితి, Φ అనునది రెండు తరంగాల మధ్య దశాభేదం.
అధ్యారోపణ సూత్రం ప్రకారం, y = y₁ + y₂.
y = a sin ωt + a sin (ωt + Φ)
= a sin ωt + a sin ωt cos Φ + a cos ωt sin Φ
y = a sin ωt [1 + cos Φ] + cos ωt [a sin Φ] ……………… (3)
A cos θ = a (1 + cos Φ] ……………… (4)
A sin θ = a sin Φ ……………… (5)
(4) మరియు (5) సమీకరణాలను (3)వ సమీకరణంలో ప్రతిక్షేపించగా
y = A sin ωt. cos θ + A cos ωt sin θ
y = A sin (ωt + θ) ………….. (6)
A అనునది ఫలితం కంపన పరిమితి. (4) మరియు (5) సమీకరణాలను వర్గము వేసి కూడగా
A²[cos² θ + sin² θ] = a²[1 + cos² Φ + 2 cos Φ + sin² Φ]
A² [1] = a² [1 + 1 + 2 cos Φ]
I = A² = 2a² [1 + cos Φ] (∵ I = A²)
I = 2a² × 2 cos² \(\frac{\phi}{2}\)
I = 4a2 cos2 1 = 41 cos2 (∵ I₀ = a²)

సందర్భం (i) నిర్మాణాత్మక వ్యతికరణము : తీవ్రత గరిష్ఠం కావాలంటే cos \(\frac{\phi}{2}\) = 1 ⇒ Φ = 2nπ కావాలి.
ఇక్కడ n = 0, 1, 2, 3 … ⇒ Φ = 0, 2π, 4π, 6π ………….. I_{గరిష్ట} 4I₀

సందర్భం (ii) వినాశాత్మక వ్యతికరణము : తీవ్రత కనిష్ఠం కావాలంటే cos Φ = 0 ⇒ Φ = (2n + 1)π
ఇక్కడ n = 0, 1, 2, 3 …………; ⇒ Φ = π, 3π, 5π ⇒ I_{కనిష్ఠం} = 0

ప్రశ్న 3.
వ్యతికరణాన్ని పరిశీలించడానికి యంగ్ ప్రయోగాన్ని వర్ణించండి. దీని నుంచి పట్టీ వెడల్పుకు సమీకరణాన్ని రాబట్టండి.
జవాబు:
వ్యతికరణము :
రెండు (లేదా) అంతకు ఎక్కువ సంఖ్యలో తరంగాలు అధ్యారోపణం చెందడం వల్ల శక్తి తీవ్రతలో సంభవించే మార్పును వ్యతికరణం అంటారు.

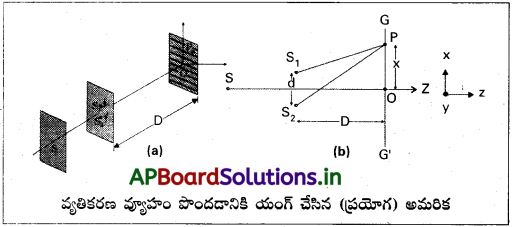
వర్ణన :

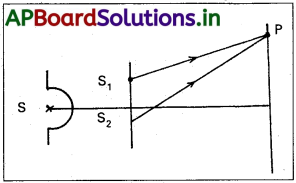
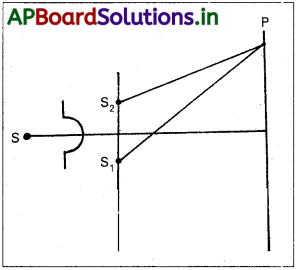
1. థామస్ యంగ్ రెండు సంబద్ధ కాంతి జనకాలను ఉపయోగించి కాంతి వ్యతికరణాన్ని ప్రయోగపూర్వకంగా పరిశీలించాడు.
2. ఏకవర్ణ కాంతి సన్నని సూదిరంధ్రము S పై పతనం చెంది, గోళాకార తరంగాన్ని జనింపచేస్తుంది.
3. S నుండి సమాన దూరాలలో S, మరియు S అను రెండు సన్నని సూది రంధ్రాలు.
4. తెర D దూరంలో ఉంచబడినది.
5. రెండు శృంగాలు (లేదా) రెండు ద్రోణులు అధ్యారోపణం చెందే బిందువుల వద్ద నిర్మాణాత్మక వ్యతికరణము జరిగి తెరపై ద్యుతిమయ పట్టీలు (వెలుగు పట్టీలు) ఏర్పడతాయి.
6. ఒక తరంగము యొక్క శృంగము, మరొక తరంగద్రోణి అధ్యారోపణం చెందే బిందువుల వద్ద వినాశాత్మక వ్యతికరణం జరిగి తెరపై ద్యుతిహీన పట్టీలు (చీకటి పట్టీలు) ఏర్పడతాయి.
7. కాబట్టి తెరపై వెలుగు మరియు చీకటి పట్టీలు ఒకదాని తర్వాత మరొకటి వరుసగా ఏర్పడతాయి.

పట్టీ వెడల్పు :
i) రెండు వరుస వెలుగు. (లేదా) చీకటి పట్టీల మధ్య దూరాన్ని పట్టీ వెడల్పు అంటారు. దీనిని β తో సూచిస్తారు.

ii) పథ భేదం (δ) = d sin θ
θ చాలా స్వల్పమైతే, పటం నుండి sin θ ≈ tan θ = \(\frac{x}{D}\)

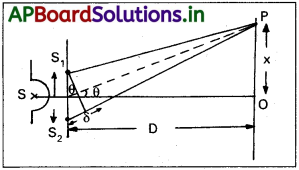
iii) వెలుగు పట్టీల మధ్య పదభేదం S₂P – S₂P = nλ
∴ d sin θ = nλ
d × \(\frac{x}{D}\) = ηλ ; x = \(\frac{n \lambda D}{d}\) ………… (1)
ఇక్కడ n = 0, 1, 2, 3 ……..
ఈ సమీకరణము వెలుగు పట్టీ స్థానాన్ని తెలుపుతుంది.
n = 0, అయితే x₀ = 0

కాబట్టి వెలుగు మరియు చీకటి పట్టీలకు పట్టీ వెడల్పు ఒకేవిధంగా ఉంటుంది.

ప్రశ్న 4.
వివర్తనం అంటే ఏమిటి? ఒంటి చీలిక నుంచి పొందగలిగే వివర్తన వ్యూహాన్ని చర్చించండి.
జవాబు:
వివర్తనం :
అవరోధాల అంచుల వద్ద కాంతి వంగి, జ్యామితీయ ఛాయా ప్రదేశంలోకి వ్యాపిస్తుంది. ఈ దృగ్విషయాన్ని వివర్తనం అంటారు.

ఉదాహరణ:
సూర్యోదయానికి కొద్దిసేపటికి ముందు, పర్వత శిఖరాలు వెండిపొరవలె మెరుస్తాయి.

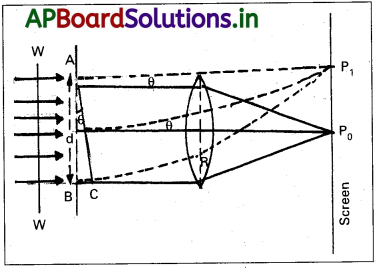
ఏకచీలిక వద్ద కాంతి వివర్తనము:

1. AB అనునది d మందం గల సన్నిని చీలిక. దీనిపై λ తరంగదైర్ఘ్యము గల ఏకవర్ణకాంతి లంబంగా పతనం చెందుచున్నది.
2. వివర్తనం చెందిన కాంతి కుంభాకార కటకం ద్వారా తెరపై కేంద్రీకరణ చెందును.
3. గౌణ తరంగాగ్రములు OP₀ దిశ ప్రయాణించి P₀ వద్ద కేంద్రీకరణ చెందుతాయి.
4. తరంగాగ్రమునకు లంబదిశలో θ కోణము చేయు దిశలో వివర్తనము చెందిన కాంతి P₁ బిందువు వద్ద తెరపై కేంద్రీకరణ చెందినది.
5. P₁ వద్ద తీవ్రతను కనుక్కోవడానికి BR పై AC లంబాన్ని గీయాలి.
6. గౌణ తరంగాగ్రముల మధ్య పథ భేదము BC = AB sin θ = a sin θ (∵ sin θ ≈ θ)
   పథ భేదము (λ) = a θ ………… (1)
7. ప్రయోగ పరిశీలనల ద్వారా పటంలో θ = 0° వద్ద గరిష్ట తీవ్రత, θ = (n + \(\frac{1}{2}\))\(\frac{\lambda}{a}\) వద్ద గౌణ గరిష్ఠములు మరియు θ = \(\frac{n\lambda}{a}\) వద్ద కనిష్ఠ తీవ్రత వచ్చును.
8. (1)వ సమీకరణం నుండి, θ = \(\frac{\lambda}{a}\) ఇప్పుడు చీలికను రెండు సమభాగాలుగా, ప్రతిభాగం \(\frac{a}{2\times}\) పరిమాణం ఉండునట్లు విభజించాలి.
9. θ = \(\frac{n\lambda}{a}\) వద్ద తీవ్రతలు సున్నా అని చూపవచ్చు.
   ఇక్కడ n = 1, 2, 3 ….
10. θ = (n + \(\frac{1}{2}\))\(\frac{\lambda}{a}\) వద్ద కూడా గరిష్టాలు వస్తాయని చూపవచ్చు.
11. θ = \(\frac{3\lambda}{2a}\) అనునది రెండు చీకటి పట్టీల మధ్య మధ్య బిందువు అనుకొనుము.
12. చీలిక యొక్క మొదటి \(\frac{2}{3}\) వంతు తీసుకుంటే, రెండు చివరల మధ్య పదబేధము
    \(\frac{2}{3}\)a × θ = \(\frac{2a}{3}\times\frac{3\lambda}{2a}\) = λ ………. (2)
    
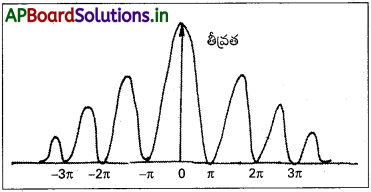
13. చీలిక యొక్క మొదటి \(\frac{2}{3}\) వంతును \(\frac{\lambda}{2}\) పధబేధం ఉండునట్లుగా రెండు భాగాలుగా విభజిస్తే, వీటిలో తీవ్రత రద్దవుతుంది. కేవలం మిగిలిన \(\frac{1}{3}\) వంతు భాగంలో మాత్రమే తీవ్రత కనిష్ఠం.

ప్రశ్న 5.
దృక్ సాధనాల పృథక్కరణ సామర్థ్యం అంటే ఏమిటి? ఏ నిబంధన క్రింద ప్రతిబింబాలు పృథక్కరింపబడతాయో ఉత్పాదించండి.
జవాబు:
పృథక్కరణ సామర్థ్యము :
దగ్గరగా ఉన్న రెండు బిందువులను ఎంతదూరం వరకు విడగొట్టి చూపగలదో ఆ ధారుడ్యాన్ని కటకం యొక్క పృథక్కరణ సామర్థ్యం అంటారు.

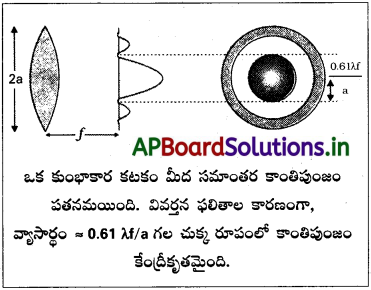
దృశా పరికరాల యొక్క పృథక్కరణ సామర్థ్యము :
i) ఒక సమాంతర కాంతి కిరణము కుంభాకార కటకంపై పతనం చెందినది అనుకొనుము. వివర్తన ప్రభావముచేత, కిరణము పరిమిత వైశాల్యములో చుక్కవలె ఏర్పడుతుంది. ii) వివర్తన ప్రభావాన్ని పరిగణలోకి తీసుకుంటే, మధ్యభాగం వృత్తాకారంగా వెలుగు ప్రాంతం, దాని చుట్టూ చీకటి మరియు వెలుగు వృత్తాలు ఏర్పడతాయి.
iii) కేంద్రము వద్ద వెలుగు ప్రాంతం వ్యాసార్ధము

ఇక్కడ f అనునది కటకం నాభ్యాంతరము 2 = కటకం యొక్క వ్యాసము.

పృథక్కరణకు నిబంధనను రాబట్టుట :
చుక్క పరిమాణము చాలా చిన్నదైతే, పృథక్కరణమునకు గల అవధి చాలా ప్రముఖ పాత్ర పోషిస్తుంది.

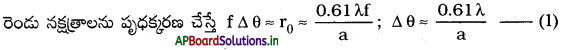
∆θ స్వల్పమైతే, వస్తువు యొక్క వ్యాసము (2a) పెద్దదిగా ఉంటుంది. a విలువ అధికమైతే పృథక్కరణ సామర్థ్యానికి దూరదర్శిని ఉత్తమం.

వస్తువు మరియు వస్తు కటకానికి మధ్య కనిష్ట దూరము d_{కనిష్టం} = \(\frac{1.22 \lambda}{2 \mu \sin \beta}\)

ఇక్కడ µ = వక్రీభవన గుణకం; µ sin B = న్యూమరికల్ అపర్చర్ (సంఖ్యాత్మక కంత)

అభ్యాసాలు Textual Exercises

ప్రశ్న 1.
589 pm తరంగదైర్ఘ్యం గల ఏకవర్ణ కాంతి గాలిలో నుంచి నీటి ఉపరితలంపై పతనమైంది. నీటి వక్రీభవన గుణకం 1.33 అయితే, (a) పరావర్తిత కాంతి, (b) వక్రీభవనం చెందిన కాంతి తరంగదైర్ఘ్యం, పౌనఃపున్యం, వడులను కనుక్కోండి.
సాధన:
λ = 589 nm = 589 × 10^-9 m

a) పరావర్తన కాంతి :
(పతనకాంతి వలే ఒకే తరంగదైర్ఘ్యం, పౌనఃపున్యం, వడి కలిగి ఉంది)
λ = 589 × 10^-9 m, υ = 5.09 × 10¹⁴ Hz

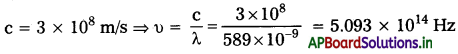
b) వక్రీభవన కాంతి :
(ప్రతన కాంతి వలే ఒకే పౌనఃపున్యం కలిగి ఉంది)
υ = 5.093 × 10¹⁴ Hz

ప్రశ్న 2.
క్రింది ప్రతి సందర్భంలోను తరంగాగ్రం ఆకారం ఏమిటి?
a) ఒక బిందు జనకం నుంచి అపసరం చెందే కాంతి.
b) ఒక కుంభాకార కటకం నాభి వద్ద బిందు జనకాన్ని ఉంచినప్పుడు కటకం నుంచి బహిర్గతమయ్యే కాంతి.
c) భూమి అడ్డగించే సుదూర నక్షత్రం నుంచి వచ్చే కాంతి తరంగాగ్ర భాగం.
సాధన:
a) ఇది గోళాకార తరంగాగ్రం
b) ఇది సమతల తరంగాగ్రం
c) సమతల తరంగాగ్రం (అతిపెద్ద గోళంపై స్వల్ప వైశాల్యం దాదాపు సమతలంగా ఉంటుంది).

ప్రశ్న 3.
a) గాజు వక్రీభవన గుణకం 1.5. గాజులో కాంతి వడి ఎంత? (శూన్యంలో కాంతి వడి 3.0 × 10¹⁴ m s^-1)
b) గాజులో కాంతి వేగం కాంతి రంగు మీద ఆధారపడదా? అలా కాకుంటే, ఎరుపు, ఊదా రెండు రంగులలో ఏది గాజు పట్టకంలో నెమ్మదిగా ప్రయాణిస్తుంది?
సాధన:

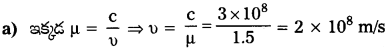
b) లేదు. వక్రీభవన గుణకం మరియు యానకంలో కాంతివేగం తరంగదైర్ఘ్యంపై ఆధారపడును. µ_ν > µ_r.
∴ v_ఊదా < v_{ఎరుపు} కాబట్టి ఊదారంగు కాంతి ఎరుపురంగు కాంతి కన్నా నెమ్మదిగా ప్రయాణిస్తుంది.

ప్రశ్న 4.
యంగ్ జంట చీలిక ప్రయోగంలో, చీలికలను 0.28 mm వేరుపరచి, తెరను 1.4 m దూరంగా ఉంచారు. కేంద్రీయ గరిష్ఠం, నాల్గవ గరిష్ఠాల మధ్య దూరాన్ని 1.2 cm గా కొలిచారు. ప్రయోగంలో ఉపయోగించిన కాంతి తరంగదైర్ఘ్యాన్ని కురుక్కోండి.
సాధన:
d = 0.28 mm = 0.28 × 10^-3 m, D = 1.4 m, β = 1.2 × 10^-2 m, n = 4

ప్రశ్న 5.
ఏకవర్ణ కాంతి తరంగదైర్ఘ్యం λ ని ఉపయోగించిన యంగ్ జంట చీలిక ప్రయోగంలో తెరమీద పథభేదం λ గల ఒక బిందువు వద్ద కాంతి తీవ్రత K యూనిట్లు. పథభేదం λ/3 గల బిందువు వద్ద కాంతి తీవ్రత ఎంత?
సాధన:
I₁ = I₂ = I అనుకొనుము. రెండు కాంతి తరంగాల మధ్య దశాభేదం Φ అయితే ఫలిత తీవ్రత
I_R = I₁ + I₂ + \(2\sqrt{I_1I_2}\) . cos Φ
పథ భేదం = λ, దశాభేదం Φ = 0°
∴ I_R = I + I + \(2\sqrt{II}\) . cos 0° = 4I = k
పథ భేదం = \(\frac{\lambda}{3}\)
దశాభేదం Φ = \(\frac{2 \pi}{3}\) రేడియన్
∴ I’_R = I + I + \(2\sqrt{II}\) . cos \(\frac{2 \pi}{3}\)
⇒ I’_R = 2I + 2I(\(\frac{-1}{2}\)) ⇒ I = \(\frac{k}{4}\)

ప్రశ్న 6.
యంగ్ జంట చీలిక ప్రయోగంలో వ్యతికరణ పట్టీలను పొందడానికి 650nm, 520 nm అనే రెండు తరంగదైర్ఘ్యాలను కలిగి ఉండే ఒక కాంతి పుంజం ఉపయోగిస్తున్నారు.
a) 650 nm తరంగదైర్ఘ్యానికి తెరమీద కేంద్రీయ గరిష్ఠం నుంచి మూడవ ద్యుతిమయ పట్టీకి గల దూరాన్ని కనుక్కోండి.
b) ఈ రెండు తరంగ దైర్ఘ్యాల వల్ల మృతిమయ పట్టీలు ఎక్కడయితే ఏకీభవిస్తాయో అక్కడి నుంచి కేంద్రీయ గరిష్టానికి ఉండే కనీస దూరం ఎంత?
సాధన:
λ₁ = 650nm = 650 × 10^-9m ⇒ λ₂ = 520 nm = 520 × 10^-9 m
d = చీలికల మధ్యదూరం; D = చీలికల నుండి తెరవకు దూరం
a) మూడవ వెలుగు పట్టీ, n = 3 = x = nλ, \(\frac{D}{d}\) = 3 × 650 \(\frac{D}{d}\) nm

b) nవ వెలుగు పట్టీకి λ₂ = 520 nm, (n – 1) వెలుగు పట్టీకి λ₁ = 650nm
∴ nλ₂ = (n- 1) λ₁; n× 520 = (n-1) 650;
4n = 5n – 5 (లేదా) n = 5
∴ అవసరమైన కనిష్ట దూరం, x = nλ₂ \(\frac{D}{d}\) = 5 × 520 \(\frac{D}{d}\) = 2600 \(\frac{D}{d}\)nm.

ప్రశ్న 7.
జంట చీలిక ప్రయోగంలో 1 m దూరంలో ఉంచిన తెరమీద ఒక పట్టీ కోణీయ వెడల్పు 0.2° లుగా కనుక్కోవడమైంది. ఉపయోగించిన కాంతి తరంగదైర్ఘ్యం 600 nm. మొత్తం ప్రయోగ అమరికను కనుక నీటిలో ముంచినట్లయితే పట్టీ కోణీయ వెడల్పు ఎంత ? నీటి వక్రీభవన గుణకాన్ని 4/3 గా తీసుకోండి.
సాధన:
ఇక్కడ θ₁ = 0.2°, D = 1m, λ₁ = 600 nm, θ₂ = ?, µ = 4/3

ప్రశ్న 8.
గాలి నుంచి గాజు సంక్రమణకు బ్రూస్టర్ కోణం ఎంత? (గాజు వక్రీభవన గుణకం = 1.5.)
సాధన:
ఇక్కడ i_p = ? µ = 1.5; tan i_p = µ = 1.5 ∴ i_p = tan^-1 (1.5); i_p = 56.3

ప్రశ్న 9.
5000 తరంగదైర్ఘ్యం గల కాంతి ఒక సమతల పరావర్తక తలం మీద పడింది. పరావర్తిత కాంతి తరంగదైర్ఘ్యం, పౌనః పున్యాలు ఏమిటి? ఏ పతన కోణం విలువకు పరావర్తిత కిరణం, పతన కిరణానికి లంబంగా ఉంటుంది?
సాధన:
λ = 5000 Å = 5 × 10^-7 m
పరావర్తన కాంతి తరంగదైర్ఘ్యం మరియు పౌనఃపున్యం ఒకేవిధంగా ఉంది.
∴ పరావర్తన కాంతి తరంగదైర్ఘ్యం (λ) = 5000 Å

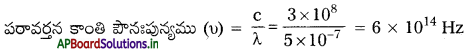
పతన కోణం i = 45° అయితే పరావర్తన కాంతి, పతనకాంతికి లంబంగా ఉంటుంది.

ప్రశ్న 10.
4 mm కంత, 400 nm కాంతి తరంగదైర్ఘ్యం ఉంటే కిరణ దృశాశాస్త్రం ఎంత దూరానికి సరియైన ఉజ్జాయింపు చేయబడుతుందో అంచనా వేయండి.
సాధన:
a = 4 mm = 4 × 10^-3 m; 1 = 400nm = 400 × 10^-9 m = 4 × 10^-7 m
కిరణ దృశా శాస్త్రంలో దూరాలు, ఫైనల్ దూరాలకు దాదాపుగా సమానం

అదనపు అభ్యాసాలు Additional Exercises

ప్రశ్న 11.
ఒక నక్షత్రంలోని హైడ్రోజన్ వల్ల ఉద్గారమైన 6563 Å Hα రేఖ 15 Åలకు అరుణ విస్థాపనం చెందినట్లు గుర్తించారు. నక్షత్రం ఎంత-వడితో భూమి నుంచి దూరంగా వెళుతున్నదో అంచనా వేయండి.
సాధన:
λ’ = λ = 15Å = 15 × 10^-10m; λ = 6563 Å = 6563 × 10^-10 m; v = ?

ప్రశ్న 12.
శూన్యంలో కాంతివేగం కంటే ఏదైనా ఒక యానకంలో, (నీరు అనుకోండి) కాంతివేగం ఎక్కువగా ఉంటుందని కాంతి కణమయ సిద్ధాంతం ఏవిధంగా ప్రాగుక్తీకరిస్తుందో వివరించండి. నీటిలో కాంతి వేగాన్ని కనుక్కొనే ప్రాయోగిక నిర్ధారణ వల్ల ఈ ప్రాగుక్తీకరణ ధృవపరచబడ్డదా? అలాకాకపోతే, ప్రయోగంలో ఏ ప్రత్యామ్నాయ కాంతి చిత్రణ సుసంగతంగా ఉంటుంది?
సాధన:
న్యూటన్ కణ సిద్ధాంతం ప్రకారం వక్రీభవనంలో విరళ యానకం నుండి వచ్చే పతన కాంతి కిరణాలలోని కణాలు సాంద్రతర యానకంలో కన్నా, తలానికి లంబంగా ఆకర్షణ బలాన్ని కలిగిస్తాయి.
దీని ఫలితంగా లంబవేగాంశము పెరుగుతుంది. కాని తలం వెంబడి అంశం మారదు.

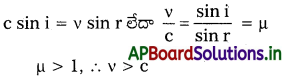
ప్రయోగఫలితాలకు ఇది విరుద్ధం (V > c). కావున కాంతి తరంగస్వభావం కలిగి ఉంది.

ప్రశ్న 13.
హైగెన్స్ సూత్రం ఏవిధంగా పరావర్తన, వక్రీభవన నియమాలకు దారితీసిందో ఈ పాఠ్యాంశంలో మీరు నేర్చుకొన్నారు. ఇదే సూత్రాన్ని నేరుగా ఉపయోగించి; ఒక సమతల దర్పణం ముందు ఒక బిందు జనకాన్ని ఉంచినప్పుడు దర్పణం నుంచి దాని మిధ్యా ప్రతిబింబ దూరం, దర్పణం నుంచి వస్తుదూరానికి సమానమని ఉత్పాదించండి.
సాధన:

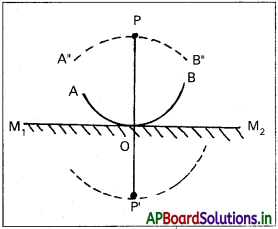
పటంలో సమతల దర్పణం M₁ M₂ నుండి దూరంలో ఒక బిందురూప వస్తువు P. OP = r = వ్యాసార్థం గోళాకార చాపాన్ని (AB) గీయాలి. ఇది వస్తువు నుండి గోళాకార తరంగాగ్రం. ఇది M₁ M₂ పై పతనమవుతుంది. దర్పణం లేకపోతే A’B’ తరంగాగ్రం స్థానం A’B’ అవుతుంది. ఇక్కడ PP’ = 2r, దర్పణం ఉండుటచే AB తరంగాగ్రం A”PB”ను తెలుపుతుంది. హైగెన్ నిర్మాణం ప్రకారం పటంలో A’B’ మరియు A”B” అను రెండు గోళాకార తరంగాగ్రాలు దర్పణం M₁ M₂ కు ఇరువైపులా సౌష్టవంగా ఉన్నాయి. A’PB’ అనునది A”PB” యొక్క పరావర్తన ప్రతిబింబం. కావున జ్యామితీయంగా OP OP’ అని నిరూపించబడినది.

ప్రశ్న 14.
తరంగ ప్రసార వడిని ప్రభావితం చేయ సాధ్యమయ్యే కొన్ని అంశాలను పేర్కొందాం :
i) జనక స్వభావం ii) ప్రసార దిశ iii) జనకం మరియు / లేదా పరిశీలకుని చలనం iv) తరంగదైర్ఘ v) తరంగ తీవ్రత
క్రింది ఏ అంశాలపై, ఒకవేళ ఏదైనా, ఆధారపడుతుందా?
a) శూన్యంలో కాంతి వేగం,
b) యానకం (గాజు లేదా నీరు అనుకోండి)లో కాంతి వేగం.
సాధన:
a) శూన్యంలో కాంతివేగం విశ్వస్థిరాంకం, మిగిలిన అన్ని అంశాలపై ఆధారపడదు.

b) యానకంలో కాంతి వేగంపై ఆధారపడును.
i) జనకం యొక్క స్వభావంపై ఆధారపడదు.
ii) యానకంలో ప్రసార దిశపై ఆధారపడదు.
iii) యానకంతో సాపేక్షంగా జనకం చలనంపై ఆధారపడదు. కాని యానకంలో సాపేక్షంగా పరిశీలకుడి చలనంపై ఆధారపడుతుంది.
iv) తరంగదైర్ఘ్యంపై ఆధారపడుతుంది.
v) తీవ్రతపై ఆధారపడదు.

ప్రశ్న 15.
ధ్వని తరంగాల సందర్భానికి పౌనఃపున్య విస్థాపనానికి డాప్లర్ ఫార్ములా రెండు పరిస్థితుల మధ్య స్వల్పంగా తేడా కలిగి ఉంటుంది : (i) జనకం విరామంలో ఉండి; పరిశీలకుడు కదులుతున్నప్పుడు, (ii) జనకం చలిస్తున్నప్పుడు; పరిశీలకుడు నిశ్చలంగా ఉన్నప్పుడు. అయితే, శూన్యంలో ప్రయాణించే కాంతి తరంగాల సందర్భానికి యధాతథ డాప్లర్ ఫార్ములాలు, ఈ పరిస్థితులకు ఖచ్చితంగా సర్వసమానం. ఈ విధంగా ఎందుకు ఉండాలో వివరించండి. ఇవే రెండు పరిస్థితులకు, ఒక యానకంలో కాంతి ప్రయాణిస్తున్నప్పుడు కూడా ఫార్ములాలు ఖచ్చితంగా సర్వసమానంగా ఉంటాయని మీరు ఆశిస్తారా?
సాధన:
ధ్వని ప్రసారానికి యానకం అవసరం. అందువలన (i) మరియు (ii) సందర్భాలలో జనకం మరియు పరిశీలకుడు మధ్య సాపేక్ష గమనంలో ఉన్నప్పుడు ఒకే విధంగా ఉండదు. రెండు సందర్భాలలో యానకంతో పరిశీలకుడు సాపేక్ష. గమనంలో ఉన్నప్పుడు, డాప్లర్ సూత్రం వేరువేరుగా ఉంటుంది.

కాంతి శూన్యంలో ప్రయాణిస్తున్నప్పుడు, రెండు సందర్భాలలో తేడాను గుర్తించలేం. కావున సూత్రాలు ఖచ్చితంగా సమానం.

కాంతి యానకంలో ప్రయాణిస్తున్నప్పుడు (i) మరియు (ii) సందర్భాలు సమానం కాదు. కావున సూత్రాలు కూడా వేరువేరుగా ఉంటాయి.

ప్రశ్న 16.
600nm తరంగదైర్ఘ్యం ఉపయోగించే యంగ్ జంట చీలిక ప్రయోగంలో, దూరంగా ఉన్న తెరపై ఏర్పడిన పట్టీ కోణీయ వెడల్పు 0.1°. రెండు చీలికల మధ్య ఉండే అంతరం ఎంత?
సాధన:
λ = 600 nm = 6 × 10^-7 m,

ప్రశ్న 17.
క్రింది ప్రశ్నలకు సమాధానాలివ్వండి :
a) ఒంటి చీలిక వివర్తన ప్రయోగంలో చీలిక వెడల్పును మౌలిక (original) వెడల్పుకు రెండు రెట్లు చేశారు. కేంద్రీయ వివర్తన పట్టీ పరిమాణం, తీవ్రతలను ఇది ఏవిధంగా ప్రభావితం చేస్తుంది?
b) జంట చీలిక ప్రయోగంలోని వ్యతికరణ వ్యూహంతో ఒక్కో చీలిక వల్ల కలిగే వివర్తనం ఏవిధంగా సంబంధాన్ని కలిగి ఉంటుంది?
c) సుదూర జనకం నుంచి వచ్చే కాంతి మార్గంలో చాలా చిన్నదైన ఒక వృత్తాకార అడ్డును ఉంచినప్పుడు అడ్డు జ్యామితీయ ఛాయ కేంద్రం వద్ద ఒక ద్యుతిమయ చుక్కను చూడటమైంది. ఎందుకో వివరించండి.
d) 10 m ఎత్తుగల ఒక గదిలో ఇద్దరు విద్యార్థులు విభజన గోడ (separated wall) తో 7 m వేరు చేసి ఉన్నారు. కాంతి, ధ్వని తరంగాలు రెండూ అడ్డుల చుట్టూతా వంగగలిగినా వాళ్ళిద్దరూ మాట్లాడుకోవడం సులభం. కానీ ఒకరినొకరు చూసుకోవడం ఎందుకు సాధ్యపడదు?
e) కాంతి సరళరేఖా మార్గంలో ప్రయాణిస్తుందనే ఊహన మీద కిరణ దృశాశాస్త్రం ఆధారపడి ఉన్నది. కానీ వివర్తన ప్రభావాలు (చిన్నవి కంత / చీలికలు లేదా చిన్న అడ్డుల చుట్టూతా కాంతి ప్రసారమైనప్పుడు పరిశీలించినది) ఈ ఊహనను తప్పు అని నిరూపిస్తున్నాయి. అయినా కూడా, దృక్సాధనాల విషయంలో ప్రతిబింబాల స్థానాలను, ఇతరత్రా ధర్మాలను అర్థం చేసుకోవడంలో కిరణ దృశాశాస్త్రం భావనలను చాలా సాధారణంగా ఉపయోగిస్తారు. దీనికి మీ సమర్ధన ఏమిటి?
సాధన:
a) ప్రకారం, కేంద్ర వివర్తన పట్టీ పరిమాణం సగానికి క్షీణిస్తే తీవ్రత నాలుగు రెట్లు పెరుగుతుంది.

b) జంట చీలికల ప్రయోగంలో వ్యతికరణ పట్టీల యొక్క తీవ్రతను, ప్రతి చీలిక యొక్క వివర్తనంతో మాడ్యులేట్ చేయవచ్చు.

c) వృత్తాకార అడ్డు యొక్క అంచు వద్ద వివర్తనం చెందిన తరంగం, జ్యామితీయ ప్రాంతం యొక్క కేంద్రం వద్ద వెలుగు పట్టీని ఏర్పరుస్తుంది.

d) వివర్తనంలో అడ్డు యొక్క పరిమాణం, కాంతి తరంగదైర్ఘ్యం కన్నా తక్కువగా ఉంటుంది. అనుకోకుండా అడ్డు యొక్క పరిమాణం తరంగదైర్ఘ్యం కన్నా బాగా ఎక్కువైతే స్వల్ప కోణం వివర్తనం జరుగును. అడ్డుగోడ యొక్క పరిమాణం కొన్ని మీటర్లు ఉంటుంది. కాంతి యొక్క తరంగదైర్ఘ్యం 5 × 10^-7 m, ధ్వని 1 kHZ పౌనఃపున్యము వద్ద ‘తరంగదైర్ఘ్యం 0.3 m. అందువలన ధ్వని తరంగాలు వంగుతాయి కాని కాంతి తరంగాలు వంగవు.

e) సాధారణ దృశా పరికరాల పరిమాణము తరంగదైర్ఘ్యం కన్నా అధికం.

ప్రశ్న 18.
రెండు కొండల పైభాగంలో ఉన్న రెండు శిఖరాలు (towers) 40 km ఎడంతో ఉన్నాయి. వీటిని కలిపే రేఖ రెండు శిఖరాలకు మధ్య సగభాగంలో ఒక కొండకు 50 m పైన పోతున్నది. గుర్తించగల వివర్తన ఫలితాలు లేకుండా శిఖరాల మధ్య పంపించగలిగే రేడియో తరంగాల అత్యంత దీర్ఘ (longest) తరంగదైర్ఘ్యం ఎంత?
సాధన:

ప్రశ్న 19.
500nm తరంగదైర్ఘ్యం గల ఒక సమాంతర కాంతి పుంజం ఒక సన్నని చీలిక మీద పడుతుంది. ఫలిత వివర్తన వ్యూహం 1 m దూరంగా ఉండే తెరపై పరిశీలించడమైంది. తెర యొక్క కేంద్రం నుంచి మొదటి కనిష్ఠం 2.5mm దూరం వద్ద గమనించారు. చీలిక వెడల్పును కనుక్కోండి.
సాధన:
λ = 500 nm = 5 × 10^-7 m, D = 1 m, y = 2.5 mm = 2.5 × 10^-3 m, d = ?

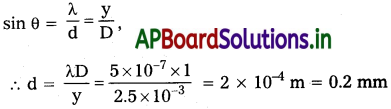
ప్రశ్న 20.
క్రింది ప్రశ్నలకు సమాధానాలివ్వండి :
a) తక్కువ ఎత్తులో ఎగిరే ఎయిర్ క్రాప్ట్ పైనుంచి వెళ్లినప్పుడు మన టి.వి. తెరపై బొమ్మ కొద్దిగా కదులుతున్నట్లు మనం గమనిస్తాం. దీనికి సాధ్యమయ్యే వివరణను సూచించండి.
b) వివర్తన, వ్యతికరణ వ్యూహాలలో తీవ్రత వితరణలను అవగాహన చేసుకోవడంలో తరంగ స్థానభ్రంశాల రేఖీయ అధ్యారోపణ సూత్రం ప్రాథమికమైనదని మీరు పాఠ్యాంశంలో నేర్చుకొన్నారు. ఈ సూత్రాన్ని ఏ విధంగా మీరు సమర్థిస్తారు?
సాధన:
a) యాంటెన్నా గ్రహించే సంకేతం, ఎయిర్ క్రాప్ట్ నుండి పరావర్తనం చెందే బలహీన సంకేతంతో వ్యతికరణం చెందుతుంది.

b) తరంగ చలనంలో సమీకరణము అధ్యారోపణ సూత్రాన్ని పాటిస్తుంది. ఇది నిజం, తరంగ కణాలు స్వల్ప కంపన పరిమితి కలిగి ఉంటాయి.

ప్రశ్న 21.
ఒంటి చీలిక వివర్త వ్యూహం ఉత్పాదనలో nλ/a కోణాల వద్ద తీవ్రత శూన్యమని చెప్పడమైంది. చీలికను సరియైన విధంగా విభజించడం ద్వారా రద్దుపరచే భావనను సమర్ధించండి.
సాధన:
చీలికను n చీలికలుగా విభజిస్తే చీలిక మందం a’ = \(\frac{a}{n}\). θ దిశలో ప్రతి చిన్న చీలిక తీవ్రత సున్నా. అందువల్ల మొత్తం తీవ్రత సున్నా

సాధించిన సమస్యలు Textual Examples

ప్రశ్న 1.
589.0 mm తరంగదైర్ఘ్యం వద్ద ఉండే సోడియం రేఖ 589.6 pm వద్ద ఉన్నట్లు పరిశీలించినట్లయితే మనకు సాపేక్షంగా పాలపుంత ఎంత వడితో చలించాలి?
సాధన:
νλ = C కాబట్టి, \(\frac{\Delta v}{v}=-\frac{\Delta \lambda}{\lambda}\)
(ν, λ గెలలో స్వల్ప మార్పులకు)
∆λ = 589.6 – 589.0 = + 0.6nm
క్రింది సమీకరణంను ఉపయోగించినట్లయితే,

కాబట్టి, పాలపుంత మన నుంచి దూరంగా చలిస్తోంది.

ప్రశ్న 2.
a) రెండు యానకాలను వేరుచేసే తలం మీద ఏకవర్ణ కాంతి పడినప్పుడు, పరావర్తనం, వక్రీభవనం చెందిన కాంతులు రెండూ పతన పౌనఃపున్యంతో సమానంగా పౌనఃపున్యాన్ని కలిగి ఉన్నాయి. ఎందుకో వివరించండి.
b) కాంతి విరళయానకం నుంచి సాంద్రతర యానకంలోకి ప్రయాణించినప్పుడు కాంతి వడి తగ్గుతుంది. వడిలో తగ్గుదల కాంతి తరంగం మోసుకొనిపోయే శక్తిలో తగ్గుదలను సూచిస్తుందా?
c) కాంతి తరంగ చిత్రణలో కాంతి తీవ్రతను కంపనపరిమితి వర్గంతో నిర్ధారిస్తారు. మరి కాంతి ఫోటాన్ చిత్రణలో ఏది కాంతి తీవ్రతను నిర్ధారిస్తుంది.
సాధన:
a) ద్రవ్య పరమాణువులు ఆంగికాలతో పతనకాంతి జరిపే అన్యోన్య చర్య వల్ల పరావర్తనం, వక్రీభవనాలు ఉద్భవిస్తాయి. పరమాణువులను డోలకాలుగా చూడవచ్చు. ఇవి, బాహ్య కారకం పౌనఃపున్యాన్ని తీసుకొని బలాత్కృత డోలనాలు చేస్తాయి. ఆవేశితమైన డోలకం నుంచి ఉద్గారమయ్యే కాంతి పౌనఃపున్యం దాని డోలన పౌనఃపున్యానికి సమానం. కాబట్టి, పరిక్షిప్త కాంతి పౌనఃపున్యం పతన కాంతి పౌనఃపున్యానికి సమానంగా ఉంటుంది.

b) లేదు. ఒక తరంగం మోసుకొనిపోయే శక్తి దాని కంపనపరిమితి మీద ఆధారపడి ఉంటుంది. అంతేగాని తరంగ ప్రసార వడి మీద కాదు.

c) ఫోటాన్ చిత్రణలో, ఇచ్చిన పౌనఃపున్యానికి, ఏకాంక వైశాల్యాన్ని ఏకాంక కాలంలో దాటిపోయే ఫోటాన్ల సంఖ్యతో కాంతి తీవ్రతను నిర్ధారిస్తారు.

ప్రశ్న 3.
1 mm ఎడంతో రెండు చీలికలను చేసి తెరను 1m దూరంలో ఉంచారు. ఉపయోగించిన నీలం-ఆకుపచ్చ కాంతి తరంగదైర్ఘ్యం 500 nm అయితే పట్టీ అంతరం ఎంత?
జవాబు:

ప్రశ్న 4.
క్రింది ఒక్కొక్క పరిక్రియలవల్ల యంగ్ జంట చీలిక ప్రయోగంలో వ్యతికరణ పట్టీల మీద ఎటువంటి ప్రభావం ఉంటుంది?
a) చీలికల తలం నుంచి తెరను దూరంగా జరిపితే ;
b) (ఏకవర్ణ) జనకం బదులు హ్రస్వ తరంగదైర్ఘ్యం గల మరొక (ఏకవర్ణ) జనకాన్ని ఉపయోగిస్తే;
c) చీలికల మధ్య అంతరం పెరిగితే;
d) జనకం చీలికను జంట చీలిక తలానికి దగ్గరగా జరిపితే;
e) జనకం చీలిక వెడల్పు పెరిగితే;
f) ఏకవర్ణ కాంతి జనకం బదులు వేరొక తెల్లని కాంతి జనకాన్ని ఉపయోగిస్తే
(ప్రతి ఒక్కో పరిక్రియలో నిర్దేశించినవి మినహా, అన్ని పరామితులు మారకుండా ఉంటాయి.)
జవాబు:
a) పట్టీల కోణీయ అంతరం (= λd) స్థిరంగా ఉంటుంది. చీలికల తలం నుంచి తెరకు గల దూరానికి అనులోమానుపాతంగా పట్టీల వాస్తవ అంతరం పెరుగుతుంది.