AP Inter 2nd Year Physics Study Material Chapter 9 విద్యుదయస్కాంత ప్రేరణ

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 9th Lesson విద్యుదయస్కాంత ప్రేరణ Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 9th Lesson విద్యుదయస్కాంత ప్రేరణ

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఫారడే, హెన్రీ చేసిన ప్రయోగాలు ఏమి నిరూపించాయి?
జవాబు:
ఫారడే మరియు హెన్రీ అనేక ప్రయోగాల ఆధారంగా విద్యుదయస్కాంత ప్రేరణ ఆవిష్కరణ మరియు అర్థం చేసుకోవడం జరిగింది.

ప్రశ్న 2.
అయస్కాంత అభివాహాన్ని నిర్వచించండి.
జవాబు:
ఒక తలం నుండి పోయే మొత్తం అయస్కాంత బలరేఖల సంఖ్యను అయస్కాంత అభివాహం అంటారు.
Φ_B = \(\overrightarrow{B}.\overrightarrow{AB}\) = BA cos θ
C.G.S ప్రమాణం → మాక్స్వెల్
S.I. ప్రమాణం → వెబర్ (wb)
అయస్కాంత అభివాహం అదిశరాశి.

ప్రశ్న 3.
ఫారడే విద్యుదయస్కాంత ప్రేరణ నియమాన్ని తెలపండి.
జవాబు:
ప్రేరిత విద్యుచ్ఛాలక బలం పరిమాణం, అయస్కాంత అభివాహంలో మార్పు రేటుకు అనులోమానుపాతంలో ఉంటుంది.
ε ∝ \(\frac{-\mathrm{d} \phi}{\mathrm{dt}}\)

ప్రశ్న 4.
లెంజ్ నియమాన్ని తెలపండి.
జవాబు:
ప్రేరిత విద్యుచ్ఛాలక బలదిశ ఎప్పుడూ దాన్ని కలగచేసిన అయస్కాంత క్షేత్ర అభివాహం మార్పును వ్యతిరేకిస్తుంది. ఈ నియమాన్ని లెంజ్ నియమం అంటారు.

ప్రశ్న 5.
ఏకరీతి అయస్కాంత క్షేత్రంలో వాహకాన్ని కదిలించినప్పుడు యాంత్రిక శక్తి (చలనం యొక్క) ఏమౌతుంది?
జవాబు:
అయస్కాంత క్షేత్రంలో వాహకం చలనం వల్ల చలన విద్యుచ్ఛాలక బలం జనిస్తుంది.
చలన వి.చా.బ (ε) = Blυ.

ప్రశ్న 6.
ఎడ్డీ విద్యుత్ ప్రవాహాలు అంటే ఏమిటి? [AP. Mar. ’15]
జవాబు:
ఎడ్డీ విద్యుత్ ప్రవాహాలు లేదా ఫోకాల్టు ప్రవాహాలు:
వాహకాలను మారుతున్న అయస్కాంత అభివాహానికి గురిచేసినప్పుడు, వాటిలో ప్రేరిత విద్యుత్ ప్రవాహాలు ఉత్పన్నమవుతాయి. ఈ సుళ్ళు తిరిగే విద్యుత్ ప్రవాహాలను ఎడ్డీ ప్రవాహాలు అంటారు. ఎడ్డీ ప్రవాహాల వల్ల ఉష్ణరూపంలో శక్తి నష్టం జరుగుతుంది.

ప్రశ్న 7.
ప్రేరకత్వాన్ని నిర్వచించండి.
జవాబు:
ప్రేరకత్వం అనునది విద్యుదయస్కాంత ప్రేరణ గుణకం. ఇది కెపాసిటెన్స్ వలె పదార్థం యొక్క స్వతస్సిద్ధ ధర్మం. ప్రేరకత్వం అనునది అదిశరాశి. ఇది తీగచుట్ట జ్యామితిపైన ఆధారపడుతుంది.

ప్రశ్న 8.
‘స్వయం ప్రేరకత్వం’ అంటే మీరు ఏమి అర్ధం చేసుకొన్నారు?
జవాబు:
ఒక తీగచుట్టలో విద్యుత్ ప్రవాహంలో మార్పు రేటు ఏకాంక విలువ అయితే, దానిలో జనించే ప్రేరిత విద్యుచ్ఛాలక బలాన్ని స్వయం ప్రేరకత అంటారు.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
గమన తలానికి లంబంగా ఉన్న ఏకరీతి అయస్కాంత క్షేత్రంలో విద్యుత్ వాహకం చలించినప్పుడు వాహకం కొనల మధ్య ప్రేరితమయ్యే విద్యుచ్ఛాలక బలానికి సమాసాన్ని పొందండి.
జవాబు:

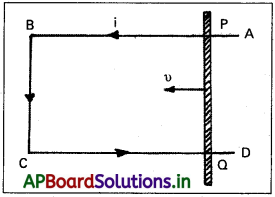
దీర్ఘ చతురస్రాకార వాహకం ABCD పై l పొడవు గల PQ వాహకం \(\overrightarrow{B}\) ఏకరీతి అయస్కాంత క్షేత్రంలో υ ఏకరీతి వేగంలో స్వేచ్ఛగా చలిస్తోందనుకొనుము. ఏదైనా అనియత ఆవేశము q వాహకంలో అదే వేగంతో క్షేత్రంలో చలిస్తోందనుకొనుము.
ఈ ఆవేశంపై లారెంజ్ బలం
(F) = Bqυ ……….. (1)
P నుండి Qకు ఆవేశము చలించుటకు జరిగిన పని
W = బలం × స్థానభ్రంశం
W = Bqυ × l (2) (బలం దిశ ఫ్లెమింగ్ ఎడమచేతి నియమం ఆధారంగా చూపబడుతుంది.)
చలనాత్మక విద్యుచ్ఛాలక బలం (ε) = \(\frac{w}{q}\)
ε = \(\frac{Bqυl}{q}\)
చలనాత్మక విద్యుచ్ఛాలక బలం (ε) = Blυ.

ప్రశ్న 2.
ఎడ్డీ విద్యుత్ ప్రవాహాలను లాభదాయకంగా ఎన్ని విధాలుగా ఉపయోగించవచ్చో వర్ణించండి. [AP. Mar.’17; AP. Mar: ’16; AP & TS. Mar.’15]
జవాబు:
i) రైళ్ళలో అయస్కాంత బ్రేకులు :
విద్యుత్ సామర్థ్యంతో నడిచే కొన్ని రైళ్ళలో, వాటిలోని ఇనుప కమ్మీలపైన ప్రబల విద్యుదయస్కాంతాలను అమరుస్తారు. ఈ విద్యుదయస్కాంతాలు చర్యలోకి రాగానే, ఆ ఇనుప కమ్మీలలో ప్రేరితమయ్యే ఎడ్డీ ప్రవాహాలు రైలు చలనాన్ని వ్యతిరేకిస్తాయి. కాబట్టి రైలు ఆగిపోవడం అనే ప్రభావం మృదువుగా జరుగుతుంది.

ii) ప్రేరణ మోటార్ :
షార్ట్ సర్క్యూట్ చేసిన రోటర్ను ఎడ్డీ విద్యుత్ ప్రవాహాలు తిప్పుతాయి. సీలింగ్ ఫ్యాన్ కూడా ప్రేరణ మోటార్. ఇది ఒకే దశ ఏకాంతర విద్యుత్ ప్రవాహంలో పనిచేస్తుంది.

iii) విద్యుదయస్కాంత అవరుద్ధం :
కొన్ని గాల్వనీ మాపకాలలో అయస్కాంతీయ లోహ పదార్థంతో తయారయిన ఒక కోర్ బిగించి ఉంటుంది. ఇందులోని తీగచుట్ట డోలనాలు చేసినప్పుడు ఆ కోర్లో ఉత్పత్తి అయ్యే ఎడ్డీ ప్రవాహాలు దాని చలనాన్ని వ్యతిరేకించి, వెంటనే తీగచుట్టను విరామస్థితికి తీసుకొస్తాయి.

iv) ప్రేరణ కొలిమి :
అత్యధిక ఉష్ణోగ్రతలను ఉత్పత్తి చేయడానికి ప్రేరణ’ కొలిమిని ఉపయోగించవచ్చు. ఈ ఉష్ణోగ్రతలను వాడుకోవడం ద్వారా అంశిక భాగాలుగా ఉన్న లోహాలను కరిగించి మిశ్రమ లోహాలను తయారుచేయవచ్చు. కరిగించవలసిన లోహాలను ఆవృతం చేసే తీగచుట్ట ద్వారా అధిక పౌనఃపున్యం గల ఏకాంతర విద్యుత్ ప్రవాహాన్ని పంపిస్తారు. అప్పుడు ఆ లోహాలలో జనించే ఎడ్డీ ప్రవాహాలు ఆ లోహాలను కరిగించే ఉష్ణోగ్రతలను ఉత్పత్తి చేస్తాయి.

v) విద్యుత్ సామర్థ్య మీటర్లు :
మన ఇళ్ళలో వాడే అనలాగ్ మీటర్లలోని మెరిసే లోహపు బిళ్ళ ఎడ్డీ ప్రవాహాల వల్లనే భ్రమిస్తూ ఉంటుంది. ఒక తీగచుట్టలో జ్యావక్రీయంగా మారే ప్రవాహాలు ఉత్పత్తి చేస్తే అయస్కాంత క్షేత్రాలు ఈ బిళ్ళలో విద్యుత్ ప్రవాహాలను ప్రేరేపిస్తాయి. ఈ విధంగా తిరుగుతున్న మెరిసే బిళ్ళను మీ ఇంట్లోని సామర్థ్య మీటర్లో గమనించవచ్చు.

ప్రశ్న 3.
రెండు పొడవైన సహాక్ష సాలినాయిడ్ల అన్యోన్య ప్రేరకత్వానికి ఒక సమాసాన్ని పొందండి.
జవాబు:

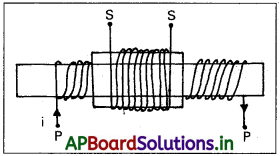
పటంలో రెండు సాలినాయిడ్లను చూడవచ్చు. ప్రాథమిక చుట్ట పొడవు l మరియు అడ్డుకోత వైశాల్యం A అనుకొనుము. N₁ మరియు N₂లు ప్రాథమిక, గౌణ చుట్టలలో చుట్ల సంఖ్య n₁ మరియు n₂లు. ప్రమాణ పొడవులలో చుట్లసంఖ్య [n₁ = \(\frac{N_1}{l}\) మరియు n₂ = \(\frac{N_2}{l}\)]. ప్రాథమిక తీగచుట్టలో విద్యుత్ ప్రవాహం i అనుకొనుము.
ప్రాథమిక తీగచుట్టలో అయస్కాంత ప్రేరణ (B) = µ₀n₁ I = \(\frac{\mu_0 \mathbf{N}_1 \mathrm{I}}{l}\) …………. (1)
ప్రాథమిక తీగచుట్టలో ప్రతి చుట్ట గుండా అయస్కాంత అభివాహం

ప్రశ్న 4.
అయస్కాంత క్షేత్రం, సాలినాయిడ్ వైశాల్యం, పొడవు పదాలలో సాలినాయిడ్లో నిల్వ ఉండే అయస్కాంత శక్తికి ఒక సమాసాన్ని పొందండి.
జవాబు:
L ప్రేరకత గల ప్రేరకం గుండా విద్యుత్ ప్రవహిస్తే, దానిలో ప్రేరిత విద్యుచ్ఛాలక బలం
ε = -L \(\frac{dI}{dt}\)dI ………….. (1)
(ఇక్కడ ఋణ గుర్తు వి.చా. బ., విద్యుత్ ప్రవాహాన్ని వ్యతిరేకిస్తుంది.)

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఫారడే, హెన్రీలు చేసిన అసాధారణ ప్రయోగాలను సంగ్రహంగా వివరించి, విద్యుదయస్కాంతత్వాన్ని అర్థం చేసుకోవడంలో ఈ ప్రయోగాలు చేసిన అంశదానాల ప్రాధాన్యతను ఇవ్వండి.
జవాబు:
ఫారడే మరియు హెన్రీ ప్రయోగాలు :

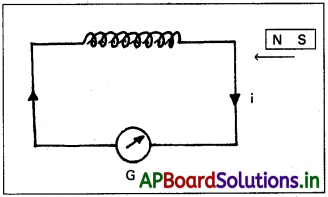
ప్రయోగం 1:
సాపేక్ష చలనం వల్ల అయస్కాంతం విద్యుత్ ప్రవాహాన్ని ప్రేరేపిస్తుంది.

1. పరికరంలో తీగచుట్టకు గాల్వనామీటరు G కలుపబడి ఉంటుంది మరియు దండాయస్కాంతము ఉంటుంది.
2. దండాయస్కాంతం (NS) నిశ్చలంగా ఉన్నప్పుడు, గాల్వనా మీటరులో అపవర్తనం ఉండదు.
3. దండాయస్కాంతం యొక్క ఉత్తర ధృవాన్ని తీగచుట్టవైపు జరిపితే వలయంలో ప్రేరిత విద్యుత్ ప్రవహించి, గాల్వనామీటరులో ఒకవైపు అపవర్తనం కలుగుతుంది.
4. దండాయస్కాంతం యొక్క ఉత్తర ధృవాన్ని, తీగచుట్ట నుండి దూరంగా జరిపితే వలయంలో ప్రేరిత విద్యుత్ ప్రవహించి, గాల్వనామీటరులో ఇప్పుడు వ్యతిరేక దిశలో అపవర్తనం కలుగుతుంది.
5. దండాయస్కాంతంను తీగచుట్టకు దగ్గరగా (లేదా) దూరంగా వేగంగా జరిపితే గాల్వనామీటరులో అపవర్తనం ఎక్కువగా ఉంటుంది.
6. దండాయస్కాంతం దక్షిణ ధ్రువాన్ని తీగచుట్టకు దగ్గరగా (లేదా) దూరంగా జరిపితే గాల్వనామీటరులో అపవర్తనం ఉత్తర ధ్రువంలో వచ్చు అపవర్తనానికి వ్యతిరేక దిశలో ఉంటుంది.

దీనిని బట్టి తీగచుట్టకు, అయస్కాంత క్షేత్రానికి మధ్య సాపేక్షవేగం ఉన్నప్పుడు మాత్రమే విద్యుచ్ఛాలకు బలం ప్రేరితమవుతుంది. అయస్కాంతం మరియు తీగచుట్టకు మధ్య సాపేక్ష చలనం అధికంగా ఉంటే ప్రేరిత వి.చా.బ (లేదా) విద్యుత్ అధికంగా జనిస్తుంది.

ప్రయోగం 2:
తీగచుట్ల మధ్య సాపేక్ష గమనం వల్ల ప్రేరిత విద్యుత్ జనించుట :

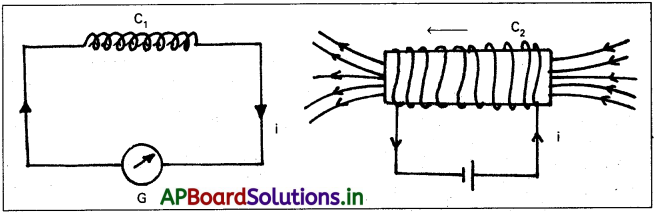
1. దండాయస్కాంతంను తీసివేసి బ్యాటరీ కలిపిన గౌణ తీగచుట్ట C₂ ను పటంలో చూడండి.
2. తీగచుట్టలో C₂ లో స్థిర విద్యుత్ ప్రవాహము స్థిర అయస్కాంత క్షేత్రాన్ని ఏర్పరుస్తుంది.
3. C₂ తీగచుట్టను C₁ తీగచుట్ట వైపు జరిపితే, గాల్వనామీటరు అపవర్తనాన్ని చూపుతుంది. తీగచుట్ట C₁ లో విద్యుత్ ప్రవాహం ప్రేరితమవుతుందని ఇది సూచిస్తుంది.
4. C₂ తీగచుట్టను దూరంగా జరిపితే గాల్వనా మీటరులో వ్యతిరేక దిశలో అపవర్తనం కలుగుతుంది.
5. C₂ తీగచుట్ట చలనంలో ఉన్నంతసేపు అపవర్తనం చూపుతుంది.
6. C₂ తీగచుట్టను స్థిరంగా ఉంచి, C₁ ని కదిల్చినా ఒకే విధమైన ప్రభావాన్ని చూడవచ్చు.

ప్రయోగం 3 :
సాపేక్ష చలనం లేకుండా మారే విద్యుత్ ప్రవాహం, విద్యుత్ ప్రవాహాన్ని ప్రేరేపిస్తుంది :

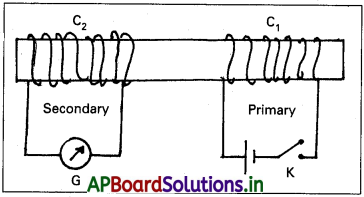
1. ఫారడే ప్రయోగం ద్వారా సాపేక్ష గమనం తప్పనిసరి కాదని నిరూపించాడు.
2. పటంలో C₁ మరియు C₂ తీగచుట్టలు నిశ్చలంగా ఉన్నాయి.
3. C₁ తీగచుట్టకు ట్యాప్ కీ Kతో బ్యాటరీని కలుపుతారు మరియు C₂ తీగచుట్టకు గాల్వనా మీటరును కలుపుతారు.
4. ట్యాప్ కీని నొక్కినప్పుడు గాల్వనా మీటరులో అపవర్తనం కలుగుతుంది.
5. గాల్వనామీటరులో సూచీ ఆకస్మికంగా తిరిగి సున్నాను చూపుతుంది.
6. ట్యాప్ కీని అవిచ్ఛిన్నంగా మూసి ఉంచితే, గాల్వనా మీటరులో అపవర్తనం కలుగదు.
7. ట్యాప్ కీని వదిలితే, గాల్వనా మీటరులో వ్యతిరేక దిశలో అపవర్తనం కలుగుతుంది.
8. కొయ్య కాండానికి బదులు ఇనుప కడ్డీని ఉపయోగించినప్పుడు, విద్యుత్ ప్రవాహ పరిమాణం పెరుగుతుంది.

ప్రశ్న 2.
ఏకాంతర విద్యుత్ ప్రవాహ జనరేటర్ సాధనం పనితీరును సరళమైన పటం, అవసరమైన సమాసాల సహాయంతో వర్ణించండి.
జవాబు:
యాంత్రికశక్తిని విద్యుత్ శక్తిగా మార్చే విద్యుత్ యంత్రాన్ని AC జనరేటర్ (లేదా) ఆల్టర్నేటర్ అంటారు.

సూత్రం :
ఇది విద్యుదయస్కాంత ప్రేరణపై పనిచేస్తుంది.

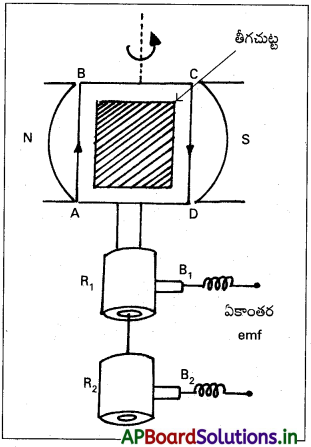
నిర్మాణం :
i) ఆర్మేచర్ :
మెత్తని ఇనుపకోర్పై బంధిత రాగితీగను అనేక చుట్లుగా చుట్టబడిన ABCD ని ఆర్మేచర్ తీగచుట్ట అంటారు.

ii) బలమైన అయస్కాంతం :
బలమైన శాశ్వత అయస్కాంతం (లేదా) విద్యుదయస్కాంత ధ్రువాలు N మరియు S స్థూపాకారంగా ఉంటాయి. ఇది బలమైన క్షేత్ర అయస్కాంతంగా ఉపయోగపడుతుంది. అయస్కాంత ధ్రువాల మధ్య ఆర్మేచర్ తీగచుట్ట తిరుగుతుంది.

iii) స్లిప్ రింగ్లు :
ఆర్మేచర్ తీగచుట్ట రెండు చివరలకు రెండు ఇత్తడి స్లిపింగ్లు R₁ మరియు R₂ లు కలుపబడి ఉంటాయి. ఈ స్లిప్ రింగ్లు ఆర్మేచర్ దిశలో తిరుగుతాయి.

iv) బ్రష్లు :
B₁ మరియు B₂ అను రెండు కార్బన్ బ్రష్ లు స్లిపింగ్లను నొక్కుతాయి. బ్రష్లు స్థిరంగా ఉంటాయి, కాని స్లిపింగ్లు ఆర్మేచర్ తిరిగే దిశలో తిరుగుతాయి. ఈ బ్రష్ల నుండి పొందిన నిర్గమనాన్ని లోడ్కు కలుపుతారు.

పనిచేయు విధానం :
ABCD ఆర్మేచర్ తీగచుట్ట అయస్కాంత క్షేత్రంలో తిరిగితే బలమైన అయస్కాంత క్షేత్రాన్ని అందిస్తుంది. ఇది అయస్కాంత బలరేఖలను ఖండిస్తుంది. ఆర్మేచర్ భ్రమణం వల్ల తీగచుట్టలో అయస్కాంత అభివాహం మారుతుంది. అందువలన తీగచుట్టలో విద్యుచ్చాలకు జలం ప్రేరితమవుతుంది.

అర్థ భ్రమణానికి బ్రష్ B₁ ద్వారా ఒక దిశలో విద్యుత్ ప్రవహిస్తుంది. మరియు తర్వాత అర్థ భ్రమణానికి బ్రష్ B₂ ద్వారా వ్యతిరేక దిశలో విద్యుత్ ప్రవహిస్తుంది. ఈ ప్రక్రియ కొనసాగుతూ ఏకాంతరంగా విద్యుచ్ఛాలక బలం జనిస్తుంది.

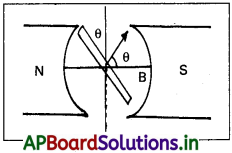
సిద్ధాంతం:
i) తీగచుట్ట స్థిర కోణీయ వేగం ω తో తిరుగుచున్నది.
ii) తీగచుట్ట యొక్క లంబానికి, అయస్కాంత క్షేత్రానికి \(\overrightarrow{B}\) ఏదైనా సమయంలో
కోణము θ = ωt ………… (1)
iii) తీగచుట్ట తలానికి లంబంగా ఉన్న అయస్కాంత క్షేత్ర అంశము B cos θ = B cosωt ………… (2)
iv) ఒక చుట్టు గల తీగచుట్టలో అయస్కాంత అభివాహం = (B cos ωt) A ………… (3)
A అనునది తీగచుట్ట వైశాల్యం మరియు n అనునది చుట్ల సంఖ్య
v) తీగచుట్టలో మొత్తం అయస్కాంత అభివాహం (Φ) = n(B cos ωt) A ………… (4)
ఫారడే నియమం ప్రకారం

విద్యుత్ ప్రవాహ దిశ ఆవర్తనంగా మారుతుంది మరియు దీనిని ఏకాంతర ప్రవాహం (A.C) అంటారు.

అభ్యాసాలు Textual Exercises

ప్రశ్న 1.
(a) నుంచి (f) వరకు గల కింద ఇచ్చిన పటాలలో వర్ణించిన పరిస్థితులలో ప్రేరిత విద్యుత్ ప్రవాహ దిశను ప్రాగుక్తీకరించండి.


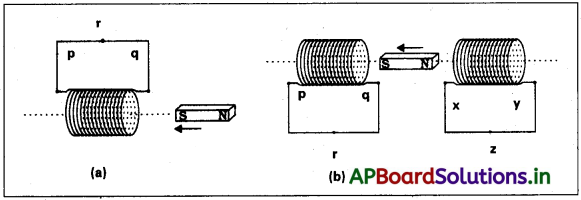
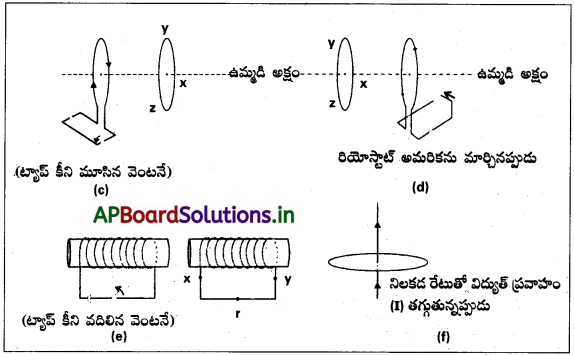
జవాబు:
a) ఇక్కడ దక్షిణ ధృవంను తీగచుట్ట వైపు కదిల్చితే లెంజ్ నియమం ప్రకారం విద్యుత్ ప్రవాహము సవ్య దిశలో ప్రవహిస్తుంది. అనగా విద్యుత్ p నుండి q కు ప్రవహిస్తుంది.

b) p-q తీగ చుట్టలో q వద్ద s ను q వైపు జరిపితే ఇది దక్షిణ ధృవం వలే పనిచేస్తుంది. విద్యుత్ ప్రవాహము సవ్య దిశలో ఉంటుంది. (అనగా p నుండి q) ఉత్తర ధృవంను దూరం జరిపితే చివర దక్షిణ ధృవం వలె పనిచేస్తుంది. విద్యుత్ ప్రవాహము సవ్య దిశలో X నుండి y కు ఉంటుంది.

c) ట్యాప్ కీని మూస్తే, తీగచుట్టలో విద్యుత్ పెరిగి, అయస్కాంత అభివాహం పెరుగుతుంది. మాక్స్వెల్ నియమం ప్రకారం‘అయస్కాంత క్షేత్రం ఎడమవైపుకు పనిచేస్తుంది. ప్రేరిత విద్యుత్ ప్రవాహ దిశ, క్షేత్రాన్ని తగ్గిస్తుంది. క్షేత్ర దిశ కుడి వైపు పనిచేస్తుంది. మాక్స్వెల్ నియమం ప్రకారం ప్రేరిత విద్యుత్ ప్రవాహ దిశ అపసవ్య దిశలో అనగా xyz దిశలో ఉండును.

d) రియోస్టాట్ను మారిస్తే, విద్యుత్ మారుతుంది. క్షేత్రదిశ ఎడమవైపు చూపుతుంది. ఎడమ తీగచుట్టలో ప్రేరిత విద్యుత్ ప్రవాహ దిశ వలన జనించే క్షేత్ర దిశ కుడివైపుకు ఉంటుంది. అందువలన ఎడమ చుట్టలో విద్యుత్ దిశ అపసవ్య దిశ అనగా Zyx దిశలో ఉండును.

e) కీని వదిలితే విద్యుత్ అపసవ్య దిశలో ప్రవహించి తగ్గుతుంది. దాని వలన ప్రేరిత విద్యుత్ జనించి, ఎడమచుట్టలో క్షేత్రం పెరుగుతుంది. కావున కుడివైపు చుట్టలో అయస్కాంత క్షేత్రం కుడివైపు పనిచేస్తుంది. కావున ప్రేరిత విద్యుత్ అపసవ్య దిశలో అనగా x నుండి yx దిశలో ఉండును.

f) విద్యుత్ ప్రవాహ తీగలో అయస్కాంత క్షేత్ర రేఖలు చుట్ట తలంలో ఉంటాయి. కావున తీగచుట్టలో ప్రేరిత విద్యుత్ జనించదు.

ప్రశ్న 2.
పటం చూపిన సందర్భాలలో ప్రేరిత విద్యుత్ ప్రవాహ దిశను నిర్ధారించడానికి లెంజ్ నియమాన్ని ఉపయోగించండి.

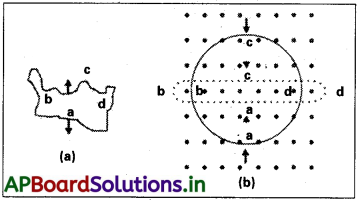
(a) అక్రమాకారంలో ఉన్న తీగ వృత్తాకారంలోకి మారుతున్నప్పుడు.
(b) వృత్తాకార లూప్ సన్నని నిలువైన తీగగా
(a) విరూపణం చెందుతున్నప్పుడు.
జవాబు:
a) ఇక్కడ అయస్కాంత క్షేత్ర దిశ కాగితపు తలానికి లంబంగా లోనికి పనిచేస్తుంది. తీగను వృత్తాకారంగా చుడితే దాని వైశాల్యం పెరుగుతుంది. అందువలన అయస్కాంత అభివాహం పెరుగుతుంది. ఆ దిశలో ప్రేరిత విద్యుత్ జనించి అయస్కాంత క్షేత్రాన్ని తగ్గిస్తుంది. విద్యుత్ ప్రవాహము అపసవ్య దిశలో అనగా adcb a దిశలో ఉండును.

b) వృత్తాకార తీగచుట్టను సన్నని తీగలాగా మార్చితే, దాని అయస్కాంత అభివాహం తగ్గుతుంది. ప్రేరిత విద్యుత్ అపసవ్య దిశలో ప్రవహిస్తుంది. అనగా a’d’c’b’a’. దీనివలన కాగితపు తలానికి వెలుపల అయస్కాంత క్షేత్రం జనిస్తుంది.

ప్రశ్న 3.
సెంటీమీటర్కు 15 చుట్లు గల పొడవైన సాలినాయిడ్ లోపల దాని అక్షానికి లంబంగా 2.0 cm3 వైశాల్యం గల చిన్న లూప్ను ఉంచారు. సాలినాయిడ్లో ప్రవహిస్తున్న విద్యుత్ ప్రవాహం 4.0 A నుంచి 2.0 A లకు 0.1 సెకనులో నిలకడగా మార్పు చెందితే, విద్యుత్ ప్రవాహం మారుతున్నప్పుడు లూప్ లో ప్రేరితమయ్యే విద్యుచ్ఛాలక బలం ఎంత?
సాధన:
చుట్ల సంఖ్య (n) = 15/cm = 1500/m
వైశాల్యం (A) = 2 cm² = 2 × 10^-4 m².

ప్రశ్న 4.
చిన్న గాటు (small cut) కలిగి, భుజాలు 8 cm, 2 cm గల ఒక దీర్ఘచతురస్రాకార లూప్ 0.3 T పరిమాణం గల ఏకరీతి అయస్కాంత క్షేత్ర ప్రాంతం నుంచి బయటకు చలిస్తుంది. క్షేత్ర దిశ లూప్కు లంబంగా ఉన్నది. లూప్ 1 cms^-1 వేగంతో (a) పెద్ద భుజానికి, (b) చిన్న భుజానికి, లంబ దిశలో కదిలితే గాటు వద్ద వృద్ధిచెందే విద్యుచ్ఛాలక బలం ఎంత? ప్రతి సందర్భంలో ప్రేరిత వోల్టేజి ఎంత సమయం పాటు ఉంటుంది?
సాధన:
తీగచుట్ట పొడవు (l) = 8 cm = 8 × 10^-2 m.
మందము (b) = 2 cm = 2 × 10^-2 m.
వేగము = 1 cm/s = 0.01 m/s
అయస్కాంత ప్రేరణ B = 0.3 T

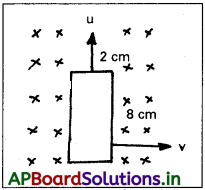
a) వేగము పొడవుగా ఉన్న వైపుకు లంబంగా ఉంటే
l = 8 cm = 8 × 10^-2 m
చలనాత్మక వి.చా.బ (e) = Blυ = 0.3 × 8 × 10^-2 × 0.01

ప్రశ్న 5.
1.0 m పొడవైన లోహ కడ్డీని కడ్డీకి లంబంగా, , కడ్డీ ఒక కొన ద్వారా పోయే అక్షం దృష్ట్యా 400 rad s^-1 కోణీయ పౌనః పున్యంతో భ్రమణం చేశారు. కడ్డీ రెండో కొన ఒక వృత్తాకార లోహ కంకణంతో స్పర్శలో కలదు. స్థిర, ఏకరీతి 0.5 T అయస్కాంత క్షేత్రం అక్షానికి సమాంతరంగా అంతటా వ్యాపించి ఉంది. కంకణం, దాని కేంద్రం మధ్య వృద్ధి చెందే విద్యుచ్ఛాలక బలాన్ని లెక్కించండి.
సాధన:

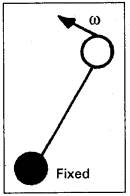
కడ్డీ యొక్క పొడవు (l) = 1m
కోణీయ పౌనఃపున్యము (ω) = 400 rad/s
అయస్కాంత ప్రేరణ (B) = 0.5 T
రేఖీయ వేగం = 0
మరొక రేఖీయ వేగం = lω

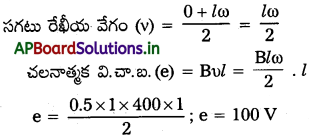
ప్రశ్న 6.
3.0 × 10^-2 T పరిమాణం గల ఏకరీతి క్షితిజ సమాంతర అయస్కాంత క్షేత్రంలో 8.0 cm వ్యాసార్థం 20 చుట్లు గల వృత్తాకార తీగచుట్టను దాని నిట్టనిలువు వ్యాసం దృష్ట్యా 50 rad s^-1 కోణీయ వడితో భ్రమణం చేశారు. తీగచుట్టలో ప్రేరితమయ్యే గరిష్ఠ, సగటు విద్యుచ్ఛాలక బలాన్ని పొందండి. తీగచుట్ట 10౧ నిరోధం గల సంవృత వలయాన్ని ఏర్పరిస్తే, తీగచుట్టలోని గరిష్ఠ విద్యుత్ ప్రవాహ విలువను లెక్కించండి. జౌల్ ఉష్టీకరణం కారణంగా జరిగే సగటు సామర్థ్య నష్టాన్ని లెక్కించండి. ఈ సామర్థ్యం ఎక్కడి నుండి వచ్చింది?
సాధన:
తీగచుట్ట వ్యాసార్థము = 8 cm = 0.08 cm
చుట్ల సంఖ్య = 20; నిరోధము = 10Ω
కోణీయ వేగము (ω) = 50 rad/s
అయస్కాంత ప్రేరణ (B) = 3 × 10^-2 T
ప్రేరిత వి.చా.బ. (e) = NBA ω sin ωt
గరిష్ఠ వి. చా. బ. sin ωt = 1

సామర్ధ్య నష్టం తీగచుట్టలో ఉష్ణం రూపంలో వెలువడును.

ప్రశ్న 7.
భూ అయస్కాంత క్షేత్ర క్షితిజ సమాంతర అంశం 0.30 × 10^-4 Wb m^-2 కి లంబంగా తూర్పు నుంచి పశ్చిమంగా విస్తరించి ఉన్న 10 m పొడవైన క్షితిజ సమాంతర తిన్నని తీగ 5.0 m s^-1 వేగంతో పడుతుంది.
(a) తీగలో ప్రేరితమైన విద్యుచ్ఛాలక బలం తాక్షణిక విలువ ఎంత?
(b) విద్యుచ్ఛాలక బలం దిశ ఏమిటి ?.
(c) తీగ ఏ కొన అధిక విద్యుత్ పొటెన్షియల్ వద్ద ఉంటుంది?
సాధన:

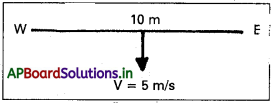
తిన్నని తీగ వేగం = 5 m/s
అయస్కాంత ప్రేరణ (B) = 0.30 × 10^-4Wb/m^-2
తీగ పొడవు l = 10m
a) తీగలో వి.చా.బ. (e) = Blυsin θ
ఇక్కడ θ = 90°, sin θ = 1
e = 0.3 × 10^-4 × 10 × 5 = 1.5 × 10^-3 V.

b) ఫ్లెమింగ్ ఎడమచేతి నియమం ప్రకారం, బలం క్రింద వైపుకు, ప్రేరిత వి. చా.బ పడమర నుండి తూర్పు వైపుకు ఉంటుంది.

c) ప్రేరిత వి.చా.బ (లేదా) విద్యుత్ దిశ పడమర నుండి తూర్పుకు ఉంటే పడమర వైపు అధిక పొటెన్షియల్ వద్ద ఉంటుంది.

ప్రశ్న 8.
ఒక వలయంలో విద్యుత్ ప్రవాహం 5.0 A నుంచి 0.0 A కి 0.1 s లో పడిపోయింది. 200 V సగటు విద్యుచ్ఛాలకు బలం ప్రేరితం అయితే, ఆ వలయం స్వయం ప్రేరకత్వాన్ని అంచనా వేయండి. [TS. Mar.’16; Mar.’14]
సాధన:
విద్యుత్ ప్రవాహంలో మార్పు (dI) = 5 – 0 = 5A
కాలంలో మార్పు (dt) = 0.1 sec

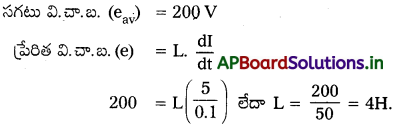
ప్రశ్న 9.
పక్కపక్కన ఉన్న ఒక జత తీగచుట్ల అన్యోన్య ప్రేరకత్వం 1.5 H. ఒక చుట్టలో విద్యుత్ ప్రవాహం 0 నుంచి 20 A లకు 0.5 s లలో మారినట్లయితే, రెండవ తీగచుట్టలో అభివాహ బంధనంలో వచ్చే మార్పు ఎంత?
సాధన:
అన్యోన్య ప్రేరణ (M) = 1.5 H
విద్యుత్ ప్రవాహంలో మార్పు (dl) 20 – 0 = 20 A
కాలంలో మార్పు (dt) = 0.5 sec
ప్రేరిత వి.చా.బ. (e) = M\(\frac{dI}{dt}=\frac{-\mathrm{d} \phi}{\mathrm{dt}}\)
dΦ = M.dI = 1.5 × 20
అభివాహంలో మార్పు (dΦ) = 30 Wb

ప్రశ్న 10.
ఒక జెట్ విమానం 1800 km/h వడితో పశ్చిమ దిశ వైపు ప్రయాణిస్తోంది. ఆ ప్రదేశపు భూఅయస్కాంత క్షేత్ర పరిమాణం 5 × 10^-4 T, అవపాత కోణం 30° అయితే 25 m వరకు వ్యాపించి ఉన్న రెక్క కొనల మధ్య వృద్ధి చెందే వోల్టేజి భేదం ఎంత?
సాధన:
జెట్ విమాన గం (V) = 1800 km/h = 1800 × \(\frac{5}{8}\) = 500 m/s
రెక్కల మధ్య దూరం (l) = 25m
అయస్కాంత ప్రేరణ (B) = 5 × 10^-4T
డిప్ కోణం (δ) = 30°
చలన వి.చా.బ. (e) = B_vVl
e = B sin δ Vl (∵ B_v = B sin δ),
e = 5 × 10^-4 + sin 30° × 500 × 25
e = 3.1 V.

అదనపు అభ్యాసాలు Additional Exercises

ప్రశ్న 11.
అభ్యాసం 4 లోని లూప్ స్థిరంగా ఉందనుకోండి. అయస్కాంత క్షేత్రాన్ని ఉత్పత్తి చేస్తున్న విద్యుదయస్కాంతానికి అందించే విద్యుత్ ప్రవాహాన్ని క్రమంగా తగ్గించడం ద్వారా క్షేత్రం తొలి విలువ 0.3 T నుంచి 0.02 T s^-1 రేటు వరకు క్షీణింపచేశారు. లూప్ ని గాటును (cut) కలిపినట్లయితే మరియు లూప్ నిరోధం 1.6Ω అయితే, లూప్ వల్ల ఎంత శక్తి ఉష్ణ రూపంలో దుర్వ్యయమవుతుంది? ఈ సామర్థ్యానికి జనకం ఏమిటి?
సాధన:
వైశాల్యం = 8 × 2 = 16 cm² 16 × 10^-4 m²

ప్రశ్న 12.
X, Y అక్షాలకు సమాంతరంగా 12 cm భుజం గల చతురస్రాకార లూప్ 8 cm s^-1 వేగంతో ధన X అక్షం దిశలో, అయస్కాంత క్షేత్రం ధన Z- అక్షం దిశ ఉన్న పరిసరం (environment) లో చలిస్తుంది. క్షేత్రం ప్రాదేశికంగా ఏకరీతిగా, కాలంతో స్థిరంగా లేదు. రుణ X- దిశలో క్షేత్రం 10^-3 T cm^-1 ప్రవణతను కలిగి ఉంది. (అంటే ధన X- దిశలో చలిస్తున్నప్పుడు క్షేత్ర విలువ 10^-3 T cm^-1” చొప్పున పెరుగుతుంది). కాలంతోపాటు 10^-3 Ts^-1 చొప్పున క్షేత్ర విలువ తగ్గుతుంది. లూప్ నిరోధం 4.50 ml అయితే, ప్రేరిత విద్యుత్ ప్రవాహం దిశను, పరిమాణాన్ని నిర్ణయించండి.
సాధన:
తీగచుట్ట భుజం (a) = 12 cm
వైశాల్యం (A) = a² = (12)² = 144 cm² = 144 × 10^-4 m²
వేగము (v) = 8 cm/s = 8 × 10^-2 m/s.
దూరంతో పాటు అయస్కాంత ప్రేరణలో మార్పు = \(\frac{dB}{dx}\) = 10^-3 T/cm

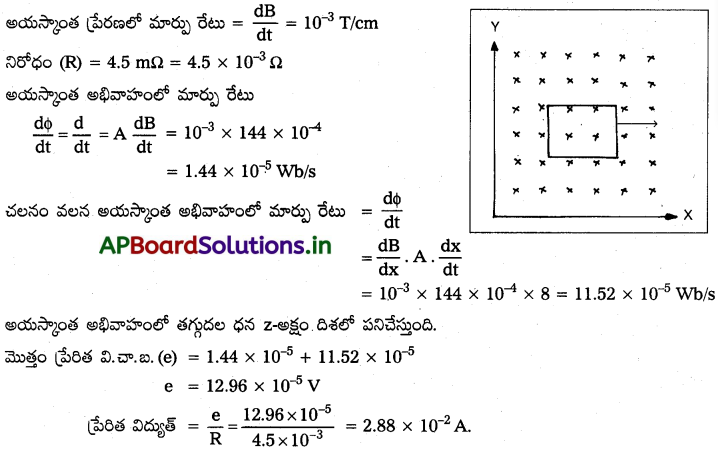
ప్రేరిత విద్యుత్ దిశ కూడా ధన Z- అక్షం దిశలోనే ఉంటుంది.

ప్రశ్న 13.
ఒక శక్తివంతమైన లౌడ్ స్పీకర్ అయస్కాంతపు ధృవాల మధ్య క్షేత్రాన్ని కొలవాలనుకున్నారు. 2 cm² వైశాల్యంతో 25 దగ్గర చుట్లు గల చిన్న సమతల శోధన తీగచుట్టను క్షేత్రానికి లంబదిశలో ఉంచి క్షేత్రం ప్రాంతం నుంచి శీఘ్రంగా బయటకు లాగారు (తుల్యంగా, ఆ తీగచుట్టను క్షేత్ర దిశకు సమాంతరంగా తీసుకొనిరావడానికి దానికి శీఘ్రంగా 90° భ్రమణం కూడా ఇవ్వచ్చు). తీగచుట్ట ద్వారా ప్రయాణించిన మొత్తం ఆవేశం (తీగకు కలిపి ప్రక్షేపక గాల్వనా మాపకం ద్వారా కొలవగా) 7.5 mC. తీగ, గాల్వనా మాపకం రెండింటి సంయోగ నిరోధం 0.50Ω అయస్కాంత క్షేత్ర సత్వాన్ని అంచనా వేయండి.
సాధన:
తీగచుట్ట వైశాల్యం (A) = 2cm² = 2 × 10^-4 m²
చుట్ల సంఖ్య (N) = 25
తీగచుట్టలో మొత్తం ఆవేశం (Q) = 7.5 mc = 7.5 × 10^-3 c
నిరోధము (R) = 0.5Ω

ప్రశ్న 14.
శాశ్వత అయస్కాంత ధృవాల మధ్య ఉంచిన నునుపైన AB పట్టాల పై PQ లోహ కడ్డీ పటంలో చూపిన విధంగా నిశ్చలంగా ఉంది. పట్టాలు, కడ్డీ, అయస్కాంత క్షేత్రం ఒకదానితో ఒకటి పరస్పరం లంబ దిశలలో ఉన్నాయి. గాల్వనీ మాపకం G స్విచ్ K ద్వారా పట్టాలను కలుపుతుంది. కడ్డీ పొడవు= 15 cm, B = 0.50 T, కడ్డీని కలిగి ఉన్న సంస్కృత లూప్ నిరోధం = 9.0 mΩ. అయస్కాంత క్షేత్రం ఏకరీతిగా ఉందనుకోండి.

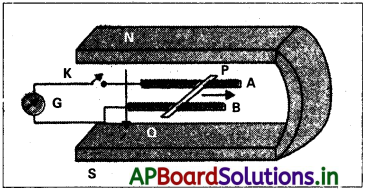
a) పటంలో చూపిన దిశలో స్విచ్ Kని తెరిచినప్పుడు కడ్డీ 12 cm s^-1 వడితో కదిలిందనుకోండి. ప్రేరిత విద్యుచ్ఛాక బలం ధృవణత, పరిమాణాన్ని ఇవ్వండి.
b) K ని తెరిచినప్పుడు కడ్డీ కొనల వద్ద ఏదైనా అదనపు ఆవేశం వృద్ధి అవుతుందా? K ని మూసినప్పుడు ఏమి జరుగుతుంది?
c) Kని తెరిచినప్పుడు, కడ్డీ ఏకరీతిగా చలిస్తున్నప్పుడు, కడ్డీ PQ లోని ఎలక్ట్రాన్లు కడ్డీ చలనం వల్ల అయస్కాంతీయ బలాన్ని అనుభవించినప్పటికీ వాటిపై పనిచేసే నికర బలం ఏమి ఉండదు. వివరించండి.
d) Kని మూసినప్పుడు, కడ్డీపై ఉండే మందక (retarding) బలం ఏమిటి?
e) Kని మూసినప్పుడు, కడ్డీని అదే వడితో (=12 cm s^-1) చలింపచేయడానికి (బాహ్య ఏజెంట్ వల్ల) ఎంత సామర్థ్యం అవసరం?
f) మూసిన (సంవృత) వలయంలో ఎంత సామర్థ్యం ఉష్ణంగా దుర్వ్యయం అయ్యింది? ఈ సామర్థ్యానికి జనకం ఏమిటి?
g) లంబ దిశకు బదులు అయస్కాంత క్షేత్ర దిశ పట్టాలకు సమాంతరంగా ఉంటే చలిస్తున్న కడ్డీలో ప్రేరితమయ్యే విద్యుచ్ఛాలక బలం ఎంత?
సాధన:
కడ్డీ పొడవు (I) = 15 cm = 15 × 10^-2 m
అయస్కాంత ప్రేరణ (B) = 0.5 T
నిరోధము (R) = 9mΩ = 9 × 10^-3Ω
కడ్డీ వేగము (V) = 12 cm/s = 12 × 10^-2 m/s.
a) చలన వి.చా.బ. () = BVI = 0.5 × 12 × 10^-2 × 15 × 10^-2
e = 9 × 10^-3 V.

ఫ్లెమింగ్ ఎడమచేతి నియమం ప్రకారం లోరెంజ్ బలం
F = – e(V × B) ఎలక్ట్రాన్లపై PQ లో P నుండి Q కు ఉంటుంది. కావున P ధనావేశమును, Q ఋణావేశమును పొందును.

b) అవును. P వద్ద అదనపు ధనావేశము ఏర్పడును. కీని తెరచినప్పుడు అంటే పరిమాణంలో Q వద్ద ఋణావేశము ఏర్పడును. కీని మూస్తే ప్రేరిత విద్యుత్ ప్రవహించి, అదనపు ఆవేశము కలిగి ఉండును.

c) కీని తెరిస్తే, ఎలక్ట్రాన్లపై ఎలాంటి బలం పనిచేయదు. అందుకు కారణం P మరియు Q వద్ద విద్యుత్ క్షేత్రం వల్ల అదనపు ఆవేశం ఏర్పడును. అయస్కాంత క్షేత్రబలం, విద్యుత్ క్షేత్ర బలానికి సమానం కావున కడ్డీపై ఫలితం శూన్యం.

d) కీని మూసివేస్తే, విద్యుత్ ప్రవహించి, విద్యుత్ ప్రవహించే తీగలో అయస్కాంత క్షేత్రం వల్ల ఋణబలం పనిచేస్తుంది.

e) కడ్డీ అదే వేగంతో ఉండుటకు అవసరమైన సామర్థ్యం = ఋణబలం × వేగం = 7.5 × 10^-2 × 12 × 10^-2 × 10^-3 W

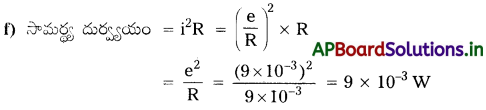
g) క్షేత్రము కడ్డీలకు సమాంతరంగా ఉంటే (8 = 0), ప్రేరిత వి.చా.బ. = e = BVl sin θ
(∵ sin θ° = (0). ఈ సందర్భంలో చలించే కడ్డీ క్షేత్ర రేఖలను ఖండించదు. కావున అభివాహంలో మార్పు శూన్యం మరియు ప్రేరిత వి.చా. బ శూన్యం.

ప్రశ్న 15.
30 cm పొడవు, 25 cm2 మధ్యచ్ఛేద వైశాల్యం, 500 చుట్లు కలిగి, గాలి కాండం (కోర్) గల సాలినాయిడ్లో 2.5 A విద్యుత్ ప్రవహిస్తోంది. విద్యుచ్ఛాలక బలం జనకం నుంచి సాలినాయిడ్ను విడదీసినప్పుడు దానిలో విద్యుత్ ప్రవాహం 10×sలో శూన్యానికి పడిపోతుంది. వలయంలో తెరిచి ఉంచిన స్విచ్ కొనల మధ్య ఏర్పడే సగటు తిరోదిశా విద్యుచ్ఛాలక బలం ఎంత ? సాలినాయిడ్ కొనల దగ్గర అయస్కాంత క్షేత్ర మార్పును ఉపేక్షించండి.
సాధన:
సాలినాయిడ్ పొడవు (1) = 30 cm = 30 × 10^-2 m
అడ్డుకోత వైశాల్యం (A) = 25 cm² = 25 × 10^-4 m²
చుట్ల సంఖ్య (N) = 500
విద్యుత్ ప్రవాహం (I₁) = 2.5A, I₂ = 0
కాలం (dt) = 10^-3 sec

ప్రశ్న 16.
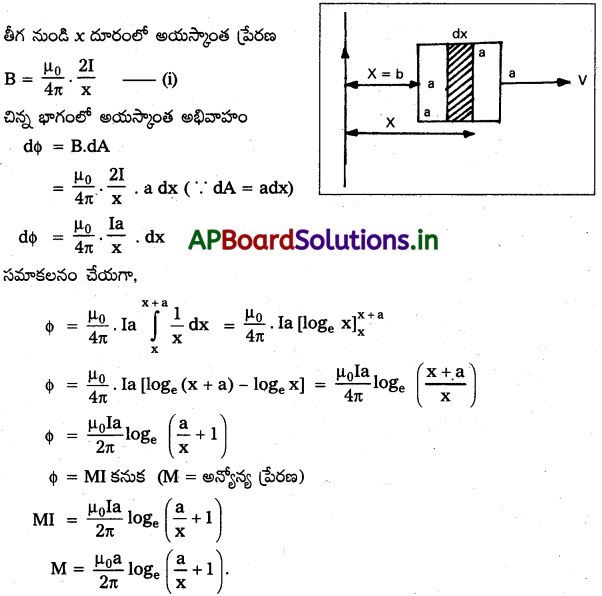
(a) పటంలో చూపిన పొడవైన తిన్నని తీగ a భుజం గల చతురస్రాకార లూప్ మధ్య ఉండే అన్యోన్య ప్రేరకత్వానికి ఒక సమాసాన్ని పొందండి.

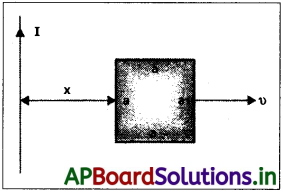
(b) ఇప్పుడు తిన్నని తీగలో 50 A విద్యుత్ ప్రవాహం ప్రవహిస్తున్నట్లు, కుడి పక్కకు, స్థిర వేగం υ = 10 m/s తో లూప్ చలించినట్లు భావించండి. x = 02mఅయిన సందర్భంలో లూప్లో ప్రేరితమయ్యే విద్యుచ్ఛాలక బలాన్ని లెక్కించండి. a = 0.1 m గా తీసుకొని, లూప్ చాలా అధిక నిరోధాన్ని కలిగి ఉన్నట్లుగా భావించండి.
సాధన:
a) ఒక అల్పాంశము మందము dx. ఇది తీగనుండి దూరంలో ఉంది. తీగలో విద్యుత్ ప్రవాహము I.
చతుర్భుజము పొడవు = a

ప్రశ్న 17.
M ద్రవ్యరాశి, R వ్యాసార్థం గల చక్రం అంచుకు ఏకరీతిగా ఏకాంక పొడవుకు రేఖీయ ఆవేశం)ఇవ్వడమైంది. చక్రం తేలికైన అవాహక ఊచ (ఆకు—spoke) లు కలిగి, ఘర్షణ లేకుండా స్వేచ్ఛగా దాని అక్షం దృష్ట్యా భ్రమణం చేయగలదు. ఏకరీతి అయస్కాంత క్షేత్రం చక్రం అంచులోపల వృత్తాకార ప్రాంతం అంతా విస్తరించి ఉంది. దీనిని

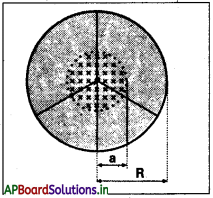
B=-B₀k (r ≤ a; a < R)
= 0 (మరొక విధంగా otherwise)
గా సూచించారు. క్షేత్రాన్ని ఒక్కసారిగా ఆపివేసిన (switched off) తరువాత చక్రం కోణీయ వేగం ఎంత ?
సాధన:

సాధించిన సమస్యలు Textual Examples

ప్రశ్న 1.
a) గాల్వనామీటర్లో అధిక అపవర్తనం పొందడానికి మీరు ఏం చేస్తారు? (b) గాల్వనా మీటర్ లేకుండా వలయంలో ప్రేరిత విద్యుత్ ప్రవాహం ఉండటాన్ని ప్రాయోగికంగా ఏ విధంగా ప్రదర్శిస్తారు?
సాధన:
a) గాల్వనామీటర్లో అధిక అపవర్తనాన్ని పొందడానికి కింది విధంగా ఒకటి లేదా అంతకంటే ఎక్కువ విధానాలను అవలంబించవచ్చు. (i) తీగచుట్ట C, లోపల మెత్తని ఇనుపకడ్డీని ఉపయోగించడం, (ii) తీగచుట్టను శక్తివంతమైన బ్యాటరీకి అనుసంధానం చేయడం, (iii) అమరికనంతా తీగచుట్ట C, వైపు వేగంగా జరపడం.

b) వలయంలో గాల్వనామీటర్కు బదులుగా చిన్న టార్చ్ లైట్ ఉపయోగించే చిన్న బల్బును ఉపయోగించండి. ఈ రెండు తీగచుట్టల మధ్య సాపేక్ష చలనం బల్బు, వెలిగేలా చేస్తుంది. ఈ విధంగా ప్రేరిత ప్రవాహం ఉండటాన్ని ప్రాయోగికంగా ప్రదర్శించవచ్చు.

ప్రయోగ భౌతికశాస్త్రంలో ఎవరైనా నూతన రీతుల కల్పనను నేర్చుకోవాల్సి ఉంటుంది. అత్యుత్తమ ప్రయోగవేత్తలలో ఒకరుగా, శాశ్వతంగా ఉన్నత స్థానంలో ఉన్న మైఖేల్ ఫారడే నూతన రీతులను కనుక్కొనే నైపుణ్యం వల్ల చారిత్రకంగా ప్రసిద్ధి చెందాడు.

ప్రశ్న 2.
భుజం 10 cm, నిరోధం 0.5 Ωలు గల ఒక చతురస్రాకార లూప్ను తూర్పు – పడమర తలానికి నిలువుగా ఉంచారు. దాని తలం వెంట 0.10 T తీవ్రత గల ఏకరీతి అయస్కాంత క్షేత్రాన్ని ఉత్తర – దక్షిణ దిశల్లో ఏర్పాటు చేశారు. అయస్కాంత క్షేత్రాన్ని నిలకడ రేటుతో 0.70 s లలో శూన్యానికి తగ్గించారు. ఈ కాల వ్యవధిలో ప్రేరిత విద్యుచ్ఛాలక ‘బలం, ప్రవాహాల పరిమాణాలను కనుక్కోండి.
సాధన:
తీగచుట్ట వైశాల్య సదిశ, అయస్కాంత క్షేత్ర దిశతో చేసే కోణం θ = 45°.

భూ అయస్కాంత క్షేత్రం కూడా లూప్ ద్వారా అభివాహాన్ని జనింపచేస్తుంది అని గమనించండి. కాని ఇది నిలకడ క్షేత్రం (ప్రయోగం జరుగుతున్నంత కాలం మారకుండా ఉండేది) కాబట్టి అది ఏ విధమైన విద్యుచ్ఛాలక బలాన్ని ప్రేరేపించదు.

ప్రశ్న 3.
వ్యాసార్థం 10 cm, నిరోధం 2 Ω, 500 చుట్లు ఉన్న ఒక వృత్తాకార తీగచుట్ట తలాన్ని భూఅయస్కాంత క్షేత్ర క్షితిజ సమాంతర అంశానికి లంబంగా ఉండేటట్లు ఉంచారు. ఈ. తీగచుట్టను దాని నిలువు వ్యాసం పరంగా 0.25 s కాలంలో 180° భ్రమణం చెందించారు. ఆ తీగచుట్టలో ప్రేరితమైన విద్యుచ్ఛాలక బలం, ప్రవాహాలను అంచనావేయండి. ఆ ప్రదేశంలో భూ అయస్కాంత క్షేత్ర క్షితిజ సమాంతర అంశం 3.0 × 10^-5 T.
సాధన:
తీగచుట్ట ద్వారా తొలి అభివాహం, Φ_{B(తాలి)} = BA cos θ = 3.0 × 10^-5 × (π. × 10^-2) × COS 0°
= 3π × 10^-7 Wb.

భ్రమణం చెందిన తరువాత తుది అభివాహం, Φ_{B(తుది)} = 3.0 × 10^-5 × (π × 10^-2) × cos 180°
= -3π × 10^-7 Wb.

కాబట్టి, ప్రేరిత విద్యుచ్ఛాలక బలం యొక్క అంచనా విలువ,
ε = N\(\frac{\Delta \phi}{\Delta \mathrm{t}}\) = 500 × (6π × 10^-7)/0.25 = 3.8× 10^-3 v
I = ε/R = 1.9 × 10^-3 A.

ε, I ల పరిమాణాలు అంచనావేసిన విలువలు అని గమనించండి. వాటి తక్షణ విలువలు వేరుగా ఉండి, అవి ఆ క్షణం వద్ద తీగచుట్ట భ్రమణ వడిపై ఆధారపడతాయి.

ప్రశ్న 4.
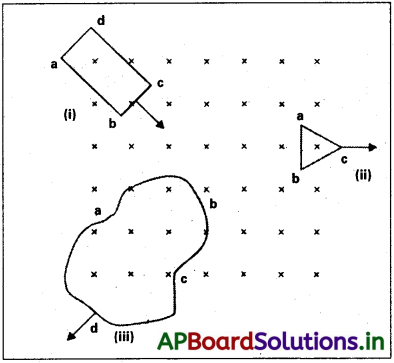
పటంలో చూపినట్లు వివిధ ఆకృతులు గల సమతల లూప్లు వాటి తలాలకు లంబంగా (పాఠకుని నుంచి దూరంగా) ఉన్న అయస్కాంత క్షేత్రం (పుటతలం నుంచి లోపలికి ఉన్న) లోకి, బయటకు చలిస్తున్నాయి. లెంజ్ నియమం ప్రకారం ప్రతి లూప్ ని ప్రేరిత విద్యుత్ ప్రవాహ దిశను నిర్ణయించండి.

సాధన:
i) దీర్ఘ చతురస్రాకార లూప్ abcd అయస్కాంత క్షేత్రంలోకి చలించడం వల్ల దాని ద్వారా అయస్కాంత అభివాహం పెరుగుతుంది. ప్రేరిత విద్యుత్ ప్రవాహం తప్పకుండా పథం వెంబడి ప్రవహించాలి. అప్పుడే అది పెరిగే అభివాహాన్ని వ్యతిరేకిస్తుంది.
ii) త్రిభుజాకార ఉచ్చు abc అయస్కాంత క్షేత్రం నుంచి బయటకు చలించడం వల్ల దాని ద్వారా పోయే అయస్కాంత అభివాహం తగ్గుతుంది. దీనివల్ల ప్రేరిత విద్యుత్ ప్రవాహం అభివాహంలోని మార్పును వ్యతిరేకించేలా bacd వెంబడి ప్రవహిస్తుంది.
iii) అక్రమాకార ఉచ్చు abcd అయస్కాంత క్షేత్ర ప్రాంతం నుంచి బయటకు చలించడం వల్ల దాని ద్వారా అయస్కాంత అభివాహం తగ్గడం వల్ల, అభివాహంలోని మార్పును వ్యతిరేకించేలా ప్రేరిత విద్యుత్ ప్రవాహం cdabc వెంబడి ప్రవహిస్తుంది.

అయితే లూప్లు పూర్తిగా అయస్కాంత క్షేత్రం లోపల గాని, బయటగాని ఉన్నంత వరకు ఎలాంటి ప్రేరిత విద్యుత్ ప్రవాహం ఉండదని గమనించండి.

ప్రశ్న 5.
a) స్థిరంగా బిగించి ఉన్న రెండు శాశ్వత అయస్కాంతాల ఉత్తర దక్షిణ ధృవాల మధ్య అయస్కాంత క్షేత్రంలో ఒక సంవృత లూపు స్థిరంగా ఉంచారు. చాలా బలమైన అయస్కాంతాలను ఉపయోగించి ఆ లూప్ ద్వారా విద్యుత్ ప్రవాహాన్ని ఉత్పత్తి చేసే అవకాశం కలదా?
b) ఒక పెద్ద కెపాసిటర్ పలకల మధ్య స్థిర విద్యుత్ క్షేత్రానికి లంబంగా ఒక సంవృత లూప్ చలిస్తుంది. ఆ సంవృత లూప్ (i) పలకల మధ్య ప్రదేశం లోపల పూర్తిగా మధ్యలో ఉన్నప్పుడు, (ii) పలకల నుంచి పాక్షికంగా బయటకు ఉన్నప్పుడు దానిలో విద్యుత్ ప్రవాహం ప్రేరితమవుతుందా? విద్యుత్ క్షేత్రం లూప్ తలానికి లంబంగా ఉన్నది.
c) పటంలో మాదిరిగా, ఒక దీర్ఘచతురస్రాకార లూప్, వృత్తాకార లూప్లు ఏకరీతి అయస్కాంత క్షేత్రం నుంచి బయటవైపుకు క్షేత్రరహిత ప్రాంతానికి V స్థిర వేగంతో చలిస్తున్నాయి. ఆ లూప్ల తలాలకు అయస్కాంత క్షేత్రం లంబంగా ఉన్నది. ప్రేరిత విద్యుచ్ఛాలక బలం స్థిరంగా ఉంటుందని మీరు అయితే క్షేత్రం నుంచి బయటకి పోతున్నప్పుడు ఏ లూప్లో ఆశించగలరు?

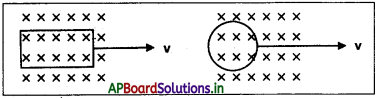
d) పటం ద్వారా వర్ణించిన పరిస్థితిలో కెపాసిటర్ ధృవణతను ఊహించండి.

సాధన:
a) ఉత్పత్తి చేయలేం. అయస్కాంతం ఎంత బలమైనది అయినప్పటికీ లూప్ ద్వారా పోయే అయస్కాంత అభివాహాన్ని ‘ మార్చడం వల్ల మాత్రమే విద్యుత్ ప్రవాహాన్ని ప్రేరేపితం చేయవచ్చు.

b) ఏ సందర్భంలోను ఎలాంటి విద్యుత్ ప్రవాహం ప్రేరితం కాదు. విద్యుత్ అభివాహాన్ని మార్చడం వల్ల విద్యుత్ ప్రవాహాన్ని ప్రేరేపితం చేయలేం.

c) దీర్ఘచతురస్రాకార లూప్ విషయంలో మాత్రమే ప్రేరిత విద్యుచ్ఛాలక బలం స్థిరంగా ఉంటుందని ఆశించవచ్చు. వృత్తాకార లూప్ విషయంలో, అది క్షేత్ర ప్రాంతం నుంచి బయటకు వచ్చేటప్పుడు దాని వైశాల్యంలోని మార్పు రేటు స్థిరంగా ఉండదు. అందువల్ల దానికి అనుగుణంగా ప్రేరిత విద్యుచ్ఛాలక బలం మారుతుంది.

d) కెపాసిటర్ B పలక పరంగా, A పలక ధృవణత ధనాత్మకంగా ఉంటుంది.

ప్రశ్న 6.
1m పొడవు ఉన్న ఒక లోహపు కడ్డీని 1m వ్యాసార్థం గల వృత్తాకార లోహపు కంకణం కేంద్రం వద్ద కడ్డీ ఒక చివర, కంకణం పరిధి వద్ద మరొక చివర ఉండేటట్లుగా ఉంచి, కంకణం కేంద్రం ద్వారా పోతూ, కంకణ తలానికి లంబంగా ఉండే అక్షం పరంగా 50 rev/ S పౌనఃపున్యంతో భ్రమణం చెందించారు. 1 T ఏకరీతి, స్థిర అయస్కాంత క్షేత్రం, అక్షానికి సమాంతరంగా అంతటా ఉంది. లోహపు కంకణానికి, కేంద్రానికీ మధ్య విద్యుచ్ఛాలక బలం ఎంత?

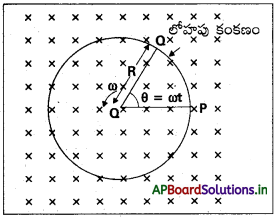
సాధన:
పద్ధతి – I :
కడ్డీ భ్రమణం చెందినప్పుడు, కడ్డీలోని స్వేచ్ఛా ఎలక్ట్రాన్లు లోరెంజ్ బలం వల్ల బయట చివరివైపు చలించి, కంకణంపై వితరణ చెందుతాయి. ఈ విధంగా వేరయిన ఆవేశాలు కడ్డీ చివరల మధ్య విద్యుచ్ఛాలక బలాన్ని ఉత్పత్తి చేస్తాయి. ఒక నిర్ణీత విద్యుచ్ఛాలక బలం విలువ వద్ద ఇక ఎలక్ట్రాన్ల ప్రవాహం ఉండక నిలకడ స్థితి చేరుతుంది. -సమీకరణం – Bl\(\frac{dx}{dt}\) = dx = Blυ ని ఉపయోగించి, కడ్డీ అయస్కాంత క్షేత్రానికి లంబంగా చలించినప్పుడు కడ్డీ పొడవు dr చివరల మధ్య ఉత్పత్తి అయిన విద్యుచ్ఛాలక బల పరిమాణం

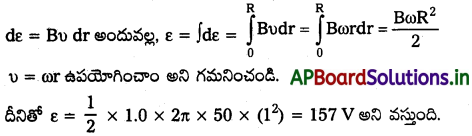
పద్ధతి – II :
విద్యుచ్ఛాలక బలాన్ని లెక్కించడానికి ఒక సంవృత లూప్ OPQ ని ఊహించవచ్చు. దీనిలో బిందువులు 0, P లు నిరోధకం Rతో సంధానం అయి ఉంటే, 0Q అనేది భ్రమణం చెందే కడ్డీ. నిరోధకం కొనల మధ్య పొటెన్షియల్ భేదం అప్పుడు ప్రేరిత విద్యుచ్ఛాలక బలానికి సమానమవుతుంది. అది B × (లూప్ వైశాల్యం మార్పురేటు) కు సమానం. θ అనేది t కాలం వద్ద కడ్డీకి, P వద్ద వృత్త వ్యాసార్థానికి మధ్య కోణం అయితే, OPQ భాగం (సెక్టార్) వైశాల్యం,

ఈ సమాసం, పద్ధతి – I ద్వారా పొందిన సమాసంతో సర్వసమంగా ఉంది. మనం ఒకే ε విలువను పొందుతాం.

ప్రశ్న 7.
ఒక్కొక్కటి 0.5 m పొడవున్న 10 లోహపు కమ్మీలు (పుల్లలు – spokes) గల ఒక చక్రాన్ని 120 rev/min వడితో ఒక ప్రదేశంలో భూఅయస్కాంత క్షేత్ర క్షితిజ సమాంతర అంశానికి లంబంగా ఉండే తలంలో భ్రమణం చెందించారు. ఆ ప్రదేశంలో H_E = 0.4 G (గ్రాస్) అయితే చక్రం ఇరుసు (అక్షం) కు, చక్రం అంచు (రిమ్)కు మధ్య ప్రేరిత విద్యుచ్ఛాలక బలం ఎంత? 1G = 10^-4 T అని గమనించండి.
సాధన:
ప్రేరిత విద్యుచ్ఛాలక బలం = (1/2) ωBR² (పై problem నుంచి)
= (1/2) × 4π × 0.4 × 10^-4 × (0.5)² = 6.28 × 10^-5 v
చక్రం కమ్మీల సంఖ్య అముఖ్యమైంది. ఎందుకంటే, కమ్మీల చివరల విద్యుచ్ఛాలక బలాలు సమాంతరం.

ప్రశ్న 8.
పటం (a) చూడండి. ఇందులో PQRS దీర్ఘ చతురస్ర వాహకంలో PQ భుజం X = 0 నుంచి బయటవైపుకు చలించింది.

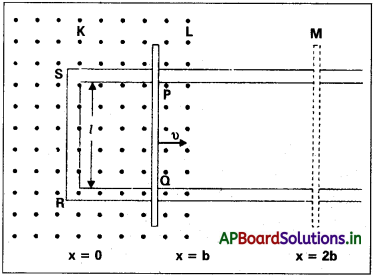
x = 0 నుంచి x = b వరకు ఏకరీతి అయస్కాంత క్షేత్రం విస్తరించి, ఆ పైన x > b కి శూన్యం అయ్యే విధంగా ఉండి, ఈ వాహక తలానికి అయస్కాంత క్షేత్రం లంబంగా ఉన్నది. PQ భుజం మాత్రమే చెప్పుకోదగిన నిరోధం rని కలిగి ఉంది. PQ భుజాన్ని x = 0 నుండి x = 2b వరకు బయటవైపుకు లాగి తిరిగి x = 0 వరకు స్థిర వడితో జరిపే పరిస్థితిని పరిగణించండి. అప్పుడు అభివాహం, ప్రేరిత విద్యుచ్ఛాలక బలం PQ భుజాన్ని లాగడానికి కావలసిన బలం, జౌల్ ఉష్ణం రూపంలో దుర్వ్యయం అయ్యే సామర్థ్యాలకు సమాసాలను పొందండి. ఈ రాశుల మార్పులను చిత్రీకరించండి.
సాధన:
ముందుగా PQ భుజం x = 0 నుంచి x = 2b వరకు ముందుకు కదిలే సందర్భాన్ని తీసుకోండి.
అప్పుడు వలయం SPQR తో బంధితమైన అభివాహం
Φ_B అనుకుంటే,
Φ_B = Blx 0 ≤ x< b
= Blb b ≤ x < 2b

ప్రేరిత విద్యుచ్ఛాలక బలం,

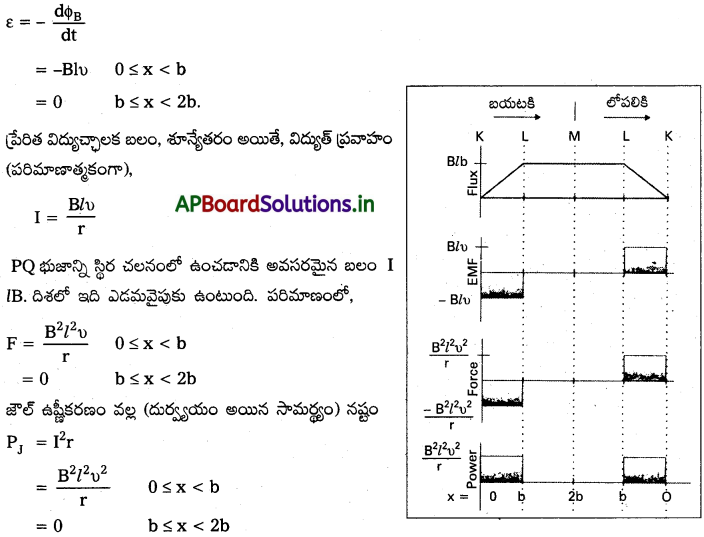
x = 2b నుంచి x = 0 కి లోపలికి చలింపచేసినప్పుడు కూడా ఇదే విధమైన సమాసాలను పొందుతారు. పటం (b) లో ప్రదర్శించిన వివిధ రాశుల రేఖాచిత్రాన్ని పరీక్షించిన తరువాత ఈ మొత్తం ప్రక్రియను ఒకరు అంచనా కట్టవచ్చు.

ప్రశ్న 9.
ఒకటి తక్కువ వ్యాసార్థం r₁, మరొకటి అధిక వ్యాసార్థం r₂, కలిగి, r₁, << r₂ అయ్యే విధంగా ఉన్న రెండు ఏక కేంద్ర వృత్తాకార తీగచుట్టలను వాటి కేంద్రాలు ఏకీభవించేలా సహాక్షంగా ఉంచారు. ఈ అమరిక అన్యోన్య ప్రేరకత్వాన్ని పొందండి.
సాధన:
బాహ్య వృత్తాకార తీగ చుట్టలో I₂, విద్యుత్ ప్రవహిస్తుందనుకోండి. అప్పుడు ఆ తీగచుట్ట కేంద్రం వద్ద అయస్కాంత క్షేత్రం B₁ = µ₀I₂/2r₂. దీనితో సహాక్షంగా ఉంచిన తీగచుట్ట చాలా తక్కువ వ్యాసార్థం కలిగి ఉన్నది. కాబట్టి దాని మధ్యచ్ఛేదంపై అయస్కాంత క్షేత్రం B₂ స్థిరంగా ఉన్నట్లు భావించవచ్చు.

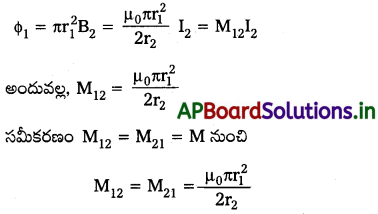
π r²₁ వైశాల్యంపై అయస్కాంత క్షేత్రం B₂ ఏకరీతిగా ఉంటుందనుకొని, Φ₁ యొక్క ఉజ్జాయింపు విలువ నుంచి M₁₂ ని లెక్కించామని గమనించండి. ఏదేమైనప్పటికీ, మనం ఈ విలువను అంగీకరించవచ్చు. ఎందుకంటే r₁ << r₂.

ప్రశ్న 10.
a) సాలినాయిడ్లో నిల్వ ఉండే అయస్కాంత శక్తికి సమాసాన్ని అయస్కాంత క్షేత్రం B, సాలినాయిడ్ వైశాల్యం A, పొడవు l పదాలలో పొందండి.
b) ఏ విధంగా ఈ అయస్కాంత శక్తి, కెపాసిటర్లో నిల్వ ఉండే స్థిర విద్యుత్ శక్తితో పోల్చదగింది?
సాధన:

రాబట్టినవి. అయితే, అవి అయస్కాంత క్షేత్రం లేదా (మరియు) విద్యుత్ క్షేత్రం ఉన్నటువంటి అంతరాళంలోని ఏ ప్రదేశంలో అయినా వర్తిస్తాయి.

ప్రశ్న 11.
నిశ్చల స్థితిలో ఉన్న సైకిల్ పెడల్స్ను కమల తొక్కుతోంది. ఈ పెడల్స్ను 0.10 m2 వైశాల్యం, 100 చుట్లు ఉన్న తీగచుట్టకు కలిపారు. ఈ తీగచుట్ట సెకనుకు అర్ధ పరిభ్రమణం చొప్పున భ్రమణం చేస్తుంది. తీగచుట్టను తీగచుట్ట భ్రమణాక్షానికి లంబంగా ఉండే 0.01 T ఏకరీతి అయస్కాంత క్షేత్రంలో ఉంచారు. తీగచుట్టలో గరిష్ఠంగా ఉత్పత్తి అయ్యే వోల్టేజి ఎంత?
సాధన:
ఇక్కడ f = 0.5 Hz; N = 100, A = 0.1 m², B = 0.01 T.
సమీకరణం ε = NBA @ sin ot ని ఉపయోగించగా.
ε₀ = NBA (2πv)
= 100 × 0.01 × 0.1 × 2 × 3.14 × 0.5 = 0.314 V
గరిష్ఠ వోల్టేజి 0.314 V