Students get through Maths 1B Important Questions Inter 1st Year Maths 1B Three Dimensional Coordinates Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B Three Dimensional Coordinates Important Questions
Question 1.
Show that the points A(-4, 9, 6), B(-1, 6, 6) and C(0, 7, 10) from a right angled isosceles triangle.
Solution:
A(-4, 9, 6), B(-1, 6, 6), C(0, 7, 10) are the vertices of ∆ABC.
AB = \(\sqrt{(-4+1)^{2}+(9-6)^{2}+(6-6)^{2}}\)
= \(\sqrt{9+9}\)
= \(\sqrt{18}\)
BC = \(\sqrt{(-1-0)^{2}+(6-7)^{2}+(6-10)^{2}}\)
= \(\sqrt{1+1+16}\) = \(\sqrt{18}\)
CA = \(\sqrt{(0+4)^{2}+(7-9)^{2}+(10-6)^{2}}\)
= \(\sqrt{16+4+16}\) = \(36\)
AB = BC and AB2 + BC2 = CA2
ABC is a right angled isosceles triangle.
![]()
Question 2.
Show that locus of the point whose distance from Y-axis is thrice its distance from (1, 2, -1) is 8x2 + 9y2 + 8z2 – 18x – 36y + 18z + 54 = 0.
Solution:
Let P (x, y, z) be any point on the locus PM – distance from Y – axis = \(\sqrt{x^{2}+z^{2}}\)
A(1, 2, -1) is the given point
Given condition is PM = 3 . PA
PM2 = 9PA2
x2 + z2 = 9[(x – 1)2 + (y – 2)2 + (z + 1)2]
= 9x2 – 18x + 9 + 9y2 – 36y + 36 + 9z2 + 18z + 9
Locus of P is 8x2 + 9y2 + 8z2 – 18x – 36y + 18z + 54 = 0
P satisfies the equation
8x2 + 9y2 + 8z2 – 18x – 36y + 18z + 54 = 0
Question 3.
A, B, C are three points on \(\overrightarrow{o x}\), \(\overrightarrow{o y}\), \(\overrightarrow{o z}\) respectively at distances a, b, e. (a ≠ 0, b ≠ 0, c ≠ 0) from the origin 0. Find the co-ordinates of the point which is equidistant from A, B, C and O.
Solution:
A is a point on ox ⇒ co-ordinates of A are (a, 0, 0)
Similarly co-ordinates of B are (0, b, 0) and co-ordinates of C are (0, 0, c)
P(x, y, z) is the required point
PO = PA = PB = PC
PO2 = PA2 = PB2 = PC2
PO2 = PA2
x2 + y2 + z2 = (x – a)2 + y2 + z2
x2 – x2 + a2 – 2ax = 0
2ax = a2 ⇒ x = \(\frac{a^{2}}{2 a}\) = \(\frac{a}{2}\)
PO2 = PB2 ⇒ y = b/2
PO2 = PC2 ⇒ z = c/2
Co-ordinates of P are (\(\frac{a}{2}\), \(\frac{b}{2}\), \(\frac{c}{2}\) )
![]()
Question 4.
Show that the points A (3, -2, 4) B(1, 1, 1) and C(-1, 4, -2) are collinear.
Solution:
A(3, -2, 4), B(1, 1, 1), C(-1, 4, -2) are the given points

A, B, C are collinear.
Question 5.
Find the ratio in which YZ-plane divides the line joining A(2, 4, 5) and B(3, 5, -4). Also find the point of intersection
Solution:
Suppose the line AB meets YZ plane in P
Let P divide AB in the ratio k : 1
Co-ordinates of P are
\(\left(\frac{3 k+2}{k+1}, \frac{5 k+4}{k+1}, \frac{-4 k+5}{k+1}\right)\)
P is a point on YZ plane
⇒ x co-ordinates of p = 0
\(\frac{3 k+2}{k+1}\) = 0 ⇒ 3k + 2 = 0
k = –\(\frac{2}{3}\)
YZ plane divides AB is the ratio -2 : 3
Substituting the value of k in co-ordinates of p, co-ordinates of p are
\(\left[0, \frac{5\left(-\frac{2}{3}\right)+4}{-\frac{2}{3}+1} \cdot \frac{(-4)\left(-\frac{2}{3}\right)+5}{-\frac{2}{3}+1}\right]\)
(0, 2, 23)
Question 6.
Show that the points A(3, -2, 4), B(1, 1, 1) and C(-1, 4, -2) are collinear.
Solution:
Suppose the point P divides AD in the ratio k : 1
Co-ordinates of P are \(\left(\frac{k+3}{k+1}, \frac{k-2}{k+1}, \frac{k+4}{k+1}\right)\)
If A, B, C are collinear, C lies on AB
P must coincide with C for same value of k
\(\frac{k+3}{k+1}\) = -1 ⇒ k + 3 = -k – 1
2k = 4 ⇒ k = -2
Substituting k = -2 in co—ordinates of P we get
\(\left(\frac{-2+3}{-2+1}, \frac{-2-2}{-2+1}, \frac{-2+4}{-2+1}\right)\)
= (-14, -2) = c
A, B, C are collinear.
![]()
Question 7.
Find the fourth vertex of the parallelogram whose consecutive vertices are (2, 4, -1), (3, 6, -1) are (4, 5, 1) [Mar 11]
Solution:
ABCD is a parallelogram
where A = (2, 4, -1), B = (3, 6, -1) C = (4, 5, 1)
Suppose D(x, y, z) is the fourth vertex
A B C D is a parallellelogram
Mid point of AC = Mid point of BD

∴ Co-ordinates of the fourth vertex are = D (3, 3, 1)
Question 8.
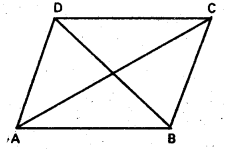
A(5, 4, 6), B(1, -1, 3), C(4, 3, 2) are three points. Find the co-ordinates of the point in which the bisector of ∠BAC meets the side \(\overline{B C}\).
Solution:
We know that if AB is the bisector of ∠BAC
Divides BC in the ratio AB : AC
![]()
Question 9.
If (x1, y1, z1) and (x2, y2, z2) are two vertices and (α, ß, γ) is the centroid of a triangle, find the third vertex of the triangle.
Solution:
Let A = (x1, y1, z1) and B = (x2, y2, z2) be the two vertices of the triangle ABC.
Let G = (α, β, γ) be the centroid.
If C = (x3, y3, z3) is the third vertex, then we have
(\(\frac{x_{1}+x_{2}+x_{3}}{3}\), \(\frac{y_{1}+y_{2}+y_{3}}{3}\), \(\frac{z_{1}+z_{2}+z_{3}}{3}\)) = (α, β, γ)
⇒ x1 + x2 + x3 = 3α; y1 + y2 + y3 = 3β; z1 + z2 + z3 = 3γ.
⇒ x3 = 3α – x1 – x2; y3 = 3β – y1 – y2; z3 = 3γ – z1 – z2.
∴ The third vertex
C = (3α – x1 – x2, 3β – y1 – y2, 3γ – z1 – z2).
Question 10.
If D(x1, y1, z1), E(x2, y2, z2) and F(x3, y3, z3) are the midpoints of the sides BC, CA and AB respectively of a triangle, find its vertices A, B and C.
Solution:
It is given that D is the mid point of the side BC, E is the mid point of the side CA and F is the mid point of the side AB.
∴ DEP is the triangle formed out of the mid points of the three sides.
Consider the parallelogram AEDF. Let A = (h, k, s).
Mid point of AD = Mid point of EF
⇒ (\(\frac{h+x_{1}}{2}\), \(\frac{k+y_{1}}{2}\), \(\frac{s+z_{1}}{2}\)) = (\(\frac{x_{2}+x_{3}}{2}\), \(\frac{y_{2}+y_{3}}{2}\), \(\frac{z_{2}+z_{3}}{2}\))
⇒ h = x2 + x3 – x1; k = y2 + y3 – y1; s = z2 + z3 – z1
∴ Vertex A
= (x2 + x3 – x1, y2 + y3 – y1, z2 + z3 – z1)
Similarly, the vertices B and C can be obtained as
B = (x3 + x1 – x2, y3 + y1 – y2, z3 + z1 – z2)
C = (x1 + x2 – x3, y1 + y2 – y3, z1 + z2 – z3).
![]()
Question 11.
If M(α, β, γ) is the mid point of the line segment joining the points A(x1, y1, z1) and B, then find B.
Solution:
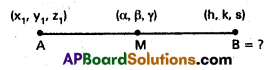
Let B(h, k, s) be the point required.
It is given that M is the mid point of AB.
∴ We have (α, β, γ) = (\(\frac{x_{1}+h}{2}\), \(\frac{y_{1}+k}{2}\), \(\frac{z_{1}+s}{2}\))
⇒ 2α = x1 + h; 2β = y1 + k; 2γ = z1 + s
⇒ h = 2α – x1; k = 2β – y1; s = 2γ – z1
∴ Point Bis (2α – x1, 2β – y1, 2γ – z1).
Question 12.
If H, G, S and I respectively denote orthocentre, centroid, circumcentre and in-centre of a triangle formed by the points (1, 2, 3), (2, 3, 1) and (3, 1, 2), then find H, G, S, I.
Solution:
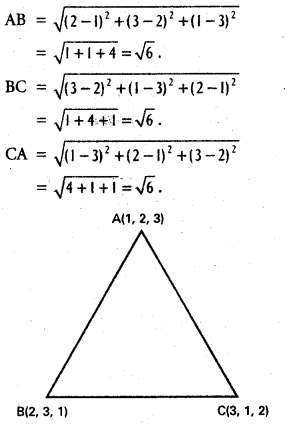
Since AB = BC = CA, ABC is equilateral triangle.
We know that orthocentre, centroid, circumcentre and incentre of equilateral triangle are the same (i.e., all the four points coincide). Now, centroid .
G = (\(\frac{1+2+3}{3}\), \(\frac{2+3+1}{3}\), \(\frac{3+1+2}{3}\))
= (2, 2 ,2)
∴ H = (2, 2, 2), S = (2, 2, 2), I = (2, 2, 2).
![]()
Question 13.
Find the incentre of the triangle formed by the points (0, 0, 0), (3, 0, 0) and (0, 4, 0).
Solution:
If a, b, care the side of the triangle ABC, where
A = (x1, y1, z1), B = (x2, y2, z2), C = (x3, y3, z3) are the vertices, then the in-centre of the triangle is given by
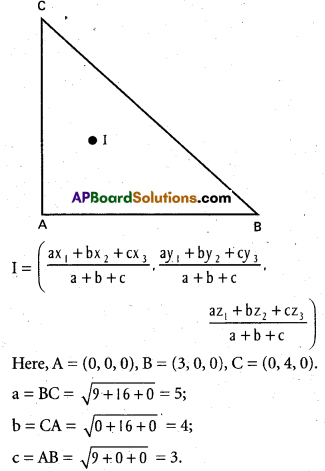
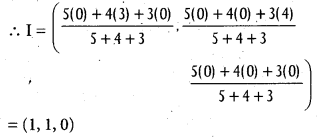
Question 14.
If the point (1, 2, 3) is changed to the point (2, 3, 1) through translation of axes, find the new origin.
Solution:
Let (x, y. z) be the co-ordinates of any point P w.r.t. the co-ordinate frame Oxyz and (X, Y, Z) be the co-ordinates of P w.r.t the new frame of reference O’XYZ.
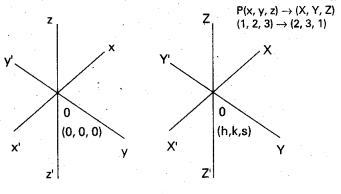
Let O’ (h, k, s) be the new origin so that
x = X + h, y = Y + k and z = Z + s.
⇒ (h, k, s) (x – X, y – Y, z – Z)
⇒ (h, k, s) = (1 – 2, 2 – 3, 3 – 1)
= (-1, -1, 2).
∴ O’ = (-1, -1, 2) is the new origin.
![]()
Question 15.
Find the ratio in which the point P(5, 4, -6) divides the line segment joining the points (3, 2, -4) and B(9, 8, -10). Also, find the harmonic conjugate of P.
Solution:

∴ Q(-3, -4, 2) is the harmonic conjugate of P(5, 4, -6).