Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(a)
I.
Question 1.
Form polynomial equations of the lowest degree, with roots as given below.
(i) 1, -1, 3
Solution:
Equation having roots α, β, γ is (x – α) (x – β) (x – γ) = 0
Sol. Required equation is (x – 1) (x + 1) (x – 3) = 0
⇒ (x2 – 1) (x – 3) = 0
⇒ x3 – 3x2 – x + 3 = 0
(ii) 1 ± 2i, 4, 2
Solution:
In an equation, imaginary roots occur in conjugate pairs.
Equation having roots α, β, γ, δ is (x – α) (x – β) (x – γ) (x – δ) = 0
Required equation is [x – (1 + 2i)] [x – (1 – 2i)] (x – 4) (x – 2) = 0
(x – (1 + 2i)] [x – (1 – 2i)] = [(x – 1) – 2i] [(x – 1) + 2i]
= (x – 1)2 – 4i2
= (x – 1)2 + 4
= x2 – 2x + 1 + 4
= x2 – 2x + 5
(x – 4) (x – 2) = x2 – 4x – 2x + 8 = x2 – 6x + 8
Required equation (x2 – 2x + 5) (x2 – 6x + 8) = 0
⇒ x4 – 2x3 + 5x2 – 6x3 + 12x2 – 30x + 8x2 – 16x + 40 = 0
⇒ x4 – 8x3 + 25x2 – 46x + 40 = 0
![]()
(iii) 2 ± √3, 1 ± 2i
Solution:
Required equation is [x – (2 + √3)] [x – (2 – √3)] [x – (1 + 2i)] [ x – (1 – 2i)] = 0
[x – (2 + √3)] [x – (2 – √3)]
= [(x – 2) – √3] [(x – 2) + √3]
= (x – 2)2 – 3
= x2 – 4x + 4 – 3
= x2 – 4x + 1
[x – (1 + 2i)] [x – (1 – 2i)] = [(x – 1) – 2i] [(x – 1) + 2i]
= (x – 1)2 – 4i2
= x2 – 2x + 1 + 4
= x2 – 2x + 5
Substituting in (1), the required equation is
(x2 – 4x + 1) (x2 – 2x + 5) = 0
⇒ x4 – 4x3 + x2 – 2x3 + 8x2 – 2x + 5x2 – 20x + 5 = 0
⇒ x4 – 6x3 + 14x2 – 22x + 5 = 0
(iv) 0, 0, 2, 2, -2, -2
Solution:
Required equation is (x – 0) (x – 0) (x – 2) (x – 2) (x + 2) (x + 2) = 0
⇒ x2 (x – 2)2 (x + 2)2 = 0
⇒ x2 (x2 – 4)2 = 0
⇒ x2 (x4 – 8x2 + 16) = 0
⇒ x6 – 8x4 + 16x2 = 0
(v) 1 ± √3, 2, 5
Solution:
Required equation is [x – (1 + √3)] [x – (1 – √3)][(x – 2) (x – 5)] = 0 ………(1)
[x – (1 + √3)] [x – (1 – √3)] = [(x – 1) – √3] [(x – 1) + √3]
= (x – 1)2 – 3
= x2 – 2x + 1 – 3
= x2 – 2x – 2
(x – 2) (x – 5) = x2 – 2x – 5x + 10 = x2 – 7x + 10
Substituting in (1), the required equation is
(x2 – 2x – 2) (x2 – 7x + 10) = 0
⇒ x4 – 2x3 – 2x2 – 7x3 + 14x2 + 14x + 10x2 – 20x – 20 = 0
⇒ x4 – 9x3 + 22x2 – 6x – 20 = 0
![]()
(vi) 0, 1, \(-\frac{3}{2}\), \(-\frac{5}{2}\)
Solution:
Required equation is

Question 2.
If α, β, γ are the roots of 4x3 – 6x2 + 7x + 3 = 0, then find the value of αβ + βγ + γα.
Solution:
α, β, γ are the roots of 4x3 – 6x2 + 7x + 3 = 0
α + β + γ = \(-\frac{a_{1}}{a_{0}}=\frac{6}{4}\)
αβ + βγ + γα = \(\frac{a_{2}}{a_{0}}=\frac{7}{4}\)
αβγ = \(-\frac{a_{3}}{a_{0}}=-\frac{3}{4}\)
∴ αβ + βγ + γα = \(\frac{7}{4}\)
Question 3.
If 1, 1, α are the roots of x3 – 6x2 + 9x – 4 = 0, then find α.
Solution:
1, 1, α are roots of x3 – 6x2 + 9x – 4 = 0
Sum = 1 + 1 + α = 6
⇒ α = 6 – 2 = 4
Question 4.
If -1, 2 and α are the roots of 2x3 + x2 – 7x – 6 = 0, then find α.
Solution:
-1, 2, α are roots of 2x3 + x2 – 7x – 6 = 0
Sum = -1 + 2 + α = \(-\frac{1}{2}\)
⇒ α = \(-\frac{1}{2}\) – 1 = \(-\frac{3}{2}\)
Question 5.
If 1, -2 and 3 are roots of x3 – 2x2 + ax + 6 = 0, then find a.
Solution:
1, -2 and 3 are roots of x3 – 2x2 + ax + 6 = 0
⇒ 1(-2) + (-2)3 + 3 . 1 = a
⇒ a = -2 – 6 + 3 = -5
![]()
Question 6.
If the product of the roots of 4x3 + 16x2 – 9x – a = 0 is 9, then find a.
Solution:
α, β, γ are the roots of 4x3 + 16x2 – 9x – a = 0
αβγ = 9
⇒ \(\frac{a}{4}\) = 9
⇒ a = 36
Question 7.
Find the values of s1, s2, s3, and s4 for each of the following equations.
(i) x4 – 16x3 + 86x2 – 176x + 105 = 0
(ii) 8x4 – 2x3 – 27x2 + 6x + 9 = 0
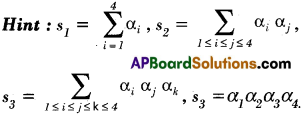
Solution:
(i) Given equation is x4 – 16x3 + 86x2 – 176x + 105 = 0
We know that

(ii) Equation is 8x4 – 2x3 – 27x2 + 6x + 9 = 0

II.
Question 1.
If α, β and 1 are the roots of x3 – 2x2 – 5x + 6 = 0, then find α and β.
Solution:
α, β and 1 are the roots of x3 – 2x2 – 5x + 6 = 0
Sum = α + β + 1 = 2
⇒ α + β = 1
product = αβ = -6
(α – β)2 = (α + β)2 – 4αβ
= 1 + 24
= 25
α – β = 5, α + β = 1
Adding
2α = 6
⇒ α = 3
α + β = 1
⇒ β = 1 – α
= 1 – 3
= -2
∴ α = 3 and β = -2
![]()
Question 2.
If α, β and γ are the roots of x3 – 2x2 + 3x – 4 = 0, then find
(i) Σα2β2
(ii) Σαβ(α + β)
Solution:
Since α, β, γ are the roots of x3 – 2x2 + 3x – 4 = 0 then
α + β + γ = 2
αβ + βγ + γα = 3
αβγ = 4
(i) Σα2β2 = α2β2 + β2γ2 + γ2α2
= (αβ + βγ + γα)2 – 2αβγ(α + β + γ)
= 9 – 2 . 2 . 4
= 9 – 16
= -7
(ii) Σαβ(α + β) = α2β + β2γ + γ2α + αβ2 + βγ2 + γα2
= (αβ + βγ + γα) (α + β + γ) – 3αβγ
= 2 . 3 – 3 . 4
= 6 – 12
= -6
Question 3.
If α, β and γ are the roots of x3 + px2 + qx + r = 0, then find the following.
(i) \(\sum \frac{1}{\alpha^{2} \beta^{2}}\)
(ii) \(\frac{\beta^{2}+\gamma^{2}}{\beta \gamma}+\frac{\gamma^{2}+\alpha^{2}}{\gamma \alpha}+\frac{\alpha^{2}+\beta^{2}}{\alpha \beta}\) or \(\Sigma \frac{\beta^{2}+\gamma^{2}}{\beta \gamma}\)
(iii) (β + γ – 3α) (γ + α – 3β) (α + β – 3γ)
(iv) Σα3β3
Solution:
α, β and γ are the roots of x3 + px2 + qx + r = 0,
α + β + γ = -p
αβ + βγ + γα = q
αβγ = -r

(iii) (β + γ – 3α) (γ + α – 3β) (α + β – 3γ) = (α + β + γ – 4α) (α + β + γ – 4β) (α + β + γ – 4γ)
= (-p – 4α) (-p – 4β) (-p – 4γ)
= -(p + 4α) (p + 4β) (p + 4γ)
= -(p3 + 4p2 (α + β + γ) + 16p (αβ + βγ + γα) + (64αβγ)
= -(p3 – 4p3 + 16pq – 64r)
= 3p3 – 16pq + 64r
(iv) Σα3β3 = α3β3 + β3γ3 + γ3α3
(αβ + βγ + γα)2 = α2β2 + β2γ2 + γ2α2 + 2αβγ (α + β + γ)
⇒ q2 = α2β2 + β2γ2 + γ2α2 + 2pr
⇒ α2β2 + β2γ2 + γ2α2 = q2 – 2pr
∴ α3β3 + β3γ3 + γ3α3 = (α2β2 + β2γ2 + γ2α2) (αβ + βγ + γα) – αβγ Σα2β
= (q2 – 2pr) . q + r[(αβ + βγ + γα) (α + β + γ) – 3αβγ]
= q3 – 2pqr + r(-pq + 3r)
= q3 – 2pqr – pqr + 3r2
= q3 – 3pqr + 3r2
![]()
III.
Question 1.
If α, β, γ are the roots of x3 – 6x2 + 11x – 6 = 0, then find the equation whose roots are α2 + β2, β2 + γ2, γ2 + α2.
Solution:
1st Method:
Let α, β, γ are the roots of the equation x3 – 6x2 + 11x – 6 = 0
∴ α + β + γ = 6, αβ + βγ + γα = 11
Let y = α2 + β2 = α2 + β2 + γ2 – γ2
⇒ y = (α + β + γ)2 – 2(αβ + βγ + γα) – x2
⇒ y = 36 – 22 – x2
⇒ x2 = 14 – y
⇒ x = \(\sqrt{14-y}\)
Substitute x = \(\sqrt{14-y}\) in x3 – 6x2 + 11x – 6 = 0
⇒ (\(\sqrt{14-y}\))3 – 6(\(\sqrt{14-y}\))2 + 11(\(\sqrt{14-y}\)) – 6 = 0
⇒ (14 – y) \(\sqrt{14-y}\) – 6(14 – y) + 11 \(\sqrt{14-y}\) – 6 = 0
⇒ -6(14 – y + 1) = \(\sqrt{14-y}\) [-11 – 14 + y]
⇒ -6(15 – y) = (\(\sqrt{14-y}\)) (y – 25)
Squaring on both sides
i.e., [-6(15 – y)]2 = [\(\sqrt{14-y}\)(y – 25)]2
⇒ 36(225 – 30y + y2) = (14 – y)(y2 – 50y + 625)
⇒ 8100 – 1080y + 36y2 = 14y2 – 700y + 8750 – y3 + 50y2 – 625y
⇒ 8100 – 1080y + 36y2 = -y3 + 64y2 – 1325y + 8750
⇒ y3 – 28y2 + 245y – 650 = 0
∴ The required equation is x3 – 28x2 + 245x – 650 = 0
2nd Method:
Let α, β, γ are the roots of x3 – 6x2 + 11x – 6 = 0
It is an odd-degree reciprocal equation of class two.
∴ x – 1 is a factor of x3 – 6x2 + 11x – 6
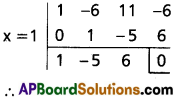
∴ x3 – 6x2 + 11x – 6 = (x – 1) (x2 – 5x + 6) = (x – 1) ( x – 2) (x – 3)
∴ The roots of x3 – 6x2 + 11x – 6 = 0 are α = 1, β = 2, γ = 3
Now α2 + β2 = 12 + 22 = 5
β2 + γ2 = 22 + 32 = 13
γ2 + α2 = 32 + 12 = 10
Therefore the cubic equation with roots α2 + β2, β2 + γ2, γ2 + α2 is (x – 5) (x – 13) (x – 10) = 0
⇒ x3 – (5 + 13 + 10) x2 + (65 + 130 + 50)x – 650 = 0
⇒ x3 – 28x2 + 245x – 650 = 0
![]()
Question 2.
If α, β, γ are the roots of x3 – 7x + 6 = 0, then find the equation whose roots are (α – β)2, (β – γ)2, (γ – α)2
Solution:
1st Method:
Let α, β, γ are the roots of the equation x3 – 7x + 6 = 0 …….(1)
α + β + γ = 0, αβγ = -6
Let y = (α – β)2 = (α + β)2 – 4αβ
⇒ y = (-γ)2 – 4(\(\frac{6}{\gamma}\))
⇒ y = γ2 + \(\frac{24}{\gamma}\)
⇒ y = x2 + \(\frac{24}{x}\)
⇒ xy = x3 + 24
⇒ xy = 7x – 6 + 24 [from (1)]
⇒ x(y – 7) = 18
⇒ x = \(\frac{18}{y-7}\)
Substituting x = \(\frac{18}{y-7}\) in x3 – 7x + 6 = 0
(\(\frac{18}{y-7}\))3 – 6(\(\frac{18}{y-7}\)) + 6 = 0
⇒ (18)3 – 7(18) (y – 7)2 + 6(y – 7)3 = 0
⇒ 5832 – 126(y2 – 14y + 49) + 6(y3 – 21y2 + 147y – 343) = 0
⇒ 972 – 21(y2 – 14y + 49) + (y3 – 21y2 + 147y – 343) = 0
⇒ y3 – 42y2 + 441y – 400 = 0
∴ The equation with roots (α – β)2, (β – γ)2, (γ – α)2 is x3 – 42x2 + 441x – 400 = 0
2nd Method:
α, β, γ are the roots of x3 – 7x + 6 = 0
By trial and error method x = 1 satisfies this equation.
∴ x – 1 is a factor of x3 – 7x + 6

∴ x3 – 7x + 6 = (x – 1) (x2 + x – 6) = (x – 1)(x + 3)(x – 2)
∵ α, β, γ are the roots of x3 – 7x + 6 = 0
α = 1, β = -3, γ = 2,
Now (α – β)2 = [1 – (-3)]2 = (4)2 = 16
(β – γ)2 = [-3 – 2]2 = 25
(γ – α)2 = [2 – 1]2 = 1
∴ The cubic equation whose roots are (α – β)2, (β – γ)2, (γ – α)2 is (x – 16) (x – 25) (x – 1) = 0
⇒ x3 – (16 + 25 + 1) x2 + (400 + 25 + 16)x – 400 = 0
⇒ x3 – 42x2 + 441x – 400 = 0
![]()
Question 3.
If α, β, γ are the roots of x3 – 3ax + b = 0, prove that Σ(α – β) (α – γ) = 9a.
Solution:
α, β, γ are the roots of x3 – 3ax + b = 0
∴ α + β + γ = 0, αβ + βγ + γα = -3a, αβγ = -b
Σ(α – β) (α – γ) = Σ[α2 – α(β + γ) + βγ]
= Σ[α2 + α2 + βγl
= 2(α2 + β2 + γ2) + (βγ + γα + αβ)
= 2(α + β + γ)2 – 4(αβ + βγ + γα) + (αβ + βγ + γα)
= 0 – 4(-3a) + (-3a)
= 9a