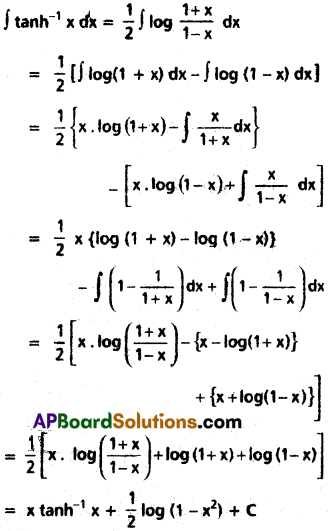Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Integration Solutions Exercise 6(c) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Integration Solutions Exercise 6(c)
I. Evaluate the following integrals.
Question 1.
∫x sec² x dx on I ⊂ R\{\(\frac{(2n+1)\pi}{2}\) : n is integer}.
Solution:
∫uvdx = u∫vdx – ∫[\(\frac{d}{du}\)(U).∫vdx]dx
Let v = sec² x and u = x then
∫x sec² x dx = x(tan x) – ∫tan x dx
= x tan x – log|sec x| + C
Question 2.
∫ex(tan-1 x + \(\frac{1}{1+x^2}\))dx, x ∈ R.
Solution:
∫ex[f(x) + f'(x)] dx = ex. f(x) + C
Let f(x) = tan-1 x so that f'(x) = \(\frac{1}{1+x^2}\)
∴ ∫ex(tan-1 x + \(\frac{1}{1+x^2}\))dx = extan-1 x + C
Question 3.
∫\(\frac{log x}{x^2}\) dx on (0, ∞).
Solution:
∫\(\frac{log x}{x^2}\) dx = (log x)(-\(\frac{1}{x}\)) + ∫\(\frac{1}{x}\) . \(\frac{1}{x}\)dx
= – \(\frac{1}{x}\)log x – \(\frac{1}{x}\) + C
Question 4.
∫(log x)² dx (0, ∞).
Solution:
∫(log x)² dx = (log x)² x – ∫x . 2log x.\(\frac{1}{x}\) dx
= x (log x)² – 2 ∫log x dx
= x (log x)² – 2(x . log x – ∫x\(\frac{1}{x}\)dx)
= x(log x)² – 2x. log x + 2x + c
Question 5.
∫ex(sec x + sec x . tan x)dx on I ⊂ R\{(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}.
Solution:
∫ex(sec x + sec x . tan x)dx = ex.sec x + C
[∫ex[f(x) + f'(x)]dx = ex f(x) + C]
![]()
Question 6.
∫ex cos x dx on R.
Solution:
I = ∫ex cos x dx = ex sin x – ∫sin x . ex dx
= ex. sin x + ex. cos x – ∫ex . cos x dx
= ex(sin x + cos x) – I
2I = ex(sin x + cos x)
I = \(\frac{e^x}{2}\)(sin x + cos x) + C
Question 7.
∫ex(sin x + cos x) dx on R.
Solution:
∫ex(sin x + cos x) dx
f(x) = sin x ⇒ f'(x) = cos x
∴ ∫ex(sin x + cos x) dx = ex. sin x + C
Question 8.
∫(tan x + log sec x)ex dx on ((2n – \(\frac{1}{2}\))π, (2n + \(\frac{1}{2}\))π) n ∈ Z.
Solution:
t = log|sec| ⇒ dt = \(\frac{1}{\sec x}\). sec x .tan x dx
= tan x dx
∫(tan x + log sec x)ex dx = ex.log|sec x| + C
II. Evaluate the following integrals.
Question 1.
∫xnlog x dx on (0, ∞), n is a real nember and n ≠ -1.
Solution:
∫xnlog x dx
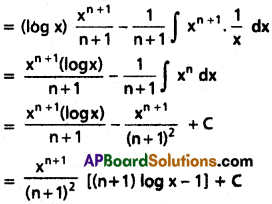
Question 2.
∫log (1 + x²) dx on R.
Solution:
∫log (1 + x²) dx on
= [log (1 + x²). x – ∫x\(\frac{1}{1+x^2}\)2x dx
= x log (1 + x²) – 2∫\(\frac{1+x^2-1}{1+x^2}\)dx
= x log (1 + x²) – 2∫dx + 2∫\(\frac{dx}{1+x^2}\)
= x log (1 + x²) – 2x + 2 tan-1 x + C
Question 3.
∫\(\sqrt{x}\) log x dx on (0, ∞).
Solution:
∫\(\sqrt{x}\) log x dx
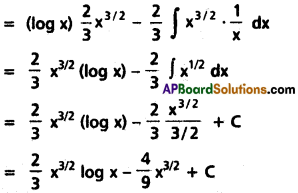
Question 4.
∫e√x dx on (0, ∞).
Solution:
t = √x ⇒ x = t²
dx = 2t dt
∫e√x dx = 2∫t et dt
= 2 [t et – ∫et dt
= 2 (t et – et) + C
= 2√x e√x – 2e√x + C
Question 5.
∫x² cos x dx on R.
Solution:
∫x² cosx dx = x²(sin x) – ∫sin x(2x dx)
= x² sin x + 2∫x(-sin x)dx
= x². sin x + 2[x cos x – ∫cos x dx]
= x² sin x + 2x cos x – 2 sin + C
![]()
Question 6.
∫x sin² x dx on R.
Solution:
∫x sin² x dx = \(\frac{1}{2}\)∫x(1 – cos 2x) dx
= \(\frac{1}{2}\)[∫x dx – ∫x cos 2x dx]
= \(\frac{1}{2}\)[\(\frac{x^2}{2}\) – {x . \(\frac{\sin 2x}{2}\) – \(\frac{1}{2}\)∫sin 2x dx}]
= \(\frac{x^2}{4}\) – \(\frac{x}{4}\)sin 2x + \(\frac{1}{4}\)∫sin 2x dx
= \(\frac{x^2}{4}\) – \(\frac{x}{4}\)sin 2x – \(\frac{1}{8}\)cos 2x + C
Question 7.
∫x cos² x dx on R.
Solution:
∫x cos² x dx = \(\frac{1}{2}\)∫x(1+ cos 2x)dx
= \(\frac{1}{2}\)[∫x dx + ∫x cos 2x dx]
= \(\frac{1}{2}\)[\(\frac{x^2}{2}\) + {x.\(\frac{\sin 2x}{2}\) – \(\frac{1}{2}\)∫sin 2x dx}]
= \(\frac{x^2}{4}\) + \(\frac{x}{4}\) sin 2x – \(\frac{1}{4}\) ∫sin 2x dx
= \(\frac{x^2}{4}\) + \(\frac{x}{4}\) sin 2x + \(\frac{1}{8}\)cos 2x + C
Question 8.
∫cos √x dx on R.
Solution:
t = x = t² ⇒ dx = 2t dt
I = 2∫t. cos t dt = 2 (t sin t – ∫sin t dt)
= 2(t sin t + cos t) + C
= 2√x sin √x + 2 cos√x + C
Question 9.
∫x sec² 2x dx on I ⊂ R\ {(2nπ + 1)\(\frac{\pi}{4}\) : n ∈ Z}.
Solution:
∫x sec² 2x dx = x\(\frac{\tan 2x}{2}\) – \(\frac{1}{2}\)∫tan 2x dx
= x\(\frac{\tan 2x}{2}\) – \(\frac{1}{2}\) . \(\frac{1}{2}\) log|sec 2x| + C
= x\(\frac{\tan 2x}{2}\) – \(\frac{1}{4}\) log|sec 2x| + C
Question 10.
∫x cot² x dx on I ⊂ R\{nπ : n ∈ Z}.
Solution:
∫x cot² x dx
= ∫x (cosec² x – 1)dx
= ∫x cosec²x dx – ∫x dx
= x (- cot x) + ∫cot x dx – \(\frac{x^2}{2}\)
= – x cot x + log|sin x| – \(\frac{x^2}{2}\) + C
Question 11.
∫ex(tan x + sec² x)dx on I ⊂ R\{(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}.
Solution:
f(x) = tan x ⇒ f'(x) = sec² x dx
I = ∫ex[f(x) + f'(x)] dx = ex. f(x) + C
= ex. tan x + C
Question 12.
∫ex(\(\frac{1+log x}{x}\))dx on (0, ∞).
Solution:
∫ex(\(\frac{1+log x}{x}\))dx = ∫ex(log x + \(\frac{1}{x}\))dx
= ex.log x + C
Question 13.
∫eaxsin bx dx on R, a, b ∈ R.
Solution:
Let I = ∫eaxsin bx dx …………. (1)

Question 14.
∫\(\frac{x.e^2}{(x+1)^2}\) dx on I ⊂ R\{-1}
Solution:
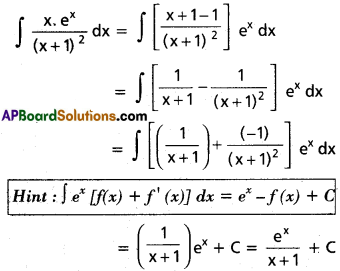
Question 15.
∫\(\frac{dx}{(x^2+a^2)^2}\), (a > 0) on R.
Solution:
Put x = tan t
Then dx = a sec² t dt

Question 16.
∫ex log (e2x + 5ex + 6) dx on R.
Solution:
∫ex log (e2x + 5ex + 6) dx
∵ e2x + 5ex + 6 = (ex + 2)(ex + 3)
= ∫ex. log((ex + 2)(ex + 3))dx
= ∫ex.{log(ex + 2) + log(ex + 3)}dx
= ∫exlog (ex + 2)dx + ∫exlog (ex + 3)dx
Put ex = t ⇒ exdx = dt
= ∫log(t + 2)dt + ∫log(t + 3) dt
= log(t + 2)∫1dt – ∫{\(\frac{d}{dt}\)log(t + 2). ∫1dt}dt + log(t + 3)∫1dt – ∫{\(\frac{d}{dt}\)log(t + 3). ∫1dt}dt
= t log(t + 2) – ∫\(\frac{1}{t + 2}\))t dt + t log(t+ 3) – ∫\(\frac{1}{t + 3}\)). t dt
= t {log(t + 2) + log (t + 3)} – ∫\(\frac{t}{t + 2}\)dt – ∫\(\frac{t}{t + 3}\)dt
= t log (t² + 5t + 6) – ∫(\(\frac{t+2-2}{t + 2}\))dt – ∫(\(\frac{t+3-3}{t + 3}\))dt
= t. log (t² + 5t + 6) – ∫{1 – \(\frac{2}{t + 2}\)}dt – ∫{1 – \(\frac{3}{t + 3}\)}dt
= t log (t² + 5t + 6) – t + 2 log|t + 2| – t + 3 log|t + 3| + C
= t log (t² + 5t + 6) – 2t + 2 log|t + 2| + 3log|t + 3| + C
= ex log(e2x + 5ex + 6) – 2ex + 2log ex + 2 + 3 log ex + 3 + C
![]()
Question 17.
∫ex.\(\frac{x+2}{(x+3)^2}\) dx on I ⊂ R\ {-3}
Solution:

Question 18.
∫cos (log x) dx on (0, ∞).
Solution:
Put log x = t
x = et
dx = et . dt
I = ∫et . cos t . dt
= et sin t – ∫sin.et dt
= et . sin t + cos t . et – ∫et . cos t dt
2I = et . (sin t + cos t)
I = \(\frac{e^t}{2}\)(sin t + cos t)
= \(\frac{x}{2}\)[sin(log x) + cos(log x)] + C
III. Evaluate the following integrals.
Question 1.
∫x tan-1 x dx, x ∈ R
Solution:
∫x tan-1 x dx = (tan-1 x)\(\frac{x^2}{2}\) – \(\frac{1}{2}\)∫x².\(\frac{1}{1+x^2}\)dx
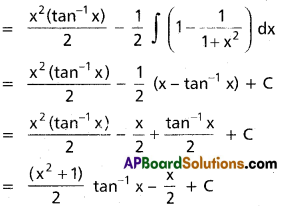
Question 2.
∫x² tan-1 x dx, x ∈ R.
Solution:

Question 3.
∫\(\frac{tan^{-1}x}{x^2}\) dx, x ∈ I ⊂ R\{0}
Solution:
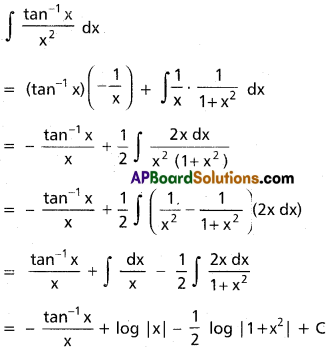
Question 4.
∫x cos-1x dx, x ∈ (-1, 1).
Solution:
∫x cos-1x dx
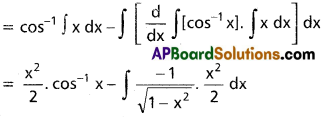

Question 5.
∫x² sin-1x dx, x ∈ (-1, 1).
Solution:
∫x² sin-1x dx

![]()
Question 6.
∫x log(1 + x) dx, x ∈ (-1, ∞).
Solution:
∫x log(1 + x) dx
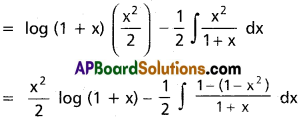

Question 7.
∫sin √x dx, on (0, ∞).
Solution:
x = t² ⇒ dx = 2t dt
∫sin √x dx = 2∫t. sin t dt
= 2(t(-cos t) + ∫cos t dt)
= -2t cos t + 2 sin t
= -2√x cos √x + 2 sin √x + C
Question 8.
∫eax sin (bx + c)dx, (a, b, c ∈ R, b ≠ 0) on R.
Solution:
Let I = ∫eax sin (bx + c)dx


Question 9.
∫ax cos 2x dx on R (a > 0 and a ≠ 0).
Solution:

Question 10.
∫tan-1(\(\frac{3x-x^3}{1-3x^2}\)) dx on I ⊂ R\{-\(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\)}.
Solution:
Put x = tan t ⇒ dx = sec² t dt
Then
∫tan-1(\(\frac{3x-x^3}{1-3x^2}\)) dx
= ∫tan-1(\(\frac{3 \tan t -\tan^3 t}{1-3\tan^2 t}\)) dx
= ∫tan-1(tan 3t).sec² t dt
= 3∫t sec² t dt
= 3[t∫sec² t dt – ∫{\(\frac{d}{dt}\)(t) ∫sec² t dt}dt]
= 3[t(tan t) – ∫(1) tan t dt]
= 3(x tan-1 x – log\(\sqrt{1+x^2}\)) + C
= 3x[tan-1 x – \(\frac{3}{2}\)log (1 + x²) + C
= 3x tan-1(x) – \(\frac{3}{2}\)log (1 + x²) + C
Question 11.
∫sinh-1 x dx on R.
Solution:

Question 12.
∫cosh-1 x dx on (1, ∞).
Solution:

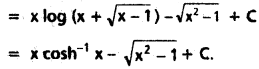
![]()
Question 13.
∫tanh-1x dx on (-1, 1).
Solution: