Inter 2nd Year Maths 2B Differential Equations Solutions Ex 8(c)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(c)

I.

Question 1.
Express x dy – ydx = \(\sqrt{x^2+y^2}\) dx in the form F (\(\frac{y}{x}\)) = (\(\frac{dy}{dx}\)).
Solution:
x. dy – y dx = \(\sqrt{x^2+y^2}\) dx
\(\frac{dy}{dx}\) – y = \(\sqrt{x^2+y^2}\)

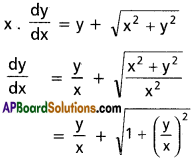
Question 2.
Express (x – y Tan^-1 \(\frac{y}{x}\))dx + x Tan^-1\(\frac{y}{x}\) dy = 0 in the form F(\(\frac{y}{x}\)) = \(\frac{dy}{dx}\).
Solution:

Question 3.
Express x\(\frac{dy}{dx}\) = y(log y – log x + 1) in the from F (\(\frac{y}{x}\)) = \(\frac{dy}{dx}\)
Solution:
x . \(\frac{dy}{dx}\) = y(log y – log x + 1)
\(\frac{dy}{dx}\) = \(\frac{y}{x}\)(log\(\frac{y}{x}\) + 1)

II. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=\frac{x-y}{x+y}\)
Solution:
\(\frac{dy}{dx}=\frac{x-y}{x+y}\)
Put y = vx
\(\frac{dy}{dx}\) = v + x\(\frac{dv}{dx}\)

Question 2.
(x² + y²) dy = 2xy dx
Solution:
(x² + y²) dy = 2xy dx

1 + v² = A(1 – v²) + Bv(1 – v) + Cv(1 + v)
v = 0 ⇒ = A
v = 1 ⇒ 1 + 1 = C(2) ⇒ c = 1
v = -1 ⇒ 1 + 1 = B(-1) (2) ⇒ 2 = -2B
B = -1

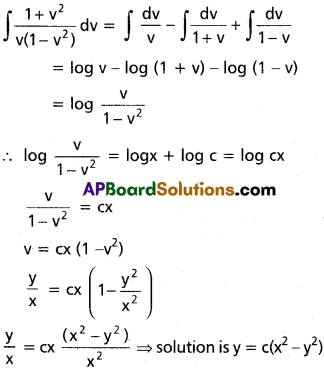
Question 3.
\(\frac{dy}{dx}=\frac{-(x^2+3y^2)}{3x^2+y^2}\)
Solution:
\(\frac{dy}{dx}=\frac{-(x^2+3y^2)}{3x^2+y^2}\)
Put y = vx

Multiplying with (v + 1)³
3 + v² = A(v + 1)² + B(v + 1) + C
v = – 1 ⇒ 3 + 1 = C ⇒ C = 4
Equating the co-efficients of v²
A = 1
Equating the co-efficients of v
0 = 2A + B
B = -2A = -2

Question 4.
y²dx + (x² – xy)dy = 0
Solution:

v – log v = log x + log k
v = log v + log x + log k
= log k (vx)
\(\frac{y}{x}\) = log ky
Solution is ky = e^y/x

Question 5.
\(\frac{dy}{dx}=\frac{(x+y)^2}{2x^2}\)
Solution:

Question 6.
(x² – y²)dx – xy dy = 0
Solution:
(x² – y²)dx – xy dy = 0
(x² – y²)dx = xy . dy

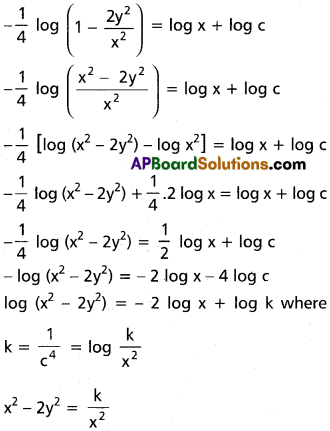
Question 7.
(x²y – 2xy²)dx = (x³ – 3x²y)dy
Solution:
(x²y – 2xy²)dx = (x³ – 3x²y)dy

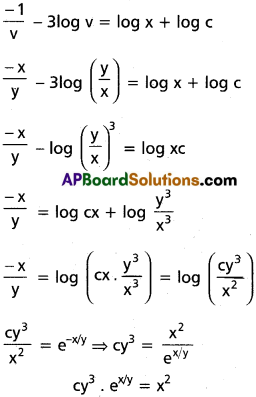
Question 8.
y²dx + (x² – xy + y²) dy = 0
Solution:
y²dx = – (x² – xy + y²)dy

1 – v + v² = A(1 + v²) + (Bv + C)v
v  =  0 ⇒ 1 = A
Equating the co-efficients of v²
1 = A + .B ⇒ B = 0
Equating the co-efficients of v
-1 = C

Question 9.
(y² – 2xy)dx + (2xy – x²)dy = 0
Solution:
(y² – 2xy)dx + (2xy – x²)dy = 0
(2xy – x²)dy = – (y² – 2xy)dx

2v – 1 = A(1 – v) + Bv
v = 0 ⇒ -1 = A ⇒ A = -1
v = 1 ⇒ 1 = B ⇒ B = 1

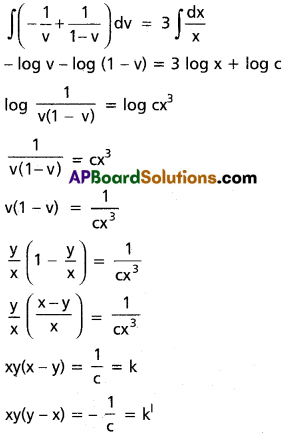
Question 10.
\(\frac{dy}{dx}+\frac{y}{x}=\frac{y^2}{x^2}\)
Solution:
\(\frac{dy}{dx}+\frac{y}{x}=\frac{y^2}{x^2}\)

Question 11.
x dy – y dx = \(\sqrt{x^2+y^2}\)
Solution:
x dy – y dx = \(\sqrt{x^2+y^2}\)

Question 12.
(2x – y)dy = (2y – x)dx
Solution:


⇒ (y – x)² = c²(y + x)²(y² – x²)
⇒ y – x = c²(y + x)³
⇒ (x + y)³ = c(x – y) where c = \(\frac{-1}{c^2}\)
∴ (x + y)³ = c(x – y)

Question 13.
(x² – y²)\(\frac{dy}{dx}\) = xy
Solution:

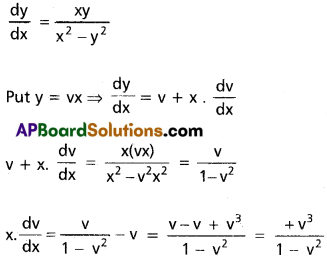
Question 14.
2\(\frac{dy}{dx}=\frac{y}{x}+\frac{y^2}{x^2}\)
Solution:
Put y = vx

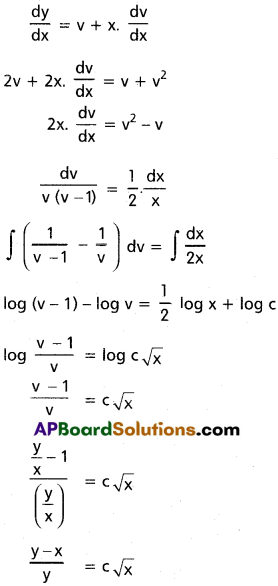
(y – x)² = y²c²x
Solution is y²x = c(x – y)²

III.

Question 1.
Solve : (1 + e^x/y)dx + e^x/y(1 – \(\frac{x}{y}\))dy = 0.
Solution:
Put x = vy

Question 2.
Solve : x sin \(\frac{y}{x}.\frac{dy}{dx}\) = y sin \(\frac{y}{x}\) – x
Solution:
Dividing with x, we have

Question 3.
Solve : x dy = (y + x cos² \(\frac{y}{x}\))dx
Solution:
x.\(\frac{dy}{dx}\) = y + xcos² \(\frac{y}{x}\)

Question 4.
Solve : (x – y log y + y log x)dx + x(log y – log x)dy = 0
Solution:
Dividing with x. dx we get

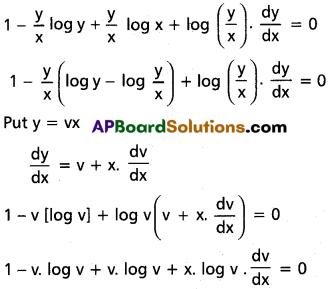
Question 5.
Solve : (y dx + x dy) x cos \(\frac{y}{x}\) = (x dy – y dx) y sin \(\frac{y}{x}\).
Solution:
The given equation can be written as

∴ This is a homogeneous equation

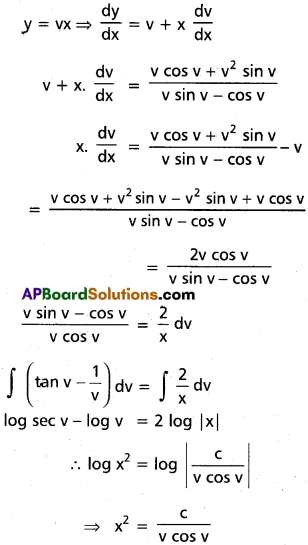
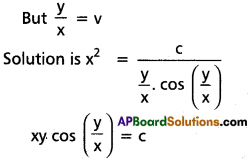
Question 6.
Find the equation of a curve whose gradient is \(\frac{dy}{dx}=\frac{y}{x}-\cos^2\frac{y}{x}\), where x > 0, y > 0 and which passes through the point (1, \(\frac{\pi}{4}\)).
Solution:

tan v = – log |x| + c
This curve passes through (1, \(\frac{\pi}{4}\))
tan \(\frac{\pi}{4}\) = c – log 1
c = 1
∴ Equation of the curve is
tan v = 1 – log |x|
tan \(\frac{y}{x}\) = 1 – log |x|