Mahesh

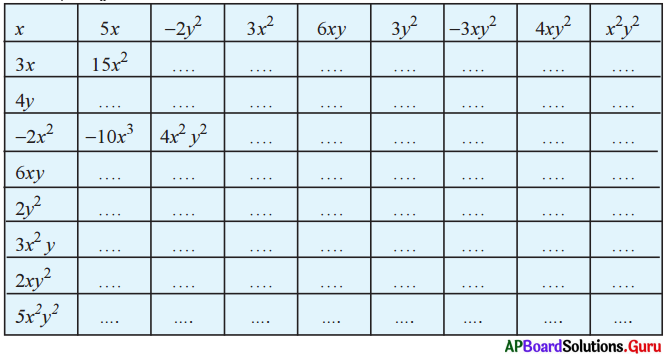
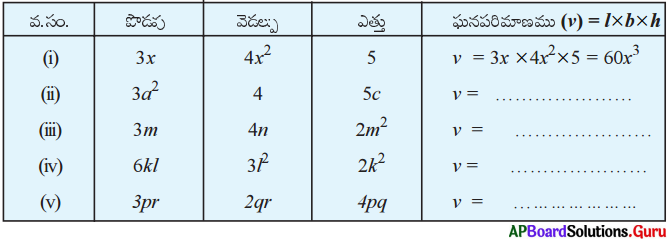
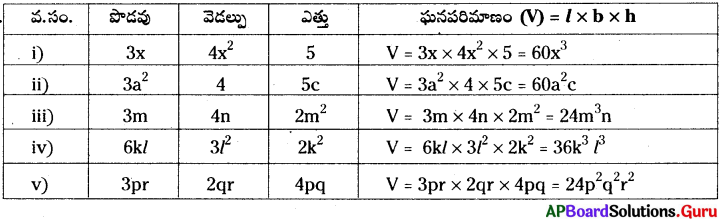
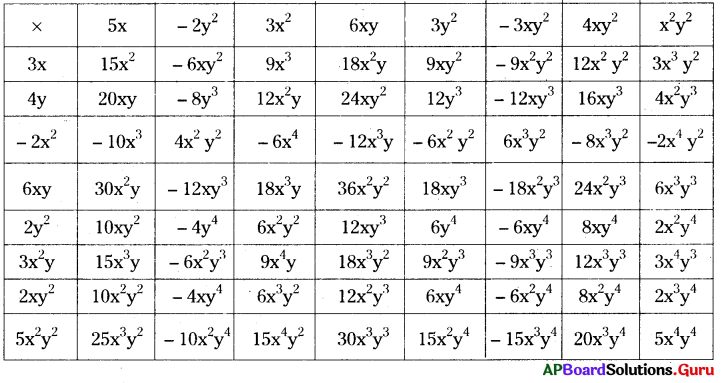AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.4

ప్రశ్న 1.
25110, 45చే భాగింపబడునో, లేదో సరిచూడండి.
సాధన.
ఇచ్చిన సంఖ్య = 25110
25110, 45తో భాగింపబడాలంటే అది 5, 9చే భాగింపబడవలెను.

గమనిక : 5చే భాగింపబడవలెనన్న ఇచ్చిన సంఖ్య యొక్క ఒకట్ల స్థానంలోని అంకె ‘0’ లేదా 5 అయి ఉండవలెను, 9చే ఒక సంఖ్య భాగింపబడవలెనన్న సంఖ్యలోని అంకెల మొత్తం 9చే భాగింపబడవలెను.
∴ 25110, 45చే భాగింపబడును.

ప్రశ్న 2.
61479, 81చే భాగింపబడునో, లేదో సరిచూడండి.
సాధన.
61479, 81చే భాగింపబడవలెనన్న అది 9చే భాగింపబడవలెను.
ఒక సంఖ్య ‘9’ చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం 19 చే భాగింపబడవలెను.
∴ 61479 → 6 + 1 + 4 + 7 + 9 → \(\frac {27}{9}\) (R = 0)
∴ 61479, 9 చే భాగింపబడును. (3, 9, 27, 81 లచే కూడా భాగింపబడును)

ప్రశ్న 3.
864, 36చే భాగింపబడుతుందో లేదో తెలపండి. మరియు 36 యొక్క కారణాంకములన్నింటిచే 864 భాగింపబడునో, లేదో పరిశీలించండి.
సాధన.
864, 36చే భాగింపబడవలెనన్న 36 యొక్క కారణాంకాలన్నింటిదే భాగింపబడవలెను.
36 యొక్క కారణాంకాలు = 1, 2, 3, 4, 6, 9, 12, 18, 36
864 = 864 → \(\frac {4}{2}\)(R = 0) ‘2’ చే భాగింపబడును.
864 → 8 + 6 + 4 → \(\frac {18}{3}\)(R = 0) ‘3’ చే భాగింపబడును.
864 అనునది 2 మరియు 3 లచే భాగింపబడును కావునా 6చే కూడా భాగింపబడును.
864 = 864 → \(\frac {64}{4}\)(R = 0) ‘4’ చే భాగింపబడును.
864 అనునది 3 మరియు 4 లచే భాగింపబడును కావునా 12చే కూడా భాగింపబడును.
864 → 8 + 6 + 4 → \(\frac {18}{9}\)(R = 0) 9చే భాగింపబడును.
864 అనునది 2 మరియు 9 లతో భాగింపబడును కావున 18చే కూడా భాగింపబడును.
∴ 864 అనునది 4 మరియు 9 లచే భాగింపబడును. కావున ఇది 36చే భాగింపబడును,
∴ 864 అనునది 36 యొక్క కారణాంకములన్నిందిచే భాగింపబడుతుంది.

ప్రశ్న 4.
756, 42చే భాగింపబడుతుందో లేదో తెలపండి. మరియు 42 యొక్క కారణాంకములన్నింటిచే 756 భాగింపబడునో, లేదో తెలపండి.
సాధన.
756, 42చే భాగింపబడవలెనన్న 6 మరియు 7చే భాగింపబడవలెను.
756, 6చే భాగింపబడవలెనన్న అది 2 మరియు 3చే భాగింపబడవలెను.
756 → \(\frac {6}{2}\)(R = 0) ‘2’ చే భాగింపబడుతుంది.
756 → 7 + 5 + 6 → \(\frac {18}{3}\)(R = 0) 3 చే భాగింపబడుతుంది.
756 ⇒ a = 7, b = 5, c = 6
2a + 3b + c = 2 × 7 + 3 × 5 + 6 = 14 + 15 + 6 → \(\frac {35}{7}\)(R = 0)
∴ 756 అనునది 6, 7 లచే భాగింపబడును. కావున ఇది 42చే భాగింపబడును.
756, 2 మరియు 7లచే భాగింపబడుతుంది కావున 14చే భాగింపబడును.
756, 3 మరియు 7 లచే భాగింపబడుతుంది కావున 21చే భాగింపబడుతుంది.
∴ 756, 42 యొక్క కారణాంకాలన్నింటిచే (1, 2, 3, 6, 7, 14, 21, 42) భాగింపబడుతుంది.

ప్రశ్న 5.
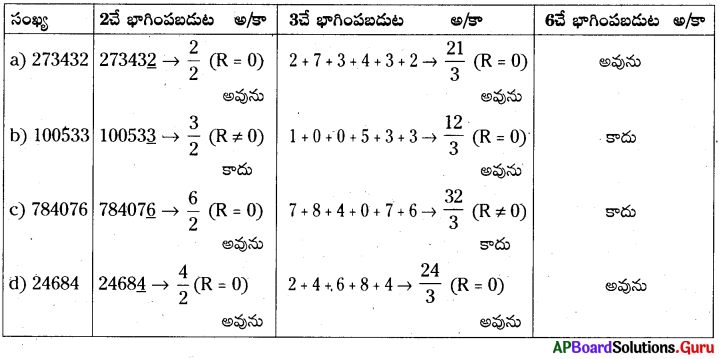
2156, 11 మరియు 7లచే భాగింపబడునో, లేదో చూడండి. మరియు 2156, 11 మరియు 7 ల యొక్క లబ్దంతో భాగింపబడుతుందో, లేదో పరిశీలించండి.
సాధన.

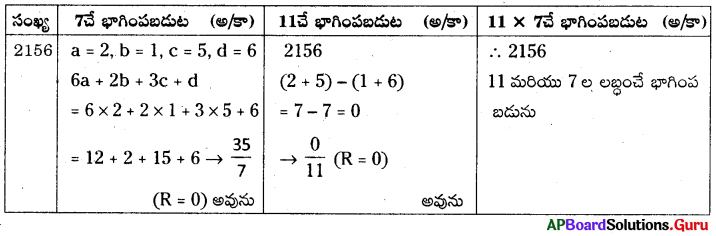
ప్రశ్న 6.
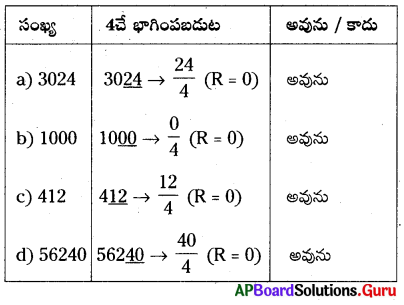
1435, 5 మరియు 7 లచే భాగింపబడునో, లేదో చూడండి. మరియు 1435, 5 మరియు 7ల యొక్క లబ్దంతో భాగింప బడునో, లేదో పరిశీలించండి.
సాధన.

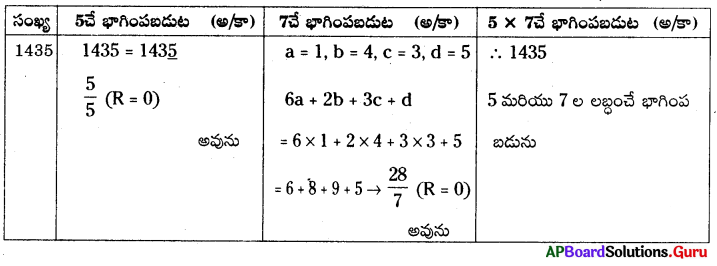
ప్రశ్న 7.
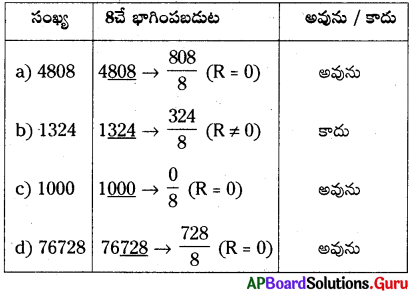
458, 618 సంఖ్యలు అదే భాగింపబడునో, లేదో పరిశీలించండి. మరియు వాటి మొత్తము కూడా 6దే భాగింపబడుతుందో, లేదో తెలపండి.
సాధన.

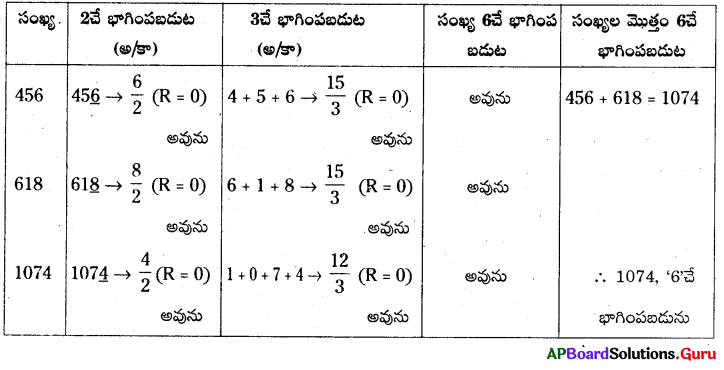
ప్రశ్న 8.
876, 345 లు 3తో భాగింపబడునో లేదో తెలపండి. మరియు వాటి భేదము కూడా 3తో భాగింపబడుతుందో లేదో తెలపండి.
సాధన.

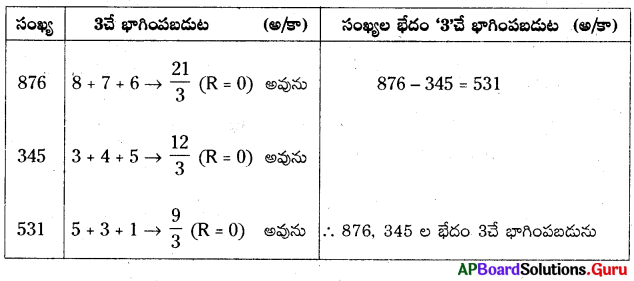
ప్రశ్న 9.
2² + 2³ + 2⁴; 2, 4 లేదా రెండింటితోను భాగింపబడుతుందో లేదో తెలపండి.
సాధన.

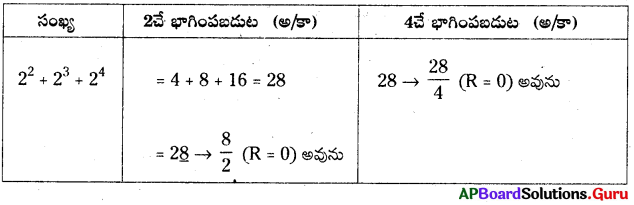
∴ 28 లేదా (2² + 2³ + 2⁴) అనునది 2, 4 మరియు రెండింటితోనూ భాగింపబడుతుంది.

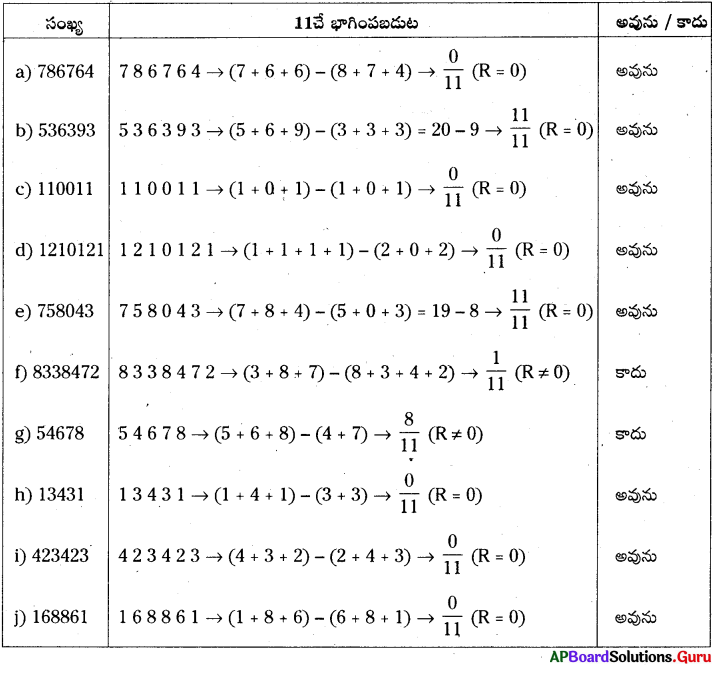
ప్రశ్న 10.
32², 4 లేదా 8 లేదా రెండింటితోను భాగింపబడుతుందో లేదో తెలపండి.
సాధన.

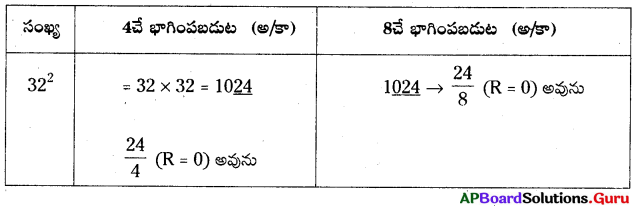
∴ 32², 4 లేదా 8 మరియు రెండింటిచే భాగింపబడును.

ప్రశ్న 11.
A679B, 72 తో నిశ్శేషముగా భాగింపబడిన A, B విలువలు కనుక్కోండి.
సాధన.
A679B, 72 చే నిశ్శేషంగా భాగింపబడవలెనన్న ఆ సంఖ్య 8 మరియు 9చే నిశ్శేషంగా భాగింపబడవలెను.
A6798, 9 చే భాగింపబడవలెనన్న
A + 6 + 7 + 9 + B = A + B + 22 = 27 (9 × 3)
⇒ A + B = 5 …………………(1)
A6 79B → \(\frac {79B}{8}\)
B = [2, 4, 6, 8] నుండి B = 2 అయిన
= \(\frac {792}{8}\) (R = 0)
∴ B = 2
(1) నుండి ⇒ A + 2 = 5
⇒ A = 3
∴ A = 3, B = 2

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.3

ప్రశ్న 1.
కింది సంఖ్యలు ‘6’తో భాగింపబడునో, లేదో భాజనీయతా నియమముల ఆధారంగా తెలపండి.
(a) 273432 (b) 100533 (c) 784076 (d) 24684
సాధన.

ప్రశ్న 2.
కింది సంఖ్యలు ‘4’తో భాగింపబడునో, లేదో భాజనీయతా నియమముల ఆధారంగా తెలపండి.
(a) 3024 (b) 1000 (c) 412 (d) 56240
సాధన.

ప్రశ్న 3.
భాజనీయతా నియమముల ఆధారంగా కింది సంఖ్యలు ‘8’ తో భాగింపబడునో లేదో తెలపండి.
(a) 4808 (b) 1324 (c) 1000 (d) 76728
సాధన.
ఒక సంఖ్య ‘8’చే భాగింపబడవలెనన్న సంఖ్యలోని చివరి మూడంకెలు ‘8’చే భాగింపబడవలెను.

ప్రశ్న 4.
భాజనీయతా నియమముల ఆధారంగా కింది సంఖ్యలు ‘7’ తో భాగింపబడునో లేదో తెలపండి.
(a) 427 (b) 3514 (c) 861 (d) 4676
సాధన.

ప్రశ్న 5.
ఈ కింది సంఖ్యలు ’11’తో భాగింపబడునో, లేదో భాజనీయతా నియమాల ఆధారంగా చెప్పండి.
(a) 786764
(b) 536393
(c) 110011
(d) 1210121
(e) 758043
(f) 8338472
(g) 54678
(h) 13431
(i) 423423
(j) 168861
సాధన.

ప్రశ్న 6.
ఒక సంఖ్య ‘8’తో భాగింపబడిన, ‘4’తో కూడా భాగింపబడును. వివరించండి.
సాధన.
ఒక సంఖ్య 8చే భాగింపబడిన అది 4తో కూడా భాగింపబడును.
ఎందుకనగా ఒక సంఖ్య 8చే భాగింపబడిన అది 8 యొక్క కారణాంకాలన్నింటిచే (1, 2, 4, 8) భాగించబడుతుంది.
∴ 4, 8కి ఒక కారణాంకం కావున
8చే భాగించబడే ప్రతి సంఖ్య, 4చే కూడా భాగించబడుతుంది.

ప్రశ్న 7.
ఒక మూడు అంకెల సంఖ్య 4A3, మరొక మూడు అంకెల సంఖ్య 984 కు కలుపగా ఏర్పడు సంఖ్య 13B7. ఈ సంఖ్య 11చే నిశ్శేషముగా భాగింపబడు తుంది. అయిన (A + B) కనుక్కోండి. .
సాధన.
ఇచ్చిన మూడంకెల సంఖ్యలు = 4A3, 984
∴ 4A3 + 984 = 13B7. ఇది 11 చే నిశ్శేషంగా భాగింపబడిన
⇒ 1 3 B 7
(1 + B) – (3 + 7)
⇒ (B + 1) – 10 = 0 ⇒ B – 9 = 0
∴ B = 9

⇒ A + 8 = 9 ⇒ A = 9 – 8 = 1
∴ A = 1
∴ A + B = 1 + 9 = 10

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.2

ప్రశ్న 1.
345 A 7, 3 తో నిశ్శేషముగా భాగింపబడిన ‘A’ యొక్క విలువ కనుగొనుము.
సాధన.
ఒక సంఖ్య 3చే నిశ్శేషముగా భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం ‘3’ చే భాగింపబడవలెను.
∴ 345A7 → 3 + 4 + 5 + A + 7 = 3 × 7 → 19 + A = 21
A + 19 = 3 × 8 అయిన
⇒ A = 24 – 19 = 5
A = 5
A + 19 = 3 × 9
A = 27 – 19
A = 8
∴ A = 21 – 19 = 2
A = 2
∴ A = {2, 5, 8} అగును.

ప్రశ్న 2.
2791A, 9 తో నిశ్శేషముగా భాగింపబడిన ‘A’ యొక్క విలువ కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘9’చే నిశ్శేషంగా భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం ‘9’ చే భాగింపబడవలెను.
∴ 2791A → 2 + 7 + 9 + 1 + A = 9 × 3
⇒ 19 + A = 9 × 3= 27
⇒ A = 27 – 19 = 8
∴ A = 8

ప్రశ్న 3.
2, 3, 5, 9 మరియు 10తో నిశ్శేషముగా భాగింపబడు కొన్ని సంఖ్యలు పేర్కొనండి.
సాధన.
2, 3, 5, 9 మరియు 10లతో భాగింపబడు సంఖ్యలు 90, 180, 270, 360, 450, ……..

ప్రశ్న 4.
2A8 అను సంఖ్య 2తో నిశ్శేషముగా భాగింపబడిన, Aకు ఎన్ని విలువలు ఉండవచ్చు. ? ఏమి గమనించితిరి ?
సాధన.
2A8 అను సంఖ్య ‘2’చే నిశ్శేషంగా భాగింపబడవలెనన్న ఒకట్ల స్థానంలోని అంకె 0, 2, 4, 6, 8 అయి ఉండి మిగిలిన
పదుల స్థానంలోని అంకె ఏదైనా ఉండవచ్చు.
∴ A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

ప్రశ్న 5.
50B, 5తో నిశ్శేషముగా భాగింపబడిన, B కు గల విలువలు కనుక్కోండి.
సాధన.
ఇచ్చిన సంఖ్య = 50B
ఒక సంఖ్య ‘5’చే నిశ్శేషంగా భాగింపబడవలెనన్న అందు ఒకట్ల స్థానంలోని అంకె ‘0’ లేదా ‘5’ అయి ఉండాలి.
⇒ B = {0, 5}
∴ 500 → \(\frac {0}{5}\) (R = 0)
505 → \(\frac {5}{5}\) (R = 0)
∴ B = 0 లేదా 5 అయిన 50B ‘5’చే నిశ్శేషంగా భాగింపబడును.

ప్రశ్న 6.
2P అను సంఖ్య 2తో, 3తో నిశ్శేషముగా భాగింపబడిన, P విలువ కనుక్కోండి.
సాధన.
ఇచ్చిన సంఖ్య = 2P
2తో, 3తో భాగింపబడవలెనన్న
P = 4 కావలెను [∵ 2 + P = 6 ⇒ P = 6 – 2 = 4)
∴ 2P = 24 → \(\frac {4}{2}\)(R = 0)
24 → 2 + 4 → \(\frac {6}{3}\)(R = 0)
∴ P = 4 కావలెను.

ప్రశ్న 7.
54z ను 5 తో భాగించిన 2 శేషము వచ్చును మరియు 3తో భాగించినపుడు 1 శేషం వచ్చును. అయిన ‘Z’ విలువ కనుగొనండి.
సాధన.
54z ను 3తో భాగించిన శేషం 1 వచ్చు సందర్భంలో
⇒ 5 + 4 + Z = (3 × 4) + 1
9 + z = 13
Z = 13 – 9 = 4 లేదా
9 + Z = (3 × 5) + 1 ⇒ 9 + z = 16 ⇒ z = 7
54z, 5 తో భాగింపబడవలెనన్న ఒకట్ల స్థానంలోని అంకె 0 లేదా 5 అయి ఉండవలెను.
= 54(0 + 2) = 542 (Z = 2)
54 (0 + 7) = 547 (Z = 7)
∴ పై రెండు సందర్భాల నుండి Z = 7 అగును.

ప్రశ్న 8.
27Q ను 5తో భాగించినపుడు 3 శేషము, 2తో భాగించినపుడు 1 శేషం వచ్చును. అయిన 3తో భాగించినపుడు వచ్చు శేషము కనుగొనుము.
సాధన.
27Q, 5 చే భాగించబడిన శేషం 3 వచ్చే సందర్భాలు
27Q = 27(0 + 3) = 273 (Z = 3) (T)
= 27 (0 + 8) = 278 (Z = 8)
27Q, 2చే భాగింపబడినపుడు శేషం 1 వచ్చు సందర్భాలు
27Q = 27(0 + 1) = 271 (Z = 1)
27Q = 27 (0 + 3) = 273 (Z = 3)(T)
∴ పై రెండు సందర్భాల నుండి Z = 3 అగును.
∴ 27Q = 273 → 2 + 7 + 3 → \(\frac {12}{3}\)(R= 0)
∴ 273, 3 చే భాగింపబడినపుడు శేషం ‘0’ అగును.

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.1

ప్రశ్న 1.
భాజనీయతా సూత్రములుపయోగించి, క్రింది పట్టికలో ఇవ్వబడిన అంకెలు 2, 5, 10 తో నిశ్శేషముగా భాగింపబడిన అవును అని, భాగింపబడని కాదు అని వ్రాయండి.

సాధన.

ప్రశ్న 2.
భాజనీయతా నియమము ద్వారా క్రింది సంఖ్యలలో ఏవి ‘2’ తో భాగింపబడునో తెలపండి.
(a) 2144
(b) 1258
(c) 4336
(d) 633
(e) 1352
సాధన.
ఒక సంఖ్య ‘2’ చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె 0, 2, 4, 6, 8 అయి ఉండవలెను,
(a) 2144
(b) 1252
(c) 433
(d) 1352 లు “2 చే భాగింపబడును.

ప్రశ్న 3.
భాజనీయతా నియమము ద్వారా కింది సంఖ్యలలో ఏవి ‘5″ తో భాగింపబడునో తెలపండి.
(a) 438750
(b) 179015
(c) 125
(d) 639210
(e) 17852
సాధన.
ఒక సంఖ్య 5’చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంతె 0 లేదా 5 అయి ఉండవలెను.
(a) 438750
(b) 179015
(c) 125
(d) 639210 లు ‘5’చే భాగింపబడును.

ప్రశ్న 4.
భాజనీయతా నియమము ద్వారా కింది సంఖ్యలలో ఏవి ’10’ తో భాగింపబడునో తెలపంది.
(a) 54450
(b) 10800
(c) 7138965
(d) 7016930
(e) 10101010
సాధన.
ఒక సంఖ్య ’10’చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె 0 (సున్నా) అయి ఉండవలెను.
(a) 54450
(b) 1080
(d) 7016930
(e) 10101010 లు ’10 చే భాగింపబడును.

ప్రశ్న 5.
కింది సంఖ్యలకు కారణాంకాల సంఖ్యను కనుగొనండి.
(a) 18 (b) 24 (c) 45 (d) 90 (e) 105
సాధన.

ప్రశ్న6.
2, 5 మరియు 10తో భాగింపబడే ఏవైనా 5 సంఖ్యలను తెలపండి.
సాధన.
2, 5 మరియు 10తో భాగింపబడే సంఖ్యలు 10, 20, 30, 40, 50 ……..

ప్రశ్న 7.
34A అను సంఖ్య ‘2’తో నిశ్శేషముగా భాగింపబడును. 5తో భాగింపబడిన శేషము ‘1’ అయిన ‘A’ విలువ కనుగొనుము.
సాధన.
34A, 2చే భాగింపబడిన శేషం 0 కావలెనన్న (A = (0, 2, 4, 6, 8 కావలెను)
∴ 340, 342, 344, 346, 348 లలో 5చే భాగించగా శేషం ‘1’ వచ్చు సంఖ్య 346
∴ 346 → \(\frac {6}{5}\) (R = 1)
∴ కావలసిన A విలువ 6.

AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము) InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం InText Questions

ఇవి చేయండి

1. ఈ క్రింది దీర్ఘఘనముల యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 298)

సాధన.
(i) l = 4 సెం.మీ., b = 4 సెం.మీ., h = 10 సెం.మీ.
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)
= 2(4 × 4 + 4 × 10 + 4 × 10)
= 2(16 + 40 + 40)
= 2 × 96 = 192 చ.సెం.మీ.
(ii) l = 6 సెం.మీ., b = 4 సెం.మీ., h = 2 సెం.మీ.
దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)
= 2 (6 × 4 + 4 × 2+ 6 × 2)
= 2 (24 + 8 + 12)
= 2 × 44 = 88 చ.సెం.మీ.

2. 6 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ. కొలతలుగా గల దీర్ఘఘనము యొక్క ఘనపరిమాణమును కనుక్కోండి. (పేజీ నెం. 305)

ఒక ఘనపు భుజము సెం.మీ. గా గల ప్రమాణ ఘనములను దీర్ఘఘనము పొడవు వెంబడి పేర్చుము. దీని కొరకు మనకు ఎన్ని ఘనములు అవసరము ? 6 ప్రమాణ ఘనములు అవసరము. వెడల్పు వెంబడి ఎన్ని ప్రమాణు ఘనములు పేర్చవచ్చు ? 4 ప్రమాణ ఘనములు దీనికి గల కారణము దీర్ఘ ఘనము యొక్క వెడల్పు 4 సెం.మీ. అనగా ఒక పారలో 6 × 4 ప్రమాణ ఘనములు ఉంటాయి.

దీర్ఘ ఘనములో ప్రమాణ ఘనములు అమర్చే పొరలు ఎన్ని ? 5 పొరలు అనగా దీర్ఘఘనము యొక్క ఎత్తు 5 సెం.మీ. ప్రతి పౌర 6 × 4 ఘనములు కలవు. కావున 5 పొరలలో 6 × 4 × 5 ప్రమాణ సమఘనాల దిమ్మలు ఉంటాయి. అనగా l × b × hకు సమానం.
పై చర్చ దీర్ఘఘనము యొక్క ఘనపరిమాణమునకు సూత్రము నిచ్చును.
దీర్ఘఘన ఘనపరిమాణము = పొడవు × వెడల్పు × ఎత్తు
సాధన.
6 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ. కొలతలు గల దీర్ఘ ఘనం యొక్క ఘనపరిమాణం
V= lbh ⇒ V = 6 × 4 × 5 ⇒ V = 120 సెం.మీ³

3. 64 ప్రమాణ ఘనములను ఉపయోగించి మీరు ఏర్పరచగల దీర్ఘఘనములు ఎన్ని ? ప్రతీ అమరిక యొక్క సంపూర్ణతల వైశాల్యము కనుక్కోండి. సమాన ఘనపరిమాణము కలిగిన ఘనముల యొక్క ప్రక్కతల వైశాల్యములు సమానమేనా ? (పేజీ నెం. 306)
సాధన.
64 ప్రమాణ ఘనములను ఉపయోగించి మీరు ఏర్పరచగల దీర్ఘఘనాల సంఖ్య
64 = 1 × 64 ……….. (1)
= 2 × 32 ………………… (2)
= 4 × 16 ………………….. (3)
ఈ విధంగా 3 విధాలుగా దీర్ఘఘనాలను ఏర్పర్చవచ్చు.
1. l = 64 సెం.మీ. , b = 1 సెం.మీ., h = 1 సెం.మీ.
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యము = 2 (lb+ bh + lh)
= 2(64 × 1 + 1 × 1 + 1 × 64)
= 2 (64 + 1 + 64) = 2 × 129 = 258 చ.యూ.

2. l = 32 సెం.మీ., b = 2 సెం.మీ., h = 1 సెం.మీ.
A = 2 (lb + bh + lh)
= 2 (32 × 2 + 2 × 1 + 32 × 1)
= 2 (64 + 2 + 32)
= 2 × 98 = 196 చ.యూ.

3. l = 16 సెం.మీ., b = 4 సెం.మీ., h = 1 సెం.మీ.
A = 2(lb+ bh + lh)
= 2(16 × 4 + 4 × 1 + 16 × 1)
= 2 (64 + 4 + 16)
= 2 × 84 = 168 చ.యూ.

ప్రయత్నించండి

1. (i) సమ ఘనము ‘A’ యొక్క సంపూర్ణతల వైశాల్యం మరియు ‘B’ యొక్క ప్రక్కతల వైశాల్యము కనుగొనండి. (పేజీ నెం. 300)

సాధన.
a = 10 సెం.మీ.
పటం A యొక్క సంపూర్ణతల వైశాల్యము = 6a²
= 6 × (10)²
= 6 × 100 = 600 చ.సెం.మీ.
పటం B యొక్క ప్రక్కతల వైశాల్యము = 4a²
= 4 × (8)² [∵ a = 8 సెం.మీ. ]
= 4 × 64 = 256 చ.సెం.మీ.

(ii) ‘b’ భుజముగా గల రెండు సమఘనములు పటములో చూపిన విధముగా జతచేయబడి దీర్ఘఘనమును ఏర్పరిస్తే, ఆ దీర్ఘఘనము యొక్క సంపూర్ణతల వైశాల్యము ఎంత ?

సాధన.
ప్రక్క దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)

= 2(2b × b + b × b + 2b × b)
= 2(2b² + b² + 2b²)
= 2(5b²) = 10b² చ.యూ.

(iii) సమాన భుజము పొడవు గల 12 సమఘనములు ఏ విధముగా జతచేయడము వలన అత్యల్ప సంపూర్ణతల వైశాల్యము కలిగిన దీర్ఘ ఘనము ఏర్పడుతుందో వివరింపుము.

సాధన.
12 సమఘనాలను ఒకదాని ప్రక్క ఒకటి లేదా ఒకదానిపై ఒకటి అమర్చుట ద్వారా అత్యల్ప సంపూర్ణతల వైశాల్యం సంభవించదు.

∴ A = 2(lb + bh + lh)
= 2(12 × 1 + 1 × 1 + 12 × 1)
= 2(12 + 1 + 12)
= 2 × 25 = 50 చ.యూ
కానీ, 3 సమఘనాలపై నాలుగు వరుసలుగా అమర్చుట ద్వారా అత్యల్ప సంపూర్ణతల వైశాల్యం పొందవచ్చు.
∴ A = 2(lb+ bh + lh)
= 2(3 × 1 + 1 × 4 + 3 × 4) (∵ l = 3; b = 1; h = 4)
= 2(3 + 4 + 12) = 2 × 19 = 38 చ.యూ.

(iv) 4 × 4 × 4 కొలతలు గల ఒక సమఘనము రంగు వేయబడినది. ఆ ఘనము 64 సమఘనములుగా విభజింప బడినది. అయితే
(a) ఒక ముఖము మాత్రమే రంగు వేయబడినది. ఘనములు ఎన్ని ?
(b) రెండు ముఖములు రంగు వేయబడిన ఘనములు ఎన్ని ?
(c) మూడు ముఖములు రంగు వేయబడిన ఘనములు ఎన్ని ?
(d) ఏ ముఖము కూడ రంగు వేయబడని ఘనములు ఎన్ని ?
సాధన.
4 × 4 × 4 సమఘనం 64 సమఘనాలుగా విభజింపబడిన ఒక్కొక్క
సమఘనం యొక్క భుజం పొడవు = 1 యూ.

[∵ \(\frac{4 \times 4 \times 4}{64}\) = 1]
(a) ఒక ముఖము మాత్రమే రంగు వేయబడిన (a = 4) సమఘనాల సంఖ్య = 6(a – 2)² = 6(4 – 2)² = 6 × 4 = 24
(b) రెండు ముఖాలు రంగు వేయబడిన సమఘనాల సంఖ్య = 12(a – 2) = 12(4 – 2) = 24
(c) మూడు ముఖాలు రంగు వేయబడిన సమఘనాల సంఖ్య 4 × a = 4 × 2 = 8
(d) ఏ ముఖం కూడా రంగు వేయబడని సమఘనాల సంఖ్య = (a – 2)³ = (4 – 2)³ = (2)³ = 8

ఆలోచించి, చర్చించి వ్రాయండి

1. దీర్ఘఘనం సంపూర్ణతల వైశాల్యము = ప్రకృతల వైశాల్యము + 2 × భూవైశాల్యము అని మీరు చెప్పగలరా ? (పేజీ నెం. 299)

సాధన.
దీర్ఘఘనం సంపూర్ణతల వైశాల్యం = ప్రక్కతల వైశాల్యం + 2 × భూవైశాల్యం
= 2h(l + b) + 2 × lb
= 2lh +2bh +2lb
= 2(lb + bh + lh)
∴ దీర్ఘఘనం సంపూర్ణతల వైశాల్యం = ప్రక్కతల వైశాల్యం + 2 × భూవైశాల్యం అని చెప్పగలం.

2. పటము (i)లో చూపిన దీర్ఘఘనము భంగిమను పటము (ii)లో లాగ మార్చిన వాటి ప్రక్కతల వైశాల్యాలు సమానంగా ఉంటాయా ?
సాధన.
దీర్ఘఘనం యొక్క భంగిమను ఏ విధంగా మార్చినా దాని ప్రక్కతల వైశాల్యములు సమానంగా ఉండవు.

3. పొడవు (i), వెడల్పు (b), ఎత్తు (h) ల కొలతలు సమానముగా గల దీర్ఘఘనపు పటమును గీచి దాని ప్రక్కతల వైశాల్యము మరియు సంపూర్ణతల వైశాల్యములకు సూత్రము రాబట్టుము.
సాధన.
దీర్ఘఘనం యొక్క ప్రక్కతల వైశాల్యం

= 4 × ప్రక్కతల వైశాల్యము
= 2 (l × h) + 2 × (b × h) (1 + 2 + 3 + 4 తలాలు)
= 2h (l + b) చ.యూ. (1 = 3, 4 = 2)
దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 4 × ప్రక్కతల వైశాల్యం + పైన, క్రింది తలాల వైశాల్యం
= 2h (l + b) + 2(lb)
= 2lh + 2bh + 2lb
= 2(lb + bh + lh) చ.యూ.

AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Ex 14.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Exercise 14.2

ప్రశ్న 1.
ఈ క్రింది కొలతలు కలిగిన దీర్ఘఘనము యొక్క ఘనపరిమాణమును కనుగొనుము.

సాధన.

ప్రశ్న 2.
ఈ క్రింది కొలతలు కలిగిన బ్యాంకు యొక్క సామర్థ్యమును ఘనపు మీటర్లు మరియు లీటర్లలో కనుగొనుము.

సాధన.

ప్రశ్న 3.
ఒక సమఘనము యొక్క భుజమును సగము చేస్తే దాని ఘనపరిమాణము తగ్గుతుందా ? మారినచో ఎంత తగ్గును?
సాధన.
సమఘనం యొక్క భుజం (s) = a యూ. అనుకొనుము సమఘనం యొక్క ఘన పరిమాణం
(V₁) = (s)³ = a × a × a = a³
భుజాన్ని సగం చేయగా, 5 – 2
∴ సమఘనం యొక్క ఘనపరిమాణం
V₂ = (s)³ = (\(\frac {a}{2}\))³ = \(\frac {a³}{8}\)
V₂ = \(\frac {V}{8}\) లీక V₁ = 8V₂
∴ సమఘనం యొక్క ముజాన్ని సగం చేయగా దాని ఘనపరిమాణం ఆసలు ఘనపరిమాణంలో \(\frac {1}{8}\) వ వంతు తగ్గును.

ప్రశ్న 4.
ఈ క్రింది కొలతలు భుజంగా కలిగిన సమఘనముల యొక్క ఘనపరిమాణము కనుక్కోండి.
(i) 6.4 సెం.మీ. (ii) 1.3 మీ. (iii) 1.6 మీ.
సాధన.
సమఘన ఘనపరిమాణం (V) = a³

ప్రశ్న 5.
8 మీ. × 22.5 సెం.మీ. × 6 మీ. కొలతలుగా గల ఒక గోడను నిర్మించుటకు 25 సెం.మీ. × 11.25 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల ఇటుకలెన్ని అవసరము?
సాధన.
8 మీ. × 22.5 సెం.మీ. × 6 మీ కొలతలు గల గోడ ఘనపరిమాణం (V₁) = l₁ b₁ h₁
= 8మీ × 22.5 సెం.మీ. × 6 మీ
= 800 × 22.5 × 600 సెం.మీ.
25 సెం.మీ. × 11.25 సెం.మీ. × 6 సెం.మీ.లు కొలతలుగా గల ఇటుక ఘనపరిమాణం (V₂) = l₂ b₂ h₂
= 25 × 11.25 × 6
∴ కావలసిన ఇటుకల సంఖ్య
= \(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}=\frac{800^{32} \times 22.5^{2} \times 600^{100}}{25_{1} \times 11.25_{1} \times 6_{1}}\)
= 32 × 2 × 100 = 6400

ప్రశ్న 6.
25 సెం.మీ. పొడవు, 16 సెం.మీ. వెడల్పు మరియు 8 సెం.మీ. ఎత్తు కొలతలుగా గల దీర్ఘమన ఘనపరిమాణము, ప్రతీ భుజము 16 సెం.మీ.గా గల సమఘనము ఘనపరిమాణముతో ఎంత తేడా కలదు?
సాధన.
l = 25 సెం.మీ., b = 15 సెం.మీ., h = 8 సెం.మీ.
∴ దీర్ఘఘనం యొక్క ఘనపరిమాణం (V₁) = lbh
⇒ V₁ = 25 × 15 × 8 = 3000 సెం.మీ.
సమఘనం యొక్క ఘనపరిమాణం (V₂) = s³
⇒ V₂ = (16)³ = 16 × 16 × 16 = 4096 ఘ. సెం.మీ.
∴ V₂ – V₁ = 4096 – 3000 = 1096 ఘ. సెం.మీ.
∴ సమఘనం, దీర్ఘఘనాల పరిమాణాల మధ్య తేడా 1096 ఘ. సెం.మీ. ఉండును.

ప్రశ్న 7.
1సెం.మీ. మందము కలిగిన చెక్కతో 5 సెం.మీ. × 4 సెం.మీ. × 7 సెం.మీ. కొలతలు కలిగిన మూతగల పెట్టెను తయారుచేయడానికి ఎంత ఘనపరిమాణము గల చెక్క అవసరము?
సాధన.
బయటి కొలతలు 5 సెం.మీ. × 4 సెం.మీ × 7 సెం.మీ
గల చెక్క పెట్టి ఘనపరిమాణం V₁ = l × b × h
V₁ = 5 × 4 × 7
V₁ = 140 ఘ. సెం.మీ
లోపలి కొలతలు = l – 2w, b – 2w, h – 2w
= (5 – 2 × 1), (4 – 2 × 1), (7 – 2 × 1)
= (5 – 2), (4 – 2), (7 – 2)
= 3 సెం.మీ., 2 సెం.మీ., 5 సెం.మీ.
∴ 3 సెం.మీ., 2 సెం.మీ., 5 సెం.మీ.లతో ఏర్పడు చెక్క పెట్టె ఘనపరిమాణం
(V₂) = (l – 2w) (b – 2w) (h – 2w)
= 3 × 2 × 5
= 30 ఘ, సెం.మీ.
∴ కావలసిన చెక్క పెట్టి తయారుచేయుటకు అవసరమగు చెక్క ఘనపరిమాణం
= V₁ – V₂ = 140 – 30 = 110 ఘ. సెం.మీ.

ప్రశ్న 8.
20 సెం.మీ. × 18 సెం.మీ. × 16 సెం.మీ. కొలతలుగా గల దీర్ఘఘనం నుండి 4 సెం.మీ. భుజంగా గల ఎన్ని సమఘనములను ఏర్పరచవచ్చు?
సాధన.
20 సెం.మీ. × 18 సెం.మీ. × 16 సెం.మీ.
కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం . V₁ = lbh
∴ V₁ = 20 × 18 × 16
4 సెం.మీ. భుజంగా గల సమఘన ఘనపరిమాణం
⇒ V₂ = (s)³ = 4 × 4 × 4
∴ కావలసిన సమఘనాల సంఖ్య
= \(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}=\frac{26^{5} \times 18 \times 16}{A \times A \times A}\) = 90

ప్రశ్న 9.
12 సెం.మీ. × 9 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల దీర్ఘఘనం నుండి 4 సెం.మీ. × 3 సెం.మీ. × 2 సెం.మీ. కొలతలుగా గల దీర్ఘఘనాలను ఎన్నింటిని తయారుచేయవచ్చు?
సాధన.
12 సెం.మీ. × 9 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం
V₁ = l₁ × b₁ × h₁ = 12 × 9 × 6
4 సెం.మీ. × 3 సెం.మీ. × 2 సెం.మీ. కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం
V₂ = l₂ × b₂ × h₂ = 4 × 3 × 2
∴ కావలసిన సమఘనాల సంఖ్య
= \(\frac{V_{1}}{V_{2}}=\frac{12^{3} \times 9 \times 6}{A_{1} \times \beta^{\prime} \times 2}\) = 27

ప్రశ్న 10.
దీర్ఘఘనాకృతిలో ఉన్న ఒక పాత్ర 30 సెం.మీ. పొడవు, 25 సెం.మీ. వెడల్పు కలిగియున్నది. దానిలో 4.5 లీటర్ల నీటిని నింపుటకు ఎంత ఎత్తును కలిగి ఉండాలి?
సాధన.
దీర్ఘఘనాకార పాత్ర పొడవు (l) = 30 సెం.మీ.
వెడల్పు (b) = 25 సెం.మీ.
ఎత్తు (h) = ?
దీర్ఘఘనాకార పాత్రలో నీటి పరిమాణం (ఘనపరిమాణం) = 4.5 లీటర్లు
= 4.5 x 1000 ఘ. సెం.మీ.
= 4500 ఘ. సెం.మీ.
∴ l × b × h = 45000
⇒ 30 × 25 × h = 4500
⇒ h = \(\frac {4500}{30 × 25}\)
∴ h = 6 సెం.మీ

SCERT AP 10th Class Maths Textbook Solutions Chapter 1 పూర్ణ సంఖ్యలు Ex 1.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు Exercise 1.1

ప్రశ్న1.
యూక్లిడ్ భాగహార శేష విధి ఆధారంగా క్రింది జతల గ.సా.భాను కనుగొనండి.

(i) 900 మరియు 270
సాధన:
a = 900, b = 270 వీటిని .
a = bq + r రూపంలో వ్రాయగా
900 = 270(3) + 90;
270 = 90(3) + 0
కావున 900, 270ల గ.సా.భా = 90

రెండవ పద్ధతి :

∴ గ.సా.భా = 90.

(ii) 196 మరియు 38220
సాధన:
a = 38220; b = 196 అనుకొనుము
a = bq + r రూపంలో వ్రాయగా,
38220 = 196(195) + 0
కావున (∴ శేషం = 0) 196, 38220 ల గ.సా.భా = 196.

రెండవ పద్ధతి:

∴ 196, 38220 ల గ.సా.భా = 196

(iii) 1651 మరియు 2032
సాధన:
1651 మరియు 2032 ల గ.సా.భా
a = 2032, మరియు b = 1651 వీటిని
a = bq + r రూపంలో, వ్రాయగా
2032 = 1651(1) + 381
1651 = 381(4) + 127
381 = 127(3) + 0
∴ 1651 మరియు 2032 ల గ.సా.భా = 127

రెండవ పద్ధతి :

∴ 1651, 2032 ల గ.సా.భా = 127

ప్రశ్న2.
q ఏదైనా ఒక పూర్ణ సంఖ్య అయినప్పుడు ప్రతి ధన బేసి పూర్ణ సంఖ్య 6q+ 1 లేదా 6q + 3 లేదా 6q+ 5 రూపంలో ఉంటుందని చూపుము.
సాధన:
a ఏదైనా ఒక ధన బేసి పూర్ణ సంఖ్య అనుకుందాం. భాగాహార శేష విధిని a మరియు b = 6 పై అనువర్తింపగా 0 ≤ r < 6, కావున శేషం 0 లేదా 1 లేదా 2 లేదా 3 లేదా 4 లేదా 5 అగును. వీటి ఆధారంగా ణ విలువలు వరుసగా
a = 6q + 0 లేదా
= 6q + 1 లేదా
= 6q + 2 లేదా
= 6q + 3 లేదా
= 6q + 4 లేదా
= 6q + 5 అగును.
పై వాటిలో a = 6q+ 0, a = 6q + 2, a = 6q + 4 లు 2 చే నిశ్శేషంగా భాగింపబడును. కావున అవి సరి సంఖ్యలు.
కాగా మిగిలినవి a = 6q + 1
a = 6q+ 3
a = 6q + 5 లు 2 చే నిశ్శేషంగా భాగింపబడవు. కావున అవి సరిసంఖ్యలు కాలేవు. అందుచే అవి ఖచ్చితంగా ధన బేసి పూర్ణసంఖ్యలు అవుతాయి.

ప్రశ్న3.
ఏదైనా ధన పూర్ణసంఖ్య యొక్క వర్గం 3p లేదా 3p + 1 రూపంలో ఉంటుందని యూక్లిడ్ భాగహార శేష విధి ఆధారంగా చూపుము.
సాధన:
‘a’ అనునది ఏదైనా ధన పూర్ణ సంఖ్య అనుకొనుము. మరియు b = 3 అనుకుందాం.
యూక్లిడ్ భాగహార శేష న్యాయం ప్రకారం a = bq + r ఇచ్చట b = 3 కావున r = 0 లేదా 1 లేదా 2 అగును.
∴ a = 3q + 0 లేదా a = 3q + 1 లేదా a = 3q + 2
∴ a = 3q అయిన a2 = 9q2 = 3(3q7)
= 32 రూపం a = 3q + 1 అయిన
a² = (3q + 1)² = 9q² + 6q + 1
= 3[3q² + 2q] + 1
= 3p+ 1 రూపం
a = 3q + 2 అయిన a²
= (3q + 2)²
= 9q² + 12q + 4
= 3[3q² + 4q + 1] + 1
= 3p + 1 రూపం
కావున ఒక ధన పూర్ణ సంఖ్య యొక్క వర్గం 3p లేదా 3p+ 1 రూపంలో ఉండును.

ప్రశ్న4.
ఏదైనా ధన పూర్ణ సంఖ్య యొక్క ఘనం 9m లేదా 9m + 1 లేదా 9m + 8 రూపంలో ఉంటుందని చూపుము.
సాధన:
‘a’ అనునది ఏదేని ఒక ధన పూర్ణసంఖ్య మరియు b = 3.అనుకుందాం.
యూక్లిడ్ భాగహార శేష న్యాయం ప్రకారం
a = 3q + r ………… (1)
ఇక్కడ q 6 W మరియు 0 ≤ r < 2 అనగా r = 0 లేదా r = 1 లేదా r = 2

సందర్భం : 1
r = 0
(1) ⇒ a = 34
a³ = (3q)³
= 27q³
= 9 (3q³) = 9 m
ఇక్కడ m = 3q³.

సందర్భం : 2, r = 1
(1) ⇒ a = 3q + 1
a³ = (3q + 1)³
= 27q³ + 27q² + 9q + 1
= 9(3q³ + 3q² + q) + 1
= 9 m + 1 ఇక్కడ m = 3q³ + 3q² + q

సందర్భం : 3
r = 2 (1) = a = (3q + 2)3
= 27q3 + 54q2 + 36q+ 8 = 9(3q3 + 6q2 + 44) + 8
= 9m + 8 ఇక్కడ m= 3q + 6q2 + 4q .. కావున ధన పూర్ణసంఖ్య యొక్క ఘనము 9m లేదా 9m + 1 లేదా 9m + 8 రూపంలో ఉంటుంది.

రెండవ పద్ధతి :
a అనునది ఏదేని ధనపూర్ణ సంఖ్య మరియు b = 3 అనుకొనుము.
యూక్లిడ్ భాగహార శేష న్యాయం ప్రకారం.
a = 3q + r, q ∈ W, 0 ≤ r < 3
⇒ a³ = (3q + r)³
⇒ a³ = 27q² + 27q²r + 9qr² + r ………… (1)

సందర్భం : 1, r = 0
(1) ⇒ a³ = 27q³ = 9(3q³) = 9m
ఇక్కడ m = 3q³

సందర్భం : 2,
r = 1
(1) ⇒ a³ = 27q³ + 27q² + 9q + 1
= 9(3q³ + 3q² + 4) + 1
a3 = 9m + 1 ఇక్కడ m = 3q³ + 3q² + q

సందర్భం : 3,
r = 2
(1) ⇒ a³ = 27q³ + 54q² + 36q + 8
= 9(3q³ + 6q² + 4q) + 8
a³ = 9m + 8
ఇక్కడ m = 3q³ + 6q² + 4q
కావున ధనపూర్ణ సంఖ్య యొక్క ఘనం 9m లేదా 9m + 1 లేదా 9m + 8 రూపంలో ఉంటుంది.

ప్రశ్న5.
ఏదైన ధన పూర్ణ సంఖ్య n కు n, n + 2 లేదా n + 4 లలో ఏదైనా ఒకటి మాత్రమే 3 చే భాగింపబడుతుందని చూపుము.

(లేదా)

a ధన పూర్ణ సంఖ్య అయిన a, a + 2 మరియు a + 4 లలొ ఏదో ఒకటి మాత్రమే 3 చే భాగింపబడుతుందని చూపుము.
సాధన.
n ఏదేని ధనపూర్ణ సంఖ్య మరియు n ను 3 చే భాగించగా భాగఫలం q, శేషం / అనుకుందాం.
యూక్లిడ్ భాగహార శేషన్యాయం ప్రకారం. n = 3q + r – (1), 0 ≤ r  < 3, r = 0 లేదా 1 లేదా 2

పై మూడు సందర్భాల నుండి ఏదేని ధనపూర్ణ సంఖ్య n కు n n + 2 లేదా n + 4 లలో ఏదైనా ఒకటి మాత్రమే 3చే భాగింపబడుతుంది.

AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము) Ex 14.11 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Exercise 14.1

ప్రశ్న 1.
పటములో చూపిన విధముగా రెండు దీర్ఘఘనాకృతి పెట్టెలు ఇవ్వబడ్డాయి. ఏ పెట్టెను తయారు చేయడానికి తక్కువ పరిమాణపు సామాగ్రి అవసరమవుతుంది?

సాధన.
దీర్ఘఘనం యొక్క ఘనపరిమాణం
(V₁) = lbh
= 60 × 40 × 50
V₁ = 1,20,000 ష్మణమూ.
సమఘనం యొక్క ఘనపరిమాణం
V₂ = (a)³
= (50)³ = 50 × 50 × 50
V₂ = 1,25,000 ఘ.యూ.
∴ V₁ < V₂
∴ మొదటి దీర్ఘఘనాన్ని తయారుచేయుటకు తక్కువ పరిమాణపు సామాగ్రి అవసరం.

ప్రశ్న 2.
600 చ.సెం.మీ. సంపూర్ణతల వైశాల్యం గల సమఘనం యొక్క భుజం పొడవును కనుక్కోండి..
సాధన.
సమఘనం యొక్క సంపూర్ణతల వైశాల్యం = 6a²
⇒ 6a² = 600
a² = \(\frac {600}{6}\) = 100
a² = 100
a = \(\sqrt{100}\) = 10
∴ సమఘనం యొక్క భుజం (a) = 10 సెం.మీ.

ప్రశ్న 3.
ప్రమీల 1 మీ. × 2 మీ. × 1.5 మీ. కొలతలు గల ఒక పెట్టెకు రంగు వేసింది. పెట్టె యొక్క పై ముఖము, అడుగు ముఖమును మినహాయించి మిగిలిన ముఖముల వైశాల్యముల మొత్తము ఎంత ?
సాధన.
దీర్ఘఘనము యొక్క పై మరియు అడుగు ముఖాలు కాకుండా మిగిలిన ముఖాల యొక్క మొత్తం వైశాల్యం దాని ప్రక్కతల వైశాల్యానికి సమానం అవుతుంది.
l = 1 మీ., b = 2 మీ., h = 1.5 మీ.
A= 2h (l + b)
= 2 × 1.5 (1 + 2)
= 3 × 3 = 9 ఘ.మీ.

ప్రశ్న 4.
20 సెం.మీ. × 15 సెం.మీ. × 12 సెం.మీ కొలతలుగా గల దీర్ఘఘనమునకు రంగు వేయుటకు చదరపు సెంటీ మీటరునకు 5 పైసలు చొప్పున ఎంత ఖర్చు అగును?
సాధన.
l = 20 సెం.మీ., b + 15 సెం.మీ., h = 12 సెం.మీ.
∴ దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం
A = 2(lb+ bh + lh)
= 2(20 × 15 + 15 × 12+ 20 × 12)
= 2(300 + 180 + 240)
= 2 × 720
= 1440 చ, సెం.మీ.
1 సెం.మీ.నకు 5 పైసలు వంతున 1440 చ సెం.మీ,
దీర్ఘఘనానికి రంగు వేయుటకు అగు ఖర్చు
= 1440 × 5 పై
= 7200 పై
= రూ. = \(\frac {7200}{100}\) = రూ. 72

AP SCERT 8th Class Maths Textbook Solutions Chapter 13 త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట InText Questions

ఇవి చేయండి

1. త్రిమితీయాలు గల కొన్ని వస్తువుల పేర్లు వ్రాయండి. (పేజీ నెం. 282)
సాధన.
1. సమఘనం
2. స్థూపం
3. గోళం
4. దీర్ఘ ఘనం
5. శంఖువు

2. ద్విమితీయ ఆకారాలు గల కొన్ని పటముల పేర్లు వ్రాయండి. (పేజీ నెం. 282)
సాధన.
1. చతురస్రం
2. దీర్ఘచతురస్రం
3. రేఖాఖండం
4. వృత్తం
5. త్రిభుజము

3. గాలిపటము (kite) చిత్రము గీయండి. అది ద్విమితీయ పటమా లేక త్రిమితీయ వస్తువా గుర్తించండి. (పేజీ నెం. 282)
సాధన.

ఇది ఒక ద్విమితీయ పటం

4. ఘనము, దీర్ఘఘనాకారము గల కొన్ని వస్తువులను గుర్తించండి. (పేజీ నెం. 282)
సాధన.

5. వృత్తము, గోళము మధ్య తేడా ఏమిటి ?
సాధన.
వృత్తం – ఇది ఒక ద్విమితీయ ఆకారం ; గోళం – ఇది ఒక త్రిమితీయ వస్తువు.

6. కింద ఇచ్చిన పట్టకముల పేర్లు రాయంది. (పేజీ నెం. 290)

సాధన.
(i) సమఘనం
(ii) త్రిభుజాకార పట్టకం
(iii) పంచభుజాకార పట్టకం
(iv) షడ్భుజాకార పట్టకం దీర్ఘచతురస్రాకార పట్టకం

7. కింద ఇచ్చిన పిరమిడ్ ల పేర్లను రాయండి. (పేజీ నెం. 290)

సాధన.
(i) చతురస్రాకార పిరమిడ్
(ii) పంచభుజాకార పిరమిడ్
(iii) షడ్భుజాకార పిరమిడ్

8. కింది పట్టిక నందు వాటి భుజముల ఆధారంగా పిరమిడ్ పట్టకము యొక్క పేర్లను వ్రాయండి. (పేజీ నెం. 290)

సాధన.

9. పట్టకము, పిరమిడ్ల మధ్య తేడాలను వివరించండి. (పేజీ నెం. 290)
సాధన
పట్టకంలో పై, కింది తలాల యొక్క భుజాల సంఖ్య సమానంగా ఉంటుంది.
పిరమిడ్ లో భూమి సమతలంగా ఉండి ఆ సమతలాల శీర్షాలతో ఏర్పడు అంచులన్నీ పైన ఒకే బిందువు వద్ద ఏకీభవిస్తాయి.

ప్రయత్నించండి

1. బహుముఖి ఫలకముగా గల వస్తువులకు 3 ఉదాహరణలు ఇవ్వండి. (పేజీ నెం. 287)
సాధన.
బహుముఖ ఫలకముగా గల వస్తువులు :

2. బహుముఖేతర ఫలకముగా గల వస్తువులకు 3 ఉదాహరణలు ఇవ్వండి. (పేజీ నెం. 282)
సాధన.
బహుముఖేతర ఫలకాలు గల వస్తువులు :

ఆలోచించి, చర్చించి వ్రాయండి

1. ఒక వస్తువు వివిధ స్థానాల నుండి వివిధ ఆకారాలలో కనిపిస్తుంది. ఉదాహరణకు

పై పటమును పై నుండి చూసినప్పుడు, కింది నుండి చూసినప్పుడు కనిపించు ఆకారము యొక్క చుట్టుకొలత, వైశాల్యము కనుక్కోండి. (పేజీ నెం. 283)
సాధన.
ఒక్కొక్క తలం యొక్క భుజం ‘1’ యూనిట్ అనుకొనిన
వివిధ స్థానాలలోని ఆకారాలు (I)
1. ముందు నుండి చూసినపుడు
2. పై నుండి చూసినప్పుడు
3. కింద నుండి చూసినప్పుడు

వాటి వైశాల్యాలు (II)
A = (1 × 1) + (1 × 1) + (1 × 1) = 3 చ.యూ.
A= (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 చ.యూ.
A = (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 చ.యూ.

చుట్టుకొలతలు (III)
1. —————–> 1 + 1 + 1 = 3 యూనిట్లు
2. ————–> 2(l + b) = 2 (3 + 2) = 2 × 5 = 10 యూనిట్లు
3. ————–> 2(l + b) = 2 (3 + 2) = 2 × 5 = 10 యూనిట్లు

2. ఒక క్రమ పిరమిడ్ నందు అడుగు తలము యొక్క భుజముల సంఖ్య అనంతముగా పెంచినచో, ఆ పిరమిడ్ మార్పు చెందు ఆకారమును గమనించండి. (పేజీ నెం. 291)
సాధన.
ఒక క్రమ పిరమిడ్ నందు అడుగు తలము యొక్క భుజాల సంఖ్యను అనంతంగా పెంచినచో ఆ తలం ఒక వృత్తాకారాన్ని సంతరించుకుంటుంది. తద్వారా ఆ పిరమిడ్ ఒక శంఖువు ఆకారాన్ని ఆపాదించుకుంటుంది,

AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.3

ప్రశ్న 1.
క్రింది ద్విపదులను గుణించండి.
(i) 2a – 9 మరియు 3a + 4
(ii) x – 2y మరియు 2x – y
(iii) kl + lm మరియు k – l
(iv) m² – n² మరియు m + n
సాధన.
(i) 2a – 9 మరియు 3a + 4
(2a – 9) (3a + 4) = 2a (3a + 4) – 9(3a + 4)
= 6a² + 8a – 27a – 36
= 6a² – 19a – 36

(ii) x – 2y మరియు 2x – y
(x – 2y) × (2x – y) = x(2x – y) – 2y(2x – y)
= 2x² – xy – 4xy + 2y²
= 2x² – 5xy + 2y²

(iii) kl + lm మరియు k – l
(kl + lm) (k – l) = kl(k – l) + lm (k – l).
= k²l – l²k + klm – l²m

(iv) m² – n² మరియు m + n
(m² – n²) (m + n) = m²(m + n) – n²(m + n)
= m³ + m²n – n²m – n³

2. క్రింది లబ్ధాలను కనుగొనండి.

ప్రశ్న (i)
(x + y) (2x – 5y + 3xy)
సాధన.
= x (2x – 5y + 3xy) + y(2x – 5y + 3xy)
= 2x² – 5xy + 3x²y + 2xy – 5y² + 3xy²
= 2x² – 5y² – 2xy + 3x²y + 3xy²

ప్రశ్న (ii)
(a – 2b + 3c) (ab² – a²b)
సాధన.
= a (ab² – a²b) – 2b (ab² – a²b) + 3c (ab² – a²b)
= a²b² – a³b – 2ab³ + 2a²b² + 3cab² – 3ca²b
= 3a²b² – a³b – 2ab³ + 3cab² – 3ca²b

ప్రశ్న (iii)
(mn – kl + km) (kl – lm)
సాధన.
= kl (mn – kl + km) – lm (mn – kl + km)
= klmn – k²l² + k²lm – lm²n + kl²m – klm²

ప్రశ్న (iv)
(p³ + q³)(p – 5q + 6r)
సాధన.
= p³ (p – 5q + 6r) + q³ (p – 5q + 6r)
= p⁴ – 5p³q + 6p³r + pq³ – 5q⁴ + 6rq³
= p⁴ – 5q⁴ – 5p³q + 6p³r + pq³ + 6rq³

3. సూక్ష్మీకరించండి.

ప్రశ్న (i)
(x – 2y) (y – 3x) + (x + y) (x – 3y) – (y – 3x) (4x – 5y)
సాధన.
= (y – 3x) [x – 2y – (4x – 5y)] + (x + y) (x – 3y)
= (y – 3x) [x – 2y – 4x + 5y] + (x + y) (x – 3y)
= (y – 3x) (3y – 3x) + (x + y) (x – 3y)
= y (3y – 3x) – 3x (3y – 3x) + x (x – 3y) + y (x – 3y)
= 3y² – 3xy – 9xy + 9x² + x² – 3xy + xy – 3y²
= 10x² – 14xy

ప్రశ్న (ii)
(m + n) (m² – mn + n²)
సాధన.
= m (m² – mn + n²) + n (m² – mn + n²)
= m³ – m²n + n²m + nm² – mn² + n³
= m³ + n³

ప్రశ్న (iii)
(a – 2b + 5c) (a – b) – (a – b – c) (2a + 3c) + (6a + b) (2c – 3a – 5b)
సాధన.
= a(a – 2b + 5c) – b (a – 2b + 5c) – 2a (a – b – c) – 3c (a – b – c) + 6a (2c – 3a – 5b) + b (2c – 3a – 5b)
= a² – 2ab + 5ac – ab + 2b² – 5bc – 2a² + 2ab + 2ac – 3ac
+ 3bc + 3c² + 12ac – 18a² – 30ab + 2bc – 3ab – 5b²
= – 19a² – 3b² – 34ab + 16ac + 3c²

ప్రశ్న (iv)
(pq – qr + pr) (pq + qr) – (pr + pq) (p + q – r)
సాధన.
= pq (pq – qr + pr) + qr (pq – qr + pr) – pr (p + q – r)
= p²q² – pq²r + p²qr + pq²r – q²r² + pqr² – p²r – pqr + pr² – p²q – pq² + pqr
= p²q² – q²r² + p²qr + pqr² – p²r + pr² – p²q – pq²

ప్రశ్న 4.
a, b, cలు మూదు ధన వాస్తవసంఖ్యలు మరియు \(\frac{\mathbf{a}+\mathbf{b}-\mathbf{c}}{\mathbf{c}}=\frac{\mathbf{a}-\mathbf{b}+\mathbf{c}}{\mathbf{b}}=\frac{-\mathbf{a}+\mathbf{b}+\mathbf{c}}{\mathbf{a}}\), అయిన \(\frac{(\mathbf{a}+\mathbf{b})(\mathbf{b}+\mathbf{c})(\mathbf{c}+\mathbf{a})}{\mathbf{a b c}}\) విలువ కనుగొనుము
సాధన.

AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.2

ప్రశ్న 1.
పట్టికను పూర్తి చేయండి.

సాధన.

ప్రశ్న 2.
4y (3y + 4)ను సూక్ష్మీకరించంది.
సాధన.
4y (3y + 4) = 4y × 3y + 4y × 4
= 12y² + 16y

ప్రశ్న 3.
x (2x² – 7x + 3) ను సూక్ష్మీకరించి
(i) x = 1 మరియు (ii) x = 0 విలువలకు లబ్ధం విలువ కనుగొనండి.
సాధన.
x (2x² – 7x + 3)
= x × 2x² – x × 7x + x × 3
= 2x³ – 7x² + 3x

(i) x = 1 అయిన 2x³ – 7x² + 3x
= 2(1)³ – 7(1)² + 3(1)
= 2 – 7 + 3 = – 2

(ii) x = 0 అయిన 2x³ – 7x² + 3x
= 2(0)³ – 7(0)³ + 3(0) = 0

ప్రశ్న 4.
క్రింది లబాల మొత్తాన్ని కనుగొనండి.
a(a – b), b(b – c), c(c – a)
సాధన.
a (a – b) + b (b – c) + c (c – a)
= a × a – a × b + b × b – b × c + c × c – c × a
= a² – ab + b² – bc + c² – ca
= a² + b² + c² – ab – bc – ca

ప్రశ్న 5.
ఈ క్రింది లబ్దాల మొత్తాన్ని కనుగొనండి.
x(x + y – r), y(x – y + r), z(x – y – z)
సాధన.
x (x + y – r) + y (x – y + r) + z (x – y – z)
= x² + xy – xr + xy – y² + yr + zx – yz – z²
= x² – y² – z² + 2xy – xr + yr + zx – yz

ప్రశ్న 6.
3x(x + 2y) లబ్ధం నుండి 2x(5x – y) లబాన్ని తీసివేయండి.
సాధన.
3x (x + 2y) – 2x (5x – y)
= (3x × x + 3x × 2y) – (2x × 5x – 2x × y)
= 3x² + 6xy – (10x² – 2xy)
= 3x² + 6xy – 10x² + 2xy
= 8xy – 7x²

ప్రశ్న 7.
6k(2k + 3l – 2m) నుండి 3k(5k – l + 3m) ను తీసివేయండి.
సాధన.
6k (2k + 3l – 2m) – 3k (5k – l + 3m)
= 12k² + 18kl – 12km – 15k² + 3kl – 9km
= – 3k² + 21kl – 21km

ప్రశ్న 8.
a²(a – b + c) + b² (a + b – c) – c² (a – b – c)ని సూక్ష్మీకరించండి.
సాధన.
a²(a – b + c) + b²(a + b – c) – c² (a – b – c)
= a³ – a²b + a²c + ab² + b³ – cb² – c²a + c²b + c³
= a³ + b³ + c³ – a²b + ab² – cb² – c²a + c²b + a²c

AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.1

ప్రశ్న 1.
దిగువ ఇచ్చిన ఏకపది జతల లబ్దాన్ని కనుగొనండి.
(i) 6, 7k
(ii) – 3l, – 2m
(iii) – 5t², – 3t²
(iv) -5p², – 2p
సాధన.
(i) 6, 7k ల లబ్దం = 6 × 7k = 42k
(ii) – 3l, – 2m ల లబ్దం = (-3l) × (-2m) = 6lm
(iii) – 5t², – 3t² ల లబ్ధం = (-5t²) × (-3t²) = + 15t⁴
(iv) 6n, 3m ల లబ్దం = 6n × 3m = 18mn
(v) – 5p², – 2p ల లబ్ధం = (-5p²) × (-2p) = + 10p³

ప్రశ్న 2.
క్రింది లబ్ధాల పట్టికను పూర్తిచేయండి.

సాధన.

ప్రశ్న 3.
క్రింది పట్టికలో కొన్ని దీర్ఘఘనాల పొడవు, వెడల్పు మరియు ఎత్తుల కొలతలు ఇవ్వబడినవి. వాటి ఘనపరిమాణాన్ని కనుగొనండి.

సాధన.

ప్రశ్న 4.
క్రింది ఏకపదుల లబ్ధాన్ని కనుగొనండి.
(i) xy, x²y, xy, x
(ii) a, b, ab, a³b, ab³
(iii) kl, lm, km, klm
(iv) pq, pqr, r
(v) – 3a, 4ab, – 6c, d
సాధన.
(i) xy, x²y, xy, xల లబ్దం = xy × x²y × xy × x
= x⁵ × y³ = x⁵y³
(ii) a, b, ab, a³b, ab²ల లబ్దం = a × b × ab × a³b × ab³
= a⁶ × b⁶ = a⁶b⁶
(iii) kl, lm, km, klm = kl × lm × km × klmల లబ్దం = k³ × l³ × m³ = k³l³m³
(iv) pq, pqr, r = pq × pqr × rల లబ్దం = p² × q² × r² = p²q²r²
(v) – 3a, 4ab, -6c, dల లబ్దం = (-3a) × 4ab (-6c) × d
= + 72a² × b × c × d
= 72a²bcd

ప్రశ్న 5.
A = xy, B = yz wodi C = zx, అయన ABC = ………………….
సాధన.
ABC = xy × yz × zx = x²y²z²

ప్రశ్న 6.
P = 4x², T = 5x మరియు R = 5y, అయన \(\frac {PTR}{100}\) = ……………….
సాధన.
\(\frac{\mathrm{PTR}}{100}=\frac{4 \mathrm{x}^{2} \times 5 \mathrm{x} \times 5 \mathrm{y}}{100}=\frac{100 \mathrm{x}^{3} \mathrm{y}}{100}\) = x³y

ప్రశ్న 7.
స్వంతంగా కొన్ని ఏకపదులను వ్రాసి, వాటి లబ్దాన్ని కనుగొనండి.
సాధన.
కొన్ని ఏకపదుల లబ్ధం
(i) abc × a²bc = a³b²c²
(ii) xy × x²z × yz² = x³y²z²
(iii) p × q² × r³ = pq²r³