Mahesh

SCERT AP 8th Class Maths Solutions Chapter 4 ఘాతాంకాలు మరియు ఘాతాలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు InText Questions

ఇవి చేయండి

1. క్రింది వానిని సూక్ష్మీకరించండి. (పేజీ నెం. 81)
(i) 3⁷ × 3³
(ii) 4 × 4 × 4 × 4 × 4
(iii) 3⁴ × 4³
సాధన.
(i) 3⁷ × 3³ = 3⁷⁺³ = 3¹⁰ [∵ a^m × aⁿ = a^m+n)
(ii) 4 × 4 × 4 × 4 × 4 = 4⁵ [∵ a × a × a × ……. m సార్లు = a^m]
(iii) 3⁴ × 4³ = 81 × 64 = 5184

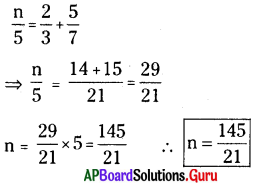
2. హైదరాబాద్ మరియు ఢిల్లీల మధ్య రైలు మార్గములో దూరము 1674.9 కి.మీ. దీనిని సెంటీమీటర్లలోకి మార్చి ఘాతాంక రూపంలో రాయండి. దీనిని శాస్త్రీయ రూపంలో కూడా రాయండి. (పేజీ నెం. 81)
సాధన.
హైదరాబాద్, ఢిల్లీల మధ్య దూరం
= 1674.9 కి. మీ. = 1674.9 × 1000 మీటర్లు = 1674900 మీ.
= 1674900 × 100 సెం.మీ. = 167490000 సెం.మీ.
= 167490000 సెం.మీ. = 16749 × 10⁴ సెం.మీ.

3. 10^-10 కు సమానమయ్యే విలువ ఎంత ? (పేజీ నెం. 83)
సాధన.
10^-10 = \(\frac{1}{10^{10}}\) [∵ \(a^{-n}=\frac{1}{a^{n}}\)]

4. క్రిందివాని గుణకార విలోమాలను కనుగొనుము. (పేజీ నెం. 83)
(i) 3^-5
(ii) 4^-3
(iii) 7^-4
(iv) 7^-3
(v) x^-n
(vi) \(\frac{1}{4^{3}}\)
(vii) \(\frac{1}{10^{3}}\)
సాధన.
(i) 3^-5 ⇒ 3^-5 × x = 1 ⇒ x = \(\frac{1}{3^{-5}}\) = 3⁵ [∵ 3^-5 × 3⁵ = 1]
(ii) 4^-3 ⇒ 4^-3 × x = 1 ⇒ x = \(\frac{1}{4^{-3}}\) = 4³
(iii) 7^-4 ⇒ 7^-4 × x = 1 ⇒ x = \(\frac{1}{7^{-4}}\) = 7⁴
(iv) 7^-3 ⇒ 7^-3 × x = 1 ⇒ x = \(\frac{1}{7^{-3}}\) = 7³
(v) x^-n ⇒ x^-n × k = 1 ⇒ k = \(\frac{1}{x^{-n}}\) = xⁿ
(vi) \(\frac{1}{4^{3}}\) ⇒ \(\frac{1}{4^{3}}\) × x = 1 ⇒ x = 4³
(vii) \(\frac{1}{10^{3}}\) ⇒ \(\frac{1}{10^{3}}\) × x = 1 ⇒ x = 10³

5. క్రింది సంఖ్యలను ఘాతాంకాలను ఉపయోగించి విస్తృత రూపంలో వ్రాయండి. (పేజీ నెం. 84)
(i) 543.67
సాధన.
543.67 = (5 × 100) + (4 × 10) + (3 × 10°) + \(\left(\frac{6}{10}\right)+\left(\frac{7}{10^{2}}\right)\)
= (5 × 10²) + (4 × 10) + (3 × 10°) + (6 × 10^-1) + (7 × 10^-2) [∵ aⁿ = a^-n]

(ii) 7054.243
సాధన.
7054.243 = (7 × 1000) + (0 × 100) + (5 × 10) + (4 × 10°) + \(\left(\frac{2}{10}\right)+\left(\frac{4}{100}\right)+\left(\frac{3}{1000}\right)\)
= (7 × 10³) + (0 × 10²) + (5 × 10¹) + (4 × 10°) + (2 × 10^-1) + (4 × 10^-2) + (3 × 10^-3)

(iii) 6540.305
సాధన.
6540.305 = (6 × 1000) + (5 × 100) + (4 × 10) + (0 × 10°) + \(\left(\frac{3}{10}\right)+\left(\frac{0}{100}\right)+\left(\frac{5}{1000}\right)\)
= (6 × 10³) + (5 × 10²) + (4 × 10¹) + (0 × 10°) + (3 × 10^-1) + (0 × 10^-2) + (5 × 10^-3)

(iv) 6523.450
సాధన.
6523.450 = (6 × 1000) + (5 × 100) + (2 × 10) + (3 × 10°) + \(\left(\frac{4}{10}\right)+\left(\frac{5}{100}\right)+\left(\frac{0}{1000}\right)\)
= (6 × 10³) + (5 × 10²) + (2 × 10¹) + (3 × 10°) + (4 × 10^-1) + (5 × 10^-2) + (0 × 10^-3)

6. క్రింది వానిని సూక్ష్మీకరించి ఒకే ఘాతాంకంగా వ్యక్తపరచుము. (పేజీ నెం. 85)
(i) 2^-3 × 2^-2
(ii) -7² × 7⁵
(iii) 3⁴ × 3^-5
(iv) 7⁵ × 7^-4 × 7^-6
(v) m⁵ × m^-10
(vi) (-5)^-3 × (-5)^-4
సాధన.

7. క్రింది వాక్యాలలోని సంఖ్యలను ప్రామాణిక రూపంలోనికి మార్చి వాక్యాలను తిరిగి వ్రాయండి. (పేజీ నెం. 93)
i) భూమి నుంచి సూర్యుని దూరం 149,600,000,000 మీ.
సాధన.
149,600,000,000 మీ. = 1496 × 10⁸ మీ.

ii) సూర్యుని సరాసరి వ్యాసార్ధం 695000 కి.మీ.
సాధన.
695000 కి.మీ. = 695 × 10³ కి.మీ.

iii) మనిషి తల వెంట్రుకల మందం 0.005 నుంచి 0.001 సెం.మీ. వరకు ఉంటుంది.
సాధన.
0.005 నుండి 0.001 సెం.మీ.
= \(\frac{5}{1000}\) నుండి \(\frac{1}{1000}\) సెం.మీ.
= 5 × 10^-3 నుండి 1 × 10^-3 సెం.మీ.

iv) ఎవరెస్టు శిఖరం యొక్క ఎత్తు 8848 మీ.
సాధన.
8848 మీ. యొక్క ప్రామాణిక రూపం = 8848 మీ.

8. ఈ క్రింది సంఖ్యలను ప్రామాణిక రూపంలో వ్రాయండి. (పేజీ నెం. 93)
(i) 0.0000456
(ii) 0.000000529
(iii) 0.0000000085
(iv) 6020000000
(v) 35400000000
(vi) 0.000437 × 10⁴
సాధన.
(i) 0.0000456 = \(\frac{456}{10000000}\) = 456 × 10^-7
(ii) 0.000000529 = \(\frac{529}{1000000000}\) = 529 × 10^-9
(iii) 0.0000000085 = \(\frac{85}{10000000000}\) = 85 × 10^-10
(iv) 6020000000 = 602 × 10000000 = 602 × 10⁷
(v) 35400000000 = 354 × 100000000 = 354 × 10⁸
(vi) 0.000437 × 10⁴ = \(\frac{437}{1000000}\) × 10⁴
= 437 × 10^-6 × 10⁴
= 437 × 10^{(-6 ) + 4}
= 437 × 10^-2

SCERT AP 8th Class Maths Solutions Chapter 4 ఘాతాంకాలు మరియు ఘాతాలు Ex 4.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు Exercise 4.2

1. క్రింది సంఖ్యలను ప్రామాణిక రూపంలో వ్యక్త పరచండి.
(i) 0.000000000947
సాధన.
= \(\frac{947}{1000000000000}\) = 947 × 10^-12

(ii) 543000000000
సాధన.
= 543 × 1000000000 = 543 × 10⁹

(iii) 48300000
సాధన.
= 483 × 100000 = 483 × 10⁵

(iv) 0.00009298
సాధన.
\(\frac{9298}{100000000}\) = 9298 × 10^-8

(v) 0.0000529
సాధన.
\(\frac{529}{10000000}\) = 529 × 10^-7

2. క్రింది సంఖ్యలను సాధారణ రూపంలో వ్యక్త పరచండి.
(i) 4.37 × 10⁵
సాధన.
= 4.37 × 100000 = 437000

(ii) 5.8 × 10⁷
సాధన.
= 5.8 × 10000000 = 58000000

(iii) 32.5 × 10^-4
సాధన.
= \(\frac{32.5}{10^{4}}=\frac{32.5}{10000}\) = 0.00325

(iv) 3.71529 × 10⁷
సాధన.
= 3.71529 × 10000000 = 37152900

(v) 3789 × 10^-5
సాధన.
= \(\frac{3789}{10^{5}}=\frac{3789}{100000}\) = 0.03789

(vi) 24.36 × 10^-3
సాధన.
\(\frac{24.36}{10^{3}}=\frac{24.36}{1000}\)
= 0.02436

3. క్రింది సమాచారంలోని సంఖ్యలను ప్రామాణిక రూపంలో వ్రాయండి.
(i) బాక్టీరియా పరిమాణము 0.0000004 మీ.
సాధన.
= \(\frac{4}{10000000}\) మీ. = 4 × 10^-7 మీ.

(ii) ఎర్రరక్త కణాల పరిమాణము 0.000007 మి.మీ.
సాధన.
= \(\frac{7}{1000000}\) = 7 × 10^-6 మి.మీ.

(iii) కాంతివేగము 300000000 మీ./సె.
సాధన.
= 3 × 10,00,00,000 = 3 × 10⁸ మీ./సె.

(iv) భూమికి, చంద్రునికి మధ్య దూరం 384467000 మీ. (సుమారుగా)
సాధన.
= 384467 × 1000 మీ.
= 384467 × 10³ మీ.

(v) ఎలక్ట్రాన్ ఆవేశం 0.0000000000000000016 కూలూంబులు.
సాధన.
= 0.0000000000000000016
= \(\frac{16}{10000000000000000000}\)
= \(\frac{16}{10^{19}}\)
= 16 × 10^-19 కూలూంబులు

(vi) పేపర్ యొక్క మందం 0.0016 సెం.మీ.
సాధన.
= 0.0016 సెం.మీ. = \(\frac{16}{10000}\)
= \(\frac{16}{10^{4}}\) = 16 × 10^-4 సెం.మీ.

(vii) కంప్యూటర్ చిప్ లోని తీగ వ్యాసం 0.000005 సెం.మీ.
సాధన.
= 0.000005 సెం.మీ. = \(\frac{5}{1000000}\) సెం.మీ.
= \(\frac{5}{10^{6}}\) = 5 × 10^-6 సెం.మీ.

4. ఒక పుస్తకాల కట్టలో 20 మి.మీ. మందం గల 5 పుస్తకాలు 0.016 మి.మీ, మందం గల 5 పేపర్లు కలవు. అయిన పుస్తకాల కట్ట యొక్క మొత్తం మందమును కనుగొనుము.
సాధన.
పుస్తకాల కట్ట యొక్క మొత్తం మందం = (5 పుస్తకాలు × పాటి మందం) + (5 పేపర్లు × వాటి మందం)
= (20 మి.మీ. × 5) + (0.016 మి.మీ. × 5)
= (100 మి.మీ. + 0.080 మి.మీ.)
= (100 + 0.08) మి.మీ.
= 100.08 మి.మీ.
= 1.0008 × 10² మి.మీ.

5. ఘాతాంకాలు కలిగిన కొన్ని సమస్యలను రాకేష్ క్రింది విధంగా సాధించాడు. నీవు రాకేష్ తో ఏకీభవిస్తావా ? నీ సమాధానమును సమర్థించుము.
(i) x^-3 × x^-2 = x^-6
సాధన.
⇒ x^{-3 + (-2)} = x^-6 [∵ am × an = am+n]
⇒ x^-5 = x^-6 ⇒ -5 ≠ -6
[∵ భూములు సమానం కావున ఘాతాంకాలు సమానాలు]
∴ ఈ సందర్భంలో రాకేష్ సమాధానంతో ఏకీభవించుట లేదు. ఎందుకనగా – 5 ≠ – 6 కావున.

(ii) \(\frac{x^{3}}{x^{2}}\) = x⁴
సాధన.
⇒ x^3-2 = x⁴ [∵ \(\frac{a^{m}}{a^{n}}=a^{m-n}\)]
⇒ x¹ = x⁴ ⇒ 1 ≠ 4
[∵ భూములు సమానం కావున ఘాతాంకాలు సమానాలు]
∴ ఈ సందర్భంలో రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

iii) (x²)³ = x²³ = x⁸
సాధన.
⇒ x^2×3= x^2×2×2 = x⁸ [∵ (a^m)ⁿ = a^mn)
⇒ x⁶ = x⁸ ⇒ 6 ≠ 8
∴ ఈ సందర్భంలో రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

iv) x^-2 = \(\sqrt{x}\)
సాధన.
⇒ x^-2 = x^1/2 [∵ \(\sqrt[n]{a}=a^{1 / n}\)]
⇒ -2 = \(\frac {1}{2}\)
∴ ఇది అసంభవం కావున ఈ సందర్భంలో కూడా రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

v) 3x^-1 = \(\frac{1}{3 x}\)
సాధన.
⇒ \(\frac{3}{x}=\frac{1}{3 x}\)
⇒ 3 × 3 = \(\frac{x}{x}\)
⇒ x⁰ = 9
⇒ 1 = 9
∴ ఇది అసంభవం కావున ఈ సందర్భంలో కూడా రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

SCERT AP 8th Class Maths Solutions Chapter 4 ఘాతాంకాలు మరియు ఘాతాలు Ex 4.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు Exercise 4.1

1. సూక్ష్మీకరించి తగు కారణాలు తెలుపుము.
(i) 4^-3
(ii) (-2)⁷
(iii) \(\left(\frac{3}{4}\right)^{-3}\)
(iv) (-3)^-4
సాధన.
(i) 4^-3 = \(\frac{1}{4^{3}}=\frac{1}{64}\)
[∵ \(a^{-n}=\frac{1}{a^{n}}\)]

(ii) (-2)⁷ = – (2)⁷ = – 128 [∵ 7 బేసిసంఖ్య]
ఎందుకనగా (-a)ⁿ విస్తరణలో n బేసిసంఖ్య అయిన (-a)ⁿ = – aⁿ అగును.

(iii) \(\left(\frac{3}{4}\right)^{-3}\)

(iv) (3)^-4 = \(\frac{1}{(-3)^{4}}\) [∵ \(a^{-n}=\frac{1}{a^{n}}\)]
= \(\frac{1}{3^{4}}\) [∵ 4 ఒక సరిసంఖ్య]
= \(\frac {1}{81}\)

2. కింది వానిని సూక్ష్మీకరింపుము.
(i) \(\left(\frac{1}{2}\right)^{4} \times\left(\frac{1}{2}\right)^{5} \times\left(\frac{1}{2}\right)^{6}\)
సాధన.
\(\left(\frac{1}{2}\right)^{4+5+6}=\left(\frac{1}{2}\right)^{15}\)
= \(\frac{1}{2^{15}}\) [∵ a^m × aⁿ = a^m+n]

(ii) (-2)⁷ × (-2)³ × (-2)⁴
సాధన.
(-2)⁷⁺³⁺⁷ = (-2)¹⁴ = 2¹⁴
[∵ (-a)ⁿ = aⁿ, n ఒక సరిసంఖ్య ]

(iii) 4⁴ × \(\left(\frac{5}{4}\right)^{4}\)
సాధన.
\(4^{4} \times \frac{5^{4}}{4^{4}}=5^{4}\)
[∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\)]

(iv) \(\left[\frac{5^{-4}}{5^{-6}}\right] \times 5^{3}\)
సాధన.
= 5^-4 × (5⁶ × 5³) [∵ \(\frac{1}{a^{-n}}=a^{n}\)]
= 5^-4 × 5⁶⁺³ [∵ a^m × aⁿ = a^m+n]
= 5^-4 × 5⁹ = 5^(-4)+9 = 5⁵

(v) (-3)⁴ × 7⁴
సాధన.
= 3⁴ × 7⁴ [∵ 4 ఒక సరి సంఖ్య ]
= (3 × 7)⁴ = (21)⁴ [∵ a^m × b^m = (ab)^m]

3. సూక్ష్మీకరింపుము.
(i) \(2^{2} \times \frac{3^{2}}{2^{-2}} \times 3^{-1}\)
సాధన.
= 2² × 2² × 3² ×3^-1 [∵ \(\frac{1}{a^{-n}}=a^{n}\)]
= 2²⁺² × 3^2+(-1)
= 2⁴ × 3¹ = 16 × 3 = 48

(ii) (4^-1 × 3^-1) ÷ 6^-1
సాధన.
= \(\left(\frac{1}{4} \times \frac{1}{3}\right) \div \frac{1}{6}\) [∵ \(a^{-n}=\frac{1}{a^{n}}\)]
= \(\frac{1}{12}+\frac{1}{6}\)
= \(\frac {6}{12}\)
= \(\frac {1}{2}\)
= 2^-1

4. సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
(i) (4⁰ + 5^-1) × 5² × \(\frac {1}{3}\)
సాధన.

(ii) \(\left(\frac{1}{2}\right)^{-3} \times\left(\frac{1}{4}\right)^{-3} \times\left(\frac{1}{5}\right)^{-3}\)
సాధన.

(iii) (2^-1 + 3^-1 + 4^-1) × \(\frac {3}{4}\)
సాధన.

(iv) \(\frac{3^{-2}}{3} \times\left(3^{0}-3^{-1}\right)\)
సాధన.

(v) 1 + 2^-1 + 3^-1 + 4⁰
సాధన.

(vi) \(\left[\left(\frac{3}{2}\right)^{-2}\right]^{2}\)
సాధన.

5. సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
(i) \(\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}\)
(ii) ((5²)³ × 5⁴) ÷ 5⁶
సాధన.
(i) \(\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}\)
= \(\left[5 \times \frac{5}{1}\right]^{2}\)
= (5²)² = 5⁴ = 625 [∵ (a^m)ⁿ = a^mn]

(ii) ((5²)³ × 5⁴) ÷ 5⁶
సాధన.

6. కింది వానిలో ‘n’ విలువను కనుగొనుము.
(i) \(\left(\frac{2}{3}\right)^{3} \times\left(\frac{2}{3}\right)^{5}=\left(\frac{2}{3}\right)^{n-2}\)
సాధన.

భూములు సమానమైన ఘాతాంకాలు సమానాలు.
⇒ n – 2 = 8 ⇒ n = 8 + 2 = 10
∴ n = 10

(ii) (-3)ⁿ⁺¹ × (-3)⁵ = (-3)^-4
సాధన.
⇒ (-3)ⁿ⁺¹⁺⁵ = (-3)^-4 [∵ a^m x aⁿ = a^m+n]
⇒ (-3)ⁿ⁺⁶ = (-3)^-4
⇒ n + 6 = -4
n = – 4 – 6 = – 10
∴ n = – 10

(iii) 7²ⁿ⁺¹ ÷ 49 = 7³
సాధన.

7. 2^-3 = \(\frac{1}{2^{x}}\) అయిన x విలువను కనుగొనుము.
సాధన.
2^-3 = \(\frac{1}{2^{x}}\) = 2^-x [∵ \(\frac{1}{a^{n}}=a^{-n}\)]
⇒ 2^-3 = 2^-x
⇒ -x = -3
∴ x = 3

8. \(\left[\left(\frac{3}{4}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\right] \times\left(\frac{3}{5}\right)^{-2}\) సూక్ష్మీకరించుము.
సాధన.

9. m = 3 మరియు n = 2 అయిన ఈ క్రింది వాని విలువలను కనుగొనుము.
i) 9m² – 10n³
ii) am²n²
iii) 2m³ + 3n² – 5m²n
iv) mⁿ – n^m
సాధన.
i) 9m² – 10n³ = 9(3)² – 10(2)³
= 9 × 9 – 10 × 8
= 81 – 80 = 1

ii) 2m²n²
= 2(3)²(2)²
= 2 × 9 × 4
= 72

iii) 2m³ + 3n² – 5m²n
= 2(3)³ + 3(2)² – 5(3)² × 2
= (2 × 27) + (3 × 4) – (5 × 9 × 2)
= 54 + 12 – 90
= 66 – 90
= – 24

iv) mⁿ – n^m = 3² – 2³
= 3 × 3 – 2 × 2 × 2 = 9 – 8 = 1

10. \(\left(\frac{4}{7}\right)^{-5} \times\left(\frac{7}{4}\right)^{-7}\) సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
సాధన.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు InText Questions

ఇవి చేయండి

1. 8 సెం.మీ. పొడవు గల ఒక జత కర్రపుల్లలు తీసుకోండి. అదేవిధంగా 6 సెం.మీ. పొడవు గల మరొక జత కర్రపుల్లలు తీసుకోండి. వీటితో ఒక దీర్ఘచతురస్రాకారాన్ని 6 సెమీ) ఏర్పరచండి. ఈ దీర్ఘ చతురస్రం ఇవ్వబడిన 4 కొలతలతో (పుల్లలు) ఏర్పడింది. దీనిని వెడల్పు పుల్ల వెంబడి నెమ్మదిగా, కదిలించండి. ఏర్పడిన ఈ కొత్త రకం ఆకారం పూర్వపు ఆకారమేనా ? పటం (ii) లో ఏర్పడిన చతుర్భుజానికి కొత్త రూపం వచ్చింది కదా ! ముందు దీర్ఘచతురస్రం ఇప్పుడు సమాంతర చతుర్భుజం అయింది. నీవు ఏమైన కర్రపుల్లల కొలతలు మార్చావా ? లేదు కదా ! భుజాల పొడవులు అదేవిధంగా ఉన్నాయి. కొత్తగా ఏర్పడిన చతుర్భుజ రూపాన్ని మరొకసారి వ్యతిరేక దిశలో కదిలించండి. చతుర్భుజా ఏ రూపం వచ్చింది ? తిరిగి మరలా సమాంతర చతుర్భుజం వచ్చింది. కాని ఇది పూర్తిగా వొక రూపం అని పటం (iii) చూసి గమనించవచ్చు. ఈ సందర్భంలోనూ నాలుగు కొలతలు ఒకే విధంగా ఉన్నాయి. దీనిని బట్టి నాలుగు కొలతలతో ఏకైక చతుర్భుజం ఏర్పడదని తెలుసుకోవచ్చు. మరి అయిదు కొలతలు ఒక ఏకైక చతుర్భుజాన్ని ఏర్పరుస్తాయా? తిరిగి మనం కృత్యాన్ని కొనసాగిద్దాం . 8 సెం.మీ., 6 సెం.మీ. పొడవులు గల రెండు జతల పుల్లలతో దీర్ఘచతురస్రాన్ని ఏర్పరిచారు కదా ! పటం (iv) లో చూపిన విధంగా BD పొడవుకు సమానమయ్యే మరొక కర్రపుల్లను చేరుద్దాం. ఇప్పుడు ముందుగా చేసినట్లుగా వెడల్పు వెంబడి కదిపి చూడండి. ఆకారంలో మార్పు వచ్చిందా ? లేదు కదా! మార్పు చెందలేదని గమనిస్తారు. అందుచే ఐదవ కొలత (పుల్ల) దీర్ఘ చతురస్రాకారాన్ని మార్చడానికి వీలు లేకుండా చేయగలిగింది. మరొక రకమైన చతుర్భుజం ఏర్పడే అవకాశం లేకుండా ‘ (కొలతలు మార్చనంత వరకు) జరిగింది. దీనిని బట్టి ఒక చతుర్భుజం ఏకైకంగా ఏర్పడాలంటే ఐదు కొలతలు అవసరమని తెలుస్తున్నది. మరి. ఏ ఐదు కొలతలైనా ఏకైక చతుర్భుజాన్ని ఏర్పరచడానికి సరిపోతాయా ? (పేజీ నెం. 60)


సాధన.
అవును, సరిపోతాయి.

2. కావల్సిన సామగ్రి : కొలబద్ద, మూలమట్టాలు మరియు కోణమానిని. (పేజీ నెం. 61)
గుర్తుంచుకోవల్సినవి : రేఖలు సమాంతరాలో కాదో తెలుసుకొనుటకు మూలమట్టాలను మొదటి రేఖ నుండి రెండవ రేఖ వైపు జరపాలి.
కింది పటాలలో ధర్మాలను పరిశీలించడానికి తగు పరికరాలు ఎంచుకొని పరిశోధించి రాయండి.

ప్రతి చతుర్భుజానికి
a) ఎదుటి భుజాలు సమాంతరమో, కాదో చూడాలి.
b) ప్రతి కోణం కొలత కనుగొనాలి.
c) ప్రతి భుజం పొడవు కనుగొనాలి.

మీరు పరిశోధించి కనుగొన్న ఫలితాలను పట్టికలో నమోదు చేయండి.

సాధన.

3. 60° కోణాన్ని గీయగలరా ? (పేజీ నెం. 63)

సాధన.
వృత్తలేఖిని, స్కేలును ఉపయోగించి 60° కోణాన్ని నిర్మించవచ్చు.

4. BELT సమాంతర చతుర్భుజాన్ని, మరి ఏ ఇతర సమాంతర చతుర్భుజ ధర్మాల ఆధారంగా నిర్మించవచ్చో తెలిపి, నిర్మించి చూడండి. (పేజీ నెం. 75)
సాధన.
ఒక భుజం, ఒక కర్ణము, ఒక కోణం ఆధారంగా సమాంతర చతుర్భుజాన్ని నిర్మించవచ్చు.
BE = 5 సెం.మీ. ⇒ LT = 5 సెం.మీ.
∠B = 110° ⇒ ∠E = 180° – 110° = 70°
TE = 7.2 సెం.మీ.

ప్రయత్నించండి (పేజీ నెం. 70)

1. BA = 5 సెం.మీ., AT = 6 సెం.మీ. మరియు AS = 6.5 సెం.మీ. కొలతలతో BATS సమాంతర చతుర్భుజం గీయగలమా? వివరించండి.
సాధన.
BATS సమాంతర చతుర్భుజంలో ఎదురెదురు భుజాలు సమానాలు.
∴ BA = ST = 5 సెం.మీ., AT = BS = 6 సెం.మీ., AS = 6.5 సెం.మీ.
∴ BATS సమాంతర చతుర్భుజాన్ని నిర్మించవచ్చు.
ఎందుకనగా దీనికి 3 స్వతంత్ర కొలతలు చాలు.

2. ఒక విద్యా ర్థి PL = 3 సెం.మీ., LA = 4 సెం.మీ., AY = 4.5 సెం.మీ., PY = 2 సెం.మీ. మరియు LY = 6 సెం.మీ. కొలతలతో PLAY అనే చతుర్భుజాన్ని నిర్మించడానికి ప్రయత్నించాడు. కాని సాధ్యం కాలేదు. ఎందుకు ? నీవు కూడా చతుర్భుజాన్ని గీయడానికి ప్రయత్నించి, తగు కారణాలు తెల్పండి.
సాధన.
PLAY అను చతుర్భుజ కొలతలు
PL = 3 సెం.మీ.
LA = 4 సెం.మీ.
AY = 4.5 సెం.మీ.
PY = 2 సెం.మీ.
LY = 6 సెం.మీ.
ఇచ్చట YP + PL < YL
(త్రిభుజం YPL లో రెండు భుజాల మొత్తం 3వ భుజం కంటే ఎక్కువగా ఉండాలి. కానీ ఈ సందర్భంలో అలా సంభవించలేదు. )

PLAY అనునది ఒక చతుర్భుజం కాదు.
(∵ YL > YP)
∴ ఇచ్చిన కొలతలతో చతుర్భుజం నిర్మించలేము.
(ఎందుకనగా L నుండి గీసిన చాపము P నుండి గీసిన చాపములు ఖండించుకొనుటలేదు. Y, P, L లు ఒకే సరళరేఖపై కలవు. )

ఆలోచించి, చర్చించి వ్రాయండి (పేజీ నెం. 63)

1. ప్రతి దీర్ఘచతురస్రం ఒక సమాంతర చతుర్భుజమేనా ? ప్రతి సమాంతర చతుర్భుజం ఒక దీర్ఘచతురస్రమేనా ?
సాధన.
అవును. ప్రతి దీర్ఘచతురస్రం ఒక సమాంతర చతుర్భుజం అగును. కాని ప్రతి సమాంతర చతుర్భుజం ఒక దీర్ఘ చతురస్రం కాదు.

2. ఉమ బెల్లం చక్కని దీర్ఘచతురస్రాకారంలో చేయాలనుకున్నది. అది దీర్ఘచతురస్రాకారంలోనే వుండాలంటే ఆమె దానిని ఎన్ని రకాలుగా పరిశీలించి ఆకారం తీసుకురావాలి ?
సాధన.
బెల్లం చక్కీని దీర్ఘచతురస్రాకారంలోనికి మార్చాలంటే దానిని i) చతుర్భుజం ii) సమలంబ చతుర్భుజం iii) సమాంతర చతుర్భుజాకారాలను పరిశీలించాలి.

3. AB = 4.5 సెం.మీ., BC = 5.2 సెం.మీ., CD = 4.8 సెం.మీ., కర్ణాలు AC = 5 సెం.మీ. మరియు BD = 5.4 సెం.మీ. కొలతలు గల ABCD చతుర్భుజాన్ని గీయడానికి ముందుగా ΔABDతో మొదలు పెట్టి నాల్గవ శీర్షం ‘C’ ని గుర్తించగలరా ? కారణాలు తెలపండి. (పేజీ నెం. 72)
సాధన.
ΔABD నిర్మించడం సాధ్యం కాదు కావునా ముందుగా ΔABD తో మొదలు పెట్టి ABCD చతుర్భుజాన్ని నిర్మించడం సాధ్యం కాదు. [∵ AD పొడవు ఇవ్వబడలేదు)

4. PQ = 3 సెం.మీ., RS = 3 సెం.మీ., PS = 7.5 సెం.మీ., PR = 8 సెం.మీ. మరియు SQ = 4 సెం.మీ. కొలతలతో PORS చతుర్భుజం నిర్మించండి. నిర్మాణం ఏవిధంగా చేస్తారో వివరించండి. (పేజీ నెం. 72)
సాధన.
PQ = 3 సెం.మీ. RS = 3 సెం.మీ. PS = 7.5 సెం.మీ. PR = 8 సెం.మీ. SQ = 4 సెం.మీ.

∴ ఇచ్చిన కొలతలతో PQS త్రిభుజం నిర్మించలేము.
PQ+ QS < PS
∴ S శీర్షం నిర్మించవలెనన్న P నుండి గీసిన చాపం మరియు Q నుండి గీసిన చాపాలు ఖండించుకొనుట లేదు.
∴ S శీర్షం లేకుండా PQRS చతుర్భుజ నిర్మాణం సాధ్యం కాదు.

5. ప్రక్క పటంలో ఇచ్చిన కొలతలలో ∠P = 75°కు బదులు ∠P= 100° తీసుకుంటే PQRS చతుర్భుజం నిర్మించగలరా ? కారణాలు తెలపండి. (పేజీ నెం. 74)
సాధన.
PQ = 4 సెం.మీ., QR = 4.8 సెం.మీ.,
∠P = 100°, ∠Q = 100°, ∠R = 120°
∴ ఇచ్చిన కొలతలతో PQRS చతుర్భుజం నిర్మించ గలం. ఎందుకనగా 4 కోణాల మొత్తం = 360°

6. PL = 6 సెం.మీ., LA = 9.5 సెం.మీ., ∠P = 75°, L = 15° మరియు ∠A = 140° కొలతలతో PLAN చతుర్భుజం గీయగలరా ? (పేజీ నెం. 74)
(ప్రతి సందర్భంలోనూ చిత్తు పటాలను గీచి, కొలతలను విశ్లేషించండి.) మీ యొక్క సమాధానాలకు తగిన కారణాలు తెలపండి.
సాధన.
PL = 6 సెం.మీ., LA = 9.5 సెం.మీ., ∠P = 75°, ∠L = 15°, ∠A = 140°

∴ ఇచ్చిన కొలతలతో PLAN చతుర్భుజం నిర్మించలేము.

7. AB = 5 సెం.మీ., BC = 4.5 సెం.మీ., CD = 6 సెం.మీ., ∠B = 100°, ∠C = 75° కొలతలు గల ABCD చతుర్భుజాన్ని BC భూమిగా తీసుకొని (AB భూమిగా కాకుండా) నిర్మించగలరా ? చిత్తుపటం గీచి నిర్మాణ సోపానాలను వివరించుము. (పేజీ నెం. 77)
సాధన.
AB = 5 సెం.మీ., BC = 4.5 సెం.మీ., CD = 6 సెం.మీ., ∠B = 100°, ∠C = 75°
నిర్మాణ క్రమం :
1. 4.5 సెం.మీ.ల వ్యాసార్ధంతో BC రేఖాఖండాన్ని నిర్మించితిని.
2. B, C లు కేంద్రాలుగా 100°; 75° వరుస కిరణాలు గీచితిని.
3. B, C లు కేంద్రాలుగా 5 సెం.మీ., 6 సెం.మీ., వ్యాసార్ధాలతో రెండు చాపాలను గీయగా అవి కిరణాలను ఖండించిన బిందువులను A, D లుగా గుర్తించితిని.
4. A, D లను కలిపితిని.
5. ∴ ABCD చతుర్భుజం ఏర్పడినది.

8. ప్రక్క పటంలో ABCD రాంబస్ ను AC భూమిగా తీసుకొని నిర్మించగలరా ? లేదంటే కారణాలు తెలపండి. (పేజీ నెం. 79)

సాధన.

ABCD రాంబస్ లో AC భూమి కాకుండా BD ను భూమిగా తీసుకొని రాంబసను నిర్మించవచ్చు.

9. రాంబస్ లో రెండు కర్ణాల పొడవులు సమానం అయితే ఏ పటం ఏర్పడుతుంది ? చిత్తుపటం గీచి, తగు కారణాలను తెలపండి. (పేజీ నెం. 79)
(లేదా )
ఒక సమాంతర చతుర్భుజంలోని కర్ణాల పొడవులు సమానం అయిన సందర్భంలో ఏయే పటాలు ఏర్పడునో చిత్తు పటాలు గీచి, తగు కారణాలతో తెల్పండి.
సాధన.
ఒక రాంబ లోని రెండు కర్ణాల పొడవులు సమానం అయిన రాంబస్లో అన్ని భుజాలు సమానంగా ఉంటాయి కావునా అది ఒక చతురస్రం అవుతుంది. ∴ ABCD ఒక చతురస్రం.
[∵ AB = BC = CD = DA & AC = BD]

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.6 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.6

కింది ఇవ్వబడిన కొలతలతో కావల్సిన చతుర్భుజాలు నిర్మించండి.

(a) CART రాంబలో CR = 6 సెం.మీ., AT = 4.8 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{CR}}\) కర్ణాన్ని నిర్మించితిని.

2. \(\overline{\mathrm{CR}}\) వ్యాసార్ధంలో సగం కంటే ఎక్కువ వ్యాసార్ధం తీసుకొని, C, R కేంద్రాల నుండి పైన, క్రింద గీచిన చాపాల ఖండన బిందువులు P, Q లుగా గుర్తించవలెను. P, Qలను కలుపగా CRకు లంబ సమద్విఖండన రేఖ ఏర్పడినది. వీటి ఖండన బిందువును ‘O’ గా గుర్తించితిని.
3. AT = 4.8 సెం.మీ. వ్యాసార్ధంలో సగం వ్యాసార్ధం 2.4 సెం.మీ.లతో ‘O’ కేంద్రంగా రెండు చాపాలను పైన క్రింద గీయగా అవి లంబ సమద్విఖండన రేఖ \(\overline{\mathrm{PQ}}\)ను A, T ల వద్ద ఖండించుకొనును.
4. C, T లను, C, A లను, R, T లను, R, A లను కలిపితిని.
∴ CART రాంబస్ ఏర్పడినది.

(b) SOAP రాంబస్ లో SA = 4.3 సెం.మీ., OP = 5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 4.3 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{SA}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. 4.3 సెం.మీ. వ్యాసార్ధంలో సగానికంటే ఎక్కువ వ్యాసార్ధంతో S, Aల నుండి పైన క్రింద చాపాలను గీయగా, వాటి ఖండన బిందువులు X, Y లుగా గుర్తించితిని. X, Y లను కలిపితిని.
3. \(\overline{\mathrm{XY}}\), \(\overline{\mathrm{SA}}\) కు ఒక లంబ సమద్విఖండన రేఖ. వీటి ఖండన బిందువును ‘M’ గా గుర్తించితిని.
4. ‘M’ కేంద్రంగా OP వ్యాసార్ధంలో సగం వ్యాసార్ధం 2.5 సెం.మీ.లతో పైన క్రింది గీచిన చాపాలు O, P లవద్ద \(\overline{\mathrm{XY}}\) ను ఖండించినవి.

5. S, P లను S, Oలను మరియు P, Aలను, O, A లను కలిపితిని.
6. ∴ SOAP రాంబస్ ఏర్పడినది.

(c) JUMP చతురస్రంలో కర్ణం 4.2 సెం.మీ.
సాధన.
JM = UP = 4.2 సెం.మీ.
[∵ చతురస్రంలోని కర్ణాలు సమానాలు]

నిర్మాణ క్రమం :
1. 4.2 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{JM}}\) రేఖాఖండాన్ని (కర్ణం) నిర్మించితిని.
2. \(\overline{\mathrm{JM}}\) వ్యాసార్ధంలో సగాని కంటే ఎక్కువ వ్యాసార్ధంతో J, M కేంద్రాల నుండి పైన, క్రింద గీచిన చాపాల ఖండన బిందువులను X, Y లుగా గుర్తించితిని.
3. X, Y లను కలిపితిని. \(\overline{\mathrm{XY}}\), \(\overline{\mathrm{JM}}\) కు ఒక లంబ సమద్విఖండన రేఖ. ఇది \(\overline{\mathrm{XY}}\) ను ‘O’ వద్ద ఖండిస్తుంది.
4. ‘O’ కేంద్రంగా \(\overline{\mathrm{UP}}\) వ్యాసార్ధంలో సగం వ్యాసార్థంతో పైన, క్రింద గీచిన చాపాలు \(\overline{\mathrm{XY}}\) ను U, Pల వద్ద ఖండించును.
5. J, U లను, U, M లను మరియు J, P లను, M, P లను కలిపితిని.
∴ చతురస్రం JUMP ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.5 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.5

కింది చతుర్భుజాలను ఇవ్వబడిన కొలతలతో నిర్మించండి.

(a) PQRS చతుర్భుజంలో PQ = 3.6 సెం.మీ., QR = 4.5 సెం.మీ., RS = 5.6 సెం.మీ., ∠PQR = 135° మరియు ∠QRS = 60°.
సాధన.
నిర్మాణ క్రమం :
1. 3.6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{PQ}}\) రేఖాఖండాన్ని నిర్మించితిని.

2. Q కేంద్రంగా 135° కిరణాన్ని, 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
3. R కేంద్రంగా 60° ల కిరణాన్ని, 5.6 సెం.మీ. వ్యాసార్ధంతో ఒక చాపం గీయగా, వాటి ఖండన బిందువును ‘S’ గా గుర్తించితిని.
4. R, S లను కలిపితిని.
∴ PQRS చతుర్భుజం ఏర్పడినది.

(b) LAMP చతుర్భుజంలో AM = MP = PL = 5 సెం.మీ., ∠M = 90° మరియు ∠P = 60°.
సాధన.
నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{AM}}\) రేఖాఖండాన్ని గీచితిని.

2. M కేంద్రంగా 90° కోణంతో ఒక కిరణాన్ని, 5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును P గా గుర్తించితిని.
3. P కేంద్రంగా 60° కోణంతో ఒక కిరణాన్ని, 5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును L గా గుర్తించితిని.
4. A, L లను కలిపితిని.
∴ LAMP చతుర్భుజం ఏర్పడినది.

(c) ABCD ట్రెపీజియం (సమలంబ చతుర్భుజం)లో AB//CD, AB = 8 సెం.మీ., BC = 6 సెం.మీ., CD = 4 సెం.మీ., మరియు ∠B = 60°.
సాధన.
\(\overline{\mathrm{AB}}\)//\(\overline{\mathrm{CD}}\) అయిన ∠B + ∠C = 180°
⇒ ∠C = 180° – 60° = 120 ∴ ∠C = 120°

నిర్మాణ క్రమం :
1. 8 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. ‘B’ కేంద్రంగా 60° ల కిరణాన్ని, 6 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘C’ గా గుర్తించితిని.
3. ‘C’ కేంద్రంగా 120° లతో ఒక కిరణాన్ని, 4 సెం.మీ.లతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘D’ గా గుర్తించితిని.
4. A, Dలను కలిపితిని.
∴ ABCD ట్రెపీజియం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.4

కింది ఇవ్వబడిన కొలతలను ఉపయోగించి కావాల్సిన చతుర్భుజాలను నిర్మించండి.

(a) చతుర్భుజం HELP లో HE = 6 సెం.మీ., EL = 4.5 సెం.మీ., ∠H = 60°, ∠E = 105° మరియు ∠P = 120.
సాధన.
HELP చతుర్భుజంలో
HE = 6 సెం.మీ. EL = 4.5 సెం.మీ.
∠H = 60°, ∠E = 105°, ∠P = 120°
⇒ ∠L = 360° – (60° + 105° + 120°)
= 360° – 285° = 750

నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{HE}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. E కేంద్రంగా 105° కిరణాన్ని, 4.5 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాల ఖండన బిందువును ‘L’ గా గుర్తించితిని.
3. H, L లు కేంద్రాలుగా 60°, 75°లతో వరుసగా రెండు కిరణాల ఖండన బిందువును ‘P’ గా గుర్తించితిని.
4. H, P లను, P, L లను కలిపితిని.
∴ HELP చతుర్భుజం ఏర్పడినది.

(b) సమాంతర చతుర్భుజం GRAM లో GR = AM = 5 సెం.మీ., RA = MG = 6.2 సెం.మీ. మరియు ∠R = 85°.
సాధన.
GRAM సమాంతర చతుర్భుజంలో
GR = AM = 5 సెం.మీ. RA = MG = 6.2 సెం.మీ. ∠R = 85°
నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్థంతో \(\overline{\mathrm{GR}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. R కేంద్రంగా 85° కోణంతో గీచిన కిరణాన్ని, 6.2 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపం ఖండించిన, ఖండన బిందువును ‘A’ గా గుర్తించితిని.
3. G, A లు కేంద్రాలుగా వరుసగా 6.2 సెం.మీ., 5 – సెం.మీ.లతో గీచిన చాపాల ఖండన బిందువును ‘M’ గా గుర్తించితిని.

4. G, M లను, A, M లను కలిపి తిని.
5. ∴ GRAM సమాంతర చతుర్భుజం ఏర్పడినది.

(c) దీర్ఘచతురస్రం FLAG లో భుజం FL = 6 సెం.మీ., మరియు LA = 4.2 సెం.మీ.
సాధన.
FL = AG = 6 సెం.మీ.
LA = FG = 4.2 సెం.మీ. ∠F = ∠L = 90°
(∵ దీర్ఘచతురస్రంలో ఎదురెదురు భుజాలు సమానాలు. ప్రతి కోణం 90° ఉంటుంది.)

నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{FL}}\) రేఖాఖండాన్ని గీచితిని.
2. F కేంద్రంగా 90° లతో ఒక కిరణాన్ని మరియు 4.2 సెం.మీ.లతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘G’ గా గుర్తించితిని.
3. L కేంద్రంగా 90° లతో ఒక కిరణాన్ని మరియు 4.2 సెం.మీ.లతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘A’ గా గుర్తించితిని.
4. G, A లను కలిపితిని.
5. ∴ GRAM దీర్ఘచతురస్రం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.3

కింది ఇవ్వబడిన కొలతలను ఉపయోగించి కావల్సిన – చతుర్భుజాలను నిర్మించండి.

(a) GOLD అనే చతుర్భుజంలో OL = 7.5 సెం.మీ., GL = 6 సెం.మీ., LD = 5 సెం.మీ., DG = 5.5 సెం.మీ. మరియు OD = 10 సెం.మీ
సాధన.
నిర్మాణ క్రమం :
1. 7.5 సెం.మీ. వ్యాసార్థంతో \(\overline{\mathrm{OL}}\) రేఖాఖండాన్ని గీచితిని.
2. O, L లు కేంద్రాలుగా వరుసగా 10 సెం.మీ., 5 సెం.మీ.లతో గీచిన చాపాల ఖండన బిందువును ‘D’ గా గుర్తించితిని.

3. L, D లు కేంద్రాలుగా వరుసగా 6 సెం.మీ., 5.5 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘G’ గా గుర్తించితిని.
4. O, G లను, L, G లను, O, D లను, L, D లను, G, D లను కలిపితిని.
∴ GOLD అను ఒక చతుర్భుజం ఏర్పడినది.

(b) PQRS చతుర్భుజంలో PQ = 4.2 సెం.మీ., QR = 3 సెం.మీ., PS = 2.8 సెం.మీ., PR= 4.5 సెం.మీ. మరియు QS = 5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 4.2 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{PQ}}\) రేఖాఖండాన్ని నిర్మించితిని.

2. P, Qలు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘R’ గా గుర్తించితిని. P, R మరియు Q, Rలను కలిపితిని.
3. Q, Pలు కేంద్రాలుగా వరుసగా 5 సెం.మీ., 2.8 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపరేఖల ఖండన బిందువును ‘S’ గా గుర్తించితిని. P, S లను, Q, S లను, S, Rలను కలిపితిని.
∴ PORS అను ఒక చతుర్భుజం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.2

కింద ఇవ్వబడిన కొలతలను ఉపయోగించి చతుర్భుజాల నిర్మాణాలను చేయండి.

(a) ABCD చతుర్భుజములో AB = 4.5 సెం.మీ., BC = 5.5 సెం.మీ., CD = 4 సెం.మీ., AD = 6 సెం.మీ., మరియు AC = 7 సెం.మీ.
సాధన.

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. A, B లు కేంద్రాలుగా వరుసగా 7 సెం.మీ., 5.5 సెం.మీ. వ్యాసార్దాలుగా గీచిన చాపాల ఖండన బిందువు ‘C’ గా గుర్తించితిని.
3. A. C లను, B, C లను కలిపితిని.
4. C, A లు కేంద్రాలుగా వరుసగా 4 సెం.మీ., 6 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువు ‘D’ గా గుర్తించితిని.
5. D, C లను, A, D లను కలిపితిని.
∴ ABCD చతుర్భుజం ఏర్పడినది.

(b) PQRS చతుర్భుజములో PQ = 3.5 సెం.మీ., QR = 4 సెం.మీ., RS = 5 సెం.మీ., PS = 4.5 సెం.మీ., మరియు QS = 6.5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 3.5 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{PQ}}\) రేఖాఖండాన్ని గీచితిని.

2. P, Q లు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 6.5 సెం.మీ. లచే రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘S’ గా గుర్తించితిని.
3. S, Q లు కేంద్రాలుగా 5 సెం.మీ., 4 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాలు ఖండించుకొనగా, వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
4. P, S లను Q, S లను కలిపితిని. అదేవిధంగా S, Rలను Q, Rలను కలిపితిని.
∴ చతుర్భుజం PARS ఏర్పడినది.

(c) సమాంతర చతుర్భుజం ABCD లో AB = 6.సెం.మీ., BC = 4.5 సెం.మీ. మరియు BD = 7.5 సెం.మీ.
సాధన.
ABCD సమాంతర చతుర్భుజంలో
AB = CD = 6 సెం.మీ.
BC = AD = 4.5 సెం.మీ.

నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని గీచితిని.
2. A, B లు కేంద్రాలుగా 4.5 సెం.మీ., 7.5 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాల ఖండన బిందువులను ‘D’ గా గుర్తించితిని. A, D మరియు B, D లను కలిపితిని.
3. D, B లు కేంద్రాలుగా 6. సెం.మీ., 4.5 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘C’ గా గుర్తించితిని.
4. B, C మరియు D, C లను కలిపితిని.
∴ సమాంతర చతుర్భుజం ABCD ఏర్పడినది.

(d) సమచతుర్భుజం (రాంబస్) NICE లో NI = 4 సెం.మీ. మరియు IE = 5.6 సెం.మీ.
సాధన.
NI = IC = CE = NE = 4 సెం.మీ., IE = 5.6 సెం.మీ.

నిర్మాణ క్రమం :
1. 4 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{NI}}\) రేఖాఖండాన్ని గీచితిని.
2. N, I లు కేంద్రాలుగా వరుసగా 4 సెం.మీ., 5.6 సెం.మీ. వ్యాసార్ధాలతో రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘E’ గా గుర్తించితిని. N, E మరియు I, E లను కలిపితిని.
3. E, Iలు కేంద్రాలుగా వరుసగా 4 సెం.మీ., వ్యాసార్ధాలతో గీచిన రెండు చాపాల ఖండన బిందువును ‘C’ గా గుర్తించితిని.
4. E, C లను, I, C లను కలిపితిని.
∴ NICE రాంబస్ ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.1

కింద ఇవ్వబడిన కొలతలను ఉపయోగించి చతుర్భుజాల నిర్మాణాలను చేయండి. నిర్మాణ క్రమం రాయండి.

(a) ABCD చతుర్భుజంలో AB = 5.5 సెం.మీ., BC = 3.5 సెం.మీ., CD = 4 సెం.మీ., AD = 5 సెం.మీ., మరియు ∠A = 45°.
సాధన.
ABCD చతుర్భుజంలో AB = 5.5 సెం.మీ.,
BC = 3.5 సెం.మీ., CD = 4 సెం.మీ.,
AD = 5 సెం.మీ., A = 45°

నిర్మాణ క్రమం :
1. 5.5 సెం.మీ. వ్యాసార్ధం గల \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని గీచితిని.
2. A కేంద్రంతో 45° కిరణాన్ని, 5 సెం.మీ.ల చాపాన్ని గీయగా వాటి ఖండన బిందువు ‘D’గా గుర్తించితిని.
3. D, B లు కేంద్రాలు వరుసగా 4 సెం.మీ., 3.5 సెం.మీ.ల వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువు ‘C’.
4. DC మరియు BC లను కలిపితిని.
∴ ABCD చతుర్భుజం ఏర్పడినది.

(b) BEST చతుర్భుజంలో BE = 2.9 సెం.మీ., ES = 3.2 సెం.మీ., ST = 2.7 సెం.మీ., BT = 3.4 సెం.మీ., మరియు ∠B = 75°.
సాధన.
BEST చతుర్భుజంలో BE = 2.9 సెం.మీ.,
ES = 3.2 సెం.మీ., ST = 2.7 సెం.మీ.,
BT = 3.4 సెం.మీ., ∠B = 75°

నిర్మాణ క్రమం :
1. 2.9 సెం.మీ. వ్యాసార్థం గల BE రేఖాఖండాన్నినిర్మించితిని.
2. B కేంద్రంగా 75° కోణంతో ఒక కిరణాన్ని, 3.4 సెం.మీ. వ్యాసార్థంతో ఒక చాపాన్ని గీయగా అవి ఖండించుకొన్న ఖండన బిందువు T గా గుర్తించితిని.
3. T, E లు కేంద్రాలుగా 2.7 సెం.మీ., 3.2 సెం.మీ.లతో వరుసగా రెండు చాపాలను గీయగా వాటి ఖండన బిందువు ‘S’ గా గుర్తించితిని.
4. T, S మరియు E, S లను కలిపితిని.
∴ BEST చతుర్భుజం ఏర్పడినది.

(c) సమాంతర చతుర్భుజం PQRS లో PQ = 4.5 సెం.మీ., QR = 3 సెం.మీ. మరియు ∠PQR = 60°.
సాధన.
PQ = 4.5 సెం.మీ., QR = 3 సెం.మీ. మరియు ∠PQR = 60°.
⇒ RS = 4.5 సెం.మీ. మరియు PS = 3 సెం.మీ. [∵ ఎదురెదురు భుజాలు సమానాలు]

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{PQ}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. Q కేంద్రంగా 60° కోణంతో ఒక కిరణాన్ని, 3 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
3. R, P లు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలుగా రెండు చాపాలను గీయగా వాటి ఖండన బిందువు ‘S’ గా గుర్తించితిని.
4. P, Sలను; S, Rలను కలుపగా PQRS సమాంతర చతుర్భుజం ఏర్పడినది.

(d) రాంబస్ MATH లో AT = 4 సెం.మీ., ∠MAT = 120°.
సాధన.
రాంబస్ లో అన్ని భుజాలు సమానాలు కావున
MA = 4 సెం.మీ., AT = 4 సెం.మీ., TH = 4 సెం.మీ., MH = 4 సెం.మీ.,
∠MAT = 120°.

నిర్మాణ క్రమం :
1. 4 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{MA}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. A కేంద్రంగా 120° కోణంతో ఒక కిరణాన్ని, 4 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘T’ గా గుర్తించితిని.
3. M, T లు కేంద్రాలుగా 4 సెం.మీ. వ్యాసార్ధంతో రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘H’ గా గుర్తించితిని.
4. M, H లను, T, H లను కలపగా MATH రాంబస్ ఏర్పడినది.

(e) దీర్ఘచతురస్రం FLAT లో FL = 5 సెం.మీ., LA = 3 సెం.మీ.
సాధన.
దీర్ఘచతురస్రం FLAT లో FL = AT = 5 సెం.మీ.,
LA = TF = 3 సెం.మీ., ∠F = ∠L= ∠A = ∠T = 90°

నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{FL}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. F కేంద్రంగా 90° ల కిరణాన్ని, 3 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘T’ గా గుర్తించితిని.
3. T, L కేంద్రాల నుండి వరుసగా 5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలతో చాపాలు గీయగా ఏర్పడిన ఖండన బిందువును ‘A’ గా గుర్తించితిని.
4. T, A లను, L, A లను కలిపితిని.
∴ FLAT దీర్ఘచతురస్రం ఏర్పడినది.

(f) చతురస్రం LUDO లో LU = 4.5 సెం.మీ.
సాధన.
చతురస్రం LUDO లో LU = UD = DO = LO = 4.5 సెం.మీ.

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంగా LU రేఖాఖండాన్ని గీచితిని.
2. Lకేంద్రంగా 90° కిరణాన్ని మరియు 4. 5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీచితిని. అలాగే U కేంద్రంగా 90° కిరణాన్ని మరియు 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీచితిని. వాటి ఖండన బిందువులను వరుసగా O,Dలుగా గుర్తించితిని.
3. O, D లను కలిపితిని.
∴ LUDO చతురస్రం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు InText Questions

ఇవి చేయండి (పేజీ నెం. 35)

ఈ క్రింది వానిలో ఏవి రేఖీయ సమీకరణాలు :
(i) 4x + 6 = 8
(ii) 4x – 5y = 9
(iii) 5x + 6xy – 4y² = 16
(iv) xy + yz + zx = 11
(v) 3x + 2y – 6 = 0
(vi) 3 = 2x + y
(vii) 7p+ 6q + 13s = 11
సాధన.
(i), (ii), (v), (vi) (vii) లు రేఖీయ సమీకరణాలు ఎందుకనగా ఆ సమీకరణాలలో ప్రతిదాని యొక్క పరిమాణం ఒకటి (1).

ఇవి చేయండి (పేజీ నెం. 36)

ఈ క్రింది వానిలో ఏవి సామాన్య సమీకరణాలు ?
(i) 3x + 5 = 14
(ii) 3x – 6 = x + 2
(iii) 3 = 2x + y
(iv) \(\frac{x}{3}\) + 5 = 0
(v) x² + 5x + 3 = 0
(vi) 5m – 6n = 0
(vii) 7p+ 6q + 13s = 11
(viii) 13t – 26 = 39
సాధన.
(i) 3x + 5 = 14
(ii) 3x – 6 = x + 2
(iv) \(\frac{x}{3}\) + 5 = 0
(viii) 13t – 26 = 39 లు సామాన్య సమీకరణాలు ఎందుకనగా ఇవి ax + b = 0 రూపంలో కలవు.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.5 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.5

ప్రశ్న 1.
క్రింది సమీకరణాలను సాధించుము.
(i) \(\frac{n}{5}-\frac{5}{7}=\frac{2}{3}\)
సాధన.

(ii) \(\frac{x}{3}-\frac{x}{4}=14\)
సాధన.
\(\frac{4 x-3 x}{12}\) = 14 ⇒ \(\frac{\mathrm{x}}{12}\) = 14
⇒ x = 12 × 14 = 168
∴ x = 168

(iii) \(\frac{z}{2}+\frac{z}{3}-\frac{z}{6}=8\)
సాధన.
\(\frac{3 z+2 z-z}{6}\) = 8

(iv) \(\frac{2 p}{3}-\frac{p}{5}=11 \frac{2}{3}\)
సాధన.

(v) \(9 \frac{1}{4}=y-1 \frac{1}{3}\)
సాధన.

(vi) \(\frac{x}{2}-\frac{4}{5}+\frac{x}{5}+\frac{3 x}{10}=\frac{1}{5}\)
సాధన.

(vii) \(\frac{x}{2}-\frac{1}{4}=\frac{x}{3}+\frac{1}{2}\)
సాధన.

(viii) \(\frac{2 x-3}{3 x+2}=\frac{-2}{3}\)
సాధన.
⇒ 3(2x – 3) = – 2(3x + 2)
⇒ 6x – 9 = – 6x – 4
⇒ 6x + 6x = – 4 + 9
⇒ 12x = 5
∴ x = \(\frac {5}{12}\)

(ix) \(\frac{8 p-5}{7 p+1}=\frac{-2}{4}\)
సాధన.
\(\frac{8 p-5}{7 p+1}=\frac{-1}{2}\)
⇒ 2(8p – 5) = -(7p + 1)
⇒ 16p – 10 = – 7p – 1
⇒ 16p + 7p = – 1 + 10
⇒ 23p = 9
∴ p = \(\frac {9}{23}\)

(x) \(\frac{7 y+2}{5}=\frac{6 y-5}{11}\)
సాధన.
⇒ 11(7y + 2) = 5 (6y – 5)
⇒ 77y + 22 = 30y – 25
⇒ 77y – 30y = – 25 – 22
⇒ 47y = – 47 ⇒ y = \(\frac {-47}{47}\)
∴ y = -1

(xi) \(\frac{x+5}{6}-\frac{x+1}{9}=\frac{x+3}{4}\)
సాధన.

⇒ 4(x + 13) = 18 (x + 3)
⇒ 4x + 52 = 18x + 54
⇒ 4x – 18x = 54 – 52
⇒ – 14x = 2

(xiii) \(\frac{3 t+1}{16}-\frac{2 t-3}{7}=\frac{t+3}{8}+\frac{3 t-1}{14}\)
సాధన.

– 11t – 38t = 34 – 55
= – 49t = – 21

ప్రశ్న 2.
ఒక సంఖ్య యొక్క 3వ భాగము దాని 5వ భాగము కంటే 4 ఎక్కువ అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
x యొక్క 3వ భాగం = \(\frac{x}{3}\)
x యొక్క 5వ భాగం = \(\frac{x}{5}\)

ప్రశ్న 3.
రెండు ధనసంఖ్యల భేదం 36. ఒక దానిని రెండవ దానితో భాగించగా వచ్చే భాగఫలం 4 అయిన వానిని కనుగొనుము.
(సూచన : ఒక సంఖ్య ‘x’ అనుకొనిన రెండవ సంఖ్య ‘x – 36’)
సాధన.
రెండు ధనసంఖ్యలు x, (x – 36) అనుకొనుము.
ఒక దానిని రెండవ దానితో భాగించగా వచ్చు భాగఫలం 4 అయిన
⇒ \(\frac{x}{x-36}\) ⇒ 4 = x = 4(x – 36)
⇒ x = 4x – 144 ⇒ 4x – x = 144
⇒ 3x = 144 ⇒ x = 48
∴ ఆ ధనసంఖ్యలు = x, x – 36 = 48, 12.

ప్రశ్న 4.
ఒక భిన్నంలో లవం, హారం కంటే 4 తక్కువ. అయితే లవ, హారాలకు ఒకటి కలిపిన అది \(\frac {1}{2}\) కు సమానము అవుతుంది. అయిన ఆ భిన్నమును కనుగొనుము.
సాధన.
ఒక భిన్నం \(\frac{x}{y}\) అనుకొనుము.
∴ లవం, హారం కంటే 4 తక్కువ అయిన లవం (x) = y – 4 అగును.
భిన్నం = \(\frac{y-4}{y}\)
లెక్క ప్రకారం \(\frac{y-4+1}{y+1}=\frac{1}{2}\) ⇒ \(\frac{y-3}{y+1}=\frac{1}{2}\)
⇒ 2 = 2(y – 3) = y + 1
⇒ 2(y – 6) = y + 1
⇒ 2y – y = 1 + 6 ⇒ y = 7
∴ కావలసిన భిన్నం = \(\frac{y-4}{y}=\frac{7-4}{7}=\frac{3}{7}\)

ప్రశ్న 5.
మూడు వరుస సంఖ్యలను 10, 17, 26 లచే భాగించినపుడు భాగఫలాల మొత్తం 10ని ఇచ్చే మూడు వరుస సంఖ్యలను కనుగొనుము.
(సూచన : మూడు వరుస సంఖ్యలను x, x + 1, x + 2 అనుకొనిన, \(\frac{x}{10}+\frac{x+1}{17}+\frac{x+2}{26}\) = 10)
సాధన.
మూడు వరుస సంఖ్యలు x, (x + 1), (x + 2) లు అనుకొనుము.,
x, (x + 1), (x + 2) లను 10, 17, 26 లచే
భాగించగా వచ్చు భాగఫలాల మొత్తం 10 అయిన

⇒ 221x + 130x + 130 + 85x + 170 = 22,100
⇒ 436x + 300 = 22,100
⇒ 436x = 22,100 – 300

∴ కావలసిన 3 వరుస సంఖ్యలు = 50, 51, 52.

ప్రశ్న 6.
40 మంది విద్యార్థులు గల తరగతిలో, బాలికల సంఖ్య, బాలుర సంఖ్యలో \(\frac {3}{5}\)వ వంతు అయిన బాలుర సంఖ్యను కనుగొనుము.
సాధన.
తరగతిలోని విద్యార్థుల సంఖ్య = 40
బాలుర సంఖ్య = x అనుకొనుము.

ప్రశ్న 7.
15 సం॥ల తరువాత మేరి వయస్సు, ప్రస్తుత వయస్సుకు 4 రెట్లు. అయిన మేరి ప్రస్తుత వయస్సు ఎంత ?
సాధన.
మేరి ప్రస్తుత వయస్సు = x అనుకొనుము.
15 సం॥ల తరువాత మేరి వయస్సు = (x + 15) సం॥లు
లెక్క ప్రకారం (x + 15) = 4 × x ⇒ x + 15 = 4x
⇒ 4x – x = 15 ⇒ 3x = 15
⇒ x = 5
∴ మేరి ప్రస్తుత వయస్సు = 5 సం॥లు.

ప్రశ్న 8.
అరవింద్ దగ్గర వున్న కిడ్డీ బ్యాంక్ లో రూపాయి నాణెములు, అర్ధ రూపాయి నాణెములు గలవు. అర్ధ రూపాయి నాణెముల సంఖ్య, రూపాయి నాణెముల సంఖ్యకు 3 రెట్లు. నాణెముల మొత్తం విలువ ₹ 35 అయిన ఏఏ రకం నాణెములు ఎన్నెన్ని గలవు ?
సాధన.
రూపాయి నాణేల సంఖ్య = x అనుకొనుము.
అర్ధ రూపాయి నాణేల సంఖ్య = 3 × x = 3x
నాణేల మొత్తం విలువ = ₹ \(\frac{3 x}{2}\) + x
∴ లెక్క ప్రకారం \(\frac{3 x}{2}\) + x = 35

∴ రూపాయి నాణేల సంఖ్య = 14
అర్ధ రూపాయి నాణేల సంఖ్య = 3x = 3 × 14 = 42

ప్రశ్న 9.
A మరియు B లు కలసి ఒక పనిని 12 రోజులలో పూర్తి చేయగలరు. A ఒక్కడే ఆ పనిని 20 రోజులలో పూర్తి చేసిన B ఒక్కడే ఆ పనిని ఎన్ని రోజులలో పూర్తి చేయగలడు ?
సాధన.
A, B లు ఒక పనిని 12 రోజులలో పూర్తి చేయగలిగిన,
వారు ఇరువురూ ఒక రోజులో చేసే పని = \(\frac {1}{2}\)
A అదే పనిని 20 రోజులలో పూర్తి చేయగలిగిన, అతని 1 రోజు పని = \(\frac {1}{20}\)
∴ B ఒక రోజు పని = \(\frac{1}{12}-\frac{1}{20}\)
= \(\frac{5-3}{60}\)
= \(\frac {2}{60}\)
= \(\frac {1}{30}\) వ వంతు
∴ ఆ పనిని పూర్తి చేయుటకు B కి పట్టు రోజులు = 30 రోజులు

ప్రశ్న 10.
ఒక రైలు 40 కి.మీ./గంట వేగంతో ప్రయాణించిన గమ్యస్థానమును 11 నిమిషాలు ఆలస్యంగా చేరును. ఒకవేళ 50 కి.మీ./గంట వేగంతో ప్రయాణించిన 5 నిమిషాలు ఆలస్యంగా చేరును. అయిన రైలు ప్రయాణించవలసిన దూరమును కనుగొనుము.
సాధన.
చేరవలసిన గమ్యస్థానం యొక్క దూరం = x కి.మీ. అనుకొనుము.
40 కి.మీ./గంట వేగంతో ‘x’ కి.మీ. ప్రయాణించుటకు పట్టు కాలం = \(\frac{x}{40}\) గం॥
50 కి.మీ./గంట వేగంతో ప్రయాణించుటకు పట్టు కాలం = \(\frac{x}{50}\) గం॥
కానీ దత్తాంశం ప్రకారం ఈ రెండింటి మధ్య తేడా = 11 – 5 = 6 ని॥ = \(\frac{6}{60}\) గంటలు

ప్రశ్న 11.
ఒక జింకల గుంపులో \(\frac{1}{4}\)వ భాగము అడవికి వెళ్ళినాయి. మొత్తంలో \(\frac{1}{3}\) వ భాగము పచ్చిక మైదానంలో వున్నాయి. మిగిలిన 15 నది ఒడ్డున నీరు త్రాగుతున్నాయి. అయిన మొత్తం జింకల సంఖ్యను కనుగొనుము.
సాధన.
జింకల సంఖ్య = x అనుకొనుము.
అడవికి వెళ్ళిన జింకల సంఖ్య = \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
పచ్చిక మైదానంలోని జింకల సంఖ్య = \(\frac{1}{4}\) × x = \(\frac{1}{4}\)
∴ మిగిలిన జింకల సంఖ్య =

కాని, లెక్క ప్రకారం మిగిలిన జింకల సంఖ్య = 15
∴ \(\frac{5 x}{12}\) = 15

∴ మొత్తం జింకల సంఖ్య = 36

ప్రశ్న 12.
ఒక దుకాణదారుడు ఒక రేడియోను ₹ 903 లకు అమ్మటం వల్ల అతను 5% లాభాన్ని పొందుతాడు. అయిన రేడియో యొక్క కొన్నవెలను కనుగొనుము.
సాధన.
రేడియో అమ్మినవెల (S.P.) = ₹ 903
లాభశాతం = 5%
కోన్నవెల (C.P.) = ?

ప్రశ్న 13.
శేఖర్ తన వద్ద వున్న మిఠాయిలలో పావు భాగము రేణుకు, 5 మిఠాయిలు రాజికి ఇచ్చాడు. ఇంకా తన వద్ద 7 మిఠాయిలు మిగిలి వున్న అతని వద్ద మొదట వున్న మిఠాయిలు ఎన్ని ?
సాధన.
శేఖర్ వద్ద వున్న మిఠాయిల సంఖ్య = x అనుకొనుము.
రేణుకకు ఇచ్చిన భాగం = \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
రాజికి ఇచ్చిన మిఠాయిల సంఖ్య = 5
ఇంకా తన వద్ద నున్న మిఠాయిల సంఖ్య = 7
లెక్క ప్రకారం


∴ శేఖర్ వద్ద మొదట ఉన్న మిఠాయిల సంఖ్య = 16