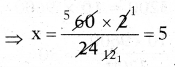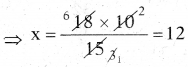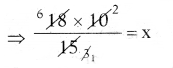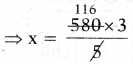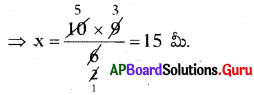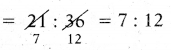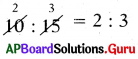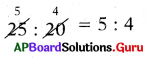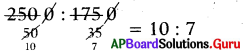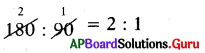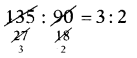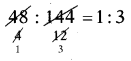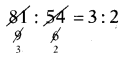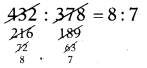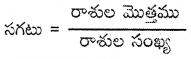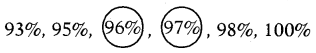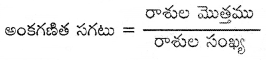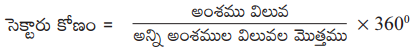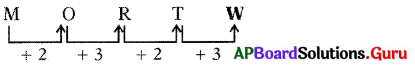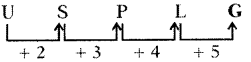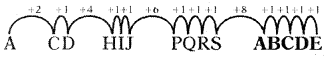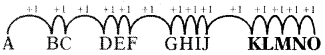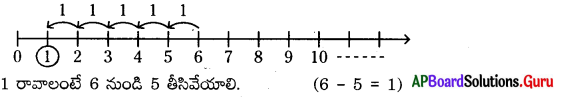Mahesh

SCERT AP 7th Class Maths Solutions Pdf Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.3 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson నిష్పత్తి మరియు అనుపాతం Exercise 7.3

ప్రశ్న1.
ఈ క్రింద ఇవ్వబడిన రాశులు అనులోమానుపాతంలో ఉంటాయో, లేదా విలోమానుపాతంలో ఉంటాయో కనుక్కోండి:
(i) నిర్దిష్ట దూరాన్ని చేరుటకు పట్టు సమయం, వేగం.
సాధన :
విలోమానుపాతంలో ఉంటాయి.

(ii) స్థలం వైశాల్యం, దాని ఖరీదు.
సాధన :
అనులోమానుపాతంలో ఉంటాయి.

(iii) పనిని పూర్తి చేయుటకు మనుషుల సంఖ్య, పని పూర్తవడానికి పట్టు సమయం.
సాధన :
విలోమానుపాతంలో ఉంటాయి.

(iv) మనుషుల సంఖ్య, ఒక్కొక్కరికి వచ్చే ఆహారధాన్యాల పరిమాణం (మొత్తం ఆహార ధాన్యాలు స్థిరం).
సాధన :
విలోమానుపాతంలో ఉంటాయి.

(v) బస్సులో ప్రయాణం చేసే దూరం, టికెట్ ధర.
సాధన :
అనులోమానుపాతంలో ఉంటాయి.

ప్రశ్న2.
24 మంది వ్యక్తులు ఒక గోడను 10 రోజులలో నిర్మించగలరు. అంతే పొడవైన గోడను 15 మంది వ్యక్తులు ఎన్ని రోజులలో నిర్మించగలరు ?
సాధన :
వ్యక్తుల సంఖ్య, గోడ నిర్మాణం పూర్తికావడానికి పట్టు రోజుల సంఖ్య విలోమానుపాతంలో ఉంటాయి. (మనుషుల సంఖ్య ↑, రోజుల సంఖ్య ↓)
24 మంది వ్యక్తులు ఒక గోడను నిర్మించుటకు పట్టు రోజులు = 10
15 మంది అంతే పొడవుగల గోడను నిర్మించుటకు పట్టు రోజులు = x అనుకొందాము.

24 : 15 = x : 10
మధ్యమముల లబ్దం = అంత్యముల లబ్దం
= 15 × x = 24 × 10

విలోమానుపాతంలో కలవు కావున లబ్దం ఎల్లప్పుడు స్థిరం.
24 × 10 = 15 × x

= 16 . 151
∴ x = 16
∴ 15 మంది వ్యక్తులు ఆ గోడను 16 రోజులలో నిర్మించగలరు.

ప్రశ్న3.
ఒక బాలికల వసతి గృహంలో, 50 మంది బాలికలకు 40 రోజులకు సరిపోయే ఆహార పదార్థాలు ఉన్నాయి. అదనంగా 30 మంది బాలికలు ప్రవేశం పొందిన, అందరికీ ఎన్ని రోజుల వరకూ ఆ ఆహార పదార్థాలు
సరిపోతాయి ?
సాధన :
వసతి గృహంలో బాలికల సంఖ్య, వారికి ఆహారం సరిపడు రోజుల సంఖ్య విలోమానుపాతంలో ఉంటాయి.
50 మంది బాలికలకు ఆహారం సరిపడు రోజులు = 40 అదనంగా 30 మంది బాలికలు ప్రవేశం పొందినచో వసతి గృహంలో 50 + 30 = 80 మంది బాలికలు ఉంటారు.
80 మంది బాలికలకు ఆహారం సరిపడు రోజులు = x అనుకొందాము.

50 : 80 = x : 40
మధ్యమముల లబ్దం = అంత్యముల లబ్దం
⇒ 80 × x = 50 × 40

(లేదా)
విలోమానుపాతంలో ఉంటే లబ్ధం ఎల్లప్పుడు స్థిరము.
⇒ 50 × 40 = 80 × x

వసతి గృహంలోని 80 బాలికలకు 25 రోజుల వరకు ఆహార పదార్థాలు సరిపోతాయి.

ప్రశ్న4.
సుమన్ కొంత దూరం గంటకు 48 కి.మీ. సరాసరి వేగంతో, ఐదు గంటలపాటు ప్రయాణించాడు. అదే దూరాన్ని అతను నాలుగు గంటలలో ప్రయాణం చేయవలెనన్న, ఎంత వేగంతో ప్రయాణం చేయాలి ?
సాధన :
స్థిర దూరాన్ని ప్రయాణించుటకు వేగం, కాలం విలోమానుపాతంలో ఉంటాయి.
4 గంటలలో ఆ దూరాన్ని పూర్తి చేయుటకు అతని వేగం = x కి.మీ./గం. అనుకొనుము.

48: x = 4 : 5
⇒ x × 4 = 48 × 5

(లేదా)
విలోమానుపాతంలో ఉంటే లబ్దం ఎల్లప్పుడు స్థిరం.
48 × 5 = x × 4

⇒ x = 60 కి.మీ./గం.
∴ 4 గంటల ప్రయాణంలో ఆ దూరాన్ని చేరుటకు సుమన్ గంటకు 60 కి.మీ. వేగంతో ప్రయాణం చేయాలి.

ప్రశ్న5.
ఒక్కొక్క సైకిలు వెల ₹ 4500 చొప్పున, ఎనిమిది సైకిళ్లను కొనుటకు ఒక వ్యక్తి వద్ద డబ్బులు ఉన్నవి. ఒక్కొక్క సైకిల్ వెల ₹500 తగ్గిన, తన వద్దవున్న అదే సొమ్ముతో అతను ఎన్ని సైకిళ్లను కొనగలడు ?

సాధన :
సైకిళ్ళ సంఖ్య మరియు వాని వెల విలోమానుపాతంలో ఉంటాయి.
₹4500 వెల నుండి ₹500 తగ్గినచో ఒక్కొక్క సైకిల్ వెల = 4500 – 500 = ₹4000
₹4000 వెలతో కొనగల సైకిళ్ళ సంఖ్య = X అను||

4500: 4000 = x : 8
⇒ 4000 × x = 4500 × 8

(లేదా)
4500 × 8 = 4000 × x
⇒ \(\frac{4500 \times 8}{4000}\) = x
⇒ 9 = x
∴ ఒక్కొక్క సైకిల్ వెల ₹500 తగ్గినచో అతను తన వద్ద గల సొమ్ముతో 9 సైకిళ్ళు కొనగలడు.

ప్రశ్న6.
2 పంపులు ఒక నీళ్ల ట్యాంకును, ఒక గంట సమయంలో నింపగలవు. అదే నీళ్ళ ట్యాంక్ ను 24 ని.లలో నింపవలెనన్న ఎన్ని పంపులు కావలెను ?
సాధన :
పంపుల సంఖ్య, ట్యాంకును నింపు సమయం విలోమానుపాతంలో ఉంటాయి.
24 నిమిషాలలో ట్యాంకును నింపుటకు అవసరమగు పంపులు = x అనుకొనుము.

2 : x = 24 : 60
⇒ 24 × x = 60 × 2

(లేదా)
2 × 60 = x × 24
⇒ \(\frac{2 \times 60}{24}\) = x
⇒ 5 = x
∴ నీళ్ళ ట్యాంకు 24 నిమిషాలలో నింపుటకు 5 పంపులు అవసరము.

ప్రశ్న7.
18 మంది వ్యక్తులు ఒక పొలంలో పంటను 10 రోజులలో కోయగలరు. అదే పంటను 15 రోజులలో కోయవలెనన్న, ఎంత మంది మనుషులు కావలెను ?

సాధన :
వ్యక్తుల సంఖ్య, పంటను కోయు రోజులు విలోమాను పాతంలో ఉంటాయి.
15 రోజులలో పంట కోయుటకు కావలసిన మనుషులు = x అనుకొందాము.

18 : x = 15 : 10
⇒ 15 × x = 18 × 10

(లేదా)
⇒ 18 × 10 = x × 15

⇒ x = 12
∴ 15 రోజులలో పంట కోయుటకు 12 మంది మనుషులు కావలెను.

ప్రశ్న8.
ఒక సరిహద్దు చెక్ పోస్ట్ వద్ద 1200 మంది సైనికులకు 28 రోజులకు సరిపోయే ఆహార పదార్థాలు ఉన్నాయి. 4 రోజుల తర్వాత కొంతమంది సైనికులు వేరొక చెక్ పోస్టు బదిలీకాగా, మిగిలిన వారికి 32 రోజులకు ఆహార పదార్థాలు సరిపోయాయి. అయిన ఎంత మంది సైనికులు బదిలీ అయ్యారు ?

సాధన :
1200 మంది సైనికులకు ఆహారం సరిపోవు రోజులు = 28
4 రోజుల తరువాత 1200 మంది సైనికులకు ఆహారం – సరిపోవు రోజులు = 28 – 4 = 24
4 రోజుల తరువాత ‘x’ మంది సైనికులు బదిలీ అయినారు అనుకొందాము.

ఇప్పుడు సైన్యంలోని సైనికుల సంఖ్య 1200 – x.
వీరికి ఆహారం సరిపోవు రోజులు = 32
సైనికుల సంఖ్య, వారికి ఆహారం సరిపోవు రోజుల సంఖ్య విలోమానుపాతంలో ఉంటాయి.

1200 : 1200 – x = 32 : 24
(1200 – x) 32 = 1200 × 24

⇒ 1200 – x = 900
⇒ 1200 – 900 = x
∴ 300 = X
(లేదా)
1200 × 24 = (1200 – x)32
⇒ \(\frac{1200 \times 24}{32}\) = 1200 – x
⇒ 900 = 1200 – x
⇒ x = 1200 – 900
⇒ x = 300
∴ బదిలీ అయిన సైనికుల సంఖ్య = 300

SCERT AP 7th Class Maths Solutions Pdf Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.2 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson నిష్పత్తి మరియు అనుపాతం Exercise 7.2

ప్రశ్న1.
ఈ క్రింద ఇవ్వబడిన రాశులు అనులోమానుపాతంలో ఉన్నాయో, లేదో కనుగొనండి
(i) పెన్నుల వెల, పెన్నుల సంఖ్య.
సాధన :
అనులోమానుపాతంలో ఉంటాయి.

(ii) మనుషుల సంఖ్య, వారికి కావాల్సిన ఆహారం.
సాధన :
అనులోమానుపాతంలో ఉంటాయి.

(iii) కారు వేగం, గమ్యాన్ని చేరడానికి పట్టే సమయం.
సాధన :
అనులోమానుపాతంలో ఉండవు.

(iv) పట్టిన సమయం, ప్రయాణించిన దూరం.
సాధన :
అనులోమానుపాతంలో ఉంటాయి.

(v) కూరగాయల వెల, బ్యాగుల సంఖ్య.
సాధన :
చెప్పలేము.

ప్రశ్న2.
ఐదుగురు వ్యక్తులు ఒక పార్కుకు వెళ్ళి టికెట్ల కొరకు ₹ 580 చెల్లించారు. అదే పార్కుకు ముగ్గురు వ్యక్తులు వెళ్తే టికెట్ల కొరకు ఎంత సొమ్ము చెల్లించాలి ?

సాధన :
వ్యక్తుల సంఖ్య, వారు చెల్లించే టికెట్ సొమ్ము
అనులోమానుపాతంలో ఉంటాయి. ఐదుగురు వ్యక్తులు చెల్లించిన టికెట్ సొమ్ము = ₹580
ముగ్గురు వ్యక్తులు చెల్లించాల్సిన సొమ్ము= ₹x అనుకొందాం.
5:580 = 3 : x [∵ అనులోమానుపాతంలో కలవు]
అంత్యముల లబ్దం = మధ్యమముల లబ్దం
5 × x = 580 × 3

⇒ x = 348
∴ ముగ్గురు వ్యక్తులు చెల్లించాల్సిన టికెట్ సొమ్ము
= ₹ 348.

ప్రశ్న3.
ఒక మ్యాపులో 26 కి.మీ.ను ఒక సెం.మీ. ప్రామాణికంగా గీశారు. రెండు ప్రాంతాల మధ్య వాస్తవ దూరం 1404 కి.మీ. అయిన, మ్యాచ్లో వాటి మధ్య దూరం “ఎంత ఉంటుంది ?
సాధన :
మ్యాపులో ఉన్న దూరం, వాస్తవ దూరానికి అనులోమాను
పాతంలో ఉంటుంది. మ్యాప్ లో రెండు ప్రాంతాల మధ్య దూరం = x సెం.మీ. అనుకుంటే
1:26000 = x : 1404000
∴ 1 : 26 = x : 1404 అంత్యముల లబ్దం = మధ్యమముల లబ్దం
[∵ అనులోమానుపాతంలో కలవు]
⇒ 1 × 1404 = 26 × x

∴ మ్యాప్ లో ఆ రెండు ప్రాంతాల మధ్య దూరం
x = 54 సెం.మీ.

ప్రశ్న4.
72 పైపుల బరువు 180 కి.గ్రా. అయిన అటువంటి 90 పైపుల బరువు ఎంత ?

సాధన :
పైపుల సంఖ్య మరియు పైపుల బరువులు అనులోమాను పాతంలో ఉంటాయి.
72 పైపుల బరువు = 180 కి.గ్రా.
90 పైపుల బరువు = x కి.గ్రా.
అనుకొనుము. :: 72 : 180 = 90 : x
అంత్యముల లబ్దం = మధ్యమముల లబ్దం
72 × x = 180 × 90

∴ 90 పైపుల బరువు = 225 కి.గ్రా.

ప్రశ్న5.
ఒక మోటార్ సైకిల్ 135 కి.మీ. దూరాన్ని చేరుటకు సరాసరిన 3 లీ. పెట్రోలు అవసరమైన, 495 కి.మీ. దూరాన్ని చేరుటకు ఎన్ని లీటర్ల పెట్రోల్ అవసరం అవుతుంది ?
సాధన :
మోటార్ సైకిల్ ప్రయాణించిన దూరం, అందుకు అవసరమైన పెట్రోలు అనులోమానుపాతంలో ఉంటాయి.
ఒక మోటార్ సైకిల్ 135 కి.మీ. దూరాన్ని చేరుటకు అవసరమగు సరాసరి పెట్రోలు = 3 లీ.
495 కి.మీ. దూరాన్ని ప్రయాణించుటకు అవసరమైన పెట్రోలు = x కి.మీ. అనుకొందాము.
∴ 135 : 3 = 495 : 1
అంత్యముల లబ్దం = మధ్యమముల లబ్దం [∵ అనులోమానుపాతంలో కలవు]
⇒ 135 × x = 3 × 495

∴ 495 కి.మీ. ప్రయాణించుటకు అవసరమగు పెట్రోలు = 11 లీటర్లు.

ప్రశ్న6.
10 మీ. పొడవు కలిగిన ఒక స్థంభం యొక్క నీడ పొడవు 6 మీ. అదే సమయంలో మరొక స్థంభం యొక్క నీడ పొడవు 9 మీ. అయిన, ఆ స్థంభం యొక్క అసలు పొడవు ఎంత ?
సాధన :
ఒకే సమయంలో వివిధ స్థంభాల ఎత్తులు మరియు
అవి ఏర్పరిచే నీడల పొడవులు అనులోమానుపాతంలో ఉంటాయి.

10 మీ. ఎత్తు గల స్థంభం యొక్క నీడ పొడవు = 6 మీ.
9 మీ. నీడ పొడవు గల స్థంభం యొక్క ఎత్తు = x మీ. అనుకొందాం.

∴ 10: 6 = x:9
మధ్యమముల లబ్దం = అంత్యముల లబ్దం 6 × x = 10 × 9,

∴ 9 మీ. నీడ పొడవు గల స్థంభం ఎత్తు = 15 మీ.

SCERT AP 7th Class Maths Solutions Pdf Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.1 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson నిష్పత్తి మరియు అనుపాతం Exercise 7.1

ప్రశ్న1.
పవన్ మరియు రోషన్లు ఒక్కొక్కరు వరుసగా ₹ 1,50,000, ₹ 2,00,000తో ఒక వ్యాపారాన్ని ప్రారంభించారు. తొమ్మిది నెలల తర్వాత రోషన్ వ్యాపారం నుండి వైదొలిగాడు. సంవత్సరాంతమున వారికి ₹ 45,000 లాభం వచ్చింది. ఆ లాభంలో పవన్ మరియు రోషన్ల యొక్క వాటాలు ఎంత?
సాధన :
పవన్ పెట్టుబడి = ₹ 1,50,000
రోషన్ పెట్టుబడి = ₹ 2,00,000

పవన్, రోషన్ పెట్టుబడుల నిష్పత్తి = 1,50,000 : 2,00,000 = 3:4
పవన్ వ్యాపారంలో కొనసాగిన కాలం = 12 నెలలు
రోషన్ వ్యాపారంలో కొనసాగిన కాలం = 9 నెలలు

పవన్, రోషన్లు వ్యాపారంలో కొనసాగిన కాలముల నిష్పత్తి = 12 : 9 = 4 : 3
పవన్, రోషన్లు వారి యొక్క లాభాన్ని పెట్టుబడుల నిష్పత్తి మరియు కాలముల నిష్పత్తుల యొక్క బహుళ నిష్పత్తిలో పంచుకోవాలి.
∴ బహుళ నిష్పత్తి = 3 ×.4 : 4 × 3
= 12 : 12 = 1 : 1

లాభం ₹ 45,000 ను వారు 1 : 1 నిష్పత్తిలో (సమానంగా) పంచుకోవాలి.
∴ లాభంలో పవన్ యొక్క వాటా
= 45,000 × \(\frac{1}{2}\) = ₹ 22,500

లాభంలో రోషన్ యొక్క వాటా
= 45,000 × \(\frac{1}{2}\) = ₹ 22,500

ప్రశ్న2.
సల్మాన్ ₹75,000 పెట్టుబడితో ఒక హోటల్ ప్రారంభించాడు. 5 నెలల తర్వాత దీపక్ ఆ వ్యాపారంలో ₹ 80,000 పెట్టుబడితో చేరాడు. సంవత్సరాంతమున వారు ₹ 73,000 లాభాన్ని సంపాదించగా, ఆ లాభంలో వారి యొక్క వాటాలు ఎలా పంచుకొంటారు?
సాధన :
సల్మాన్ పెట్టుబడి = ₹75,000
దీపక్ పెట్టుబడి = ₹80,000 వారి పెట్టుబడుల నిష్పత్తి = 75,000 : 80,000
= 15: 16
సల్మాన్ వ్యాపారంలో కొనసాగిన కాలం = 12 నెలలు

దీపక్ వ్యాపారంలో కొనసాగిన కాలం
= 12 – 5 = 7 నెలలు

సల్మాన్ మరియు దీపక వ్యాపార కాలముల నిష్పత్తి
= 12:7
లాభాన్ని వారు పెట్టుబడులు మరియు కాలముల నిష్పత్తుల యొక్క బహుళ నిష్పత్తిలో పంచుకోవాలి.

లాభాన్ని సల్మాన్ మరియు దీపకు 45 : 28 నిష్పత్తిలో పంచుకొంటారు.
∴ లాభం ₹ 73,000 లో
సల్మాన్ వాటా = 73,000 × \(\frac{45}{45+28}\)
= 73,000 × \(\frac{45}{73}\) = ₹45,000
దీపక్ వాటా = 73,000 – 45,000 = ₹ 28,000

ప్రశ్న3.
రామయ్య తన యొక్క 24 ఆవులను మేపుటకుగాను ఒక పచ్చికబయలు అద్దెకు తీసుకున్నాడు. 5 నెలల తర్వాత సోమయ్య తన యొక్క 40 ఆవులను మేపుటకు అదే పచ్చికబయలు అద్దెకు తీసుకొనెను. సంవత్సరాంతమున వారిద్దరూ కలిసి ₹ 35,500 అద్దె చెల్లించిన, ఆ అద్దెలో వారిద్దరి భాగాలు ఎంతెంత ?

సాధన :
రామయ్య యొక్క ఆవుల సంఖ్య = 24
సోమయ్య యొక్క ఆవుల సంఖ్య = 40
వారి యొక్క ఆవుల సంఖ్య యొక్క నిష్పత్తి

పచ్చికబయలులో రామయ్య ఆవులను మేపిన కాలం
= 12 నెలలు

పచ్చికబయలులో సోమయ్య ఆవులను మేపిన కాలం
= 12 – 5 = 7 నెలలు

వారు ఆవులను మేపిన కాలముల నిష్పత్తి = 12 : 7
పచ్చికబయలు యొక్క అద్దెను వారు ఆవుల సంఖ్య . మరియు వాటిని మేపిన కాలముల నిష్పత్తి యొక్క బహుళ నిష్పత్తిలో చెల్లించాలి.
బహుళ నిష్పత్తి = 3 × 12 : 5 × 7 = 36 : 35

పచ్చికబయలు యొక్క సంవత్సర అద్దె ₹ 35,500 లో
∴ రామయ్య వాటా = 35,500 × \(\frac{36}{36+35} \)
= 35,500 × \(\frac{36}{71}\)
= ₹ 18,000

సోమయ్య వాటా = 35,500 – 18,000
= ₹ 17,500

ప్రశ్న4.
రవి ఒక వ్యాపారాన్ని ₹ 2,10,000తో ప్రారంభించాడు. కొన్ని నెలల తర్వాత, ప్రకాష్ అదే వ్యాపారంలో ₹ 3,60,000 పెట్టుబడితో ప్రవేశించాడు. సంవత్సరాంతమున వారిరువురుకు, ఒక్కొక్కరికి ₹1,20,000 లాభం వచ్చిన, ప్రకాష్ ఎన్ని నెలల తర్వాత ఆ వ్యాపారంలో చేరాడో కనుగొనండి.
సాధన :
రవి పెట్టుబడి = ₹ 2,10,000
ప్రకాష్ పెట్టుబడి = ₹3,60,000
వారి పెట్టుబడుల నిష్పత్తి = 210000 : 360000

రవి వ్యాపారంలో కొనసాగిన కాలం = 12 నెలలు

ప్రకాష్ వ్యాపారంలో కొనసాగిన కాలం = x నెలలు
అనుకొందాం. వారు వ్యాపారంలో కొనసాగిన కాలాల నిష్పత్తి
= 12 : x
వారి పెట్టుబడులు మరియు వ్యాపారంలో కొనసాగిన కాలముల నిష్పత్తుల బహుళ నిష్పత్తి

లాభాన్ని వారు పంచుకోవాల్సిన నిష్పత్తి = 7 : x
సంవత్సరాంతమున వారి లాభంలో ఒక్కొక్కరి వాటా = ₹1,20,000
వారి లాభాల నిష్పత్తి = 1,20,000 : 1,20,000
= 1:1
⇒ 7 : x = 1:1
⇒ 7 × 1 = x × 1
∴ 7 = x
ప్రకాష్ వ్యాపారంలో కొనసాగిన కాలం = 7 నెలలు

∴ ప్రకాష్ వ్యాపారంలో 12 -7 = 5 నెలల తరువాత చేరాడు.

SCERT AP 7th Class Maths Solutions Pdf Chapter 7 నిష్పత్తి మరియు అనుపాతం Review Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson నిష్పత్తి మరియు అనుపాతం Review Exercise

ప్రశ్న1.
క్రింది వాటి యొక్క నిష్పత్తి కనుగొనండి.
(i) 5, 8
సాధన :
5:8

(ii) ₹10, ₹15
సాధన :
₹10, ₹15

(iii) 25 కి.గ్రా., 20 కి.గ్రా.
సాధన :
25 కి.గ్రా., 20 కి.గ్రా.

(iv) 5 లీ., 500 మి.లీ.
సాధన :
5 లీ., 500 మి.లీ.
5000 మి.లీ. : 500 మి.లీ. (∵ 1 లీ. = 1000 మి.లీ.; 5 లీ. = 5000 మి.లీ.)

(v) 2 కి.మీ. 500 మీ., 1 కి.మీ. 750 మీ.
సాధన :
2 కి.మీ. 500 మీ., 1 కి.మీ. 750 మీ.
2000 మీ. + 500 మీ. : 1000 మీ. + 750 మీ. (∵ 1 కి.మీ. = 1000 మీ., 2 కి. మీ. = 2000 మీ.)

(vi) 3 గం., 1 గం. 30 ని.
సాధన :
3 గం., 1 గం. 30 ని.
3 × 60 నిమిషాలు, 60 + 30 = 90 నిమిషాలు 21

(vii) 40 రోజులు, 1 సంవత్సరం
సాధన :
40 రోజులు, 1 సాధారణ సంవత్సరం
40 రోజులు, 365 రోజులు

ప్రశ్న2.
క్రింది నిష్పత్తులను సూక్ష్మరూపంలో తెల్పండి.

(i) 120 : 130
సాధన :

(ii) 135 : 90
సాధన :

(iii) 48 : 144
సాధన :

(iv) 81 : 54
సాధన :

(v) 432 : 378
సాధన :

ప్రశ్న3.
క్రింది నిష్పత్తులు అనుపాతంలో ఉన్నాయో, లేదో పరీక్షించండి.
(i) 10:20, 25 : 50
సాధన :
10 : 20, 25 : 30
అంత్యముల లబ్దం = 10 × 50 = 500
మధ్యమముల లబ్ధం = 20 × 25 = 500
అంత్యముల లబ్ధం = మధ్యమముల లబ్ధం
∴ ఇచ్చిన నిష్పత్తులు అనుపాతంలో కలవు.

(ii) 18 : 12, 15 : 10
సాధన :
18 : 12, 15 : 10
అంత్యముల లబ్దం = 18 × 10 = 180
మధ్యమముల లబ్దం = 12 × 15 = 180
అంత్యముల లబ్ధం = మధ్యమముల లబ్ధం
∴ ఇచ్చిన నిష్పత్తులు అనుపాతంలో కలవు.

(iii) 25 : 20, 16 : 14
సాధన :
25 : 20, 16 : 14
అంత్యముల లబ్ధం = 25 × 14 = 350
మధ్యమముల లబ్దం = 20 × 16= 320
అంత్యముల లబ్ధం ≠ మధ్యమముల లబ్ధం
∴ ఇచ్చిన నిష్పత్తులు అనుపాతంలో లేవు.

(iv) 54 : 27, 18 : 9
సాధన :
54 : 27, 18 :9
అంత్యముల లబ్దం = 54 × 9 = 486
మధ్యమముల లబ్దం = 27 × 18 = 486
అంత్యముల లబ్ధం = మధ్యమముల లబ్ధం
∴ ఇచ్చిన నిష్పత్తులు అనుపాతంలో కలవు.

ప్రశ్న4.
ఈ క్రింది ఖాళీలను సరైన సంఖ్యలతో నింపండి.
(i) 15 : 19 = 45 : ___
సాధన :
15 : 19 = 45 : 57
[15 × 3 = 45, 19 × 3 = 57]

(ii) 9 : 13 = ___ : 65
సాధన :
9 : 13 = 45 : 65
[13 × 5 = 65, : 9 × 5 = 45]

(iii) 8: ___ = 72 : 63
సాధన :
8 : 7 = 72 : 63
[72 ÷ 9 = 8, ∴ 63 ÷ 9 = 7]

ప్రశ్న5.
3 : 4 కు సమానమైన నిష్పత్తులను, ఖాళీ పెట్టెలలో పూరించండి.

సాధన.

ప్రశ్న6.
ఈ క్రింద ఇవ్వబడిన సంఖ్యల నుండి ఏవైనా నాలుగు సంఖ్యలను ఎంచుకొని, అనుపాతంలో ఉన్నట్లుగా వాటిని అమర్చుము. 2, 3, 10, 12, 15, 18
ఉదా : 2 : 10 = 3:15
(i) : ________
(ii) : ________
సాధన :
ఇచ్చిన సంఖ్యలు 2, 3, 10, 12, 15, 18
(i) 10 : 12 = 15 : 18
(ii) 2 : 12 = 3:18 .

ప్రశ్న7.
₹1500 ను 7 : 3 నిష్పత్తిలో ఉండేలా రెండు భాగాలుగా విభజించండి.
సాధన :
నిష్పత్తిలోని పదాల మొత్తం 7 + 3 = 10
ఇచ్చిన సంఖ్య ₹ 1500 లో

ప్రశ్న8.
ఒక ప్యాకెట్ లో 20 చాక్లెట్లు ఉన్నాయి. రజని, రాగిణిలు వాటిని పంచుకొనగా, రజని 12 చాక్లెట్లు తీసుకుంది. అయిన రజని, రాగిణిల చాక్లెట్ల నిష్పత్తి ఎంత ?
సాధన :
ప్యాకెట్ లోని మొత్తం చాక్లెట్లు = 20
రజని తీసుకున్న చాక్లెట్లు = 12
రాగిణి తీసుకున్న చాక్లెట్లు = 8
రజని, రాగిణిలు పంచుకొన్న చాక్లెట్ల నిష్పత్తి

ప్రశ్న9.
ఒక గొట్టాన్ని రెండు భాగాలుగా చేయగా, మొదటి భాగానికి, రెండవ భాగానికి గల నిష్పత్తి 1 : 8. రెండవ భాగం పొడవు 48 సెం.మీ. అయిన మొదటి భాగం పొడవు ఎంత ? భాగాలు చేయకముందు గొట్టం మొత్తం పొడవు ఎంత? పొడవు ఎంత ?
సాధన :
మొదటి పద్దతి : గొట్టం యొక్క మొదటి భాగానికి మరియు రెండవ
భాగానికి గల నిష్పత్తి = 7:8 గొట్టం రెండవ భాగం పొడవు = 48 సెం.మీ.
మొదటి భాగం పొడవు = x సెం.మీ. అనుకొందాం.
∴x: 48 = 7:8
అంత్యముల లబ్ధం = మధ్యమముల లబ్ధం
⇒ x × 8 = 48 × 7

∴ గొట్టం యొక్క మొదటి భాగం పొడవు = x = 42 సెం.మీ.

∴ భాగాలు చేయకముందు గొట్టం యొక్క మొత్తం పొడవు = 42 + 48 = 90 సెం.మీ.
రెండవ పద్ధతి : గొట్టం యొక్క మొదటి, రెండవ భాగాల పొడవుల నిష్పత్తి
= 7 : 8

∴ మొదటి భాగం పొడవు = 7x
రెండవ భాగం పొడవు = 8x అనుకొందాం.
లెక్క ప్రకారం రెండవ భాగం = 8x = 48
⇒ x = \(\frac{48}{8}\) = 6
∴ మొదటి భాగం పొడవు = 7x
= 7 X 6 = 42 సెం.మీ.

భాగాలు చేయకముందు గొట్టం పొడవు
7x + 8x = 15x = 15 (6) = 90 సెం.మీ.

SCERT AP 7th Class Maths Solutions Pdf Chapter 6 దత్తాంశ నిర్వహణ InText Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 6th Lesson దత్తాంశ నిర్వహణ InText Questions

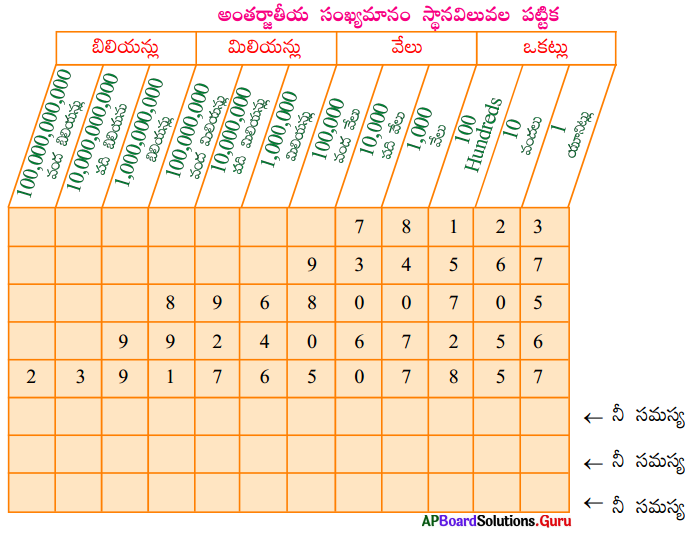
[పేజీ నెం. 216]

అంక సగటు ఏ విలువల మధ్య ఉంటుంది?
తెలుగు, హిందీ, ఇంగ్లీష్ సబ్జెక్టులలో సరళ, బిందు, గీత మరియు రేఖలు పొందిన మార్కుల వివరాలు క్రింద ఇవ్వబడ్డాయి.

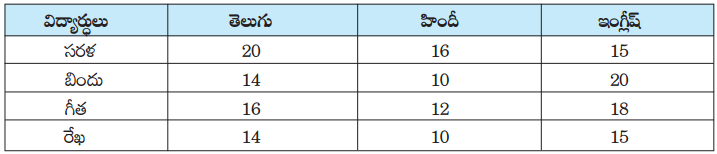
సాధన.
ప్రతీ సబ్జెక్టులో విద్యార్థులు పొందిన సరాసరి మార్కులు గణన చేద్దాం.

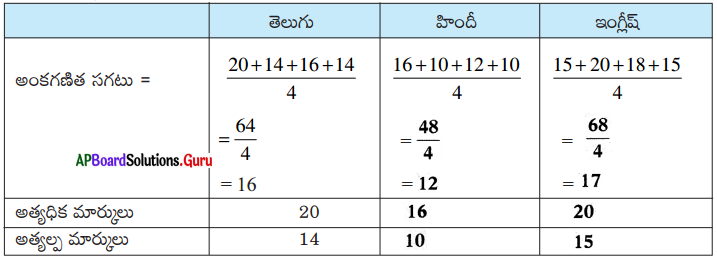
(i) పై పట్టిక నుండి, నీవు ఏమి గమనించావు ?
సాధన.
సగటు ఎల్లప్పుడూ గరిష్ఠ మరియు కనిష్ఠ విలువల మధ్య ఉంటుంది.

(ii) అన్ని సందర్భములలో అంకగణిత సగటు అత్యల్ప మరియు అత్యధిక పరిశీలనా విలువల మధ్య ఉన్నదా ?
సాధన.
అవును, అంకగణిత సగటు ఎల్లప్పుడూ అత్యల్ప మరియు అత్యధిక పరిశీలనా విలువల మధ్య ఉంటుంది.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 218]

ప్రశ్న 1.
5 యొక్క మొదటి మూడు గుణిజాల అంక గణిత సగటు కనుగొనుము.
సాధన.
5 యొక్క మొదటి మూడు గుణిజాలు 5, 10, 15.

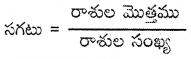
∴ 5, 10, 15 ల సగటు = \(\frac{5+10+15}{3}\) = \(\frac{30}{3}\) = 10

అన్వేషిద్దాం [పేజి నెం. 218]

తరగతిలోని 10 మంది విద్యార్థుల బరువులను (కిలోగ్రాములలో) సేకరించండి. క్రింది ప్రశ్నలకు సమాధానాలు రాయండి.

సాధన.

ప్రశ్న 1.
అత్యధిక మరియు అత్యల్ప బరువులు ఏవి?
సాధన.
కృష్ణ = 41 కి.గ్రా. – అత్యధిక బరువు
శ్రీకరి = 35 కి.గ్రా. – అత్యల్ప బరువు

ప్రశ్న 2.
సేకరించిన దత్తాంశమునకు అంకగణిత సగటు కనుగొనుము.
సాధన.
ఇవ్వబడిన రాశులు: 38, 39, 40, 36, 35, 37, 36, 41, 39, 39.
రాశుల మొత్తం = 38 + 39 + 40 + 36 + 35 + 37 + 36 + 41 + 39 + 39 = 380
రాశుల సంఖ్య = 10
రాశుల మొత్తము 38 అంకగణిత సగటు = రాశుల సంబం – 10 = 38 కి.గ్రా.

ప్రశ్న 3.
అంకగణిత సగటు, అత్యధిక మరియు అత్యల్ప పరిశీలనా విలువల మధ్య ఉన్నదో లేదో గమనించండి.
సాధన.
అంకగణిత సగటు 38 కి.గ్రా. అత్యధిక బరువు 41 కి.గ్రా. మరియు అత్యల్ప బరువు 35 కి.గ్రా. మధ్య ఉన్నది.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 220]

ప్రశ్న 1.
మొదటి 10 పూర్ణాంకముల వ్యాప్తి కనుగొనుము.
సాధన.
మొదటి 10 పూర్ణాంకాలు : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
వ్యాప్తి = గరిష్ఠ విలువ – కనిష్ఠ విలువ
= 9 – 0 = 9
∴ మొదటి 10 పూర్ణాంకాల వ్యాప్తి = 9.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 222]

10, 9, 12, 10, 8, 7, 6, 10, 9, 7, 8, 5 మరియు 2 రాశుల బాహుళకము ఎంత ?
సాధన.
ఇచ్చిన దత్తాంశాన్ని ఒక క్రమపద్ధతిలో అమర్చగా
2, 5, 6, 7, 7, 8, 8, 9, 9, 10, 10, 10, 12
మిగతా రాశుల కన్నా 10 ఎక్కువసార్లు పునరావృతం అయినది.
∴ బాహుళకం = 10

అన్వేషిద్దాం [పేజి నెం. 222]

ఒక పాచికను తీసుకోండి. దానిని 20 సార్లు దొర్లించండి. పాచిక పై భాగంలో వచ్చిన అంకెలను నమోదు చేయండి. ఆ అంకెల బాహుళకం కనుగొనుము.

సాధన.
ఒక పాచికను 20 సార్లు దొర్లించగా వచ్చిన అంకెలు
2, 4, 5, 3, 1, 6, 5, 4, 2, 1, 3, 5, 4, 2, 6, 2, 2, 5, 1, 3.
ఇచ్చిన రాశులలో ఒకే విధమైన రాశులను ఒక క్రమ పద్ధతిలో అమర్చితే
1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6.
మిగతా వాటికంటే ‘2’ ఎక్కువసార్లు పునరావృతం అయింది.
∴ బాహుళకం = 2.

ఆలోచించండి [పేజి నెం. 222]

కింది పట్టికలో విద్యార్థులు. రోజుకు చదువులో వెచ్చించే సమయం (గంటలలో) ఇవ్వబడినది అయిన బాహుళకము కనుగొనుము.

సాధన.
ఎక్కువ మంది విద్యార్థులు 1 గంట సమయం చదువుటలో వెచ్చించడం జరిగినది.
కావున, ఇచ్చిన దత్తాంశం యొక్క బాహుళకం = 4.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 228]

మొదటి 7 ప్రధాన సంఖ్యల మధ్యగతము కనుగొనుము.
సాధన.
మొదటి 7 ప్రధాన సంఖ్యలు 2, 3, 5, 7, 11, 13, 17.
7 రాశులలో \(\left(\frac{7+1}{2}=\frac{8}{2}=4\right)\) 4వ రాశి మధ్యగతము.
∴ మధ్యగతము = 7.

అన్వేషిదాం [పేజి నెం. 228]

మీ పాఠశాల లేదా మీకు సమీపంలో గల పాఠశాల యొక్క గత 6 సంవత్సరాల పదవ తరగతి ఉత్తీర్ణతా శాతములను నమోదు చేసి మధ్యగతము కనుగొనుము.
సాధన.
మా పాఠశాల యొక్క గత 6 సంవత్సరాల పదవ తరగతి ఉత్తీర్ణతా శాతములు :
100%, 98%, 93%, 95%, 96%, 97%.
ఇవ్వబడిన పరిశీలనలను ఆరోహణ క్రమంలో అమర్చగా,

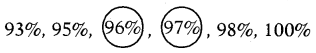
ఈ ఆరు పరిశీలనలలో 3 మరియు 4 పరిశీలనలు 96% మరియు 97%.
ఇక్కడ, 96% మరియు 97% అనునవి రెండు ముఖ్య మధ్యమ విలువలు.
మధ్యగతము = రెండు ముఖ్య మధ్యమ విలువల సగటు
= \(\frac{96+97}{2}\) = 96.5%
∴ దత్తాంశము యొక్క మధ్యగతము = 96.5%

ప్రాజెక్టు పని [పేజి నెం. 228]

మీ తల్లి తండ్రితో పాటు దగ్గరలోని కూరగాయల మార్కెట్ ను సందర్శించి, వివిధ కూరగాయల ధరలు సేకరించండి. క్రింది పట్టికను పూరించి, కేంద్రీయ స్థాన విలువలు కనుగొనుము.

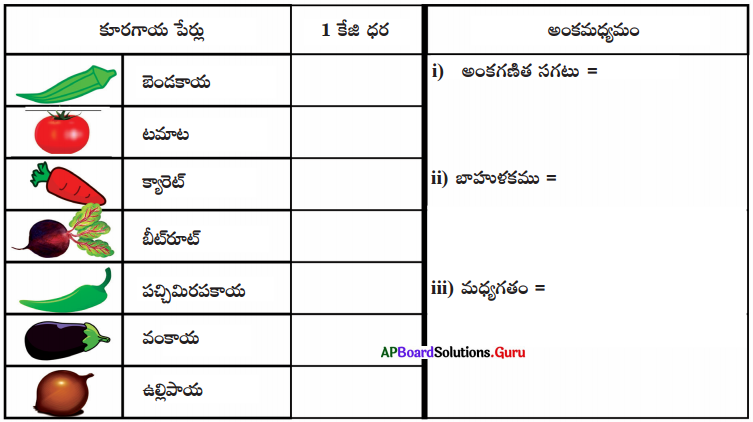
సాధన.

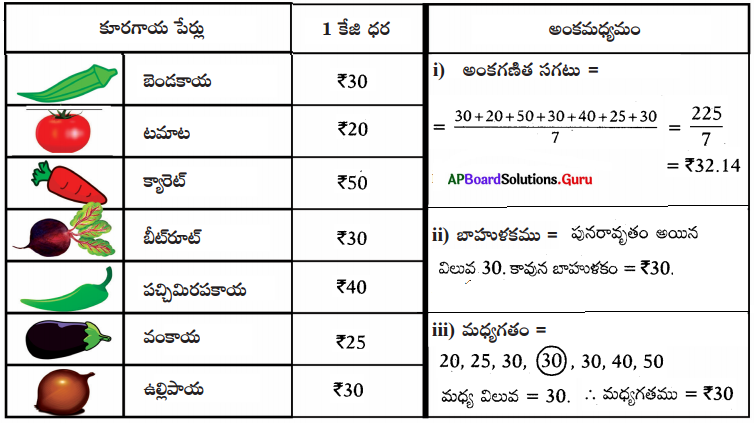
[పేజి నెం. 230]

ప్రసన్న ఒక మొబైల్ ఫోన్ కొనాలనుకున్నాడు. అతను ఒకే లక్షణాలు (సౌకర్యాలు) గల రెండు విభిన్న కంపెనీల మొబైల్ ఫోన్లను ఎంపిక చేసుకున్నాడు. ఈ రెండు మొబైల్ ఫోనుల్లో ఏది మెరుగైనదో అతను తెలుసుకోవాలనుకున్నాడు. అతను వివిధ పత్రికలు మరియు మ్యాగజైన్లు నుండి ఈ క్రింది సమాచారమును సేకరించాడు.

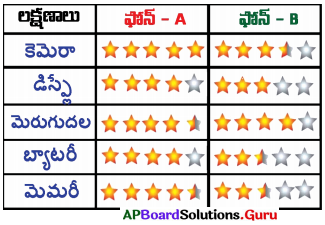
ప్రశ్న 1.
ప్రక్క పట్టికలో గల సమాచారం దేనిని సూచిస్తుంది ?
జవాబు
ప్రక్క పట్టిక మొబైల్ ఫోన్ల గురించి సమాచారం సూచిస్తుంది.

ప్రశ్న 2.
పట్టికలోని సమాచారం ప్రసన్నకు ఉపయోగపడుతుందా ?
జవాబు
అవును.

ప్రశ్న 3.
నీవైతే ప్రసన్నకు, ఏ మొబైల్ ఫోన్ ను సూచిస్తావు ?
జవాబు
ఫోన్ – A. (21 + \(\frac{1}{2}\) + \(\frac{1}{2}\) రేటింగ్)

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 232]

ప్రక్క కమ్మీ చిత్రంను గమనించి, కింది ప్రశ్నలకు సమాధానాలు రాయుము.

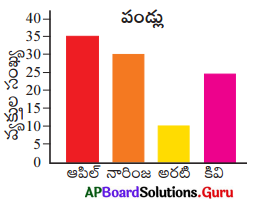
ప్రశ్న 1.
ఎక్కువ మంది ఇష్టపడే పండు ఏది ?
జవాబు
ఆపిల్.

ప్రశ్న 2.
అరటి పండును ఇష్టపడే వారి సంఖ్య ఎంత ?
జవాబు
10.

[పేజి నెం. 232]

ప్రక్కనున్న చిత్రాన్ని గమనించండి. ఇవ్వబడిన రెండు వరుసల కమ్మీ చిత్రంను పరిశీలించి, క్రింది ప్రశ్నలకు సమాధానాలు రాయండి.

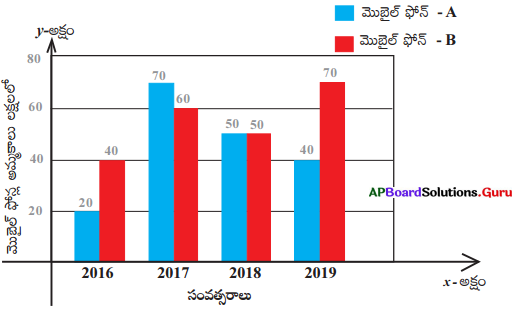
ప్రశ్న 1.
ఏ సంవత్సరములో రెండు మొబైల్ ఫోన్ కంపెనీల అమ్మకాలు సమానం ?
జవాబు
2018.

ప్రశ్న 2.
2017 వ సంవత్సరములో ఏ మొబైల్ ఫోన్ కంపెనీ అమ్మకాలు ఎక్కువ ?
జవాబు
మొబైల్ ఫోన్ – A.

[పేజి నెం. 236]

ప్రశ్న 1.
ప్రక్క పటంను గమనించండి.

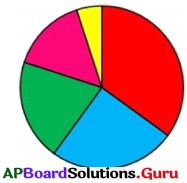
(1) వృత్తములోని అధిక భాగము ఏ రంగుతో షేడ్ చేయబడినది ?
జవాబు
ఎరుపు రంగు.

(2) నీలం రంగు, పింక్ రంగు భాగాలు సమాన పరిమాణములో ఉన్నాయా ?
జవాబు
లేవు.

(3) వృత్తములోని అత్యల్ప భాగము ఏ రంగుతో షేడ్ చేయబడినది ?
జవాబు
పసుపు రంగు.

ప్రశ్న 2.
కింది పటములో మానస కుటుంబం యొక్క వివిధ ఖర్చుల వివరాలు చూపబడ్డాయి.

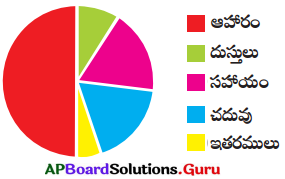
(i) అధిక భాగం దేని కొరకు ఖర్చు పెట్టబడింది ?
జవాబు
ఆహారం.

(ii) సమాన మొత్తంలో ఖర్చు చేయబడిన అంశాలు ఏవి ?
జవాబు
సహాయం మరియు చదువు.

(iii) అత్యల్ప భాగం దేని కొరకు ఖర్చు పెట్టబడింది ?
జవాబు
ఇతరములు.

ప్రాజెక్టు పని [పేజి నెం. 244]

మ్యాగజైన్లు, దినపత్రికలలో కమ్మీ చిత్రాలు, పై చిత్రాల రూపంలో ఉన్న సమాచారాన్ని సేకరించండి. మీ తరగతి గోడపత్రికపై ప్రదర్శించండి.
సాధన.
విద్యార్థులు సొంతంగా నిర్వహించాలి.

తార్కిక విభాగం అక్షర శ్రేణి [పేజి నెం. 246]

అక్షరశ్రేణి అనేది ఒక నిర్దిష్ట క్రమంలో అమర్చబడ్డ ఇంగ్లీష్ అక్షరమాల యొక్క తార్కిక అమరిక. వీటిలో అక్షరాలశ్రేణి .. (అక్షరాలు), అక్షరాల సమూహాలు లేదా అక్షరాలు మరియు సంఖ్యల కలయిక ఇవ్వబడింది. ప్రతి అక్షరం లేదా అక్షరాల సమూహంను పదం అని అంటారు. శ్రేణిలోని పదాలు ఒక నిర్దిష్ట క్రమంలో లేదా నమూనాలో అమర్చబడ్డాయి. మనం శ్రేణిని గుర్తించి ఖాళీలో, ఆ శ్రేణిని సంతృప్తి పరచే పదము (తరువాత పదం) ఆ ప్రత్యామ్నాయాల నుండి కనుగొనాలి. అక్షరాల శ్రేణిని సాధన చేయడానికి అక్షరాలకు నెంబర్లు కేటాయించడం ఎంతో ఉపయోగకరంగా ఉంటుంది.

ఉదాహరణలు:
ప్రశ్న 1.
B, D, E, H, …………
(1) 1
(2) K
(3) J
(4) L
జవాబు
(3) J

వివరణ:

ప్రశ్న 2.
A, B, D, E, G, ………….
(1) H
(2) I
(3) K
(4)F
జవాబు
(1) H

వివరణ:

ప్రశ్న 3.
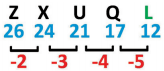
Z, X, U, Q, ………….
(1) M
(2) K
( 3) N
(4) L
జవాబు
(4) L

వివరణ:

ప్రశ్న 4.
QPO, NML, KJI, ……… EDC
(1) KL
(2) GHI
(3) CAB
(4) HGF
జవాబు
ఇచ్చిన శ్రేణిలోని అక్షరాలు ఇంగ్లీష్ అక్షరమాల యొక్క వ్యతిరేక (అపసవ్య) దిశ రాయబడ్డాయి కాబట్టి జవాబు ‘HGF’ అగును.

ప్రశ్న 5.
AB, DE, HI, MN, ………..
(1) TV
(2) TU
(3) ST
(4) RS
జవాబు
(3) ST

వివరణ:

కాబట్టి, శ్రేణిలోని తరువాత వచ్చే పదం ‘ST’.

ప్రశ్న 6.
AB, EF, IJ, MN, ………….
(1) QR
(2) OP
(3) XY
(4) PQ
జవాబు
(1) QR

వివరణ:

కాబట్టి, శ్రేణిలోని తరువాత వచ్చే పదం ‘QR’

ప్రశ్న 7.
B2, D4, F6, H8, J10, ………
(1) L12
(2) K11
(3) N14
(4) M13
జవాబు
(1) L12

వివరణ:
అక్షరాలు మరియు వాటికి కేటాయించిన సంఖ్యలు (ఒకటి విడిచి ఒకటి) కాబట్టి, జవాబు ‘L12’.

ప్రశ్న 8.
AFK, BGL, CHM, DIN, ……… .
(1) GJO
(2) FIO
(3) EJO
(4) GUN
జవాబు
(3) EJO

వివరణ:
ప్రతీ సమూహంలో అక్షరం మరియు దాని తరువాత వచ్చే యొక్క 5 వ అక్షరం కాబట్టి జవాబు ‘EJO’.

ఉదాహరణ

ప్రశ్న 1.
ఒక పాఠశాలలో మధ్యాహ్న భోజన పథకములో 6 రోజులపాటు భుజించిన విద్యార్థుల సంఖ్య వరుసగా 132, 164, 145, 182, 163 మరియు 114 అయిన మధ్యాహ్నం భోజనం చేసిన విద్యార్థుల అంకగణిత సగటు కనుగొనుము.
సాధన.
మధ్యాహ్న భోజన పథకములో 6 రోజులపాటు భుజించిన విద్యార్థుల సంఖ్య వరుసగా 132, 164, 145, 182, 163, 114.

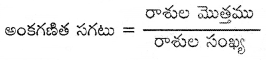
= \(\frac{132+164+145+182+163+114}{6}\) = \(\frac{900}{6}\) = 150

ప్రశ్న 2.
విద్యార్థుల వయసులు (సంవత్సరాలలో) 8, 5, 6, 6, 5, 7, 5, 6, 5, 4, 7, 6, 7, 6, 5, 8 మరియు 6 అయిన వాటి బాహుళకము ఎంత ?
సాధన.
విద్యార్థుల వయసులు 8, 5, 6, 6, 5, 7, 5, 6, 5, 4, 7, 6, 7, 6, 5, 8, 6 గా ఇవ్వబడినవి.
ఇచ్చిన రాశులలో ఒకే విలువ గల రాశులను ఒక క్రమ పద్ధతిలో అమర్చితే
4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 8, 8.
మిగతా వాటికంటే ‘6’ ఎక్కువసార్లు పునరావృతం అయినది.
∴ కాబట్టి బాహుళకము = 6

ప్రశ్న 3.
A, B, E, A, C, E, B, C, D, A, D, C, E, A మరియు C యొక్క బాహుళకం ఎంత ?
సాధన.
A, B, E, A, C, E, B, C, D, A, D, C, E, A, C లు ఇవ్వబడ్డాయి.
ఇచ్చిన రాశులలో ఒకే విధమైన రాశులను ఒక క్రమ పద్ధతిలో అమర్చితే,
A, A, A, A, B, B, C, C, C, C, D, D, E, E, F
మిగతా వాటికంటే ‘A’ మరియు ‘C’ లు ఎక్కువ సార్లు పునరావృతం అయ్యాయి.
∴ కాబట్టి బాహుళకము = ‘A’ మరియు ‘C’

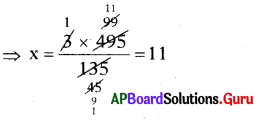
ప్రశ్న 4.
32, 43, 25, 67, 46, 71 మరియు 182 ల మధ్యగతము కనుగొనుము.
సాధన.
32, 43, 25, 67, 46, 71, 182
ఇచ్చిన రాశులు ఆరోహణ క్రమములో అమర్చిలే

దత్తాంశములోని ఏడు రాశులలో 4వ రాశి మధ్యపదం అగును.
∴ మధ్యగతము = 46.

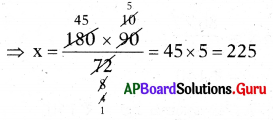
ప్రశ్న 5.
8 మంది నెలసరి ఆదాయాలు ₹8000, ₹9000, ₹8200, ₹7900, ₹8500, ₹8600, ₹7700 మరియు ₹60000 అయిన వారి మధ్యగత ఆదాయాన్ని కనుగొనుము.
సాధన.
8 కుటుంబాల నెలసరి ఆదాయాలు
₹8000, ₹9000, ₹8200, ₹7900, ₹8500, ₹8600, ₹7700, ₹60000
ఆదాయాలను ఆరోహణ క్రమములో అమర్చితే,

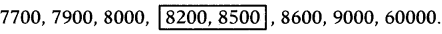
మధ్యమ పదాలు 8200 మరియు 8500.
మధ్యగతం, 8200, 8500 ల సరాసరి అగును.
∴ మధ్యగతం = \(\frac{8200+8500}{2}\) = \(\frac{16700}{2}\) = ₹18,350

ప్రశ్న 6.
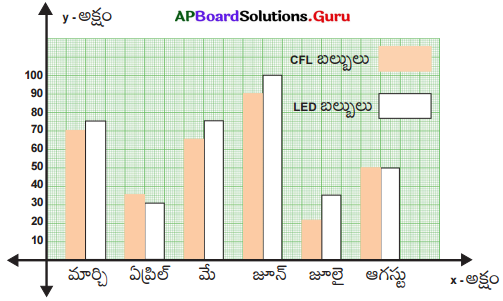
ఒక దుకాణదారుడు మార్చి నుండి ఆగష్టు వరకు ప్రతీ నెలలో అమ్మిన CFL బల్బులు మరియు LED బల్బుల అమ్మకాల వివరాలు క్రింది పట్టికలో ఇవ్వబడ్డాయి అయిన క్రింది దత్తాంశమునకు రెండు వరుసల కమ్మీ చిత్రాన్ని నిర్మించండి.

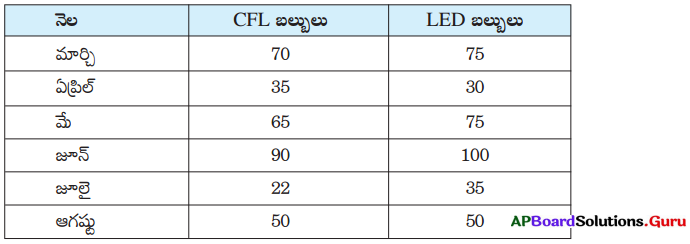
సాధన.
రెండు వరుసల కమ్మీ చిత్రం నిర్మాణములో సోపానాలు :

1. గ్రాఫు కాగితముపై X – అక్షం (క్షితిజ రేఖ), Y – అక్షం (నిలువు రేఖ) గీయండి. వాటి ఖండన బిందువును ‘O’ గా గుర్తించండి.
2. X – అక్షంపై నెలల పేర్లు తీసుకోండి.
3. Y – అక్షంపై CFL బల్బుల సంఖ్య, LED బల్బుల సంఖ్యను తీసుకోండి.
4. రెండు రకాల బల్బుల సంఖ్య గ్రాఫ్ కాగితముపై గుర్తించుటకు వీలుగా సరైన స్కేలును Y – అక్షంపై తీసుకోండి.
   Y – అక్షంపై గుర్తించవలసిన గరిష్ఠ విలువ 100. కాబట్టి 1 సెం.మీ. = 10 బల్బులుగా తీసుకోవచ్చు.
5. ఇచ్చిన విలువలను 10తో భాగించుట ద్వారా కమ్మీ పొడవు నిర్ధారించండి. (సూచిక భిన్నం 1 సెం.మీ. = 10 బల్బులు).
   ఉదా: 70 CFL బల్బులను సూచించు కమ్మీ పొడవు = \(\frac{70}{10}\) = 7 సెం.మీ.
   75 LED బల్బులను సూచించు కమ్మీ పొడవు = \(\frac{70}{10}\) = 7.5 సెం.మీ.
6. ప్రతీ నెలలో అమ్మిన CFL బల్బులు మరియు LED బల్బుల సంఖ్యను సమాన వెడల్పు గల కమ్మీల రూపములో ప్రక్క ప్రక్కన గీయండి.

ప్రశ్న 7.
ఒక పాఠశాలలోని 7వ తరగతిలో 100 మంది విద్యార్థులు కలరు. 7వ తరగతిలోని ప్రతీ విద్యార్థి ఏదో ఒక క్లబ్ లో సభ్యులుగా ఉన్నారు. కింది పట్టిక వివిధ క్లబ్ లోని విద్యార్థుల సంఖ్యను చూపుతుంది. అయిన పట్టికలోని సమాచారానికి పై చిత్రాన్ని గీయండి.

సాధన.
సెక్టారు యొక్క కోణం క్లబ్ లోని విద్యార్థుల సంఖ్య మరియు మొత్తం విద్యార్థుల సంఖ్యకు గల నిష్పత్తిపై ఆధారపడును.

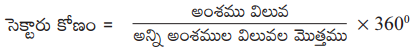
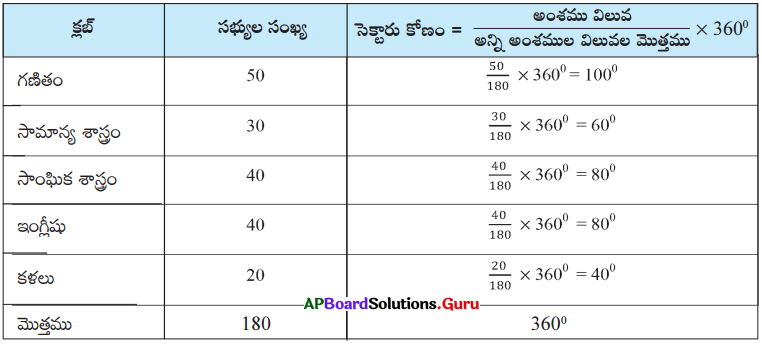
నిర్మాణ సోపానాలు:

1. ఏదేని వ్యాసార్థంతో వృత్తాన్ని గీచి, దాని కేంద్రాన్ని ‘O’ గా గుర్తించండి.
2. వృత్త పరిధిపై ఏదైనా ఒక బిందువును ‘A’ గా గుర్తించండి. OA ను కలపండి.
3. గణిత క్లబ్ ‘సెక్టారును సూచించునట్లు ∠AOB = 100°ని నిర్మించండి.
4. సామాన్య శాస్త్రం క్లబ్ సెక్టారును సూచించునట్లు ∠BOC = 60°ని నిర్మించండి.
5. సాంఘిక శాస్త్రం క్లబ్ సెక్టారును సూచించునట్లు ∠COD = 80° ని నిర్మించండి.
6. ఇంగ్లీషు క్లబ్ సెక్టారును సూచించునట్లు ∠DOE = 80°ని నిర్మించండి.
7. ∠EOA = 40° అనే సెక్టారు కోణం కళల క్లబ్ ను సూచిస్తుంది.

సాధనా ప్రశ్నలు [పేజి నెం. 248]

దిగువ అక్షరశ్రేణిలో, ఖాళీలలో ఉండవలసిన పదం (తరువాత పదం) ను ఇచ్చిన ఐచ్ఛికాల నుండి ఎంచుకొని పూరించండి.

ప్రశ్న 1.
B, F, J, N, R, V, …..
(a) Z
(b) W
(c) X
(d) Y
జవాబు
(a) Z

వివరణ:

ప్రశ్న 2.
A, C, E, G, I, K, ………
(a) P
(b) O
(c) N
(d) M
జవాబు
(d) M

వివరణ:

ప్రశ్న 3.
M, O, R, T, ……..
(a) W
(b) U
(c) V
(d) Q
జవాబు
(a) W

వివరణ:

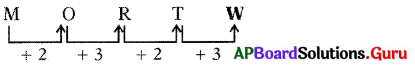
ప్రశ్న 4.
U, S, P, L, ……….
(a) F
(b) G
(c) H
(d) I
జవాబు
(b) G

వివరణ:

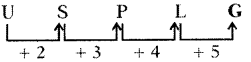
ప్రశ్న 5.
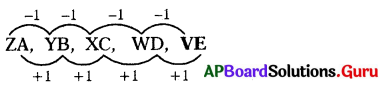
ZA, YB, XC, WD, …..
(a) UE
(b) EV
(c) VE
(d) SH
జవాబు
(c) VE

వివరణ:

ప్రశ్న 6.
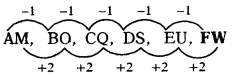
AM, BO, CQ, DS, EU, …..
(a) WF
(b) FU
(c) GV
(d) KJ
జవాబు
(d) KJ

వివరణ:

ప్రశ్న 7.
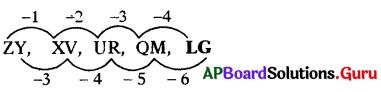
ZY, XV, UR, QM, …….
(a) LG
(b) LI
(c) LH
(d) KJ
జవాబు
(a) LG

వివరణ:

ప్రశ్న 8.
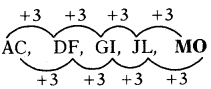
AC, DF, GI, JL, …..
(a) NO
(b) MO
(c) MN
(d) NP
జవాబు
(b) MO

వివరణ:

ప్రశ్న 9.
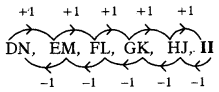
DN, EM, FL, GK, HJ, …..
(a) IK
(b) GI
(c) IJ
(d) NP
జవాబు
(d) NP

వివరణ:

ప్రశ్న 10.
CBA, STU, FED, VWX, …..
(a) IHG
(b) GHI
(c) IJK
(d) YZA
జవాబు
(a) IHG

వివరణ:

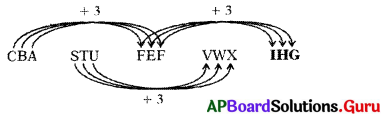
ప్రశ్న 11.
AZC, DYF, GXI, JWL, …..
(a) OVM
(b) UNV
(c) MVO
(d) MNO
జవాబు
(c) MVO

వివరణ:

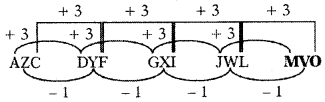
ప్రశ్న 12.
ABK, CDL, EFM, GHN, …..
(a) JIO
(b) IJO
(c)MNO
(d) ONM
జవాబు
(b) IJO

వివరణ:

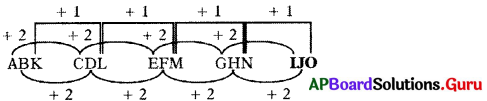
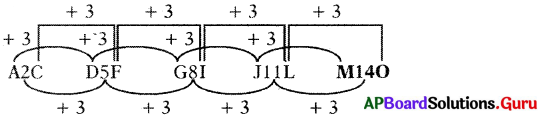
ప్రశ్న 13.
A2C, D5F, GRI, J11L, ………
(a) M140
(b) M120
(c) N15P
(d) N12P
జవాబు
(a) M140

వివరణ:

ప్రశ్న 14.
A, CD, HIJ, PORS, …..
(a) ZABCD
(b) ZYXW
(c) ABCDE
(d) RSTUV
జవాబు
(c) ABCDE

వివరణ:

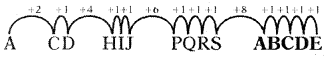
ప్రతి పదానికి ఒక అక్షరం పెరుగుతున్నది. కావున, సమాధానంలో 5 అక్షరాలుండాలి.

ప్రశ్న 15.
A, BC, DEF, GHIJ, …..
(a) KLMNP
(b) LMNOP
(c) KLMNO
(d) JKLMN
జవాబు
(c) KLMNO

వివరణ:

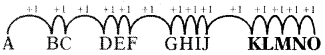
ప్రతి పదానికి ఒక్కొక్క అక్షరం పెరుగుతున్నది. కావున, సమాధానంలో 5 అక్షరాలుండాలి.

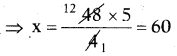
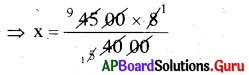
SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు InText Questions

[పేజి నెం. 17]

ఇప్పుడు ఇచ్చిన సంఖ్యలకు పూర్వ సంఖ్య, ఉత్తర సంఖ్యలతో కింది పట్టికను పూరించండి.

సాధన.

చర్చించండి [పేజి నెం. 17]

ప్రశ్న 1.
ఏ సహజ సంఖ్యకు ఉత్తర సంఖ్య లేదు?
సాధన.
ప్రతి పూర్ణాంకానికి ఉత్తర సంఖ్య ఉంది.

ప్రశ్న 2.
ఏ సహజ సంఖ్యకు పూర్వ సంఖ్య లేదు ?
సాధన.
పూర్ణాంకాలన్నింటిలో ‘0’ (సున్నా)కి పూర్వ సంఖ్య లేదు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 18]

కనిష్ఠ పూర్ణాంకమేది?
సాధన.
కనిష్ఠ పూర్ణాంకము ‘0’.

ఆలోచించండి [పేజి నెం. 18]

ప్రశ్న 1.
సహజ సంఖ్యలన్నీ పూర్ణాంకాలు అవుతాయా?
సాధన.
సహజ సంఖ్యలు అన్నీ పూర్ణాంకాలు అవుతాయి.

ప్రశ్న 2.
పూర్ణాంకాలన్నీ సహజసంఖ్యలు అవుతాయా?
సాధన.
పూర్ణాంకాలన్నీ సహజసంఖ్యలు కావు. ‘0’ పూర్ణాంకము.
కాని సహజ సంఖ్య కాదు. అనగా ‘0’ తప్ప మిగిలిన అన్ని పూర్ణాంకాలు సహజ సంఖ్యలు అవుతాయి.

ఇవి చేయండి [పేజి నెం. 19]

కింది వాటిని సంఖ్యారేఖపై సూచించండి.
అ) 5 + 3
సాదన.

ఆ) 5 – 3
సాధన.

ఇ) 3 + 5
సాదన.

ఈ) 10 + 1
సాదన.

ఉ) 8 – 5
సాధన.

ప్రయత్నించండి [పేజి నెం. 19]

సంఖ్యారేఖను ఉపయోగించి కింది వాటిని కనుగొనండి.
ప్రశ్న 1.
5 రావాలంటే 8 నుండి ఏ సంఖ్యను తీసివేయాలి?
సాధన.

ప్రశ్న 2.
1 రావాలంటే 6 నుండి ఏ సంఖ్యను తీసివేయాలి?
సాధన.

ప్రశ్న 3.
8 రావాలంటే 6 కి ఏ సంఖ్యను కలపాలి?
సాధన.

ప్రశ్న 4.
30 రావాలంటే ఎన్ని 6 లు అవసరం?
సాధన.

రాజు, గాయత్రిలు కలిసి సంఖ్యారేఖను తయారుచేసి దానిపై ఒక ఆట ఆడుతున్నారు.

సంఖ్యారేఖపై సున్న వద్ద ప్రారంభించి మొదటిసారి 3 ప్రమాణాలు, రెండవసారి 8 ప్రమాణాలు, మూడవసారి 5 ప్రమాణాల చొప్పున దూకితే నీవు చివరకు సంఖ్యారేఖపై ఎక్కడికి చేరుకుంటావు అని గాయత్రిని రాజు అడిగాడు. మొదటిసారి 3ని, రెండవసారి 11ని, చివరగా 16ని చేరుకుంటానని గాయత్రి సమాధానం చెప్పింది.
గాయత్రి సమాధానం సరియైనదని నీవు భావిస్తున్నావా ? గాయత్రి మార్గంను సంఖ్యారేఖపై సూచించండి.
సంకలన, వ్యవకలనాల ఆధారంగా ఈ ఆటను నీ మిత్రునితో కలిసి ఆడుము.
సాధన.
అవును. గాయత్రి సమాధానం సరియైనది.

ఆలోచించండి [పేజి నెం. 21]

ప్రశ్న 1.
పూర్ణాంకాల సమితి వ్యవకలనంలో సంవృత ధర్మాన్ని పాటిస్తుందా?
సాధన.
8, 5 లు పూర్ణాంకాలు. 8 – 5 = 3 ఒక పూర్ణాంకము.
5 – 8 = -3 పూర్ణాంకము కాదు.
కావున పూర్ణాంకాల సమితి వ్యవకలనంలో సంవృత ధర్మాన్ని పాటించదు.

ప్రశ్న 2.
పూర్ణాంకాల సమితి భాగహారంలో సంవృత ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 3 లు రెండు పూర్ణాంకాలు.
6 ÷ 3 = 2 ఒక పూర్ణాంకము
3 ÷ 6 = \(\frac {3}{6}\) పూర్ణాంకం కాదు.
కావున, పూర్ణాంకాల సమితి భాగహారంలో సంవృత ధర్మాన్ని పాటించదు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 21]

ప్రశ్న 1.
12 ÷ 3 మరియు 42 ÷ 7 లను కనుగొనండి.
సాధన.
12 ÷ 3
12 – 3 = 9 → 1వ సారి
9 – 3 = 6 → 2వ సారి
6 – 3 = 3 → 3వ సారి
3 – 3 = 0 → 4వ సారి
12 ÷ 3 = 4

42 ÷ 7
42 – 7 = 35 → 1వ సారి
35 – 7 = 28 → 2వ సారి
28 – 7 = 21 → 3వ సారి
21 – 7 = 14 → 4వ సారి
14 – 7 = 7 → 5వ సారి
7 – 7 = 0 → 6వ సారి
కావున 42 ÷ 7 = 6

ప్రశ్న 2.
6 ÷ 0 మరియు 9 ÷ 0 సమానాలు అవుతాయా?
సాధన.
0 తో భాగహారం నిర్వచించబడదు. కావున 6 ÷ 0 మరియు 9 ÷ 0 సమానం అవుతాయని చెప్పలేము.

ప్రయత్నించండి [పేజి నెం. 22]

పూర్ణాంకాల సమితి వ్యవకలనం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 4 లు రెండు పూర్ణాంకాలు.
6 – 4 = 2 మరియు 4 – 6 = -2 పూర్ణాంకము కాదు.
కావున 6 – 4 ≠ 4 – 6
పూర్ణాంకాల సమితి వ్యవకలనం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించదు.

పూర్ణాంకాల సమితి భాగహారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 4 లు రెండు పూర్ణాంకాలు
6 ÷ 4 = \(\frac{6}{4}=\frac{3}{2}\) మరియు 4 ÷ 6 = \(\frac {2}{3}\) పూర్ణాంకము కాదు.
కావున 6 ÷ 4 ≠ 4 ÷ 6
కావున పూర్ణాంకాల సమితి భాగహారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించదు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 23]

సరిచూడండి.
i) (5 × 6) × 2 = 5 × (6 × 2)
సాధన.
ఎడమచేతివైపు (L.H.S) = (5 × 6) × 2
= 30 × 2 = 60
కుడిచేతివైపు (R.H.S) = 5 × (6 × 2)
= 5 × 12 = 60
∴ L.H.S = R.H.S
కావున (5 × 6) × 2 = 5 × (6 × 2) సరైనదే.

ii) (3 × 7) × 5= 3 × (7 × 5)
సాధన.
ఎడమచేతివైపు (L.H.S) = (3 × 7) × 5
= 21 × 5 = 105
కుడిచేతివైపు (R.H.S) = 3 × (7 × 5)
= 3 × 35 = 105
∴ L.H.S = R.H.S
కావున (3 × 7) × 5 = 3 × (7 × 5) సరైనదే.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 24]

స్థిత్యంతర, సహచరధర్మాలను ఉపయోగించి కింది వాటిని సూక్ష్మీకరించండి.
అ) 319 + 69 +81
సాధన.
319 + 69 + 81 = 319 + (81 + 69) (స్థిత్యంతర ధర్మం )
= (319 +81) + 69 (సహచర ధర్మం )
= 400 + 69 = 469

ఆ) 431 + 37 + 69 + 63
సాధన.
431 + 37 + 69 + 63 = 431 + (37 + 69) + 63
= 431 + (69 + 37) + 63 (స్థిత్యంతర ధర్మం )
= (431 + 69) + (37 + 63) (సహచర ధర్మం )
= 500 + 100 = 600

ఇ) 2 × (71 × 5)
సాధన.
2 × (71 × 5) = 2 × (5 × 71) (స్థిత్యంతర ధర్మం )
= (2 × 5) × 71 (సహచర ధర్మం )
= 10 × 71 = 710

ఈ) 50 × 17 × 2
సాధన.
50 × (17 × 2) = 50 × (2 × 17) (స్థిత్యంతర ధర్మం)
= (50 × 2) × 17 (సహచర ధర్మం )
= 100 × 17 = 1700

ఆలోచించండి [పేజి నెం. 24]

(8 ÷ 2) ÷ 4 = 8 ÷ (2 ÷ 4) అవుతుందా ?
భాగహారానికి సహచరధర్మం వర్తిస్తుందా?
అలాగే వ్యవకలనానికి సహచరధర్మం వర్తిస్తుందేమో సరిచూడండి.
సాధన.
ఎడమచేతివైపు (L.H.S) = (8 ÷ 2) ÷ 4
= 4 ÷ 4 = 1
కుడిచేతివైపు (R.H.S) = 8 ÷ (2 ÷ 4)
= 8 ÷ (\(\frac {1}{2}\))
= 8 × 2 = 16
L.H.S ≠ R.H.S
కావున (8 ÷ 2) ÷ 4 = 8 ÷ (2 ÷ 4) కాదు.
అనగా భాగహారానికి సహచరధర్మం వర్తించదు.
ఇప్పుడు వ్యవకలనానికి సహచరధర్మం వర్తిస్తుందేమో ఒక ఉదాహరణతో పరిశీలిద్దాము.
(8 – 2) – 4 = 6 – 4 = 2
8 – (2 – 4) = 8 – (-2) = 8+ 2 = 10
∴ (8 – 2) – 4 ≠ 8 – (2 – 4)
కావున వ్యవకలనానికి సహచరధర్మం వర్తించదు.

[పేజి నెం. 24]

గుణకార విభాగ న్యాయం ఉపయోగించి కింది వాటిని సూక్ష్మీకరించండి.
అ) 2 × (5+ 6)
ఆ) 5 × (7 + 8)
ఇ) 19 × 7 + 19 × 3
సాధన.
అ) 2 × (5 + 6)
ఇచ్చినది 2 × (5 + 6) = (2 × 5) + (2 × 6)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
2 × 11 = 10 + 12
22 = 22
L.H.S. = R.H.S

ఆ) 5 × (7 + 8)
ఇచ్చినది 5 × (7 + 8) = (5 × 7) + (5 × 8)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
5 × 15 = 35 + 40
75 = 75
L.H.S : R.H.S

ఇ) 19 × 7 + 19 × 3
ఇచ్చినది (19 × 7) + (19 × 3) = 19 × (7 + 3)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
133 + 57 = 19 × 10
190 = 190
L.H.S = R.H.S

ఇవి చేయండి [పేజి.నెం. 24]

అ) 25 × 78 ఆ) 17 × 26 ఇ) 49 × 68 + 32 × 49 విభాగ న్యా యాన్ని ఉపయోగించి కనుగొనండి.
సాధన.
అ) 25 × 78
(20 + 5) × 78 = (20 × 78) + (5 × 78) (విభాగ న్యా యం )
= 1560 + 390 = 1950

ఆ) 17 × 26 = 17 × (20 + 6)
= (17 × 20) + (17 × 6) (విభాగ న్యాయం)
= 340 + 102 = 442

ఇ) 49 × 68 + 32 × 49
= 49 × (68 + 32) (విభాగ న్యాయం)
= 49 × 100 = 4900

[పేజి నెం. 26]

కింది పట్టికను పూరించండి.

సాధన.

ప్రయత్నించండి [పేజి నెం. 27]

ప్రశ్న 1.
ఏ సంఖ్యలను రేఖగా మాత్రమే చూపవచ్చు ?
సాధన.
2, 3, 4, 5, 6, 7, ………… సంఖ్యలను రేఖగా చూపవచ్చు.
2 గాని అంతకన్నా ఎక్కువగాని సంఖ్యలు కలిసి రేఖను ఏర్పరుస్తాయి.

ప్రశ్న 2.
ఏఏ సంఖ్యలను దీర్ఘచతురస్రాలుగా చూపవచ్చు?
సాధన.
6, 8, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, ……… సంఖ్యలను దీర్ఘచతురస్రాలుగా చూపవచ్చును.
పై సంఖ్యలన్నీ సంయుక్త సంఖ్యలని గమనించగలము.

ప్రశ్న 3.
ఏఏ సంఖ్యలను చతురస్రాలుగా చూపవచ్చు?
సాధన.
4, 9, 16, 25, ………. సంఖ్యలను చతురస్రాలుగా చూపవచ్చును.
పై సంఖ్యలను రెండు సమాన సంఖ్యల లబ్ధంగా రాయవచ్చును.
4 = 2 × 2
9 = 3 × 3
16 = 4 × 4
25 = 5 × 5
పై సంఖ్యలు 4, 9, 16, 25, ……….. లు పరిపూర్ణ వర్గ సంఖ్యలు.

ప్రశ్న 4.
ఏఏ సంఖ్యలమ త్రిభుజాలుగా చూపవచ్చు?
సాధన.
3, 6, 10, 15, 21, …………. సంఖ్యలను త్రిభుజాలుగా చూపవచ్చును.
పై సంఖ్యలను మొదటి వరుస సహజ సంఖ్యల మొత్తంగా రాయవచ్చును.
3 = 1 + 2
6 = 1 + 2 + 3
0 = 1 + 2 + 3 + 4
15 = 1 + 2 + 3 + 4 + 5
21 = 1 + 2 + 3 + 4 + 5 + 6
పై సంఖ్యలను 3, 6, 10, 15, 21, ……….. త్రిభుజ సంఖ్యలు అంటారు.

ఉదాహరణలు

ప్రశ్న 1.
196 + 57 + 4 కనుగొనండి.
సాధన.
196 + (57 + 4)
= 196 + (4 + 57) [స్థిత్యంతర ధర్మం]
= (196 + 4) + 57 [సహచర ధర్మం]
= 200 + 57 = 257

ప్రశ్న 2.
5 × 9 × 2 × 2 × 3 × 5 ని కనుగొనండి.
సాధన.
5 × 9 × 2 × 2 × 3 × 5
= 5 × 2 × 9 × 2 × 5 × 3 [స్థిత్యంతర ధర్మం]
= (5 × 2) × 9 × (2 × 5) × 3 [సహచర ధర్మం]
= 10 × 9 × 10 × 3
= 90 × 30 = 2700

ప్రశ్న 3.
12 × 75 విభాగన్యాయాన్ని ఉపయోగించి కనుక్కోండి.
సాధన.
12 × 75 = 12 × (70 + 5) = 12 × (80 – 5)
= (12 × 70) + (12 × 5) లేదా = (12 × 80) – (12 × 5)
= 840 + 60 = 900 = 960 – 60 = 900

SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు Unit Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు Unit Exercise

ప్రశ్న 1.
< లేదా > సరియైన గుర్తును ఎంపిక చేసుకొని కింది ఖాళీలను పూరించండి.
అ) 8 ……….. 7 ఆ) 5 ……….. 2 ఇ) 0 ………. 1 ఈ) 10 ………..5
సాధన.
అ) 8 …..>…… 7 ఆ) 5 ……>……2 ఇ) 0 ……<…… 1 ఈ) 10 ……>….. 5

ప్రశ్న 2.
11 యొక్క ఉత్తర సంఖ్య మరియు 5 యొక్క పూర్వ సంఖ్యలను సంఖ్యారేఖపై సూచించండి.
సాధన.
11 యొక్క ఉత్తర సంఖ్య = 12.
5 యొక్క పూర్వ సంఖ్య = 4.

ప్రశ్న 3.
కింది ప్రవచనాలలో ఏది సత్యమో, ఏది అసత్యమో కనుగొని అసత్య ప్రవచనాలను సరిచేసి రాయండి.
అ) పూర్వ సంఖ్యలేని ఒక సహజ సంఖ్య గలదు.
ఆ) ‘0’ అనునది కనిష్ఠ పూర్ణాంకం.
ఇ) సంఖ్యారేఖపై ఏదేని పూర్ణాంకమునకు ఎడమవైపు గల పూర్ణాంకము ఆ పూర్ణాంకము కంటే పెద్ద సంఖ్య.
సాధన.
అ)పూర్వ సంఖ్యలేని ఒక సహజ సంఖ్య గలదు. (సత్యం)
(పూర్వసంఖ్యలేని సహజసంఖ్య 1)
ఆ) ‘0’ అనునది కనిష్ఠ పూర్ణాంకం. (సత్యం )
ఇ) సంఖ్యారేఖ పై ఏదేని పూర్ణాంకమునకు ఎడమవైపు గల పూర్ణాంకము ఆ పూర్ణాంకము కంటే పెద్ద సంఖ్య. (అసత్యం)
సరిచేసి రాయగా:
సంఖ్యారేఖ పై ఏదేని పూర్ణాంకమునకు ఎడమవైపు గల పూర్ణాంకము ఆ పూర్ణాంకము కంటే చిన్న సంఖ్య.

ప్రశ్న 4.
ఇచ్చిన సమాచారం ఆధారంగా ఫలితాలను గణించకుండా చెప్పండి.
అ) 28 × 19 = 532 అయితే 19 × 28 =
ఆ) a × b = c అయితే b × a =
ఇ) 85 + 0 = 85 అయితే 0 + 85 =
సాధన.
అ) 28 × 19 = 532 అయితే 19 × 28 = 532
ఆ) a × b = అయితే b × a = c
ఇ) 85 + 0 = 85 అయితే 0 + 85 = 85

ప్రశ్న 5.
కింది వాటి విలువలను కనుగొనండి.
అ) 368 × 12 + 18 × 368
ఆ) 79 × 4319 + 4319 × 11
సాధన.
అ) 368 × 12 + 18 × 368 = 368 × (12 + 18) (విభాగ న్యా యం )
= 368 × 30 = 11040

ఆ) 79 × 4319 + 4319 × 11 = 4319 × (79 + 11) (విభాగ న్యాయం)
= 4319 × 90
= 388710

ప్రశ్న 6.
చందన, వేణులు వరుసగా 12 నోటు పుస్తకాలు, 10 నోటు పుస్తకాలను కొన్నారు. ఒక నోటు పుస్తకం ధర ₹ 15. అయితే దుకాణదారునికి ఎంత డబ్బు ఇవ్వాలి?
సాధన.
చందన కొన్న నోటు పుస్తకాలు = 12
వేణు కొన్న నోటు పుస్తకాలు = 10
ఒక్కొక్క నోటు పుస్తకం ధర = ₹15
దుకాణదారునికి ఇవ్వాల్సిన డబ్బు = (12 + 10) × 15
= 12 × 15 + 10 × 15
= 180 + 150
= ₹ 330

ప్రశ్న 7.
జతపరండి.

సాధన.
అ) iii,
ఆ) v,
ఇ) ii,
ఈ) i,
ఉ) iv

ప్రశ్న 8.
కింది అమరికను పరిశీలించండి.
91 × 11 × 1 = 1001
91 × 11 × 2 = 2002
91 × 11 × 3 = 3003
తర్వాత వచ్చే ఏడు సోపానాలు రాయండి. ఫలితం సరియైనదేమో సరి చూడండి.
సాధన.
91 × 11 × 4 = 4004
91 × 11 × 5 = 5005
91 × 11 × 6 = 6006
91 × 11 × 7 = 7007
91 × 11 × 8 = 8008
91 × 11 × 9 = 9009
91 × 11 × 10 = 10010

SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు Ex 2.3 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు Exercise 2.3

ప్రశ్న 1.
కింది అమరికను పరిశీలించండి.
1 × 8 + 1 = 9
12 × 8 + 2 = 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765
తర్వాత వచ్చే నాలుగు సోపానాలు రాయండి. ఈ అమరిక తర్వాత సంఖ్యలకు ఎలా వస్తుందో చెప్పగలరా?
సాధన.
తర్వాత వచ్చే నాలుగు సోపానాలు
123456 × 8 + 6 = 987654
1234567 × 8 + 7 = 9876543
12345678 × 8 + 8 = 98765432
123456789 × 8 + 9 = 987654321
L.H.S లో ఉన్న సంఖ్యల అమరిక పెరుగుతుంది. మరియు R.H.S లో ఉన్న ఫలితంలో కుడివైపున ఉన్న సంఖ్యలు తగ్గుతున్నాయి.

ప్రశ్న 2.
13680347, 35702369, 25692359 సంఖ్యలను 9తో గుణించి, ఎటువంటి అమరిక వస్తుందో పరిశీలించండి.
సాధన.
i) 13680347 × 9 = 13680347 × (10 – 1)
వ్యవకలనం మీద గుణకార విభాగన్యాయం ప్రకారం,
= 13680347 × 10 – 13680347 × 1
= 136803470 – 13680347
= 123123123

ii) 35702369 × 9 = 35702369 × (10 – 1)
వ్యవకలనం మీద గుణకార విభాగన్యాయం ప్రకారం,
= 35702369 × 10 – 35702369 × 1
= 357023690 – 35702369
= 321321321

iii) 25692359 × 9 = 25692359 × (10 – 1)
వ్యవకలనం మీద గుణకార విభాగన్యాయం ప్రకారం,
= 25692359 × 10 – 25692359 × 1
= 256923590 – 25692359
= 231231231

SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు Ex 2.2 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు Exercise 2.2

ప్రశ్న 1.
తగిన విధంగా సంఖ్యల స్థానాలు మార్చుకొని మొత్తాన్ని కనుగొనండి.
అ) 238 + 695 + 162
ఆ) 154 + 197 + 46 + 203
సాధన.
అ) 238 + 695 + 162 = 238 + 162 + 695 (స్థిత్యంతర ధర్మం )
= (238 + 162) + 695 (సహచర ధర్మం )
= 400 + 695 = 1095

ఆ) 154 + 197 + 46 + 203 = 154 + 46 + 197 + 203 (స్థిత్యంతర ధర్మం )
= (154 + 46) + (197 + 203) (సహచర ధర్మం)
= 200 + 400 = 600

ప్రశ్న 2.
తగిన విధంగా సంఖ్యల స్థానాలు మార్చుకొని లబ్దాన్ని కనుగొనండి.
అ) 25 × 1963 × 4
ఆ) 20 × 255 × 50 × 6
సాధన.
అ) 25 × 1963 × 4 = 25 × (4 × 1963) (స్థిత్యంతర ధర్మం)
= (25 × 4) × 1963 (సహచర ధర్మం)
= 100 × 1963 = 196300

ఆ) 20 × 255 × 50 × 6 = 20 × 50 × 255 × 6 (స్థిత్యంతర ధర్మం )
= (20 × 50) × (255 × 6) (సహచర ధర్మం)
= 1000 × 1530 = 15,30,000

ప్రశ్న 3.
తగిన ధర్మాలనుపయోగించి కింది లబ్దాలను కనుగొనండి.
అ) 205 × 1989
ఆ) 1991 × 1005
సాధన.
అ) 205 × 1989 = (200 + 5) × 1989
= (200 × 1989) + (5 × 1989) (విభాగన్యా యము)
= 397800 + 9945 = 407745

ఆ) 1991 × 1005 = 1991 × (1000 + 5)
= (1991 × 1000) + (1991 × 5) (విభాగ న్యాయము)
= 1991000 + 9955 = 2000955

ప్రశ్న 4.
ఒక పాల వ్యాపారి ఉదయం 56 లీటర్ల పాలను, సాయంత్రం 44 లీటర్ల పాలను ఒక వసతి గృహానికి సరఫరా చేస్తాడు. ఒక లీటరు పాల ధర ₹50 అయితే, అతనికి ఒక రోజుకు ఎంత డబ్బు వస్తుంది?
సాధన.

ఒక లీటరు పాల ధర = ₹50
∴ ఒక రోజుకు వచ్చు డబ్బు = 100 × 50 = ₹ 5000
(లేదా)
పాలవ్యాపారి ఉదయం సరఫరా చేసే పాలు = 56 లీ.
ఒక లీటరు పాలధర = ₹50
ఉదయం సరఫరా చేసే పాలకు వచ్చు డబ్బు = 56 × 50 ప
ాల వ్యాపారి సాయంత్రం సరఫరా చేసే పాలు = 44 లీ.
సాయంత్రం సరఫరా చేసే పాలకు వచ్చు డబ్బు = ₹ 44 × 50
∴ ఒక రోజుకు వచ్చు డబ్బు = 56 × 50 + 44 × 50
= (56 + 44) × 50
= 100 × 50
= ₹ 5000

SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు Ex 2.1 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు Exercise 2.1

ప్రశ్న 1.
27 మరియు 46 ల మధ్య ఎన్ని పూర్ణాంకాలుంటాయి?
సాధన.
27 మరియు 46 ల మధ్య గల పూర్ణాంకాలు
28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45.
27 మరియు 46 ల మధ్య 18 పూర్ణాంకాలు కలవు.
(లేదా) (46 – 27) – 1 = 19 – 1 = 18

ప్రశ్న 2.
సంఖ్యారేఖనుపయోగించి కింది వాటిని కనుగొనండి.
అ) 6 + 7 + 7 ఆ) 18 – 9 ఇ) 5 × 3
సాధన.
అ) 6 + 7 + 7

ఆ) 18 – 9

ఇ) 5 × 3

ప్రశ్న 3.
కింది జతలలో ఏ పూర్ణాంకం మరొక పూర్ణాంకానికి సంఖ్యారేఖపై కుడివైపున ఉంటుంది?
అ) 895, 239
సాధన.
895, 239 (895 > 239) కావున
895 సంఖ్యారేఖపై 239 కి కుడివైపున ఉంటుంది.

ఆ) 1001, 10001
సాధన.
1001, 10001 (10001 > 1001) కావున
10001 సంఖ్యారేఖ పై 1001 కి కుడివైపున ఉంటుంది.

ఇ) 15678, 4013
సాధన.
15678, 4013 (15678 > 4013) కావున
15678 సంఖ్యారేఖపై 4013 కు కుడివైపున ఉంటుంది.

ప్రశ్న 4.
కనిష్ఠ పూర్ణాంకాన్ని సంఖ్యారేఖపై చూపండి.
సాధన.
కనిష్ఠ పూర్ణాంకము ‘0’

SCERT AP 6th Class Maths Solutions Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 1st Lesson మన చుట్టూ ఉండే సంఖ్యలు InText Questions

[పేజి నెం. 6]

ఇవ్వబడిన సంఖ్యలను విస్తరణ రూపంలో రాద్దాం.

ప్రశ్న 1.
96,08,54,039
సాధన.
96,08,54,039 = 9 × 10,00,00,000 + 6 × 1,00,00,000 + 8 × 1,00,000 + 5 × 10,000 + 4 × 1,000 + 3 × 10 + 9 × 1
= తొంభైఆరు కోట్ల ఎనిమిది లక్షల యాభై నాలుగు వేల ముఫ్పై తొమ్మిది.

ప్రశ్న 2.
857,90,00,756
సాధన.
857,90,00,756 = 8 × 100,00,00,000 + 5 × 10,00,00,000 + 7 × 1,00,00,000 + 9 × 10,00,000 + 7 × 100 + 5 × 10+ 6 × 1
= ఎనిమిది వందల యాభై ఏడు కోట్ల తొంభై లక్షల ఏడు వందల యాభై ఆరు.

1 కోటి = 10 పది లక్షలు
= 100 లక్షలు
= 1000 పది వేలు
= 10,000 వేలు
= 1,00,000 వందలు
= 10,00,000 పదులు
= 1,00,00,000 ఒకట్లు

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 7]

పై పట్టికలో భాగంగా 10 కోట్లు మరియు 100 కోట్లను రాయండి.
సాధన.
10 కోట్లు : 100 పది లక్షలు
= 1000 లక్షలు
= 10,000 పది వేలు
= 1,00,000 వేలు
= 10,00,000 వందలు
= 1,00,00,000 పదులు
= 10,00,00,000 ఒకట్లు

100 కోట్లు = 10 పది కోట్లు
= 100 కోట్లు
= 1000 పది లక్షలు
= 1,00,000 పది వేలు
= 10,00,000 వేలు
= 1,00,00,000 వందలు
= 10,00,00,000 పదులు
= 100,00,00,000 ఒకట్లు

[పేజి నెం. 8]

అంతర్జాతీయ సంఖ్యామానం :

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 9]

ప్రశ్న 1.
పై పట్టికలోని మిగిలిన అంకెలను అంతర్జాతీయ సంఖ్యామానంలో అక్షరాలతో రాయండి.
సాధన.
896,800,705 : ఎనిమిది వందల తొంభై ఆరు మిలియన్ల ఎనిమిది వందల వేల ఏడు వందల ఐదు.
239,176,507,857 : రెండు వందల ముప్పై తొమ్మిది బిలియన్ల నూట డెబ్బై ఆరు మిలియన్ల ఐదు వందల ఏడు వేల ఎనిమిది వందల యాభై ఏడు.

ప్రశ్న 2.
మిగిలిన ఖాళీ పెట్టెలలో మీ సొంత అంకెలతో నింపి వాటిని అక్షరాలలో రాయండి.
సాధన.
9,490,275,276:
తొమ్మిది బిలియన్ల నాలుగు వందల తొంభై మిలియన్ల రెండు వందల డెబ్బై ఐదు వేల రెండు వందల డెబ్బై ఆరు.
85,559,793,120:
ఎనభై ఐదు బిలియన్ల ఐదు వందల యాభై తొమ్మిది మిలియన్ల ఏడు వందల తొంభై మూడు వేల నూట ఇరవై.
907,980,043,201:
తొమ్మిది వందల ఏడు బిలియన్ల తొమ్మిది వందల ఎనభై మిలియన్ల నలభై మూడు వేల రెండు వందల ఒకటి.

[పేజి నెం. 11]

1991, 2001, 2011 భారతదేశ జనాభా లెక్కల ప్రకారం జనాభా వివరాలు సేకరించి హిందూ సంఖ్యామానం, అంతర్జాతీయ సంఖ్యామానంలలోను అక్షరాలలో రాయండి.
సాధన.
1991 భారతదేశ జనాభా : 838583988
హిందూ సంఖ్యామానం : 83,85,83,988
ఎనభై మూడు కోట్ల ఎనభై ఐదు లక్షల ఎనభై మూడు వేల తొమ్మిది వందల ఎనభై ఎనిమిది.
అంతర్జాతీయ సంఖ్యామానం : 838,583,988
ఎనిమిది వందల ముప్పై ఎనిమిది మిలియన్ల ఐదు వందల ఎనభై మూడు వేల తొమ్మిది వందల ఎనభై ఎనిమిది.

2001 భారతదేశ జనాభా : 1028737436
హిందూ సంఖ్యామానం : 102,87,37,436
నూట రెండు కోట్ల ఎనభై ఏడు లక్షల ముప్పై ఏడు వేల నాలుగు వందల ముప్పై ఆరు.
అంతర్జాతీయ సంఖ్యామానం : 1,028,737,436
ఒక బిలియన్ ఇరవై ఎనిమిది మిలియన్ల ఏడు వందల ముప్పై ఏడు వేల నాలుగు వందల ముప్పై ఆరు.

2011 భారతదేశ జనాభా : 1210193422
హిందూ సంఖ్యామానం : 121,01,93,422
నూట ఇరవై ఒక్క కోటి ఒక లక్ష తొంభై మూడు వేల నాలుగు వందల ఇరవై రెండు.
అంతర్జాతీయ సంఖ్యామానం : 1,210, 193,422
ఒక బిలియన్ రెండు వందల పది మిలియన్ల నూట తొంభై మూడు వేల నాలుగు వందల ఇరవై రెండు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 13]

కింది సంఖ్యలను దగ్గరి పదులకు, వందలకు, వేలకు సవరించండి.
(1) 56,789  (2) 86,289 (3) 4,56,726 (4) 5,62,724
సాధన.

ప్రయత్నించండి [పేజి నెం. 13]

సంఖ్యలను సవరించడం గురించి నీ మిత్రులతో చర్చించు. 2011 జనాభా లెక్కల ప్రకారం ఆంధ్రప్రదేశ్, తెలంగాణ, మరియు భారతదేశ జనాభాలను దగ్గరి లక్షలకు సవరించండి.
సాధన.

[పేజి నెం. 14]

సవరించుట ద్వారా మొత్తాన్ని అంచనా వేసి, ఫలితాన్ని సరిచూడండి.

ప్రశ్న 1.
8756 + 723
సాధన.
8756 + 723
సవరించడం ద్వారా అంచనా వేసిన మొత్తం = 8800 + 700 = 9500
కూడడం ద్వారా మొత్తం –
\(\begin{array}{r}
8756 \\
723 \\
\hline 9,479 \\
\hline
\end{array}\)
9,479 9,479 అనేది 9,500 కు అంచనా వేయడమైనది.

ప్రశ్న 2.
56723 + 4567 + 72 + 5
సాధన.
56,723 + 4,567 + 72 + 5
సవరించడం ద్వారా అంచనా వేసిన మొత్తం = 56,720 + 4,570 + 70 + 10 = 61,370
కూడడం ద్వారా మొత్తం
\(\begin{array}{r}
56,723 \\
4,567 \\
72 \\
5 \\
\hline 61,367 \\
\hline
\end{array}\)
61,367 61,367 అనేది 61,370 కు అంచనా వేయడమైనది.

ప్రశ్న 3.
656724 + 8567
సాధన.
656724 + 8567
సవరించడం ద్వారా అంచనా వేసిన మొత్తం = 6,57,000 + 8,000 = 6,65,000
కూడడం ద్వారా మొత్తము
\(\begin{array}{r}
6,56,724 \\
8,567 \\
\hline 6,65,291 \\
\hline
\end{array}\)
6,65,291 అనేది 6,65,000 కు అంచనా వేయడమైనది.

ప్రశ్న 4.
60756 + 2562 + 72
సాధన.
60756 + 2562 + 72
సవరించడం ద్వారా అంచనా వేసిన మొత్తం = 60,760 + 2,560 + 70 = 63,390
కూడడం ద్వారా మొత్తము
\(\begin{array}{r}
60756 \\
2562 \\
72 \\
\hline 63,390 \\
\hline
\end{array}\)
63,390 అనేది 63,390 కు అంచనా వేయడమైనది.

సవరించడం ద్వారా భేదాన్ని అంచనావేసి, ఫలితాన్ని సరిచూడండి.

ప్రశ్న 1.
7023 – 856
సాధన.
7023 – 856
సవరించడం ద్వారా అంచనా వేసిన భేదం = 7000 – 900 = 6,100
తీసివేయడం ద్వారా భేదం

6,167 ను 6,100 గా అంచనా వేయడమైనది.

ప్రశ్న 2.
9563 – 2847
సాధన.
9563 – 2847
సవరించడం ద్వారా అంచనా వేసిన భేదం = 10,000 – 3,000 = 7,000
తీసివేయడం ద్వారా భేదం

6716 ను 7,000 గా అంచనా వేయడమైనది.

ప్రశ్న 3.
52007 – 6756
సాధన.
52007 – 6756
సవరించడం ద్వారా అంచనావేసిన భేదం = 52,000 – 7,000 = 45,000
తీసివేయడం ద్వారా భేదం

45,251 ను 45,000 గా అంచనా వేయడం జరిగినది.

ప్రశ్న 4.
95625 – 4235
సాధన.
95625 – 4235
సవరించడం ద్వారా అంచనావేసిన భేదం = 95,600 – 4,200 = 91,400
తీసివేయడం ద్వారా భేదం

91,390 ని 91,400 గా అంచనా వేయడమైనది.

[పేజి నెం. 150]

సవరించడం ద్వారా లబ్దాన్ని అంచనా వేసి, ఫలితాన్ని సరిచూడండి.

ప్రశ్న 1.
63 × 85
సాధన.
63 × 85
సవరించడం ద్వారా అంచనా వేసిన లబ్దం = 60 × 90 = 5,400
గుణించడం ద్వారా లబ్దం

5,355 ను 5,400 గా అంచనా వేయడం జరిగినది.

ప్రశ్న 2.
636 × 78
సాధన.
636 × 78
సవరించడం ద్వారా అంచనా వేసిన లబ్దం = 640 × 80 = 51,200
గుణించడం ద్వారా లబ్ధం

49,608 ని 51,200 గా అంచనా వేయడం జరిగినది.

ప్రశ్న 3.
506 × 85
సాధన.
506 × 85
సవరించడం ద్వారా అంచనా వేసిన లబ్ధం = 500 × 90 = 45000
గుణించడం ద్వారా లబ్దము

43,010 ని 45,000 గా అంచనా వేయడం జరిగినది.

ప్రశ్న 4.
709 × 98
సాధన.
709 × 98
సవరించడం ద్వారా అంచనా వేసిన లబ్దం = 700 × 100 = 70,000
గుణించడం ద్వారా లబ్దం

69,482 ను 70,000 గా అంచనా వేయడం జరిగినది.

సవరించుట ద్వారా భాగహారాన్ని అంచనా వేసి, ఫలితాన్ని సరిచూడండి.

ప్రశ్న 1.
936 ÷ 7
సాధన.
936 ÷ 7 : సవరించుట ద్వారా అంచనా వేసిన భాగఫలం 1000 ÷ 10 = 100
భాగహారం ద్వారా భాగఫలం = 133

133 ను 100 గా అంచనా వేయడం జరిగినది.

ప్రశ్న 2.
956 ÷ 17
సాధన.
956 ÷ 17 : సవరించడం ద్వారా అంచనా వేసిన భాగఫలం = 1000 ÷ 20 = 50
భాగహారం ద్వారా భాగఫలం = 56

56ను 50 గా అంచనా వేయడం జరిగినది.

ప్రశ్న 3.
859 ÷ 23
సాధన.
859 ÷ 23 : సవరించడం ద్వారా అంచనా వేసిన భాగఫలం = 860 ÷ 20 = 43
భాగహారం ద్వారా భాగఫలం = 37

37 ను 43 గా అంచనా వేయడం జరిగినది.

ప్రశ్న 4.
708 ÷ 32
సాధన.
708 ÷ 32
సవరించడం ద్వారా అంచనా వేసిన భాగఫలం = 710 ÷ 30 = 23
భాగహారం ద్వారా భాగఫలం = 22

22 ను 23 గా అంచనా వేయడం జరిగినది.

ఉదాహరణలు

ప్రశ్న 1.
కింది సంఖ్యలను పోల్చి ఆరోహణ మరియు అవరోహణ క్రమంలో రాయండి.
29,845 | 29,923 | 38,962 | 1,26,845 | 8,496 | 36,897
సాధన.
ఆరోహణ క్రమం :
ఆరోహణ క్రమము అనగా సంఖ్యలను కనిష్ఠ సంఖ్య నుండి గరిష్ఠ సంఖ్యకు అమర్చటం.
8,496, 29,845, 29,923, 36,897, 38,962, 1,26,845
అవరోహణ క్రమం :
అవరోహణ క్రమం అనగా సంఖ్యలను గరిష్ఠ సంఖ్య నుండి కనిష్ఠ సంఖ్యకు అమర్చటం.
1,26,845, 38,962, 36,897, 29,923, 29,845, 8,496

ప్రశ్న 2.
కామాలుంచి కింది సంఖ్యలను గ్రూపులుగా విభజించి, వాటిని పద రూపంలో రాయండి.
అ) 356485
ఆ) 4075675
ఇ) 7056702725
సాధన.
అ) 356485 ను కామాలుంచి గ్రూపులుగా వేరు చేసి 3,56,485 గా రాయవచ్చు.
దీనిని “మూడు లక్షల యాభై ఆరు వేల నాలుగు వందల ఎనభై ఐదు” అని రాయవచ్చు.
ఆ) 4075675 ను కామా ఉంచి గ్రూపులుగా వేరు చేసి 40,75,675 గా రాయవచ్చు.
దీనిని “నలభై లక్షల డెబ్బై ఐదు వేల ఆరువందల డెబ్బై ఐదు” అని రాయవచ్చు.
ఇ) 7056702725 ను కామాలుంచి గ్రూపులుగా వేరుచేసి 705,67,02,725 గా రాయవచ్చు.
దీనిని “ఏడు వందల ఐదు కోట్ల అరవై ఏడు లక్షల రెండు వేల ఏడు వందల ఇరవై ఐదు” అని రాయవచ్చు.

ప్రశ్న 3.
కింది వాటిని సంఖ్యా రూపంలో రాసి సరియైన విధంగా కామాలనుంచండి.
అ) నాలుగు కోట్ల నాలుగు లక్షల నాలుగు వేల నాలుగు వందల నాలుగు.
ఆ) తొంభై ఐదు కోట్ల అరవై లక్షల డెబ్బై రెండు వేల నాలుగు వందల ఇరవై ఐదు.
సాధన.
అ) నాలుగు కోట్ల నాలుగు లక్షల నాలుగు వేల నాలుగు వందల నాలుగు. 4,04,04,404
ఆ) తొంభై ఐదు కోట్ల అరవై లక్షల డెబ్బై రెండు వేల నాలుగు వందల ఇరవై ఐదు. 95,60,72,425

ప్రశ్న 4.
857065723 అనే సంఖ్యలో ‘7’ల స్థాన విలువల భేదాన్ని కనుగొనండి.
సాధన.
ఇచ్చిన సంఖ్య 857065723. గ్రూపులుగా విభజించుటకు సరైన విధంగా కామాలుంచిన దీనిని 85,70,65,723 గా రాయవచ్చు.
వందల స్థానంలో గల ‘7’ యొక్క స్థాన విలువ : 7 × 100 = 700
పది లక్షల స్థానంలో గల ‘7’ యొక్క స్థాన విలువ = 7 × 10,00,000 = 70,00,000
కావలసిన భేదం = 70,00,000 – 700 = 69,99,300

అంతర్జాతీయ సంఖ్యామానంలో గల సంఖ్యలను చదవటానికి ప్రయత్నిద్దాం.

ప్రశ్న 5.
78123
సాధన.
సోపానం – 1: ప్రతి మూడు స్థానాలకు కామాలుంచాలి. ఉదా : 78,123
సోపానం – 2: విస్తరణ రూపం :
78123 = 7 × 10,000 + 8 × 1,000 + 1 × 100 + 2 × 10+ 3 × 1
సోపానం – 3: అక్షర రూపం : డెబ్బై ఎనిమిది వేల నూట ఇరవై మూడు.

ప్రశ్న 6.
934567
సాధన.
సోపానం – 1: ప్రతి మూడు స్థానాలకు కామాలుంచాలి. ఉదా : 934,567
సోపానం – 2: విస్తరణ రూపం :
934567 = 9 × 100,000 + 3 × 10,000 + 4 × 1,000 + 5 × 100 + 6 × 10 + 7 × 1
సోపానం – 3: అక్షర రూపం : తొమ్మిది వందల ముఫ్పై నాలుగు వేల ఐదు వందల అరవై ఏడు.

ప్రశ్న 7.
9924067256
సాధన.
సోపానం – 1: ప్రతి మూడు స్థానాలకు కామాలుంచాలి. ఉదా : 9,924,067,256
సోపానం – 2: విస్తరణ రూపం :
9 × 1,000,000,000 + 9 × 100,000,000 + 2 × 10,000,000 + 4 × 1,000,000 + 0 × 100,000 + 6 × 10,000 + 7 × 1,000 + 2 × 100 + 5 × 10 + 6 × 1
సోపానం – 3 : అక్షర రూపం :
తొమ్మిది బిలియన్ల తొమ్మిది వందల ఇరవై నాలుగు మిలియన్ల అరవై ఏడు వేల రెండు వందల యాభై ఆరు.

ప్రశ్న 8.
536724 ను దగ్గరి పదులకు, వందలకు, వేలకు సవరించండి.
సాధన.
i) దగ్గరి 10 కి సవరించుట : ఇచ్చిన సంఖ్య 5,36,724
పదుల స్థానానికి కుడివైపు అంకె 4. 4 < 5 కావున కిందికి సవరించాలి. 5,36,720.
ii) దగ్గరి 100 కి సవరించుట : ఇచ్చిన సంఖ్య 5,36,724
వందల స్థానానికి కుడివైపు అంకె 2. 2 < 5 కావున కిందికి సవరించాలి. 5,36,700.
iii) దగ్గరి 1000 కి సవరించుట : ఇచ్చిన సంఖ్య 5,36,724
వేల స్థానానికి కుడివైపు నున్న అంకె 7. 7 > 5 కావున పైకి సవరించాలి. 5,37,000.

SCERT AP 6th Class Maths Solutions Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు Unit Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 1st Lesson మన చుట్టూ ఉండే సంఖ్యలు Unit Exercise

ప్రశ్న 1.
కింది వాటిని అంకెలలో రాయండి.
అ) వంద కోట్ల, వంద వేలు మరియు వంద.
సాధన.
100,01,00,100

ఆ) 20 బిలియన్ల నాలుగు వందల తొంభై ఏడు మిలియన్ల తొంభై ఆరు వేల నాలుగు వందల డెబ్బై రెండు.
సాధన.
20,497,096,472

ప్రశ్న 2.
కింది సంఖ్యలను హిందూ సంఖ్యామానంలో మరియు అంతర్జాతీయ సంఖ్యామానంలోనూ అక్షరాలలో రాయండి.
అ) 8275678960
ఆ) 5724500327
ఇ) 1234567890
సాధన.
అ) 8275678960
హిందూ సంఖ్యామానం : 827,56,78,960
ఎనిమిది వందల ఇరవైఏడు కోట్ల యాభై ఆరు లక్షల డెబ్బై ఎనిమిది వేల తొమ్మిది వందల అరవై.
అంతర్జాతీయ సంఖ్యామానం : 8,275,678,960
ఎనిమిది బిలియన్ల రెండు వందల డెబ్బై ఐదు మిలియన్ల ఆరు వందల డెబ్బై ఎనిమిది వేల తొమ్మిది వందల అరవై.

ఆ) 5724500327
హిందూ సంఖ్యామానం : 572,45,00,327
ఐదు వందల డెబ్బై రెండు కోట్ల నలభై ఐదు లక్షల మూడు వందల ఇరవై ఏడు.
అంతర్జాతీయ సంఖ్యామానం : 5,724,500,327
ఐదు బిలియన్ల ఏడు వందల ఇరవై నాలుగు మిలియన్ల ఐదు వందల వేల మూడు వందల ఇరవై ఏడు.

ఇ) 1234567890
హిందూ సంఖ్యామానం : 123,45,67,890
నూట ఇరవై మూడు కోట్ల నలభై ఐదు లక్షల అరవై ఏడు వేల ఎనిమిది వందల తొంభై.
అంతర్జాతీయ సంఖ్యామానం : 1,234,567,890
ఒక బిలియన్ రెండు వందల ముప్పై నాలుగు మిలియన్ల ఐదు వందల అరవై ఏడు వేల ఎనిమిది వందల తొంభై.

ప్రశ్న 3.
98978056 సంఖ్యలో 8 ల స్థాన విలువల భేదాన్ని కనుగొనండి.
సాధన.
హిందూ సంఖ్యామానం :
ఇచ్చిన సంఖ్య = 9,89,78,056

అంతర్జాతీయ సంఖ్యామానం :
ఇచ్చిన సంఖ్య = 98,978,056

ప్రశ్న 4.
ఆరు అంకెల సంఖ్యలెన్ని ఉన్నాయి?
సాధన.
ఆరు అంకెల పెద్ద సంఖ్య = 9,99,999
ఆరు అంకెల చిన్న సంఖ్య = 1,00,000
ఆరు అంకెలు కలిగిన మొత్తం సంఖ్యల సంఖ్య = 9,99,999 – 1,00,000 + 1 = 9,00,000

ప్రశ్న 5.
ఎన్ని వేలయితే ఒక మిలియన్ అవుతుంది?
సాధన.
1 మిలియన్ = 1,000,000 = 1000 వేలు
1 మిలియన్ = 1,000 వేలు

ప్రశ్న 6.
‘5’ మొబైల్ నంబర్లను సేకరించి వాటిని ఆరోహణ మరియు అవరోహణ క్రమాలలో రాయండి.
సాధన.
ఏవైనా 5 మొబైల్ నంబర్లు : 9247568320, 9849197602, 8125646682, 6305481954, 7702177046
ఆరోహణక్రమం : 6305481954, 7702177046, 8125646682, 9247568320, 9849197602
అవరోహణక్రమం : 9849197602, 9247568320, 8125646682, 7702177046, 6305481954

ప్రశ్న 7.
ప్రవళికి ఒక సోదరి మరియు ఒక సోదరుడు ఉన్నారు. ప్రవళి తండ్రిగారు 1 మిలియన్‌ రూపాయలను సంపాదించి వారికి సమానంగా పంచదలచారు. ప్రతి ఒక్కరూ పొందే సొమ్మును (సుమారు) లక్షలలో అంచనావేసి, భాగహారం చేసి సరిచూడండి.
సాధన.
ఒక మిలియన్ = 10,00,000 = 10 లక్షలు
ప్రవళి తండ్రిగారు 1 మిలియన్ (10 లక్షలు) రూపాయలను ముగ్గురు పిల్లలకి సమానంగా పంచదలిచారు.
ఒక్కొక్కరికి పంచిన సొమ్ము = 10 లక్షలు + 3 = ₹ 3,33,333
= ₹3,00,000 (సుమారుగా)

ప్రశ్న 8.
బ్యాంకు ప్రతి రైతుకు ₹ 13,500 ఋణం ఇవ్వాలనుకుంది. ఒక జిల్లాలో 2,27,856 రైతులున్నారు. అయిన బ్యాంకు, ఆ జిల్లాలోని రైతులందరికి ఋణం ఇవ్వడానికి అవసరమైన సొమ్మును అంచనా వేయండి. లెక్కించండి.
సాధన.

ప్రశ్న 9.
క్యూసిక్, టి.యం.సి., మెట్రిక్ టన్ను, కిలోమీటరు పదాలను వివరించండి.
సాధన.
i) క్యూసెక్ : ఒక్క సెకను కాలంలో ఎన్ని ఘనపుటడుగులు ప్రవాహం ద్వారా ప్రయాణిస్తున్నాయో ఆ సంఖ్యను క్యూసెక్ (cubic feet per second) అంటారు.
1 క్యూసెక్ = 0.028316 ఘనపుటడుగులు (ఒక సెకను కాలం)
= 28.316 లీటర్లు (సెకనుకి)
ద్రవాల ఘనపరిమాణాన్ని బ్రిటిష్ కొలమానమైన fps (foot-pound-second) ప్రమాణాలలో ఘనపుటడుగు (cubic foot) లలో కొలుస్తారు.

ii) టి.యం.సి. : వేయి మిలియన్ల ఘనపుటడుగులు లేదా టి.యం.సి. అనే పదాన్ని సాధారణంగా జలాశయం లేదా నది ప్రవాహంలో నీటి పరిమాణాన్ని సూచించేందుకు ఉపయోగిస్తారు.
1 టి.యం.సి. = 0.28316000000 లీటర్లు
= 28.316 బిలియన్ లీటర్లు
= 2831.6 కోట్ల లీటర్లు

iii) మెట్రిక్ టన్ను : బరువులను కొలవడానికి మెట్రిక్ టన్నును ప్రమాణంగా వాడతారు.
మెట్రిక్ టన్ను = 1000 కి.గ్రా. = 10 క్వింటాళ్ళు
వరి, పప్పులు కొలవటానికి మెట్రిక్ టన్నును ప్రమాణంగా వాడతారు.

iv) కిలోమీటరు : పొడవులను కొలవడానికి కిలోమీటరును ప్రమాణంగా వాడతారు.
1 కిలోమీటరు = 1000 మీ.
పల్లెలు, గ్రామాలు, పట్టణాల మధ్య దూరాలను కొలవడానికి దీనిని వాడతారు.