Inter 2nd Year

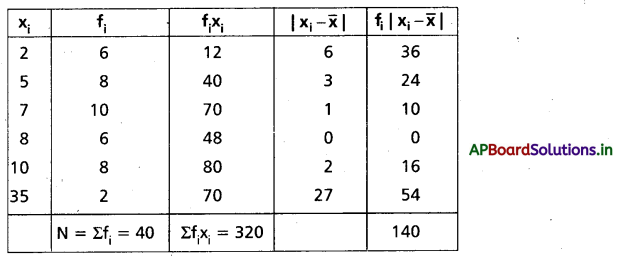
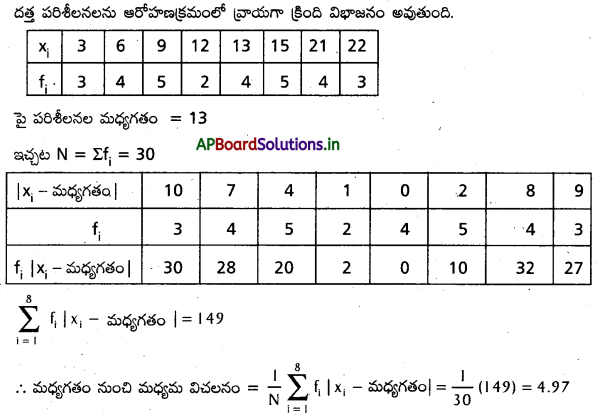
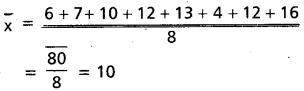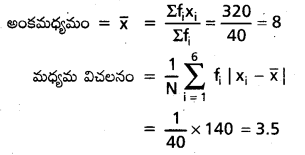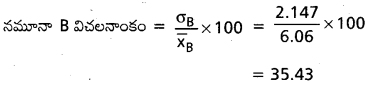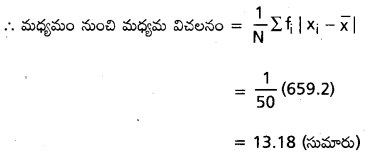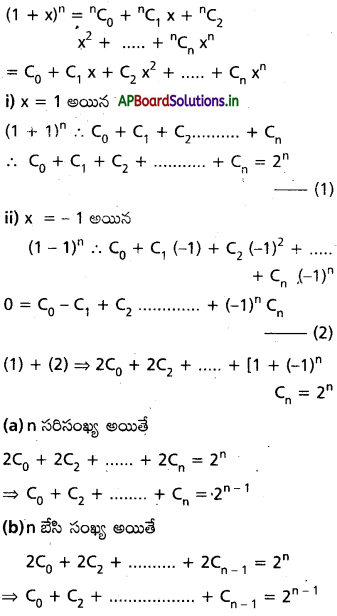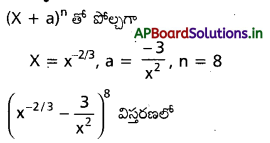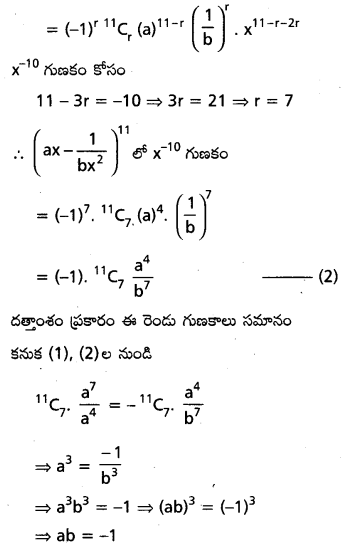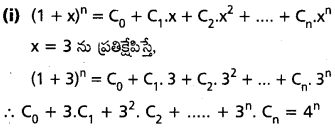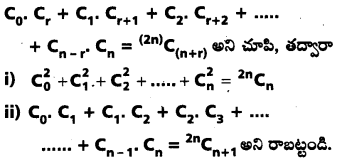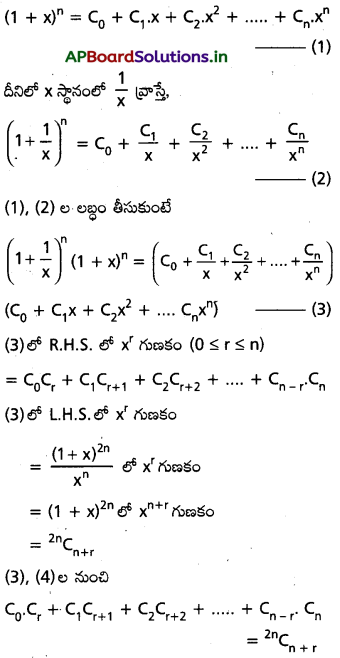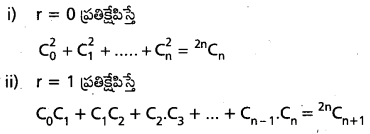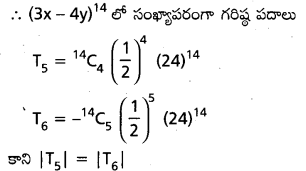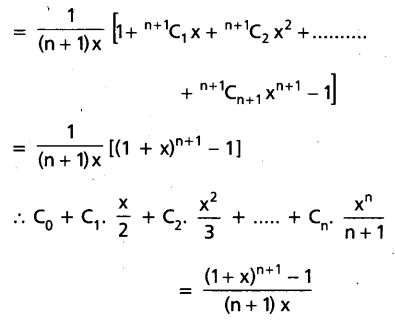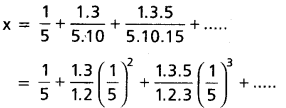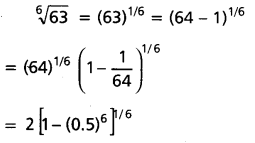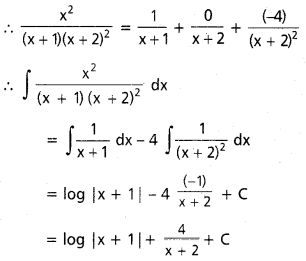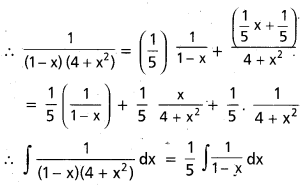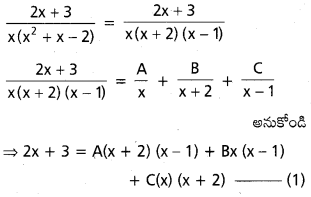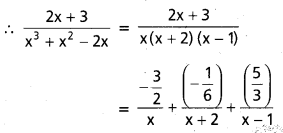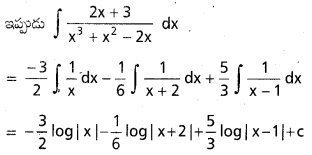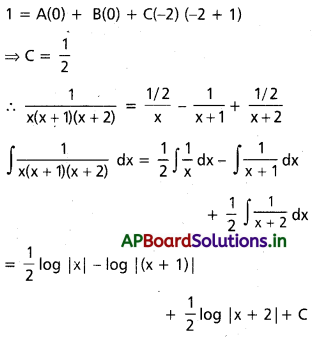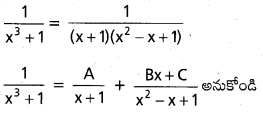Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 9 సంభావ్యత which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 9 సంభావ్యత

ప్రశ్న 1
రెండు పాచికలను ఒకే తడవ దార్లంచినప్ణుడు ఆ పాచికల ముఖాలపై ఒకే సంఖ్ల రావడానికి గల సంఖావ్యతను కనుక్కోండి.
సాధన:
రెండు పాచికల ముఖాలపై ఒకే సంఖ్య వచ్చే ఘటనను ‘E’ అనుకొందాం.
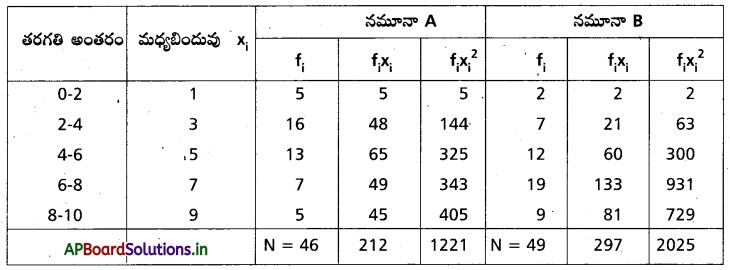
‘E’ జరగడానికి దోహదం చేసే సందర్భాల సంఖ్య = 6 శాంపిల్ ఆవరణంలోని మొత్తం లఘు ఘటనల సంఖ్య

ప్రశ్న 2.
1 నుంచి 20 వరకు గల 20 సంఖ్లల నుంచి ఒక సంఖ్యను ఎన్నుకొన్నాం. ఆ సంఖ్య ప్రధాన సంఖ్య అయ్యే సంభావ్యతను కనుక్కోండి.
సాధన:
శాంపుల్ ఆవరణ S లో 20 మూలకాలున్నాయి. ఎన్నుకన్న సంఖ్య ప్రధాన సంఖ్య అయ్యే ఘటన E అనుకోండి. అప్పుడు

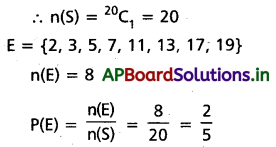
ప్రశ్న 3.
ఒక సంచిలో 4 ఎర్రని, 5 నల్లని, 6 నీలం రంగును కలిగిన ఐంతులున్నాయి. యాదృచ్చింగా ఏకకాలంలో ఎన్నుకొన్న రెండు బంతులలో ఒకట ఎర్రది అయ్యే సంభావ్యతను కనుక్కోండి.
సాధన:
రెండు బంతులను ఒకసారి తీసినపుడు ఒకటి నల్ల బంతి, ఒకటి ఎర్రబంతి వచ్చే ఫుటన ‘E’ మరియు ‘S’ అనేది శాంపుల్ ఆవరణం. నంచిలోని వెుత్తం బంతుల నంఖ్ = 4+5+6 = 15

ప్రశ్న 4.
పది పాచికలను ఒకే తడవ దొర్లించినప్పుడు అందుల ఏ పాచికా 1 చూపకపోవడానికి గల సంభావ్యతను కనుక్కోండి.
సాధన:
ఏ పాచిక 1 చూపని ఘటనను A అనుకొందాం.

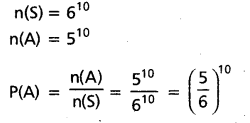
ప్రశ్న 5.
{1,2,3, ………… 100} నుంచి ఒక సంఖ్య x ను యాదృచ్ఛికంగా తీయడంజరిగింది. \(\left(x+\frac{100}{x}\right)\)> 29 అయ్యే సంఖావ్యత ఎంత?
సాధన:
ఇక్కడ మొత్తం ఫలితాల సంఖ్య 100.
{1,2,3, ………….. 100} లో నుంచి ఎన్నుకొన్న సంఖ్య x
అనేది \({x}+\frac{100}{\mathrm{x}}\) > 29 ని ధ్రువపరిచే ఘటనను A అనుకొందాం.
అప్పుడు x+ \(\frac{100}{\mathrm{x}}\) >29
⇔ x² -29 x+100 > 0
⇔ (x-4)(x-25) > 0
⇔ x < 4 లేదా x > 25
⇔ x ∈ {1,2,3,26,27, ………………….. 100} = A (అనుకొందాం)
∴ A అనుకూల ఫలితాల సంఖ్య 78
∴ కావలసిన సంభావ్యత = P(A) = \(\frac{78}{100}\) = 0.78

ప్రశ్న 6.
ఒక చదరంగం బల్లపై రెండు చతురస్రాలను యాదృచ్ఛికంగా ఎన్నుకొన్నారు. వాటికి ఉమ్మడి భుం ఉండటానికి గల సంభావ్యత \(\frac{1}{18}\) అని చూపండి.
సాధన:
మొదటి చతురస్సాన్ని 64 విధాలుగా, రెండోదాన్ని 63 విధాలుగా ఎన్నుకోవచ్చు.
కాబట్టి రెండు చతురస్సాలను ఎన్నుకొనే విధాలు 64× 63
ఈ చతురస్రాలు ఒక ఉమ్మడి భుజాన్ని కలిగిఉండే ఘటన E అనుకొందాం.
ఇప్పుడు E అనుకూల ఫలితాల సంఖ్యను కనుక్కొందాం. మొదటగా ఎగ్నుకొన్న చతురస్రం మూలనున్న నాలుగు చతురస్సాల్లో ఒకటి అయితే రెండో చతురస్సాన్ని (ఉమ్మడి భుజం ఉండేటట్లు) రెండు రకాలుగా ఎన్నుకోవచ్చు.
మొదటిగా ఎన్నుకొన్న చతురస్సం చదరంగం ఐల్ల భుజం వెంబడి గల (మూలల వద్ద ఉన్నవాటిని మినహాయిస్తే) 24 చదరాల్లో ఒకటి అయితే, రెండో చతురప్రాన్ని 3 విధాలుగా ఎన్నుకోవచ్చు.
మొదటిగా ఎన్నుక్న్న చతురక్సం మిగిలిన 36 చతురస్సాల్లో ఒకటి అయితే రెండోదాన్ని 4 విధాలుగా ఎన్నుకోవచ్చు.
కాబట్టి అనుకూల ఫలితాల సంఖ్
(4 × 2)+(24 × 3)+(36 × 4)=224
∴ కావలసిన సంభావ్యత = \(\frac{224}{64 \times 63}=\frac{1}{18}\)

ప్రశ్న 7.
ఒక నిష్బాక్షక నాణేన్ని 200 సార్లు ఎగరవేశారు. జేసి సంఖ్యలో (అన్నిసార్ల) ణొమ్మహడే సంఖావ్యత కనుక్కోండి.
సాధన:
మొత్తం ఫలితాల సంఖ్య 2²⁰⁰
బేసి సంఖ్యలో దొమ్మపడే ఘటనను E అనుకొందాం.
E కి అనుకూల ఫలితాల సంఖ్య

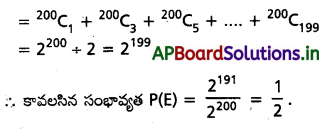
ప్రశ్న 8.
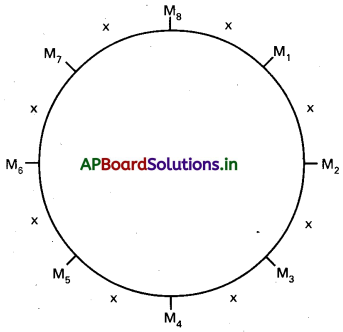
యాదృచ్ఛికంగా ఒక గుండ్రని ణల్ల చుట్టా కూర్చన్న 20 మంది వ్యక్తలలో A, Bలు ఉన్నారు. A, Bల మధ్య ఎవరైనా ఆరుగురు వ్యక్తులండే సంఖావ్యత కనుక్రోండి.
సాధన:
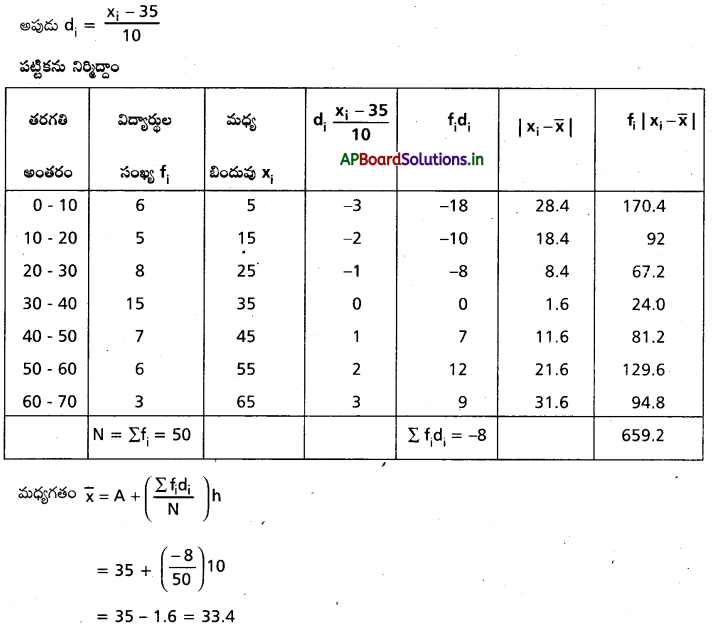
గుండ్రటి బల్లచుట్టూ ఏ ఆసనం పైనెనా ‘A’ కూర్చోవచ్చు. అప్పుడు Bకి అందుబాటులో ఉన్న ఆసనాల సంఖ్ 19. కాని A, Bల మధ్య ఆరుగురు వ్యక్తులు ఉండాలంటే Bకి గల అవకాశాలు రెండే.
∴ కావలసిన సంభావ్యత \(\frac{2}{19}\).

ప్రశ్న 9.
30 వరస హార్ణాంకాల నుంచి రెండింటిని యాదృచ్కంగా ఎన్నకకొన్నారు. వాటి మొత్తం జేసససంఖ్య అజ్యే సంఖావ్యత ఎంత ?
సాధన:
30 సంఖ్యల నుంచి 2 సంఖ్యలను ఎన్నుకొనే విధాలు ³⁰C₂. ఈ 30 సంఖ్లల్లో 15 సంఖ్యలు జేసి కాగా 15 సంఖ్యలు సరి సంఖ్యలు. ఎన్నుకొన్న రెండు సంఖ్యల మొత్తం బేసిసంఖ్య కావాలంటే అందులో ఒకటి సరిసంఖ్య మరాకటి దేసిపంఖ్య కావాలి. కాబట్టి అనుకూల ఫలిజాల సంఖ్య = ¹⁵C₁ x ¹⁵C₁
∴ కావలసిన సంభావ్యత

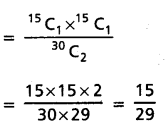
ప్రశ్న 10.
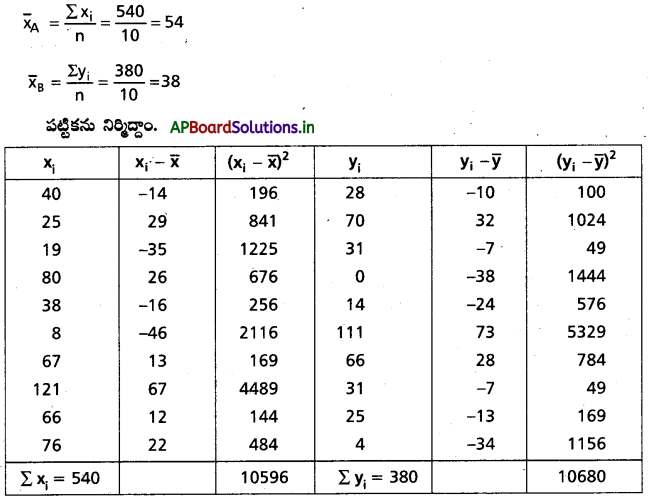
పుట్టిన పిల్లలు 1,00,000 మందిలో 20 సంవత్సరాల వయస్సు వచ్చే వరకు జీవించేవారి సంఖ్య 77,181. ఇప్పుడు పుట్టిన ఐిడ్డ 20 సంవత్సరాల వరకు జీవించగల సంఖావ్యతను కనుక్కోండి.
సాధన:
ఇక్కడ m=77,181
n=1,00,000
కావలసిన సంభావ్యత = \(\frac{m}{n} = \frac{77,181}{1,00,000}\)
= 0.77181

ప్రశ్న 11.
సంఖావ్యతకు సంకలన సిద్ధాంతం.
సాధన:
ప్రవచనం : ఒక యాదృచ్ఛిక ప్రయోగంలో E₁, E₂ ఏవైనా రెండు ఘటనలు, P సంభావ్యతా ప్రమేయం అయితే

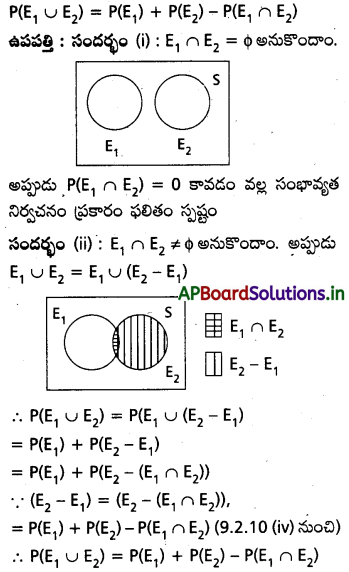
ప్రశ్న 12.
రెండు పాణికలతో మొత్తం స్కోరు 7 దొర్లించే సంఖావ్యత ఎంత ?
సాధన:
ఇచ్చిన (పయోగం శాంపిల్ ఆవరణం
S={(1,1),(1,2), ……………… (1,6),
(2,1),(2,2), …………….. ,(2,6),
..
..
..
..
(6,1,(6,2), …………….. ,(6,6)}
ఏదైనా ఒక మూలకంలోని మొదటి నిరూపకం మొదటి పాచికపై స్కోరును, రెండో నిరూపకం రెండో పాచికపై స్కరును సూచిస్తాయి. Sలో మొత్తం 36 మూలకాలున్నాయి. S లోని మూలకాలన్నీ సమసంభవాలు.
మొత్తం స్కోరు 7 పొందే ఘటనను E అనుకోండి. అప్పుడు
E={(1,6),(2,5),(3,400),(4,3),(5,2), (6,1)}, E లో మొత్తం 6 మూలకాలున్నాయి.
∴ P(E) = \(\frac{6}{36}\) = \(\frac{1}{6}\)

ప్రశ్న 13.
మాడు నాణేలను ఎగరవేసినప్పండు రెండు ణొరుసులు, ఒక జొమ్ము పొందే సంఖావ్యత ఎంత ?
సాధన:
మూడు నాణేలను ఎగరవేసే ప్రయోగం శాంపిల్ ఆవరణం S = {H H H, H H T, H T H, H T T, T H H, T H T, T T H,TT T}
n(S)=, 8
రెండు బొరుసులు, ఒక దొమ్మ పడే ఘటనను E అనుకోండి.
అప్పుడు E = {H TT, T H T, TT H}
\(P(E)=\frac{n(E)}{n(S)}=\frac{3}{8}\)
∴ P(E) \(\frac{3}{8}\)

ప్రశ్న 14.
200 పేజీలు గల ఒక పుస్తకంలో నుంచి ఒక పేజీని యాదృచ్చికంగా తెరిచారు. పేజీ సంఖ్య సంపూర్ద వర్గమయ్యే సంఖావ్యత ఎంత ?
సాధన:
పై సమస్యలోని ప్రయోగపు శాంపిల్ ఆవరణం
S = {1,2,3, ………………… , n(S) = 200
తెరిచిన పేజీపై సంఖ్య సంపూర్ణ వర్గమయ్యే ఘటన E అనుకోండి. అప్పుడు
E = {1,4,9, ………………….. 196}, n(E)=14
\(P(E)=\frac{n(E)}{n(S)}=\frac{14}{200}=\frac{7}{100}=0.07\)

ప్రశ్న 15.
బాగా కలిపిన 52 పేకముక్కల కట్ట నుంచి ఒక ముక్కను తీస్తే అది ఆసు గాని, ఇన్పేటి గాని అహ్యే సంఖావ్యత ఎంత? గమనిక : పేక ముక్కల కట్ట అంటే 52 కార్కులు ఉన్న పేక ముక్కల కట్ట అని అర్థం. అందులో 26 ఎర్రనివి, 26 నల్లనివి. ఈ 52 కార్డును నాలుగు సెట్లుగా విభజిస్తూ వీటిని ఆఠీను, కళావరు, డైమండ్, స్పేడ్ (ఇస్పేటు) అనే పేర్లతో పిలుస్తారు. ప్రతి సెట్లోనూ 13 కార్డులుంటాయి. అవి A, 2,3,4,5,6,7,8,9,10, K, Q, J
( A= ఆసు, K= రాజు, Q= రాణి, J = జాకీ)
సాధన:
తీసిన ముక్క ఇస్పేటు అయ్యే ఘటన E₁, ఆసు అయ్యే ఘటన E₂ అనుకోండి. E₁, E₂ లు పరస్పర వివర్జిత ఘటనలు కావని గమనించండి. P(E₁ ∪ E₂) ని కనుక్కోవాలి.

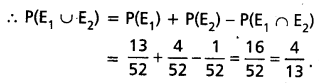
ప్రశ్న 16.
A, B లు రెండు ఘటనలైతే
(i) P(A∩B^c)=P(A) – P(A∩B),
(ii) A, B లలో ఒక్కటి మాత్రమే జరిగే సంభావ్యత P(A)+P(B) – 2P(A∩B) అని చూపండి.
సాధన:

ప్రశ్న 17.
A, B ఫటనలల P(A)=0.5, P(B)=0.4, P(A∩B) = 0.3 అయ్యేటట్లు ఉన్నాయనుకోండ.
i) A జరగకపోవడానికి
ii) A కానీ, B కానీ (A, B లు రెండూ) జరగకపోవడానికి సంభావ్యతలను కనుక్కోండి.
సాధన:
i) A జరగకపోమే ఘటన A^c; A కానీ, B కానీ జరగకపోయే ఘటన P(A∪B)^c , అని మనకు తెలుసు.
∴ P(A^c) = 1 – P(A) = 1 – 0.5 = 0.5

ii) P(A∪B) = P(A) + P(B) – P(A∩B)
కాబట్టి P(A∪B) = 0.5 + 0.4 – 0.3
= 0.6
∴ P[(A∪B)^c ] = 1 P(A∪B)
= 1 – 0.6 = 0.4

ప్రశ్న 18.
A, B, C లు మాడు ఘటనలైతే, P(A∪B∪C) P(A) + P(B) + P(C)  – P(A∩B) – P(B∩C) – p(C∩A) + P(A∩B∩C) అని చూపండి.
సాధన:
B∪C = D అని వ్రాస్తే P(A∪B∪C) = P(A∪D)
P(A∪D) = P(A) + P(D) – P(A∩D)

ప్రశ్న 19.
సంభావ్యతకం గుణాన సిద్ధాంతం.
సాధన:
ప్రవచనం : P(A)>0, P(B) > 0 తో A, B లు ఒక యాద్చిక (పయోగపు ఘటనలు అయితే,
P(A∩B)=P(A) P(B|A)=P(B) P(A|B)
ఉపపత్తి : యాద్యచ్చక (పయోగంతో సాహచర్యమైన శాంపల్ ఆవరణాన్ని S అనుకొందాం.
P(A) > 0, P(B) > 0 అయ్యేటట్లుగా A, B లు S లో ఘటనలు. అప్పుడు షరతు సంభావ్యత నిర్వచనం నుంచి,
\(P(B \mid A)=\frac{P(A \cap B)}{P(A)}\)
∴ P(B∩A) = P(A).P(B|A)
P(B) > 0 కాబట్టి పై సమీకరణంలో A, B లను తారుమారు (వినియమం) చేస్తాం.
P(A∩B)=P(B∩A)=P(B).P(A|B)

ప్రశ్న 20.
ఒక పాచిక ఆ యుగ్మాన్ని దార్లించారు. పాచికలపై సంఖ్యల మొత్తం 6 అయినప్పుడు వాటిలో ఏదో ఒకట 2ను చూపే సంభావ్యత ఎంత ?
సాధన:
రెండు పాచికలను దొర్లంచినప్పుడు, ఏదైనా ఒక పాచికపై 2 వచ్చే ఘటన ‘A’, పాచికలపై సంఖ్యల మొత్తం 6 అయ్యే ఘటన ‘B’ అనుకొందాం.
A = {(2,1),(2,2),(2,3),(2,4),(2,4),(2,5),(2,6),(1,2),(3,2),(4,2),(5,2),(6,2)}
n(A) = 11
P(A) = \(\frac{11}{36}\)
B = {(1,5),(2,4),(3,3),(4,2)(5,1)}
n(B)=5
P(B)= \(\frac{5}{36}\)
A∩B = {(2,4),(4,2)}

ప్రశ్న 21.
ఒక పెట్టెలో 4 పనిచేయని, 6 పనిచేసే బల్టలి ఉన్నాయి. దీని నుంచి తీసిన బల్బాను తిరి భర్తీచేయని రీతిలో రెండు ఐల్బులను తీశారు. తీసిన రెండు బల్బులు పనిచేసే ఐల్కాలు అమ్యే సంభావ్యతను కనుక్రోండి.
సాధన:
పది బంతులలో 6 బంతులు ఎర్రటివి కాబట్టి ముందుగా తీసిన బంతి ఎర్రటిదయ్యే సంభావ్యత ‘A’ రెండోసారి తీస్తే ఎర్రటిదయ్యే సంభావ్యత ‘B’, మరియు ‘S’ అనేది శాంపిల్ల ఆవరణం అనుకొందాం.

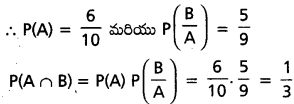
ప్రశ్న 22.
ఒక తరగతిలో పన్నెండుమంది బాలురు, నలుగురు బాలికలున్నారు. ఒకరి తరువాత ఒకరిని వరుసగా ముగ్గురు పిల్లలను ఎన్నుకొంటే, ఆ ముగ్గురూ బాలురు ఆయ్యే సంభావ్యత ఎంత ?
సాధన:
iవ ప్రయత్నంలో బాలుడిని ఎన్నుకొనే ఘటన E_i  అనుకొందాం.
అప్పుడు కనుక్కోవలసిన సంభావ్యత
(i = 1,2,3) P(E₁∩E₂∩E₃) లబ్ద సిద్ధాంతం నుంచి,
P(E₁∩E₂∩E₃) = P(E₁) P(E₂/E₁) P(E₃/E₁∩E₂)
\(=\frac{12}{16} \times \frac{11}{15} \times \frac{10}{14}=\frac{11}{28}\)

ప్రశ్న 23.
75 % సందర్భాలలో A నిజం మాట్లాడతాడు, B 80% సందర్భాలలో B నిజం మాట్లాడతాడు. ఒక సంఘటన గురించి వారు చెప్పే విషయం పరస్పరం విభేదించడానికి సంభావ్యత ఎంత ?
సాధన:
ఒక సంఘటన గురించి A, B లు నిజం చెప్పే ఘటనలు వరుసగా E₁, E₂ అనుకోండి. అప్పుడు

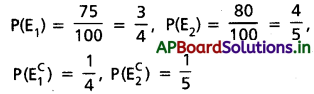
ఒక సంఘటన గురించి వారు చెప్పే విషయం పరస్పరం విభేదించే ఘటన E అనుకొండాం. ఇది రెండు విధాలుగా జరగవచ్చు.
i) A నిజం, B అబద్ధం చెబుతాడు.
ii) A అబద్ధం, B నిజం చెబుతాడు.

ప్రశ్న 24.
కలన గణితంలోని ఒక సమస్యను ఇద్దరు విద్యార్థులు A, Bలకు ఇస్తే వారు సమస్యను సాధించే సంభావ్యతలు వరుసగా \(\frac{1}{3}\), \(\frac{1}{4}\). వారిద్దరూ స్వతంత్గా సమస్యను సాధించడానికి (పయత్నిస్తే, ఆ సమస్ల సాధించగల సంభావ్యత ఎంత ?
సాధన:
A, Bలతో సమస్య సాధించబడే ఘటనలు వరుసగా E₁, E₂ లు అనుకుందాం.
దత్తాంశం ప్రకారం
\(\mathrm{P}\left(\mathrm{E}_1\right)=\frac{1}{3}, \mathrm{P}\left(\mathrm{E}_2\right)=\frac{1}{4}\)
ఈ రెండు ఘటనలు, స్వతంత్త ఘటనలని గమనిద్దాం.
కాబట్టి కావలసిన సంభావ్యత

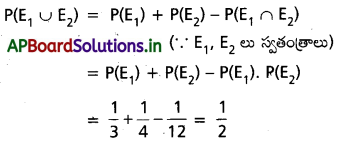
ప్రశ్న 25.
A, B లు ఒక్కొక్కరు ఒక నాణేన్ని 50 సార్లు ఏకకాలంలో ఎగరవేస్తారు. ఇద్దరికీ ఒకే ఎగరవేతలో దొరుసు పడక పోవటానికి సంభావ్యతను కనుక్రోండి.
సాధన:
A, B లు ఇద్దరికి ఒక ఎగరవేతలో దొరుసు పడకపోతే ఫటనను E తీసుకొందాం.
ప్రతి ఎగరవేతలో నాలుగు రకాల అవకాశాలున్నాయి.
i) A కి H రావడం, B కి H రావడం
ii) A కి T రావడం, B కి H రావడం
iii) A కి H రావడం, B కి T రావడం
iv) A కి T రావడం, B కి T రావడం
ఇక్కడ 50 యత్నలు.
కాబట్టి మొత్తం అవకాశాల సంఖ్య 4⁵⁰. పైన పేర్కొన్న నాలుగు సందర్భాల్లో, (i), (ii), (iii) లు మా(తమే ఘటన E కు అనుకూల సందర్భాలు. E కి (iv) అనుకూలం కాదు.
∴ \(\mathrm{P}(\mathrm{E})=\frac{3^{50}}{4^{50}}=\left(\frac{3}{4}\right)^{50}\)

ప్రశ్న 26.
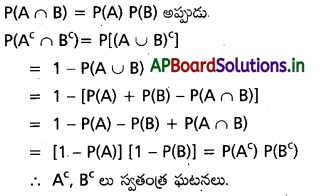
ఒక యాద్చ్ఛిక ప్రయోగంలో A, B లు స్వతంత్ర ఘటనలైతే A^c,B^c లూ రెండూ స్వతంత్ర ఘటలని చూపండి.
సాధన:
A; B స్వతంత్ర ఘటనలు కాబట్టి

ప్రశ్న 27.
ఒక సంచిలో 10 ఒకే మాదిరి బంతులున్నాయి. వీటిలో 4 నీలం రంగువి, 6 ఎర్ర రంగువి. ఒకదాని తరువాత ఒకటి మూడు బంతులను యాధృచ్ఛికంగా ఆ సంచి నుంచి తీస్తే ఆ మూడూ ఎర్రటి బంతులు అయ్యే సంభావ్యతను కనుకొందాం.
సాధన:
మొదట తీసినపుడు అది ఎర్రటి బంతి అడ్యేసంభావ్యత \(\frac{6}{10}\),
రెండోసారి తీసినపుడు ఎర్ర బంతి అమ్యే సంభావ్యత \(\frac{5}{9}\)
మూడోసారి తీసినపుడు ఎర్ర బంతి అమ్యే సంభావ్యత \(\frac{4}{8}\)
కాబట్టి గుణన సిద్ధాంతం నుంచి, కావలసిన సంభావ్యత
\( =\frac{6}{10} \cdot \frac{5}{9} \cdot \frac{4}{8}=\frac{1}{6}\).

ప్రశ్న 28.
ఒక పాత్రలో 7 ఎర్రని, 3 నల్లని బంతులున్నాయి. తీసన ఐంతిని తిరిగి పాత్రలో పెట్టకంండా, రెండు బంతులను తీశారు. ముందుగా తీసన బంతి ఎర్రదని తెలిస్తే, రెండోబంతి ఎర్రనిదయ్యే సంభావ్యతను కనుక్కోండి.
సాధన:
మొదట తీసిన బంతి ఎర్రనిదడ్యే ఘటన R₁ రెండో బంతి ఎళ్రనిదమ్యే ఘటన R₂ అనుకాందాం.

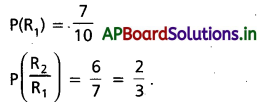
ప్రశ్న 29.
A, B లు రెండు స్వతంత్ర ఘటనలా
P(A)=0.2, P(B)=0.5
(i) \(P\left(\frac{A}{B}\right)\)
(ii) \(\mathrm{P}\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\)
(iii)P(A∩B)
(iv) P(A∪B) లను కనుక్కోండి.
సాధన:
ఇచ్చినది P(A) = 0.2, P(B) = 0.5
మరియు A, B లు రెండు స్వతంత్ర ఘటనలు.

ప్రశ్న 30.
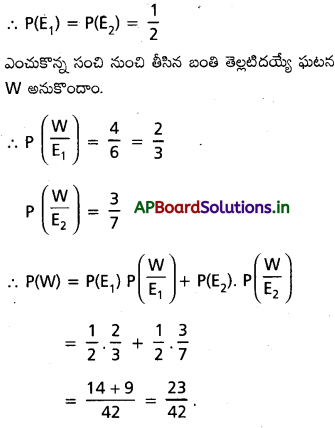
సంచి B₁ లో 4 తెల్లటి, 2 నల్లటి బంతులున్నాయి. సంచి B₂ లో 3 తెల్లటి, 4 నల్లటి బంతులున్నాయి. ఒక సంచిని యాధృచ్ఛికంగా ఎంచుకొని, అందులో నుంచి ఒక బంతిని యాధృచ్ఛికంగా తీస్తే, అది తెల్లటి బంతి అయ్యే సంఖావ్యత ఎంత ?
సాధన:
B₁, B₂ సంచులను ఎంచుకొనే ఘటనలు వరుసగా E₁, E₂ అనుకొందాం.

ప్రశ్న 31.
బేయీ సిద్ధాంతం.
సాధన:
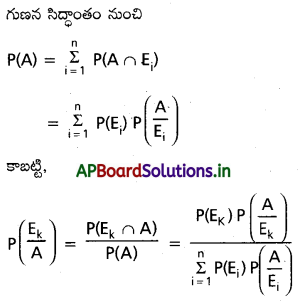
ప్రవచనం : ఒక యాధృచ్ఛిక ప్రయోగంలో E₁, E₂, ……………………. E_n లు n పరస్పర వివరిత, పూర్ణ ఘటనలు: P(E_i )≠ 0,


ప్రశ్న 32.
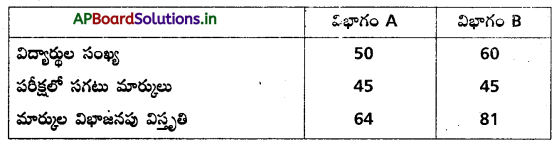
మూడు పెట్టెలు B_{1 ,} B₂, B₃ లలోని ఐంతులు క్రింద వివరించిన రంగులలో ఉన్నాయి.

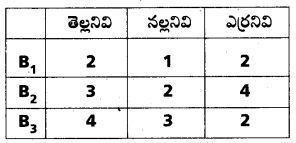
ఒక పాచికను దొర్లించారు. పాచిక పై ముఖంపై 1 లేదా 2 వస్తే B₁ ను ఎన్నుకొంటారు ; 3 లేదా 4 వస్తే B₂ ను ఎన్నుకొంటారు ; 5 లేదా 6 వస్తే B₃ ను ఎన్నుకొంటారు. ఈ విధంగా ఒక పెట్టెను ఎన్నుకొన్నాక, అందులో నుంచి ఒక బంతిని యాదృచ్ఛికంగా ఎన్నుకొన్నారు. అలా ఎన్నుకొన్న బంతి ఎర్రనిదైతే అది పెట్టె B₂ నుంచి వచ్చే సంభావ్త ఎంత ?
సాధన:
పెట్టె B_i ను ఎన్నుకొనే సంభావ్యత P(E_i)(i=1,2,3) అనుకొందాం. అప్పుడు
\(P\left(E_i\right)=\frac{2}{6}=\frac{1}{3} ; i=1,2,3\)
పెట్టె B_i ఎర్రనిదయ్యే సంభావ్యత P(R / E_i) అనుకొంటే

ప్రశ్న 33.
ఒక పార్రలో w తెల్లని b నల్లని బంతులున్నాయి. Q, R అనే ఇద్దరు ఆటగాళ్ళు పాత్ర నుంచి ఒకరి తరువాత ఒకరు, తీసిన బంతిని తిరిగి ఫర్తీ చేస్తూ, బంతులను తోస్తున్నారు. తెల్లటి బంతి ఎవరు ముందుగా తీస్తే వారు గెలిచినట్లు. Q ఆటను వైదలుపెడితే, Q గెలిచే సంభావ్యతను కనుక్కోండి.
సాధన:
తెల్లటి బంతిని తీసే ఘటన W తో, నల్లని బంతిని తీసే ఘటనను B తో సూచించామనుకోండి. అప్పుడు

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 8 విస్తరణ కొలతలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 8 విస్తరణ కొలతలు

ప్రశ్న 1.
అవర్గీకృత దత్తాంశము 6, 7, 10, 12, 13, 4, 12, 16 నకు డుధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.
సాధన:
దత్తాంశానికి అంకమధ్యమం.

ప్రశ్న 2.
అవర్గీకృత దత్తాంశము 6, 7, 10, 12, 13, 4, 12, 16 నకు మధ్యగతం నుంచి మధ్యమ విచలనాన్ని గణించండి.
సాధన:
దత్తబిందువులను పరిమాణం పరంగా ఆరోహణక్రమంలో (వాయగా 4, 6, 7, 10, 12, 12, 13, 16
∴ మధ్యగతం = \(\frac{10+12}{2} = 11\)
పరమ మూల్ల విలువలు
|11-4|, |11-6|, |11-7|, |11-10|, |11-12|, |11-12|, |11-13|, |11-16|
= 7, 5, 4, 1, 1, 1, 2, 5
∴ మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{1}{8}\) (7+5+4+1+1+1+2+5)
= \(\frac{26}{8}\) = 3.25

ప్రశ్న 3.
క్రింది దత్తాంశానికి మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:

ప్రశ్న 4.
క్రింది దత్తాంశానికి మధ్యగతం నుంచి మధ్యమ విచలనం కనుగొనుము.

సాధన:

ప్రశ్న 5.
ఇచ్చిన దత్తాంశానికి మద్యమం నుంచి మధ్యమ విచలనం కనుగొనుము.

సాధన:

ప్రశ్న 6.
క్రింది దత్తాంశానికి, మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:

ప్రశ్న 7.
క్రింది దత్తాయాానికి మధ్యగతం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:

ప్రశ్న 8.
క్రింది దత్తాంశానికి విస్తృతి, (ప్రామాణిక విచలనాలను కనుగొనుము 5,12,3,18,6,8,2,10
సాధన:

ప్రశ్న 9.
క్రింది దత్తాంశానికి విస్తృతి మరియు (ప్రామాణిక విచలనాన్ని కనుగొనుము.

సాధన:

ప్రశ్న 10.
ఈ క్రింది అవిచ్ఛిన్న పౌనఃపున్య విాజనానికి విస్తృతి ప్రామాణిక విచలనాన్ని గణించండి.

సాధన:
ఉహత్మక మధ్యమం A = 65 అనుకొనుము
అపుడు  \(y_i=\frac{x_i-65}{10}\)

ప్రశ్న 11.
ఒక తరగతికి చెందిన రెండు విభాగాలు A, B లలోని విద్యార్థులు, 100 మార్కులకు పెట్టిన ఒక పరీక్షలో క్రింది ఫలితాలను సాధించారు. వీరిలో ఏ విభాగంలోని విద్యార్థులు, వారి ఫలితాలలో ఎక్కువ విచలనాన్ని కలిగి ఉన్నారో కనుగొనుము.

సాధన:
విభాగం – A విద్యార్ధుల మార్కుల విభాజన విస్తృతి σ²₁ = 81
⇒ ప్రామాణిక విచలనం σ₁ =8
విభాగం – B విద్యార్థుల మార్కుల విభాజన విస్తృతి σ²₂ = 81
⇒ σ₂ = 9
రెండు విభాగాలలోని విద్యార్థుల సగటు మార్కులు ఒకటి (అంటి 45) కావున అధిక ప్రామాణిక విచలనం కలిగిన విభాగం ఎక్కువ విచలనాన్ని కలిగి ఉంటుంది.
∴ విభాగం B వారి పనితనం అధిక విచలనాన్ని కలిగి ఉంటుంది.

ప్రశ్న 12.
ఒక సర్వేలో రాబట్టిన రెండు నమూనాల రఫ్రిజిరేటర్లు A, B ల మన్నిక కాలం ఈ క్రింది పట్టికలో ఇవ్వడమైనది. మీరు ఏ నమూనా రిఫ్రిజిరేటరును కొనవచ్చని సూచిస్తారు.

సాధన:
నమూనా A, నమూనా B రి్రిజిరేటర్ల మన్నిక కాలాలు మధ్యమం, విస్తృలిలను కనుక్కొవడానికి పట్టికను నిర్మిద్దాం.

నమూనా B విచలనాంకం నమూనా A విచలనాంకం కంటే తక్కువగా ఉన్నది.
నమూనా B కొనవచ్చునని సూచిస్తాం.

ప్రశ్న 13.
సోపాన విచలన పద్ధతిని ఉపయోగించి, (క్ంిది దత్తాంశానికి మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:
ఉహత్మక మధ్యమం A = 35

ప్రశ్న 14.
ఈ క్రింది పట్టిక, ఒక కర్మాగారంలో పనివాళ్ళ రోజు వారీ జీతాలను తెలుపుతుంది.ఈ పనివాళ్ళ జీతాల ప్రామాణిక విచలనాన్ని, విచలనాంకంను గణనం చేయండి.

సాధన:
తరగతి అంతరాల మధ్యబిందువులు సంఖ్యాపరంగా పెద్దవి కనుక ఈ సమస్యను సోపాన విచలన పద్ధతినుపయోగించి సాధిస్తాము.
ఇక్కడ h=50
ఊహత్మక మధ్యమం A=300
అపుడు \( y_i=\frac{x_i-300}{50}\)

ప్రశ్న 15.
ఒకే రకం పంర్రమకు చెందిన .రండు సంస్థల A, Bలలోని పనివారికి ఇచ్చిన జీతాలను విశ్లేషణ చేసినప్పుడు ఈ క్రింది పట్టికలోని వివరాలు తెలిసాయి.

i) A లేదా B లో ఏ సంస్థ, ఆ పరిశ్రమలోని జీతాలలో ఎక్కువ విచరణ కలిగి ఉంది ?
ii) ఏ సంస్థ ఎక్కువ జీతం బిల్లును కలిగి ఉంది ?
సాధన:
i) ఇచ్చిన σ²_A= 81 ⇒ σ_A= 9
σ²_B = 100 ⇒ σ_B= 10
\(\bar{x}_A\) = 186 మరియు \(\bar{x}_B\) = 175
సంస్థ A జీతాల విభాజనపు విచలనాంకం = \(\frac{\sigma_A}{x_A} \times 100=\frac{9}{186} \times 100=4.84\)
సంస్థ B జీతాల విభాజనపు విచలనాంకం = \(\frac{\sigma_{\mathrm{B}}}{\mathrm{x}_{\mathrm{B}}} \times 100=\frac{10}{175} \times 100=5.71\)
∴ సంస్థ B కి విచలనాంకం, సంస్థ A విచలనాంకం పెద్దది కనుక, వ్యక్తిగత జీతాలకి సంబంధించి, సంస్థ B ఎక్కువ విచలనాన్ని కలిగినదని చెప్పగలం.

ii) సంస్థ A లోని పనివారికి చెల్లించిన మొత్తం జీతాలు= 500 ×186 = 93,000
సంస్థ B లోని పనివారికి చెల్లించిన మొత్తం జీతాలు =600 ×175 = 1,05,000
∴ సంస్థ B కి ఎక్కువ జీతం బిల్లు కలదని చెప్పవచ్చును.

ప్రశ్న 16.
20 పరిశీలనల విస్తృతి 5. (పతి పరిశీలసను 2 చే గుణించినప్పుడు వచ్చే పరిశీలనల విస్తృ)తిని కనుగొనుము.
సాధన:
దత్తపరిశీలనలను x₁, x₂,……………….. x₂₀ వాటి మధ్యమం \(\overline{\bar{x}}\) అనుకొనుము.
దత్తాంశం నుంచి n=20 మరియు విస్తృతతి = 5

∴ ఫలితంగా వచ్బే పరిశీలన విస్త్లృతి = \(\frac{1}{20}\) × 400 = 20 = 2² × 5

ప్రశ్న 17.
పరిశీలన x₁, x₂ ……………………….. x_n లలో (ప్రతిదాన్ని k కి పెంచితే లేదా కలిపితే (k ఒక ధనాత్మక లేదా రుణాత్మక సంఖ్య), వచ్చే పరిశీలనల విస్తృతి ఏమి మారదని చూపండి.
సాధన:
x₁, x₂ ……………………….. x_n ల మధ్యమం x అనుకొందాం.
అప్పుడు వాటి నిస్తృతి \(\sigma_1^2=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \)
ప్రతి పరిశీలనకు ఒక స్థిరరాశి k కలిపితే, వచ్చే కొత్త పరిశీలనలు y_i = x_i + k ………………. (1)

ప్రశ్న 18.
10 ఇన్నింగులలో A, Bఅనే ఇద్దరు క్రికెట్ అటగాళ్ళు స్కోరులు ఈ క్రింద ఇవ్వడమైనది. వీరిలో ఎక్కువ పరుగులు సాధించిన ఆటగాడో, ఎవరు ఎక్కువ నిలకడగల అటగాడో కనుగానుము.

సాధన:

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 7 పాక్షిక భిన్నాలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 7 పాక్షిక భిన్నాలు

ప్రశ్న 1.
\(\frac{5 x+1}{(x+2)(x-1)}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 2.
\(\frac{2 x+3}{5(x+2)(2 x+1)}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 3.
\(\frac{13 x+43}{2 x^2+17 x+30}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 4.
\(\frac{x^2+5 x+7}{(x-3)^3}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 5.
\(\frac{x^2+13 x+15}{(2 x+3)(x+3)^2}\) ను పాక్షిక భిన్నాలు మొత్తంగా (వాయండి.
సాధన:

ప్రశ్న 6.
\(\frac{1}{(x-1)^2(x-2)}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 7.
\(\frac{3 x-18}{x^3(x+3)}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 8.
\(\frac{x-1}{(x+1)(x-2)^2}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 9.
\(\frac{2 x^2+1}{x^3-1}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 10.
\(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}\) ను పాక్షిక భిన్నాలుగా విడగొట్టండి.
సాధన:

ప్రశ్న 11.
\(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}\) ను పాక్షిక భిన్నాలుగా (వాయండి.
సాధన:

ప్రశ్న 12.
\(\frac{x^4+24 x^2+28}{\left(x^2+1\right)^3}\) ను పాక్షిక భిన్నాలుగా (వాయండి.
సాధన:

ప్రశ్న 13.
\(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) ను పాక్షిక భిన్నాలుగా (వాయండి.
సాధన:

ప్రశ్న 14.
\(\frac{x^3}{(2 x-1)(x+2)(x-3)}\) ను పాక్షిక భిన్నాలుగా (వాయండి.
సాధన:

ప్రశ్న 15.
\(\frac{x^4}{(x-1)(x-2)}\) ను పాక్షిక భిన్నాలుగా (వాయండి.
సాధన:

ప్రశ్న 16.
\(\frac{3 x}{(x-2)(x+1)}\) ను x ఘాతకేణణిగా విస్తరించ గలిగే అంతరాన్ని తెలుపుతూ x⁴ గుణకాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 17.
\(\frac{x}{(x-1)^2(x-2)}\) ను x ఘాతకేణణిగా విస్తరించ గలిగే  ప్రదేశాన్ని తెలుపుతూ, xⁿ గుణకాన్ని కనుగొనుము.
సాధన:

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 6 ద్విపద సిద్ధాంతం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 6 ద్విపద సిద్ధాంతం

ప్రశ్న 1.
(2 a+3b)⁶ మొక్క విస్తరణను (వాయండి.
సాధన:

ప్రశ్న 2.
(3 x-4 y)⁷ విస్తరణలో 5వ పదం కనుక్కోండి.
సాధన:

ప్రశ్న 3.
(2 a+5 b)⁸ విస్తరణలో చివరి నుంచి 4వ పదం కనుక్హోండ.
సాధన:
దత్త విస్తరణలో 9 పదాలుంటాయి. కనుక చివరినుంచి 4వ పదం మొదటినుంచి లెక్కిస్తే 6వ పదం అవుతుంది.

ప్రశ్న 4.
క్రింది విస్తరణలో మధ్యపదం కనుక్రోండి.
(i) (3 a-5 b)⁶ (ii) (2 x+3 y)⁷
సాధన:
(i) ఇక్కడ n = 6 (సరిసంఖ్య)

(ii) ఇక్కడ n = 7 (బేసిసంఖ్య)

ప్రశ్న 5.
n ఒక ధన హూ్్ణాంకం అయితే
(i) C₀ + C₁ + C₂ +………………… + C_n = 2ⁿ

(ii) n సరిపూర్ణాంకం అయితే
(a) C₀ + C₂ + C₄ +………………… + C_n = 2^n-1
b) n బేసి హూర్ణాంకం అయితే C₀ + C₂ + C₄ +………………… + C_n-1 = 2^n-1

(iii)
(a) n సరిహ్ణాంకం అయితే C₁ + C₃ + C₅ +………………… + C_n-1 = 2^n-1
(b) n బేసి పూర్ణాంకం అయితే C₁ + C₃ + C₅ +………………… + C_n = 2^n-1
సాధన:

ప్రశ్న 6.
n ధన పూర్ణాంకం అయితే C₀ + 3.C₃ + 5.C₂ +………………… +(2n +1) . C_n = (2n + 2) = 2^n-1 అని చూపండి.
సాధన:

ప్రశ్న 7.
x= \(\frac{2}{3}\) అయినప్పుడు (1 – 5x)¹² విస్తరణలో సంఖ్యాపరంగా గిష్ఠపదం కనుక్కోండి.
సాధన:
ఇక్కడ n=12 మరియు X=-5x

ప్రశ్న 8.
\(x=\frac{3}{4}, y=\frac{2}{7}\), n=17 అయనప్పు (3 x-5 y)ⁿ విస్తరణలో సంఖ్యాపరంగా గరిష్రపదం కనుక్కోండి.
సాధన:
దత్తాంశం\(x=\frac{3}{4}, y=\frac{2}{7}\) మరియు n=17

ప్రశ్న 9.
కింది పదాల విస్తరణలో గరిష్య ద్విపద గుణకం (గుణకాలు) కనుక్కోండి.
(i) (1+x)¹⁹
(ii) (1+x)²⁴
సాధన:
(i) n=19 బేసి పూర్ణాంకం కనుక గరిష్ట గుణకాలు

(ii) n=24 సరి పూర్ణాంకం కనుక (1+x)²⁴ లో గరిష్ఠ ద్విపద గుణకం
\(={ }^n C_{\left(\frac{n}{2}\right)} \text { (i.e.) }{ }^{24} C_{12}\)

ప్రశ్న 10.
(1+x)²² విస్తరణలో గరిష్ఠ ద్విపద గుణకం ²²C_r అయితే ¹³C_r విలువ కనుక్కోండి
సాధన:
n = 22 సరీసంఖ్య. కనుక ఒకే గరిష్ఠ గుణకం ఉంటుంది.

ప్రశ్న 11.
\(\left(\frac{4}{x^3}+\frac{x^2}{2}\right)^{14}\) విస్తరణలో 7వ పదం కనుక్కోండి.
సాధన:

ప్రశ్న 12.
\(\left(x^{-2 / 3}-\frac{3}{x^2}\right)^8\) విస్తరణలో చివరి నుండి 3వ పదం కనుక్కోండి.
సాధన:

ప్రశ్న 13.
\(\left(2 x^2-\frac{1}{x}\right)^{20}\) విస్తరణలో x⁹, x¹⁰ ల గుణకాలు కనుక్కోండి.
సాధన:

ప్రశ్న 14.
\(\left(\sqrt{\frac{x}{3}}+\frac{3}{2 x^{-2}}\right)^{10}\) విస్తరణలో x పై ఆధారపడని పదం (స్థిర పదం) కనుక్కోండి.
సాధన:

ప్రశ్న 15.
\(\left(a x^2+\frac{1}{b x}\right)^{11}\) విస్తరణలో x¹⁰ గుణకం \(\left(a x-\frac{1}{b x^2}\right)^{11}\) విస్తరణలో x^-10 గుణకం సమానమైతే; a, b ల మధ్య సంబంధం కనుక్కోండి. (ఇక్కడ a, b లు వాస్తవ సంఖ్యలు)
సాధన:

ప్రశ్న 16.
\(\left(x^2-\frac{1}{2 x}\right)^{20}\) విస్తరణలో T_k మధ్యపదం అయితే  T_k+3
సాధన:

ప్రశ్న 17.
(1+x)¹⁸ విస్తరణలో (2 r+4),(r-2) పదాల గుణకాలు సమానం అయితే r విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 18.
‘n’ ధన హార్ణాంకం అయితే 2. C₀ + 7.C₁ + 12.C₂ +………………… +(5n +2) C_n = (5n + 4) = 2^n-1 అని చూపండి.
సాధన:

ప్రశ్న 19.
(i) \(C_0+3 \cdot c_1+3^2 \cdot C_2+\ldots \ldots+3^n \cdot C_n=4^n\)
(ii) \(\frac{C_1}{C_0}+2 \cdot \frac{C_2}{C_1}+3 \cdot \frac{C_3}{C_2}+\ldots . .+n \cdot \frac{C_n}{C_{n-1}}=\frac{n(n+1)}{2}\) అని నిరాపించండి.
సాధన:


ప్రశ్న 20.
n = 0,1,2,3, …………………… 0

సాధన:

ప్రశ్న 21.
3.C₀ + 7.C²₁ + 11.C²₂ +………………… + (4n +2) C²_n = (2n + 3) = ²ⁿC_n ఆనిచూపండి.
సాధన:

ప్రశ్న 22.
i) x= \(\frac{11}{8}\) యయనపుడ (2+3x)¹⁰ విస్తరణలో సంఖ్యాపరంగా గరిష్ఠ పదాన్ని కనుక్కోండి.
సాధన:

ii) x=8, y=3 అయినపుడు (3 x-4 y)¹⁴ విస్తరణలో సంఖ్యా పరంగా గరిష్డ పదాలను కనుక్కోండి.
సాధన:

ప్రశ్న 23.
n ఒక ధన హార్ణాంకం అయితే 6²ⁿ-35 n-1 ను 1225 నిశ్ళేషంగా భాగిస్తుందని చూపండి.
సాధన:

ప్రశ్న 24.
n ఒక ధన హూర్ణాంకం అయితే \((7+4 \sqrt{3})^n\) సంఖ్యకు హార్ణాంక భాగం, భిన్న భాగాలు వరుసగా I, F అయితే
(i) I ఒక బేసి హార్ణాంకం
(ii) (I+F) (1 – F) = 1 అని చూపండ
సాధన:

ప్రశ్న 25.
(3+2 x+x²)⁶ విస్తరణలో x⁶ గుణకాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 26.
n ధన పూర్ణాంకం అయిన \(C_0+\frac{C_1}{2}+\frac{C_2}{3}+\ldots \ldots +\frac{C_n}{n+1}=\frac{2^{n+1}-1}{n+1}\) అని చూపండి.
సాధన:

ప్రశ్న 27.
n ఒక ధన హార్ణాంకం మరియు x ఏదేని శూన్యేతర వాస్తవ సంఖ్య అయిన,\(c_0+c_1 \frac{x}{2}+c_2 \cdot \frac{x^2}{3}+ C_3 \cdot \frac{x^3}{4}+\ldots . .+C_n \cdot \frac{x^n}{n+1}=\frac{(1+x)^{n+1}-1}{(n+1) x}\) అని నిరూపించండి.
సాధన:

ప్రశ్న 28.

సాధన:

ప్రశ్న 29.
క్రింది పదాలకు ద్విపద విస్తరణలు వ్యవస్థితం చేసే x ల సమితి E కనుక్కోండి.
(i) (3-4 x)^(3/4)
(ii) (2+5 x)^-1/2
(iii) (7-4 x)^-5
(iv) (4+9 x)^(-2/3)
(v) (a+b x)^r
సాధన:

ప్రశ్న 30.
క్రింద సూచించిన పదాలను కనుక్కోండి.
(i) \(\left(2+\frac{x}{3}\right)^{-5}\) విస్తరణలో 9వ పడం
(ii) \(\left(1-\frac{3 x}{4}\right)^{4 / 5}\) విస్తరణలో 10వ పడం
(iii) \(\left(1-\frac{5 x}{2}\right)^{-3 / 5}\) విస్తరణలో 8వ పడం
(iv) \(\left(3+\frac{2 x}{3}\right)^{3 / 2}\) విస్తరణలో 6వ పడం

(i) \(\left(2+\frac{x}{3}\right)^{-5}\) విస్తరణలో 9వ పడం
సాధన:

(ii) \(\left(1-\frac{3 x}{4}\right)^{4 / 5}\) విస్తరణలో 10వ పడం
సాధన:

(iii) \(\left(1-\frac{5 x}{2}\right)^{-3 / 5}\) విస్తరణలో 8వ పడం
సాధన:

(iv) \(\left(3+\frac{2 x}{3}\right)^{3 / 2}\) విస్తరణలో 6వ పడం
సాధన:

ప్రశ్న 31.
క్రింది విస్తరణలో మొదటి పదాలు వ్రాయండి.
(i) \(\left(1+\frac{x}{2}\right)^{-5}\)
(ii) (3 + 4x)^-2/3
(iii) (4 –  5x)^-1/2

(i) \(\left(1+\frac{x}{2}\right)^{-5}\)
సాధన:

(ii) (3 + 4x)^-2/3

సాధన:

(iii) (4 –  5x)^-1/2

సాధన:

ప్రశ్న 32.
క్రింది ద్విపద విస్తరణలో సాధారణ పదం కనుక్కోండి.
(i) \(\left(3+\frac{x}{2}\right)^{-2 / 3}\)
(ii) \(\left(2+\frac{3 x}{4}\right)^{4 / 5}\)
(iii) (1 – 4x)^-3
(iv) ( 2- 3x)^-2/3

(i) \(\left(3+\frac{x}{2}\right)^{-2 / 3}\)
సాధన:

(ii) \(\left(2+\frac{3 x}{4}\right)^{4 / 5}\)
సాధన:

(iii) (1 – 4x)^-3
సాధన:

(iv) ( 2- 3x)^-2/3
సాధన:

ప్రశ్న 33.
\(\frac{1+3 x}{(1-4 x)^4}\) విస్తరణలో x¹² గుణకం కనుక్కోండి.
సాధన:

ప్రశ్న 34.
(1 – 3x)^-2/5 విస్తరణలో x⁶ గుణకాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 35.
క్రింది ఆనంతశేణ మొత్తం కనుక్కోండి.
\(1+\frac{2}{3} \cdot \frac{1}{2}+\frac{2.5}{3.6}\left(\frac{1}{2}\right)^2+\frac{2.5 .8}{3.6 .9}\left(\frac{1}{2}\right)^3+\ldots \ldots \infty\)
సాధన:

ప్రశ్న 36.
క్రింది ఆనంతశేణ మొత్తం కనుక్కోండి.
\(\frac{3.5}{5.10}+\frac{3.5 .7}{5.10 .15}+\frac{3.5 .7 .9}{5.10 .15 .20}+\ldots \ldots \infty\)
సాధన:

ప్రశ్న 37.
\(x=\frac{1}{5}+\frac{1.3}{5 \cdot 10}+\frac{1 \cdot 3.5}{5 \cdot 10.15}+\ldots \ldots \infty\) అయితే  3x² + 6x విలువ కనుక్కోండి
సాధన:

ప్రశ్న 38.
(i) \(\frac{1}{\sqrt[3]{999}}\)
(ii) (627)^1/4 మొక్క ఉజ్ణాయింప విలువలా దశాంశాలకు సవరించి కనుక్కోండి.
సాధన:

ప్రశ్న 39.
x³ ఆపై  x ఘాతాలను ఉపేక్షించేంతగా |x| స్వల్పమైతే \(\frac{(4-7 x)^{1 / 2}}{(3+5 x)^3}\) ఉజ్ణాయింపు విలువను కనుక్కోండి.
సాధన:

ప్రశ్న 40.
\(\sqrt[6]{63}\) మొక్క ఉజ్జాయింపు విలువను దశాంశాలకు సవరించి కనుక్కోండి.
సాధన:

ప్రశ్న 41.
x³ ఆపై  x ఘాతాలను ఉపేక్షించేంతగా |x| స్వల్పమైతే \(\frac{\left(1+\frac{3 x}{2}\right)^{-4}(8+9 x)^{1 / 3}}{(1+2 x)^2}\) ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 42.
x⁴ ఆపై  x ఘాతాలను వదిలివేసేంతగా |x| చిన్నదయితే \(\sqrt[4]{x^2+81}-\sqrt[4]{x^2+16}\) ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 43.
x, y లు ధన వాస్తవ సంఖ్యలు. yతో పోలిస్తే విలావ చాలా చిన్నదయతే, \(\left(\frac{y}{y+x}\right)^{3 / 4}-\left(\frac{y}{y+x}\right)^{4 / 5}\) ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 44.
\(5 \sqrt{5} \text { ను } \frac{4}{5}\) యొక్క ఆరోహణ ఘాతాలలో విస్తరించి ప్రాయండి.
సాధన:

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 5 ప్రస్తారాలు-సంయోగాలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 5 ప్రస్తారాలు-సంయోగాలు

ప్రశ్న 1.
ⁿP₄  = 1680 అయిన n విలువ ఎంత ?
సాధన:
ⁿp₄  = 1680
= n(n – 1) (n – 2) (n – 3) = 8 x 7 x 6 x 5
∴ n = 8

ప్రశ్న 2.
¹²P_r  = 1320 అయితే r విలువ కనుక్కోండి.
సాధన:
¹²P_r  = 1320
= 10 x 132 = 10 x 11 x 12
= 12 x 11 x 10 = ¹²P₃
∴ r = 3.

ప్రశ్న 3.
⁽ⁿ⁺¹⁾P₅ : ⁿP₅ = 3:2 అయితే n విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 4.
⁵⁶P_(r+6) : ⁵⁴P_(r+3) = 30800 : 1 అయితే r విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 5.
9 గణితశాస్త్ర పరీక్షాపత్రాలను, వాటిలో (శేష్ఠమయినది (the best), హీనమైనది (the worst)
(i) కలిసి ఉండేట్లుగా
(ii) వేరు వేరుగా ఉండేట్లు ఎన్ని విధాలుగా అమర్చవచ్చు.
సాధన:
(i) ఈ రెండు రకాలైన పేపర్లను ఒక యూనిట్గా భావిస్తే మనకి మొత్తం 9-2+1=7+1=8 పేపర్లు ఉన్నాయి. వీటిని 8! విధాలుగా అమర్చవచ్చు, ఆ రెండు పేపర్లను 2! విధాలుగా వాటిలో వాటిని అమర్చవచ్చు. కనుక కావలసిన అమరికల సంఖ్య (ఆ రెండు పేపర్లు కలిసి ఉండేట్లుగా) 8! 2!.

ii) మొత్తం 9 పేపర్లను అమర్చే విధానాలు 9!.వీటిలో శేేష్రమైనది, హీనమైనది కలిసి ఉండేట్లుగా అమర్చే విధానాలు 8! 2!. కనుక, రెండు గణితశాస్త్ర పేపర్లు వేరు వేరుగా ఉండేట్లుగా అమర్చే విధానాలు
9! – 8! 2! (9-2)=8 ! × 7

ప్రశ్న 6.
ఆరుగురు బాలురు, ఆరుగురు బాలికలను ఒక వరసలో అమర్చగలిగే విధానాలెన్ని ? వాటిలో ఎన్నిటిలో
(i) బాలికలందరూ కలిసి ఉంటారు.
(ii) ఏ ఇద్దరు బాలికలు పక్క పక్కన రాకుండా ఉంటారు.
(iii) బాలారం, బాలికలా ఒకరిశరువాత ఒకరంగా ఉంటారా.
సాధన:
ఆరుగురు బాలురు, ఆరుగురు బాలికలు కలిపి మొత్తం 12 మంది వ్యక్తులున్నారు. కనుక వీరిని ఒక వరసలో అమర్చ గలిగే విధానాలు 12 !

(i) ఆరుగురు బాలికలను ఒక యూనిట్గా భావిస్తే, అప్పుడు ఆరుగురు బాలురు + ఒక బాలికల యూనిట్ ఉంటాయి. వాటిని ఒక వరసలో 7! విధాలుగా అమర్చవచ్చు. ఇప్పుడు, ఆరుగురు బాలికలను వారిలో వారిని 6! విధాలుగా అమర్చవచ్చు. కనుక ఆరుగురు బాలికలు కలిసి ఉండేలా అమర్చగలిగే విధానాలు.
=7 ! × 6 !

(ii) ముందుగా ఆరుగురు బాలురను ఒక వరసలో 6 ! విధాలుగా అమర్చవచ్చు. అప్పుడు బాలుర మధ్యలో మొదట, చివర మొత్తం.

7 ఖాళీలుంటాయి (పైన ఖాళీలను x తో సూచించాం).
ఈ 7 ఖాళీలలో ఆరుగురు బాలికలను అమర్చే విధానాలు ⁷P₆ కనుక ఏ ఇద్దరు బాలికలు పక్క పక్కన రాకుండా అమర్చే విధానాలు. 6! ×⁷P₆ =7.6 !. 6 !

(iii) వరస బాలుడు లేదా బాలికతో మొదలు కావచ్చు అంటే అవి 2 విధాలు ఉదాహరణకు బాలుడితో మొదలయిందను కొందాం. అప్పుడు బాలురు, బాలికలు ఏకాంతంగా రావాలంటే బాలురను బేసిసంఖ్య గల స్థానాల్లో బాలికలను సరిసంఖ్య గల స్థానాల్లో అమర్చాలి. కనుక ఆరుగురు బాలురను సరి సంఖ్యగల 6 స్థానాలలో అమర్చే విధానాలు = 6!
ఆరుగురు బాలికలను బేసి సంఖ్య గల 6 స్థానాలలో అమర్చే విధానాలు =6 !
కనుక కావలసిన ప్రస్తారాల సంఖ్య =2 ×6! × 6!

ప్రశ్న 7.
MIRACLE పదంలోని అక్షరాలను ఉపయోగించి 4 ఆక్షరాల పదాలు ఎన్ని తయారు చేయవచ్చు? వాటిలో ఎన్ని పదాలు
(i) అచ్చుతో మొదలవుతాయి ?
(ii) అచ్చుతో మొదలయి, అచ్చులో అంతమవుతాయి ?
(iii) హల్లుతో అంతమవుతాయి.
సాధన:
MIRACLE పదంలో 7 అక్షరాలున్నాయి. కనుక వీటిని ఉపయోగించి ఏర్పరిచే 4 అక్షరాల పదాల సంఖ్ర
⁷P₄ = 7 × 6 × 5 × 4 = 840
ఇప్పుడు నాలుగు ఖాళీ స్థానాలు తీసుకుందాం.

(i) మొదటి స్థానాన్ని ఇచ్చిన పదంలోని 3 అచ్చులలో {I, A,E} ఏదో ఒకదానితో 3 విధాలుగా నింపవచ్చు మిగిలిన 3 స్థానాలను మిగిలిన 6 అక్షరాలతో నింపే విధానాల సంఖ్య
=⁶P₃  =6 × 5 × 4 = 120
కనుక అచ్చుతో మొదలయ్యే 4 అక్షరాల పదాల సంఖ్య
=3 × 120 = 360

(ii) ముందుగా మొదటి, చివరి స్థానాలను అచ్చులతో { I, A,E) నింపే విధానాల సంఖ్య ³P₂ 2= 3 × 2 = 6
మిగిలిన 2 స్థానాలను మిగిలిన 5 అక్షరాలలో నింపే విదానాల సంఖ్య ⁵P₂ = 5 × 4 = 20 కనుక అచ్చుతో మొదలయ్యి అచ్చుతో అంతమయ్యే 4 అక్షరాల పదాలు = 6 × 20=120

(iii) చివరి స్థానాన్ని 4 హల్లులలో ఒక దానితో నింపే విధానాలు = ⁴P₁ =4
మిగిలిన 3 స్థానాలు విగిలిన 6 అక్షరాలతో నింపే విధానాల సంఖ్య =  ⁶P₃=6 × 5 × 4=120
కనుక హల్లుతో అంతమయ్యే 4 అక్షరాల పదాల సంఖ్య
= 4 × 120 = 480

ప్రశ్న 8.
PICTURE అనే పదంలోని అక్షాలన్నింటినీ ఉపహాగించి ఏర్పరిచే ప్రస్తారాలలో ఎన్నిటిలో
(i) అచ్చులన్నీ కలిసి ఉంటాయి
(ii) ఏ రండు అచ్చులు పక్క పక్కన లేకుండా ఉంటాయి?
(iii) అచ్చులు, హల్లులు సాపేక్ష స్థానాలు మారకుండా ఉంటాయి.
సాధన:
పదంలో 3 అచ్చులు (I, U, E), 4 హల్లులు (P, C, T, R) ఉన్నాయి.

(i) 3 అచ్చును ఒక యూనిట్గా భావిస్తే, 4 హల్లులు + 1 యూనిట్ అచ్చులు మొత్తం 5 అవుతాయి. ఈ ఐదింటిని 5 ! విధాలుగా అమర్చవచ్చు. ఇప్పుడు 3 అచ్చులను వాటిలో వాటిని 3! విధాలుగా అమర్చవచ్చు. కనుక ప్రాథమిక సూత్రం ప్రకారం, ఈ రెండు పనులను 5 ! × 3 ! విధాలుగా చేయవచ్చు. కనుక మూడు అచ్చులు కอిసి వుండే ప్రస్తారాల సంఖ్య
= 5! × 3 ! = 120 × 6 = 720

(ii) ముందుగా 4 హల్లులను.ఒక వరసలో 4 ! విధాలుగా అమర్చవచ్చు. ఇప్పుడు హల్లుల మధ్యలో మూడు, మొదట, చివర మొత్తం 5 ఖాళీ స్థానాలు ఉంటాయి వీటిని x తో సూచిందాం

ఈ 5 ఖాళీలలో 3 అచ్చులను ⁵P₃ విధాలుగా అమర్చవచ్చు
కనుక ఏ రెండు అచ్చులు పక్క పక్కన రాకుండా అమర్చే
విధానాలు
= 4! × ⁵P₃
=24 × 5 × 4 × 3 = 1440

(iii) మూడు హల్లలను వాటి సాపేక్ష స్థానాలలో 3 ! విధాలుగా అమర్చవచ్చు. అదే విధంగా 4 అచ్చులను వాటి సాపేక్ష స్థానాలలో 4! విధాలుగా అమర్చవచ్చు.

కనుక కావలసిన ప్రస్తారాలు సంఖ్య 3!  4! = 144

ప్రశ్న 9.
PRISON పదంలోని అక్షరాలతో ఏర్పడే 6 అక్షరాల పదాలన్నింటినీ నిఘంటువులోని క్రమంలో అమరిస్తే, (పునరావృతం లేకండా) ఆ (క్రమంలో దాని మొక్క కోటిని కనుక్కోండి.
సాధన:
దత్త పదంలోని అక్షరాల నిఘంటువు క్రమం
I  N  O P R S
నిఘంటువులో ముందుగా I తో మొదలయ్యే పదాలన్నీ వస్తాయి. ఆతరువాత N తో మొదలయ్యేవి, O తో మొదలయ్యే పదాలు వస్తాయి. వీటి తరువాత P తో మొదలయ్యే పదాలు వస్తాయి. వీటిలోనే మనకు కాలసిన పదం PRISON ఉంది. కనుక వీటి నిఘంటువు క్రమాన్ని గమనిస్తే వీటిలో ముందుగా PI తో మొదలయ్యే, పదాలు తదుపరి PN తో, ఆ తరువాత PR తో మొదలయ్యేవి వస్తాయి. ఈ విధంగా PRISON అనే పదం వచ్చేంత వరకు లెక్కించాలి.

ముందుగా I తో మొదలయ్యే పదాల సంఖ్యను గణించ డానికి I ని మొదటి స్థానంలో ఉంచి మిగిలిన 5 అక్షరాలను రకరకాలుగా అమర్చాలి. ఈ రకమైన అమరికలు 5! ఉంటాయి. అంటే I మొదటి అక్షరంగా గల పదాల సంఖ్య 5! అన్నమాట, ఈ విధంగా PRISON అనే పదం వచ్చే వరకు కింది విధంగా గణిస్తాం.

కనుక PRISON అనే పదం కోటి
= 3 x 5! +3 x 4 + 2 x 2! +1+1
= 360 + 72 + 4 + 1 + 1 = 438

ప్రశ్న 10.
2,3,5,6,8 అంకెలనుపయోగించి పునరావృతం లేకుండా ఎన్ని 4 అంకెల సంఖ్లలు తయారు చేయవచ్చు? వాటిలో ఎన్ని
(i) 2
(ii) 3
(iii) 4
(iv) 5
(v) 25
సాధన:
2, 3, 5, 6, 8 అనే.5 అంకెలనుపయోగించి తయారు చేయగల 4 అంకెల సంఖ్లలు ⁵P₄ = 120.

(i) 2తో భాగించబడేవి : ఒక సంఖ్య 2తో భాగించబడటానికి దాని చివర (ఒకట్ల) స్థానంలో సరిసంఖ్య ఉండాలి. అంటే ఈ స్థానాన్ని 2 లేదా 6 లేదా 8 తో నింపవచ్చు. ఇప్పుడు మిగిలిన 3 స్థానాలను.

మిగిలిన 4 అంకెలతో ⁴P₃ విధాలుగా నింపవచ్చు. కనుక =3 x ⁴P₃ = 3 x 24=72

(ii) 3 తో భాగించబడేవి : ఒక సంఖ్య 3 తో భాగించబడటానికి ఆ సంఖ్యలోని అంకెల మొత్తం 3 తో భాగించబడాలి. మనకు ఇచ్చిన 5 అంకెల మొత్తం 24 కనుక వీటి నుంచి 4 అంకెలను ఆ అంకెల మొత్తం 3 తో భాగించబడే విధంగా 2 రకాలుగా ఎంచుకోవచ్చు,
(i) 2,5,6,8
(ii) 2,3,5,8

పైన చెప్పిన రెండు సందర్భాలలో ప్రతిసారి 4 అంకెలతో తయారు చేయగల 4 అంకెల సంఖ్యల సంఖ్య 4 ! (ఇవి అన్నీ 3 తో భాగించబడతాయి). కనుక 3 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్య
2 × (4!)=2 × 24 = 48

(iii) 4 తో భాగించణడేవి : ఒక సంఖ్య 4 తో భాగించ బడాలంటే చివరి రెండు స్థానాల్లో అంటే పదులు, ఒకట్ల స్థానాల్లో ఉన్న రెండంకెల సంఖ్య 4తో భాగించబడాలి.
కనుక ఈ రెండు స్థానాలను 28,32,36,52,56 అనే సంఖ్యలతో నింపాలి.

అంటీ 5 విధాలుగా ఈ రెండు స్థానాలు నింపవచ్చు. ఇప్పుడు మిగిలిన రెండు స్థానాలను 3 అంకెలతో ³P₂ విధాలుగా సంఖ్.
= 5 × ³P₂=30.

(iv) 5 తో భాగించణడేవి : ఒక సంఖ్య 5 తో భాగించ బడాలంటే చివరి (ఒకట్ల) స్థానంలో 5 ఉండాలి. (‘0’ కూడా ఉండవచ్చు కాని దత్త అంకెలలో ‘0’ లేదు). కనుక ఒకట్ల స్థానంలో5ఉంచితే మిగిలిన 3 స్థానాలను మిగిలిన 4 అంకెలతో ⁴P₃ విధాలుగా నింపవచ్చు. కనుక 5 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్ల ⁴P₃ =24.

(v) 25 తో భాగించణడేవి : ఒక సంఖ్య 25 తో భాగించ బడాలంటే చివరి రెండు స్థానాలను 25 మాత్రమే నింపాలి (50 లేదా 00తో కూడా నింపవచ్చు కాని .దత్త అంకెలలో ‘ 0 ‘ లేదు) అంటే ఈ స్థానాలు ఒక విధంగా మాత్రమే నింపవచ్చు. ఇప్పుడు మిగిలిన 2 స్థానాలను మిగిలిన 3 అంకెలతో ³P₂ విధాలుగా నింపవచ్చు.

ప్రశ్న 11.
1, 3,5,7,9 అంకెలను ఉపయోగించి ఏర్పరచగల 4 అంకెల సంఖ్యల మొత్తం కనుక్కోండి.
సాధన:
1,3,5,7,9 అనే 5 అంకెలతో ఏర్పరచగల 4 అంకెల సంఖ్ల సంఖ్  ⁵P₄ = 120.
ఇప్పుడు ఈ 120 సంఖ్యల మొత్తం కనుక్కోవాలి. ముందుగా మనం ఈ 120 సంఖ్యల ఒకట్ల స్థానంలోని అంకెల మొత్తం కనుక్కొందాం. ఒకట్ల స్థానంలో 1 ఉంచితే మిగిలిన 3 స్థానాలను మిగిలిన 4 అంకెలతో  ⁴P₃  విధాలుగా నింపవచ్చు.

అంటే పైన చెప్పివ 120 నాలుగంకెల సంఖ్యలలో ⁴P₃ సంఖ్య ఒకట్ల స్థానంలో 1 వస్తుంది. ఇదేవిధంగా 3, 5, 7, 9 అంకెలు ఒక్కొక్కటి ⁴P₃ సార్లు ఒకట్ల స్థానంలో వస్తాయి. ఈ అంకెలన్నీ కలిపితే మనకు 120 సంఖ్య ఒకట్ల స్థానంలోని మొత్తం.
= ⁴P₃ x 1 + ⁴P₃ x 3 + ⁴P₃  x 5
= ⁴P₃ x 7 + ⁴P₃ x 9
= ⁴P₃ (1+3+5+7+9)
= ⁴P₃  (25)
ఇదే విధంగా ఈ 120 సంఖ్యల పదుల స్థానంలో కూడా పైన చెప్పిన అంకెలు మాత్రమే వస్తాయి. కనుక పదుల స్థానంలోని అంకెలు మొత్తం కూడా ⁴P₃ x 25 కాని ఇది పదుల స్థానంలోని మొత్తం కనుక దాని విలువ ⁴P₃ x 25 x 10. ఇలాగే వందల స్థానంలోని అంకెల మొత్తం విలువ ⁴P₃ x 25 x 100  కనుక 1,3,5,7,9 అంకెలనుపయోగించి ఏర్పరిస్తే వచ్చే 4 అంకెల సంఖ్ల మొత్తం.

ప్రశ్న 12.
1,2,5,7,8,9 అంకెలలో ఎన్ని 4 అంకెల సంఖ్యలా సంఖ్యలు ఎన్ని?
సాధన:
1, 2, 5, 7, 8,9 అంకెలతో ఏర్పడే నాలుగు అంకెల సంఖ్యలు ⁴P₂ = 360 ఇప్వుడు మొదటి స్థినాన్ని 9తో, చివరిస్థానాన్ని 2 తో నింపే విధానాల సంఖ్య 1.⁴P₂ = 12.

ప్రశ్న 13.
5 మూలకాలున్న సమితి A నుంచి 7 మూలకాలున్న సమితి B క గల అన్వేక ప్రమేయాల సంఖ్య కనుక్కొండి.
సాధన:
A లోని మొదటి మూలకానికి ప్రతిబింబాన్ని B లోని 7 మూలకాలలో ఏదో ఒక మూలకంగా అంటే 7 విధాలుగా నిర్వచించవచ్చు.A లోని రెండవ మూలకానికి, (ప్రతిబింభాన్ని B లోని మిగిలిన 6 మూలకాలలో ఏదో ఒక మూల కంగా అంటే 6 విధాలుగా మాత్రమే నిర్వచించ గలం.
ఇలా చేసుకుంటూ పోతే A నుంచి B కి గల అన్వేక ప్రమేయాల సంఖ్ల = ⁷P₅
= 7 × 6 × 5 × 4 × 3 = 2,520
గమనిక : సమితి A లోని m మూలకాలు, సమితి B లోని n మూలకాలుంటే A నుంచి B కి నిర్వచించగల అన్వేక (ప్రమేయాల సంఖ్య
= ⁿP_m m ≤ n అయితే
0, m ≤ n అయితే

ప్రశ్న 14.
ఉత్తరాలను వాటికి సంబంధించిన చిరునామాలు ఉన్న 4 కవర్లలో ఏ ఉత్తరమా దానికి సంబంధించిన కవరులోకి ఏోకుండా ఉండేలా, ఒక్కొక్క కవరులో ఒక్కొక్క ఉత్తరం ఉండేలా ఎన్ని విధాలుగా ఆమర్చవచ్చు.
సాధన:
కావలసిన అమరికల సంఖ్య \( = 4 !\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right)\)
= 12 – 4 + 1 = 9

ప్రశ్న 15.
MIXTURE పదంలోని అక్షరాలతో, పునరావృతాన్ని అనుమతించినపడు, ఏర్పరచగల 5 ఆక్షరాల పదాలలో అచ్చుతో మొదలయ్యే పదాలెన్ని?
సాధన:
MIXTURE పదంలో 7 అక్షరాలున్నవి. అందు 3 అచ్చులు (I, U, E), 4హల్లలలు (M, X,T, R)

కనుక మొదటి స్థానాన్ని ఒక అచ్చుతో 3 విధాలుగా నింపవచ్చు. మిగిలిన 4 స్థానాలలో ఒక్కొస్థానాన్ని 7 విధాలుగా నింపవచ్చు. (పునరావృతాన్ని అనుమతించాం కనుక)
∴  అచ్చుతో మొదలయ్యే 5 అక్షరాల పదాలు
= 3 × 7 × 7 × 7 × 7=3 × 7⁴

ప్రశ్న 16.
(a) m మూలకాలాన్న ఒక సమితి A నుండి n మాలకాలున్న సమితి B అన్ని (ప్రమేయాలు నిర్వచించవచ్చు ?
సాధన:
A = {a_1,a_2,………….. a_m}
B = {b_1,b_2,………….. b_m}
గా తీసుకొందాం. ముందుగా a₁ ప్రతిబింబానికి B లో ఒక మూలకం ఎంచుకోవాలి. దీనిని మనం n విధాలుగా ఎంచుకోవాలి. ఈ విధంగా A లో ఉన్న m మూలకాలలో ప్రతి మూలకం యొక్క (పతిబింబాన్ని n విధాలుగా నిర్వబించ వచ్చు. ఒక ప్రమేయాన్ని నిర్వచించినపుడు ఒకటి కన్నా ఎక్కువ మూలకాలకు ఒకే (పతిబింబం ఉండవచ్చు. కనుక A లోని m మూలకాల ప్రతిబింబాలను
n × n × …………….. x n (m సార్లు) = n^m
విధాలుగా నిర్వచించవచ్చు. కనుక A నుండి B కి గల ప్రమేయాల సంఖ్య n^m

(b) n మూలకాలున్న ఒక సమితి A నుంచి 2 మాలకాలున్న సమితి B కు ఎన్ని సంగ్రస్త ప్రమేయాలు నిర్వచించ వచ్చు ?
సాధన:
A = {a_1,a_2,………….. a_n} గా తీసుకొందాం. పై సమస్య ప్రకారం A నుండి B కి గల [ప్రమేయాల సంఖ్య 2ⁿ ఒక ప్రమేయం సంగ్రస్తం కావాలంటే B లోని రెండు మాలకాల x, y లు ప్రమేయం వ్యాప్తిలో ఉండాలి.కనుక (ప్రమేయం సంగ్రస్తం కాకుండా ఉండాలంటే హ్యాప్తిలో x (లేదా y) మాత్రమే ఉండేలా A లోని అన్ని మూలకాల (ప్రతిబింబాలు x (లేదా y) అ ్లేటటట్లు నిర్వచించాలి. ఈ విధమైన ప్రమేయాలు రెండు మాత్రమే ఉంటాయి. కనుక A నుండి B కి నిర్వచించగల 2ⁿ (ప్రేయాల్లో 2 ప్రమేయాలు సంగ్రస్తం కావు. అంటే A సుంచి B కి గల సంగ్రస్త ప్రమేయాల సంఖ్య 2ⁿ– 2.

ప్రశ్న 17.
ప్రావృతాన్ని అనుమతించినప్పుడు 1, 2, 3, 4, 5, 6 అంకెలలో ఏర్పరచగలిగే 4 అంకెల సంఖ్లల సంఖ్యను కనుక్రోండి.
సాధన:
పునరావృతాన్ని అనుమతించినప్పుడు 4 స్థానాలను ఇచ్చిన 6 అంకెలతో నింపే విధానాలు
= 6 × 6 × 6 × 6=6⁴=1,296

ప్రశ్న 18.
పునరావృతాన్ని అనుమతించినప్పుడు 1,2,3,4,5,6 అంకెలతో ఏర్పరిచే 4 అంకెల సంఖ్యలలో ఎన్ని
(i) 2 (ii) 3 తో ఖాగించబడతాయి?
సాధన:
(i) 2 తో భాగించణడే సంఖ్లలు 4 ఖాళీస్థానాలు తీసుకొందాం. ఒక సంఖ్య 2 తో భాగించ బడాలంటే

ఒకట్ల స్థానంలో సరిసంఖ్య ఉండాలి. కనుక ముందుగా ఒకట్ల స్థానాన్ని ఒక సరిసంఖ్య (2 లేదా 4 లేదా 6) తో ‘3’ విధాలుగా నింపవచ్చు. మిగిలిన 3 స్థానాలలో ఒక్కో స్థానాన్ని ఇచ్చిన 6 అంకెలలో దేనితోనైనా 6 విధాలుగా నింపవచ్చు. కనుక 2 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్య
= 3 × 6³=3 × 216 = 648

(ii) 3తో భాగించణడే సంఖ్యలు
మొదటి 3 స్థానాలలో ఒక్కో స్థానాన్ని 6 విధాలుగా, అంటే మొత్తం 6³ విధాలుగా నింపవచ్చు.

ఈ విధంగా మొదటి. మూడు స్థానాలు నింపాక ఒకట్ల స్థానం నింపడానికి 6 వరుస పూర్ణాంకాలున్నాయి. వీటితో ఒకట్ల స్థానాన్ని నింపితే 6 వరుస ధన సంఖ్యలు వస్తాయి. ప్రతి 3 వరుస ధనపూర్ణాంకాల్లో ఖచ్చితంగా ఒక సంఖ్య 3తో భాగింపబడుతుందని మనకు తెలుసు. కనుక పైన చెప్పిన 6 వరుస ధన పూర్ణాంకాల్లో ఖచ్చితంగా 2 మాత్రమే 3 తో భాగించబడతాయి. అంటే ఒకట్ల స్ధానాన్ని 2 విధాలుగా మాత్రమే నింపవచ్చు కనుక 3 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్య.
= 6³ × 2 = 216 × 2 = 432

ప్రశ్న 19.
ఫునరావృతాన్ని అనుమతించినపుడు EXPLAIN పదం లోని అక్షరాలతో మొదట, చివర అచ్చులు ఉండేటట్లు 5 అక్షరాల పదాలు ఎన్ని ఏర్చరచవచ్చు ?
సాధన:
EXPLAIN పదములో 7 అక్షరాలున్నవి అందులో 3 అచ్చులు (A,E,I) లు ఉన్నాయి. కనుక మొదటి, చివరి స్థానాలలోను అచ్చులతో ఒక్కోదాన్ని 3 విధాలుగా నింపవచ్చు. మిగిలిన మూడు స్థానాలలో ఒక్కోదాన్ని ఇచ్చిన పదంలోని 7 అక్షరాలలో ఏదో ఒక అక్షరంతో 7 విధాలుగా నింపవచ్చు.
కనుక మొదటి, చివిరి అచ్చులు ఉండే 5 అక్షరాల పదాల సంఖ్య.
=3 × 7 ×7 ×7 × 3
=9 × 343=3,087

ప్రశ్న 20.
SINGING పదంలోని అక్షరాలను
(i) Iతో మొదలయి, Iతో అంతమయ్యేలా
(ii) రెండు Gలుకలిసి ఉండేలా ఎన్ని విధాలుగా అమర్చవచ్చు ?
(iii) అచ్చులు, హల్లులు సాపేక్ష స్థానాలు మారకుండా ఎన్ని విధాలుగా అమర్చవచ్చు ?
సాధన.
SINGING పదంలో 2I లు, 2G లు, 2Nలు, ఒక S మొత్తం 7 అక్షాాలున్నవి.

(i) ముందుగా మొదటి,చివరి స్థానాలను రెండు Iలతో

నింపితే ఇంకా 5 స్థానాలు, 5 అక్షరాలు ఉంటాయి. కనుక వీటిని అమర్చే విధానాలు \(\frac{5 !}{2 ! 2 !}\) (రెండు N లు)
రెండు G లు ఉన్నాయి. కనుక I లు రెండూ ఒకే రకంగా ఉన్నందువల్ల వాటిలో వాటిని ఒక రకంగా మాత్రమే మార్చగలం.
కనుక కావలసిన ప్రస్తారాల సంఖ్య \(\frac{5 !}{2 ! ~ 2 !}\) = 30

(ii) రెండు ‘G’ లను.ఒక యూనిట్ గా భావిస్తే, విగిలిన 5 అక్షరాలు + 1 యూనిట్= 6 వీటిలో 2I లు, 2N లు ఉన్నాయి. కనుక
ఈ 6 అక్షరాలను అమర్చే విధానాలు \(\frac{6 !}{2 ! 2 !}=\frac{720}{2 \times 2}=180\)
ఇప్పుడు ఒక యూనిట్ లో ఉన్న G లను వాటిలో
కనుక రెండు G లు కలసి ఉండే పదాల సంఖ్ల = 180

(iii) SINGING పదంలో రెండు అచ్చులు (1,1). 5 హల్లులు (రెండు nలు, రెండు Gలు ఒక S) ఉన్నాయి. రెండు అచ్చులను వాటిలో వాటిని అమర్జే విధానాలు \(=\frac{2 !}{2 !}\) 1.5 హల్లులను వాటిలో వాటిని అమర్చే విధానాలు \(\frac{5 !}{2 ! 2 !}\) = 30
C V C C V C C (ఇక్కడ V ఒక అచ్చుని, C ఒక హల్లుని
∴ కావలసిన ప్రస్తారాల సంఖ్య = 130 x 30=30

ప్రశ్న 21.
a⁴, b³, c⁵ పదంలోని అక్షరాలను విస్తరించి రాసి వాటిని అమర్చడం ద్వారా వచ్చే (ప్రస్తారాల సంఖ్లను కనుక్రోండి.
సాధన:
a⁴, b³, c⁵ విస్తరించి రాస్తే
aaaa bbb ccccc
దీనిలో 12 అక్షరాలున్నాయి. వాటిలో 4 ‘a’ లు, 3 ‘b’ లు, 5 ‘c’ లు. కనుక వాటిని అమర్చడం ద్వారా వచ్చే (ప్రస్తారాల సంఖ్య
\(\frac{12 !}{4 ! 3 ! 5 !}\)

ప్రశ్న 22.
1,1,2,2,3 అనే అంకెలతో ఏర్పర్గగ 5 అంకెల సంఖ్లెన్ని ? వీటిలో సరిసంఖ్యలన్ని ?
సాధన:
1, 1, 2, 2, 3 అనే 5 అంకెలలో రెండు ‘1’ లు, రెండు ‘2’ లు ఉన్నాయి. కనుక వీటి నుంచి ఏర్పరచగల 5 అంకెల
సంఖ్య = \(\frac{5 !}{2 ! 2 !}\) = 30
ఇప్పుడు సరి సంఖ్యలు కనుక్కోవడానికి ఒకట్ల స్థానాన్ని 2 తో నింపుదాం.
మిగిలిన 4 స్థానాలను మిగిలిన 4 అంకెలతో (1,1,2,3) నింపే విధానాలు \(\frac{4 !}{2 !}=12\)
కనుక దత్త అంకెలతో ఏర్పరచగల 5 అంకెల సరి సంఖ్యల సంఖ్య =12

ప్రశ్న 23.
మూడు వేర్వేరు పుస్తకాలకు ఒక్రోదానికి నాలుగు ప్రతులున్నాయి. ఈ 12 పస్తకాలను ఒక అరలో ఎన్ని రకాలుగా అమర్చవచ్చు ?
సాధన:
దత్తాంశం (ప్రకారం, ఇచ్చిన 12 పుస్తకాలలో 4 పుస్తకాలు ఒక రకంగా, 4 పుస్తకాలు రెండో రకంగా, 4 పుస్తకాలు మూడో రకంగా ఉన్నాయి. కనుక సిద్ధాంతం 5.5 .2 (ప్రకారం ఈ 12 పుస్తకాలను ఒక అరలో అమర్చే విధానాలు.
\(\frac{12 !}{4 ! 4 ! 4 !}\)

ప్రశ్న 24.
EAMCET పదంలోని అక్షరాలతో ఏర్పడే 6 అక్షరాల పదాలన్నింటినీ నిఘంటువులోని క్రమంలో అమరిస్తే, ఆ క్రమంలో EAMCET పదం యొక్క కోటిని కనుక్కోండి.
సాధన:
దత్తపదం EAMCET లోని అక్షరాల నిఘంటువు క్రడుం ACEEMT నిఘంటువులో ముందుగా A తో మొదలజ్యే పదాలన్నీ వస్తాయి. కనుక మొదటిి స్థానాన్ని A తో నింపితే మిగిలిన 5 అక్షరాలను \(\frac{5 !}{2 !}\) విధాలుగా (2E’ లు ఉన్నవి కనుక) అమర్చవచ్చు. ఈ విధంగా చేసుకొంటూ EAMCET పదం వచ్చే వరకూ కింది విధంగా గణిస్తాం.

ప్రశ్న 25.
ఎనిమిదిమంది పురుషును, నలుగురు స్త్రీలను ఒక వృత్తాకార బల్ల చుట్టూ ఎన్ని రకాలుగా అమర్చవచ్చు ? వీటిలో ఎన్ని (ప్తస్తారాలలో
(i) స్త్రీలంతా ఒకేచోట ఉంటారు.
(ii) ఏ ఇద్దరు స్త్రీలు పక్క పక్కన రాకుండా ఉంటారు.
సాధన:
మొత్తం వ్యక్తుల సంఖ్య = 12 (ఎనిమిదిమంది పురుషులు + నలుగురు స్త్రీలు
కనుక వీరిని వృత్లాకార బల్ల చుట్టూ అమర్చే విధానాలా = (11)!

(i) నలుగురు స్త్రీలను ఒక యూనిట్గా భావిస్తే, ఎనిమిది మంది పురుషులు ఎనిమిది యూనిట్లు అనుకుంటే ఈ తామ్మిది యూనిట్లను వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు= 8!
ఇప్పుడు నలుగురు స్త్రీలను వారిలో వారిని 4! విధాలుగా అమర్చవచ్చు.
∴ స్త్రీలంతా ఒకచోట ఉండేలా అమర్చగల విధానాల సoఖ్య = 8! × 4!

(ii) ముందుగా ఎనిమిది మంది పురుషులను ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు =(8-1)! = 7! వీరిలో ప్రతి ఇద్దరు పురుషుల మధ్య

ఒక్కో ఖాళీ చొప్పున మొత్తం 8 ఖాళీలు ఉంటాయి. (ఈ ఖాళీలను పైన పటంలో x అనే గుర్తుతో సూచించాం) ఇప్పుడు ఈ 8 ఖాళీలలో నలుగురు స్త్రీలను అమర్చే విధానాలు= ⁸P₄ కనుక ఏ ఇద్దరు స్త్రీలు పక్క పక్కన లేని వృత్తాకార ప్రస్తారాల సoఖ్య 7! × ⁸P₄.

ప్రశ్న 26.
అయిదురుగురు భారతీయులను, నలుగురు అమెరికా దేశస్థులను, ముగ్గురు రష్యా దేశస్థులను ఒక వృత్తాకార ఐల్ల చుట్టా
(i) భారతీయులంతా ఒకే చోట కలిసి ఉండేలా
(ii) ఏ ఇద్దరు రష్యా దేశస్థులు పక్క పక్కన లేకుండా
(iii) ఒక దేతానికి చెందిన వారందరూ ఒకేచోట ఉండేలా ఎన్నిరకాలుగా అమర్చవచ్చు) ?
సాధన:
(i) అయిదుగురు భారీీయలను ఒక యూనిట్గా భావిస్తే, నలుగురు అమెరికా దేశస్థులు, ముగ్గరు రష్యా దేశస్థులు. 1 యూనిట్ భారతీయులు అంటే 8 మంది వ్యక్తులుంటారు. వీరిని ఒక వృత్తారార బల్లచుట్టూ అమర్చే విధానాలు
= (8-1)! = 7 !
ఇప్పుడు అయిదుగురు భారతీయులను వారిలో వారిని 5! విధాలుగా అమర్చవచ్చు. కనుక కావలసిన వృత్తాకార [ప్రస్తారాల సంఖ్య =7! × 5 !

(ii) ముందుగా ముగ్గరు రష్యా దేశస్థులను ఒక పక్కుగా ఉంచి, మిగిలిన 9 మంది వ్యక్తులను (అయిదుగురు భారతీయులు + నలుగురు అమెరికా దేశస్థులు) ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు =(9-1)!=8 ! ఇప్పుడు, ఈ 9 మంది వ్యక్తుల మధ్యలో ఖాళీలు 9 ఉంటాయి.
ఈ 9 ఖాళీలలో ముగ్నురు రష్లా దేశస్థులను అమర్చే విధానాలు ⁹P₃
కనుక కావలసిన వృత్తాకార (ప్రస్తారాల సంఖ్య 8! × ⁹P₃

(iii) అయిదుగురు భారతీయులను ఒక యూనిట్, నలుగురు అమెరికా దేశస్థులను రెండ్ర యూనిట్గానూ ముగ్గురు రష్యా దేశస్థులను మూడో యూనిట్గాను భావిస్తే 3 యూనిట్లు అవుతాయి. ఈ మూడు యూనిట్లతో వచ్చే వృత్తాకార ప్రస్తారాల సంఖ్ =(3-1) !=2 !
ఇప్పుడు అయిదుగురు భారతీయులను వారిలో వారిని అమర్చే విధానాలు 5!. ఇదే విధంగా నలుగురు అమెరికా దేశస్కులను 4! విధాలుగానూ, ముగ్గురు రష్యా దేశస్థులను 3! విధాలుగానూ అమర్చవచ్చు, కనుక కావలసిన విధానాలు
=2! × 5! × 4! × 3!

ప్రశ్న 27.
విభిన్నమైన రంగుల హూసలతో ఏర్పరచగల పూసల గొలుసుల సంఖ్యను కనుక్రోండి.
సాధన:
n అసరూప వస్తువులతో ఏర్పరచగల వేలాడే రకం వృత్తాకార ప్రస్తారాల సంఖ్య \(\frac{1}{2}(n-1)\) ! అని మనకు తెలుసు.
కనుక ఇచ్చిన 7 పూసలతో ఏర్పరచగల దండల సంఖ్య
\(\frac{1}{2}(n-7) !=\frac{1}{2}(6 !)=360\)

ప్రశ్న 28.
7 విభిన్నమైన ఎర్ర గులాబీలు, 4 విభిన్నమైన పసుపు రంగు గులాబీలతో 3 రెండు పసుపు రంగు గులాబీలు పక్క పక్కన రాకుండా ఎన్ని రకాలుగా దండలు తయారు చేయవచ్చు?
సాధన:
ముందుగా 7 విభిన్నమైన ఎర్రగులాబీలతో ఏర్పరచగల వృత్తాకార (ప్తస్తారాల సంఖ్య =(7-1)!=6!
ఈ 7 ఎర్రగులాబీల మధ్యలో ఉన్న 7 ఖాళీలలో 4 పసుఫు రంగుగులాబీలను ⁷P₄ విధాలుగా అమర్చవచ్చు. కనుక మొత్తం వృత్తాకార (ప్రస్తారాల సంఖ్య = 6 ! × ⁷P₄
కాని పువ్వుల దండలు వేలాడే వృత్తాకార ప్రస్తారాల కోవలోకి వస్తాయి. కనుక కావలసిన (ప్రస్తారాల సంఖ్య
\(=\frac{1}{2}\left(6 ! \times{ }^7 P_4\right)\)

ప్రశ్న 29.
ఒక వృత్తాకార బల్ల చుట్టూ 14మంది వ్యక్తులు కూర్చొని ఉన్నారు. వారిలో ఇద్దరు వ్యక్తలను (ప్కక్క పక్కన లేకుండా ఎన్ని రకాలుగా ఎంచుకోవచ్చు ?
సాధన. మనకు ఇచ్చిన 14 మంది వ్యక్తులు వృత్తాకార బల్ల చుట్టూ a₁  a₂ …………………… a₁₄ క్రమంలో పటంలోలాగా కూర్చొని ఉన్నారనుకొందాం.
ఈ 14 మంది వ్యక్తుల నుంచి ఇద్దరిని ఎంచుకొనే విధానాలు = ¹⁴C₂ =91.

ఈ విధానాలలో ఎంచుకొన్న ఇద్దరు వ్యక్తులు పక్క పక్కనే ఉండే విధానాలు a_1, a₂, a₂, a₃, ……………….. a_13,a₁₄, a₁₄, a₁₅ అంటే 14 విధానాలు కనుక ఎంచుకొన్న ఇద్దరు వ్యక్తులు పక్కపక్కన లేని విధానాలు =91-14 = 77

ప్రశ్న 30.
ఎనిమిది మంది బాలురు, అయిదుగురు బాలికల నుంచి నలుగురు బాలురు, ముగ్నురు బాలికలు ఉండేలా ఎన్ని కమిటీలా ఎంచుకోవచ్చు ?
సాధన:
ఇచ్చిన ఎనిమిది మంది బాలుర నుంచి నలుగురు బాలురను ఎంచుకొనే విధానాల సంఖ్య = ⁸C₄
ఇంకా అయిదుగురు బాలికల నుంచి ముగ్గురు బాలికలను ఎంచుకొనే విధానాలు = ⁵C₃
కనుక, ప్రాఠామిక సూత్రం ప్రకారం నలుగురు బాలురు, ముగ్గురు బాలికలను ఎంచుకొనే విధానాలు.
= ⁸C₄ × ⁵C₃ = 70 × 10 = 700

ప్రశ్న 31.
విభిన్నమైన 7 ఇంగ్లీష, 6 తెలుగు, 5 హిందీ పుస్తకాల నుంచి 4 ఇంగ్లీష, 3 తెలుగు, 2 హిందీ పుస్తకాలను ఎంచుకొనే విధానాలు ఎన్ని?
సాధన:
ముందుగా 7 ఇంగ్లీషు పుస్తకాల నుంచి 4 పుస్తకాలను ఎంచుకొనే విధానాలు = ⁷C₄
6 తెలుగు పుస్తకాల నుంచి 3 తెలుగు పుస్తకాలను ఎంచుకొనే విధానాలు = ⁶C₃
5 హిందీ పుస్తకాల నుంచి 2 హిందీ పుస్తకాలను ఎంచుకొనే విధానాలు = ⁵C₂
కనుక, కావలసిన విధానాలు
= ⁷C₄ x ⁶C₃ x ⁵C₂

ప్రశ్న 32.
ఆరుగురు బాలురు, నలుగురు బాలికలనుంచి కనీసం ఒక బాలిక ఉండేలా నలుగురు సభ్యలున్న కమిటీలు ఎన్ని ఏర్పరచవచ్బు ?
సాధన:
ఏ నిబంధనా లేకుండా మొత్తం 10 మంది వ్యక్తుల (ఆరుగురు బాలురు + నలుగురు బాలికలు) నుంచి నలుగురు సభ్యులున్న కమిటీని ఎంచుకొనే విధాలు ¹⁰C₄ వీటిలో అసలు బాలికలు లేకుండా బాలురు మాత్రమే ఉండేటట్లు కమిటీ ఎంచుకొనే విధాలు ⁶C₄ కనుక కనీసం ఒక బాలికైనా ఉండే కమిటీల సంఖ్య
= ¹⁰C₄  – ⁶C₄= 210 – 15 = 195.

ప్రశ్న 33.
ఏడుగురు బాట్స్మెన్, అరుగురు బౌలర్లు, ఇద్దరు వికెట్ కీపర్లు నుంచి కనీసం నలుగురు బౌలర్లు, ఒక వికెట్ కీపరు ఉండేలా 11 మంది ఆటగాళ్ళతో క్రికట్ టీమును ఎన్ని రకాలుగా ఎంచుకోవచ్చు ?
సాధన:
కనీసం నలుగురు బౌలర్లు, ఉండాలంటే టీమును కింద చూపిన విధాలుగా ఎంచుకోవచ్చు.

కనుక కోరిన విధంగా క్రికెట్ టిముని ఎంచుకొనె విధానాలు =315+210+35=560.

ప్రశ్న 34.
‘m’ సమాంతర రేఖలా మరాక ‘n’ సమాంతరరేఖలను (మొదటి రేఖలకు సమాంతరంగా లేని) ఖండిస్తే ఎన్ని సమాంతర చతుర్భుజాలేర్పడతాయి ?
సాధన:
ఒక సమాంతర చతుర్భుజం ఏర్పడాలంటే మొదటి m సరళరీఖల నుంచి 2 సరళరేఖలు ఎంచుకోవాలి. ఈ విధానాలు ^mC₂ రెండో సమితిలోని n సరళ రేఖల నుంచి 2 సరళరేఖలు ఎంచుకోవాలి. ఈ విధానాల సంఖ్య ⁿC₂ కనుక, దత్త సరళరేఖలు ఖండించుకోవడం వల్ల ఏర్పడే సమాంతర చతుర్భుజాల సంఖ్య = ^mC₂ x ⁿC₂

ప్రశ్న 35.
ఒక తలంలో m బిందువులున్నాయి. వాటిలో p బిందువులు సరేఖీయాలు,మిగిలిన బిందువులలో 3 మూడు బిందువులు సరేఖీయాలు కాకపోతే, ఈ బిందువులను రేఖాఖండాల ద్వారా కలిపితే వచ్చే విఖిన్న
(i) రేఖా ఖండాలెన్ని?
(ii) త్రిభజాలెన్ని ?
సాధన.
(i) ఇచ్చిన m బిందువుల నుంచి రెండు బిందువులను ఎంచుకొని కలిపితే ఒక రేఖాఖండం వస్తుంది. కనుక ^mC₂ రేఖాఖండాలు రావాలి. కాని m బిందువులలో p బిందువులు సరేఖీలయాలు కనుక ఈ బిందువులను వాటిలో వాటిని రెండు బిందువుల చాప్పున కలిపితే ^pC₂ రేఖాఖండాలు రావడానికి బదులుగా 1 రేఖాఖండం మాత్రమే వస్తుంది. కనుక దత్త m బిందువులను కలపడం ద్వారా వచ్చే విభిన్న రేఖాఖండాల సంఖ్య = ^mC₂ – ^pC₂ +1

(ii) ఇచ్చిన m బిందువులను 3 బిందువుల చొప్పున కలిపితే తిిభుజాలు ఏర్పడతాయి. కనుక ^mC₃ తిిభుజాలు రావాలి.కాని ఈ m బిందువులలో P బిందువులు సరేఖీయాలు కనుక ఈ p బిందువుల నుంచి 3 బిందువుల చాప్పున ఎంచుకొని కలిపితే ^pC₃ (తిభుజాలు దావడానికి బదులుగా ఒక రేఖాఖండం వస్తుంది. (అంటే ఒక్క (యిభుజం కూడా రాదు.) కనుక ఇచ్చిన m బిందువులను కలపడం ద్వారా ఏర్పడే తి่భుజాల సంఖ్య = ^mC₃ – ^pC₃ 

ప్రశ్న 36.
ఒక ఉపాధ్యాయుడు పదిమంది విద్యార్థులను పార్కుకు తీసుకువెళ్ళాలి. ఒక్కొక్కసారి ముగ్నురు విద్యార్థుల చొప్పున తీసుకు వెళ్ళగలరు. కాని ఏ ముగ్గురు విద్యార్థుల బృందాన్నైనా ఒక్కసారి మాత్రమే తీసుకాని వెళ్ళాలి ?
(i) ప్రతీ విద్యార్థికి ఎన్ని సార్లు పార్కుకు వెళ్ళే అవకాశం ఉoది?
(ii) ఉపాధ్యాయుడు ఎన్నిసార్లు పార్కుకు వెళ్ళే అవకాశం ఉoది ?
సాధన:
(i) పదిమంది విద్యార్థులలో x ఒకరు అనుకొందాం. పార్కుకు x వెళ్ళే (పతిసారి ఇంకా ఇరువురు విద్యార్థులను మిగిలిన తొమ్మిది మంది విద్యార్థుల నుంచి ఎంచుకోవాలి. ఈ పనిని ⁹C₂ విధాలుగా చేయవచ్చు.అంటే
x పార్కుకు ⁹C₂ = 36 సార్లు వెళతాడు.

(ii) పదిమంది విద్యార్థుల నుంచి ముగ్గురు విద్యార్థును ఎంపిక చేసిన ప్రతిసారి ఉపాధ్లాయుడు పార్కుకు వెళ్తాడు. కనుక ఉపాధ్యాయుడు ¹⁰C₃ =120 సార్లు పార్కుకు వెళతాడు.

ప్రశ్న 37.
ఒక రెండంతస్తుల బస్సుకు కింది అంతస్తులో 8 సీట్లు, పై అంతస్తులో 10 సీట్లు ఉన్నాయి. ఈ బస్సులో (ప్రయాణించవలసిన 18 ప్రయాకులల్లో ముగ్గురు పిల్లలు పై అంతస్తులో మాత్రమే వెళ్ళాలి. ఇంకా నలుగురు వృద్దులు పైఅంతస్తుకు వెళ్ళలేరు అని ఇస్తే వారిని ఎన్ని విధాలుగా అమర్చవచ్చు ?
సాధన:
ముగ్గురు పల్లలు పై అంతస్థులోనూ, నలుగురు వృద్ధులు కింది అంతస్తులోనూ ప్రయాణిస్తారనుకాంటే మిగిలిన ప్రయాణీకులు 11 మంది ప్రయాణీకులలో 7 కింది అంతస్తులో, 7 మంది పై అంతస్తులో ప్రయాణించాలి. కనుక 11 మంది 7 ఎంచుకొనే విదానాలు
¹¹C₇ కింది అంతస్తులోని 8 సీట్లలో 8! విధాలు గానూ, పై అంతస్థులోని 10 సీట్లలో (10)! విధాలుగానూ అమర్చవచ్చు. కనుక
మొత్తం విధానాల సంఖ్య = ¹¹C₇ × 10! × 8!

ప్రశ్న 38.
(i) \({ }^{10} C_3+{ }^{10} C_6={ }^{11} C_4\)
(ii) \({ }^{25} C_4+\sum_{r=0}^4{ }^{(29-r)} C_3={ }^{30} C_4\) అని నిరూపించండి.
సాధన:

ప్రశ్న 39.
(i) \({ }^{12} \mathrm{C}_{s+1}={ }^{12} \mathrm{C}_{2 \mathrm{~s}-5^{\prime}}\) అయితే s కనుక్కోండి.
(ii)\({ }^n C_{21}={ }^n C_{27} \text {, అయితే }{ }^{50} C_n\) విలువ కనుక్కోండి
సాధన:

ప్రశ్న 40.
ఒకే రకమైన 5 కలాలు, ఒకేరకమైన 6 పెన్సిళ్ళు, ఒకే రకమైన 7 రబ్బర్లు ఉన్నాయి. వాటి నుంచి ఎన్ని వస్తువులనైనా (కనీసం ఒకటి) ఎంచుకొనే విధానాలు సంఖ్యను కనుక్కోండి.
సాధన:
ఎంచుకొనే విధానాల సంఖ్య
= (5+1) (6+1) (7+1) -1 = 335

ప్రశ్న 41.
1080 సంఖ్యకు (1 సంఖ్యతో సహా) ధన భాజకాల సంఖ్యను కనుక్కోండి.
సాధన.
1080=2³ × 3³ × 5¹ (ప్రధాన అంకెల లబ్దం)
= (3+1) (3+1) (1+1)
= 4 × 4 × 2 = 32

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 4 సమీకరణ వాదం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 4 సమీకరణ వాదం

ప్రశ్న 1.
2,3,6 లు మూలాలుగా గల 3 వ తరగతి ఏక బహంపది సమీకరణాన్ని రూపొందించండి.
సాధన:
కావలసిన బహుపది సమీకరణ
(x-2)(x-3)(x-6) = 0
⇒ x³-11 x²+36 x-36=0

ప్రశ్న 2.
3x³-10x²+7 x+10=0 ఘన సమీకరణం యొక్క మాలాలు, గుణకాల మధ్య సంబంధాలను కనుక్కోండి.
సాధన:
3x³-10x²+7x + 10 = 0 ……………. (1)
(1) ను ax³+bx²+c x+d=0 తో పోల్చగా

ప్రశ్న 3.
x⁴-2x³+4x²+6 x-21=0 ద్వివర్గ సమీకరణం యొక్క మాలాలు, గుణకాల మధ్య సంణంధాలను కనుక్కోండి.
సాధన:
దత్త సమీకరణం
x⁴-2x³+4x²+6 x-21=0
ax⁴+b x³+cx²+dx+e=0  తో పోల్చగా
a=1, b=-2, c=4, d=6, e=-21

ప్రశ్న 4.
x⁴+a x³+b x²+c x+d=0 సమీకరణం మొక్క మూలాలు 1, 2, 3, 4 బయితే a, b, c, d విలువలు కనుక్కోండి.
సాధన:
దత్త సమీకరణ మూలాలు 1, 2, 3, 4
కనుక  x⁴+a x³+b x²+c x+d
≡ (x-1) (x-2) (x-3) (x-4)=0
≡ x⁴-10x³+35x²– 50x+24=0
ఇరువైపుల పదాల గుణకాలను పోల్చగా
a=-10, b=35, c=-50, d=24

ప్రశ్న 5.
సమీకరణం x³-p x²+q x-r=0 మూలాలు a,b,c ల అయి, r ≠ 0 అయితే, అప్పుడు \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\) ను p, q, r లలో కనుక్కోండి.
సాధన:
a, b, c లు
x³-p x²+q x-r=0 కు మూలాలు
a+b+c=p, a b+b c+c a=q, a b c=r

ప్రశ్న 6.
x³-p x²+q x-r=0 సమీకరణ యొక్క మాలాల వర్గాల మొత్తాన్ని, ఘనాల మెత్తాన్ని p q r  లలో కనుక్కోండి.
సాధన:

ప్రశ్న 7.
x³+p₁ x²+p₂ x+p₃=0 సమీకరణం యొక్క మూలాల వర్గాలు మూలాలాగా ఉండే ఘన సమీకరణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 8.
x³+px²+qx+r =0 మాలాలు α, β, γ లు అయితే కింది వాటిని కనుక్కోండి.
(i) ∑ a²
(ii) ∑ \(\frac{1}{\alpha}\)
(iii) ∑ a³
(iv) ∑ β² γ²
(v) (α + β) (β + γ ) (γ + α )

(i) ∑ a²
సాధన:
α² + β² +  γ²
=(α+β+γ)² -2(αβ + βγ+ γ α)
p² – 2q

(ii) ∑ \(\frac{1}{\alpha}\)
సాధన:
\(\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}=\frac{\beta \gamma+\gamma \alpha+\alpha \beta}{\alpha \beta \gamma}=\frac{-q}{r}\)

(iii) ∑ α³
సాధన:
∑ α³ 
= (α+ β + γ) (a² + β² + γ² – αβ + βγ +γα)+3αβγ
= (- p)(p² -2q – q) – 3r
= – p(p²– 3q) – 3r
∴ ∑ α³ = – p³ + 3pq – 3r = 3pq – p³– 3r

(iv) ∑ β² γ²
సాధన:

(v) (α + β) (β + γ ) (γ + α )
సాధన:
α + β + γ = – p
⇒ α + β = – p – γ మరియు β + γ = – p – α
= γ + α = – p – β
∴ (α + β) (β + γ) (γ + α)
= ( – p – γ)( – p – α) ( – p – β)
=-p³-p² (α + β + γ) – p (αβ+βγ+γα)-αβγ
= -p³ + p³-pq + r = r – pq

ప్రశ్న 9.
x³+ax²+b x+c=0 మూలాలు α,β,γ లు అయితే ను కనుక్కోండి.
సాధన:
α,β,γ లు దత్త సమీకరణం యొక్క మూలాలు కనుక
α + β + γ = – α, αβ + βγ + γα = b, αβγ = c

ప్రశ్న 10.
α,β,γ లు x³+p²+q x+r=0 మూలాలు అయితన,  లు మూలాలుగా గల ఏక ఘన సమీకరణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 11.
x³-3x²-16 x+48=0 ను సాధించండి.
సాధన:
f(x)=x³-3 x²-16 x+48 అనుకోండి
యత్న – దోష పద్ధతిన f(3)=0
కనుక f(x)=0 కు 3 మూలం
f(x) ను (x-3) చే భాగించగా

ప్రశ్న 12.
x⁴-16 x³+86x²-176 x+105=0 యึక్క మాలాలను కనుక్కోండి.
సాధన:

∴ g(x) & =(x-3)(x²-12 x+35)
=(x-3)(x-5)(x-7)
∴ f(x) & =(x-1)(x-3)(x-5)(x-7)
∴ దత్త సమీకరణం మూలాలు 1,3,5,7

ప్రశ్న 13.
x³-7x²+36=0 సమీకరణం మొక్క ఒక మాలం మరో దానికి రెట్టింప అయితే, సమీంరాాన్ని సాధించండి.
సాధన:
x³-7x²+36=0 కు మూలాలు α, β, γ లు అనుకోండి.
β =2α అనుకుందాం
అయిన α + β + γ = 7
⇒ 3α + γ  =7 ………….. (1)

ప్రశ్న 14.
x³-6x²+3 x+10=0 సమీకరాానికి ఒక మూలం 2 అయితే, మిగిలిన మాలాలను కనుక్కోండి.
సాధన:
f(x)=x³-6x²+3 x+10 అనుకానుము.
f(x)=0 కు 2 మూలం కనుక f(x) ను (x-2) చే భాగించగా

x³-6x²+3 x+10 = (x – 2)(x² – 4x – 5)
(x-2) (x+ 1) (x-5)

ప్రశ్న 15.
4x³+20x²-23 x+6=0 సమీకరణం యొక్క రెండు మూలాలు సమానమైతే, సమీకరణం యొక్క మాలాలన్నింటిని కనుక్కోండి.
సాధన:
α,β,γ లు  4x³+20x²-23 x+6=0  కు మూలాలు. రెండు మూలాలు సమానం కనుక α = β అనుకోండి.

పరిశీలనవల్ల
α = \(\frac{1}{2}\) దత్త సమీకరణానికి మూలం
(2) ⇒ γ = – 6
∴ దత్త సమీకరణం మూలాలు \(\frac{1}{2}, \frac{1}{2},-6\)

ప్రశ్న 16.
x⁴– 2x³+4x³+6 x-21=0 సమీకరణం మొక్కరెండు మూలాల మొత్తం సున్న అయితే, సమీకరణ మొక్క మూలాలను కనుక్కోండి.
సాధన:
α, β, γ, δ లు దత్త సమీకరణ మూలాలు,
రెండు మూలాల మొత్తం సున్నీ కనుక
α + β = 0 అనుకొనుము.

ప్రశ్న 17.
4x³-24x²+23x+18=0 సమీకరణం యొక్క మూలాలు అంకశేఢిలో ఉంటీ, సమీంరణాన్ని సాధించండి.
సాధన:
a – d, a, a + d లు దత్త సమీకరణ మూలాలు అనుకోండి మూలాల మొత్తం
a – d + a + a + d = \(\frac{24}{4}\)
3a = 6
a = 2

ప్రశ్న 18.
x³-7x²+14x-8=0, సమీకరణం మూలాలు గుణరీశేధిలో ఉంటే, సమీకరణాన్ని సాధించండి.
సాధన:
దత్త సమీకరణం మూలాలు \(\frac{a}{r}\), a, అనుకుందాం. అప్పుడు

ప్రశ్న 19.
x⁴-5x³+5x³+5 x-6=0 సమీకరణం మొక్క రెండు మూలాల లబ్దం 3 అయితే ఆ సమీకరణాన్ని సాధించండి.
సాధన:
α, β, γ, δ లు మూలాలు అనుకుంటే.
వాటి లబ్దం αβγδ =-6
αβ=3 ( రెండు మూలాల లబ్దం 3)
∴ αβγδ = -6
γδ = – 2
α +β = p, γ, δ + q అనుకోండి
αβ లు మూలాలుగా గల సమీకరణం
x²-(α +β) x + αβ =0
x²-p x+3=0
γ ,δ లు మూలాలుగా గల సమీకరణం
x² – (γ + δ)x + γδ = 0
x² – qx – 2 = 0
x⁴ – 5x³ + 5x² + 5x – 6
= (x²-px-t- 3)(x²– qx – 2)
= x⁴ – (p + q) x³ + (1 + pq) x² +(2p-3q)x-6
సరిపదాల గుణకాలను పోల్చగా
p+q=5, 2p-3 q=5
∴ 2 p-3 q=5
3 p+3 q=15
5 p=20 ⇒ p=4
∴ q = 1
x² -4x+3=0 ⇒ (x-3)(x-1)=0
⇒ x=1,3
x²-x-2=0 ⇒ (x-2)(x+1)=0
⇒ x = -1,2
∴ దత్త సమీకరణం మూలాలు -1,2,1,3

ప్రశ్న 20.
x⁴+4x³-2x²-12x+9=0 సమీకరణానికి రంండు జతల సమాన మూలాలు ఉంటే, సమీకరణాన్ని సాధించండి.
సాధన:

x² + 2x+p = 0 = x²+2x – 3 = 0
⇒ (x-1-3) (x – 1) = 0
⇒ x = – 3,1
దత్త సమీకరణం మూలాలు -3, – 3, 1 ,1

ప్రశ్న 21.
p³ – 4 p q+8 r=0 అయితేనే x⁴+px³+q x² + rx+s=0 మొక్క రెండు మాలాల మొత్తం మిగిలిన రెండు మూలాల మొత్తానికి సమానమని నిరూపించండి.
సాధన:
దత్త సమీకరణం రెండు మూలాల మొత్తం మిగిలిన రెండు మూలాల మొత్తానికి సకానమని అనుకుందాం. α β γ δ అయ్యేటట్లు సమీకరణం మూలాలను α + β = γ + δ అనుకుందాం.

ప్రశ్న 22.
\(4+\sqrt{3}, 4-\sqrt{3}, 2+i, 2-i\) లను మాలాలుగా గల 4వ తరగతి ఏక ఱహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
\(4+\sqrt{3}, 4-\sqrt{3}\) లు మూలాలుగా గల సమీకరణం
2+i, 2 – i లు మూలాలుగా గల సమీకరణం
x²-4 x+5=0
కావలసిన సమీకరణం
(x²-8 x+13)(x²-4 x+5)=0
∴ x⁴-12x³+50x²-92 x+65=0

ప్రశ్న 23.
6x⁴-13 x³-35 x²-x+3=0 సమీకరణం యొక్క ఒక మూలం. \(2+\sqrt{3}\) అయితే సమీకరణాన్ని సాధించండి.
సాధన:

ప్రశ్న 24.
x⁴-6 x³+7x²-2 x+1=0 సమీకరణం మొక్క మూలాల వ్యతిరేక గుర్తులతో మాలాలు గల నాలుగో తరగతి ణహబపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
f(x) ≡  x⁴-6x³+7x²-2 x+1=0
కావలసిన సమీకరణం f(-x)=0
i.e., (-x)⁴-6(-x)³+7(-x)²-2(-x)+1=0
∴ x⁴+6x³+7x²+2x+1=0

ప్రశ్న 25.
6x⁴-7x³+8x²-7x+2=0 సమీకరణం మొక్క మాలాలకు 3 రెట్లున్న మాలాలు గల నాలుగో తరగతి బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
f(x) ≡ 6x⁴-7x³+8x²-7 x+2=0

ప్రశ్న 26.
\(x^3+\frac{x^2}{4}-\frac{x}{16}+\frac{1}{72}\) = 0 సమీకరణ మూలాలకు m రెట్లున్న మూలాలు గల మూడో తరగతి సమీకరణాన్ని రూపొందించి, m = 12 సందర్భానికి సమీకరణాన్ని రాణట్టండి.
సాధన:

ప్రశ్న 27.
x⁵+4 x³-x²+11=0 సమీకరణ మూలాలు -3 తో మార్పు చెందగా వచ్చే విలువలను మూలాలుగా కలిగిన 5వ తరగతి ణహంపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
f ≡ x⁵+4 x³-x²+11=0
కావలసిన సమీకరణం f(x+3)=0

ప్రశ్న 28.
4x⁴+32x³+83x²+76 x+21=0 మూలాలు 2 తో మార్పు చెందగా వచ్చే విలువలను మాలాలుగా గల 4 వ తరగతి బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
f(x) ≡ 4x⁴+32x³+83x²+76 x+21=0
కావలసిన సమీకరణం f(x-2)=0

ప్రశ్న 29.
x⁴+3x³-6 x²+2 x-4=0 సమీకరణ మాలాల వ్వత్కమ్మాలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 30.
x³-x³+8 x-6=0 మాలాల వర్గాలు మాలాలుగా గల ఐహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 31.
2x³+5x²+5 x+2=0 ఒకటో కోవకు చెందిన వ్కత్రమ సమీకరణమని చూపండి.
సాధన:
దత్త సమీకరణం 2x³+5x²+5 x+2=0
P₀ =2, P₁ =5, P₂ =5, P₃ =2
ఇచ్చట P₀ = P₃, P₁ = P₂
∴ 2x³+5x²+5 x+2=0 సమీకరణం ఒకటో కోవకు చెందిన వ్యుత్రమ సమీకరణం.

ప్రశ్న 32.
సాధించండి : 4x³-13x²-13 x+4=0
సాధన:
4x³-13x²-13x+4=0
ఒకటో కోవకు చెందిన బేసి పరిమాణ వ్యుత్కమమ సమీకరణం కనుక -1 దీనికి ఒక మూలం

4x²-17 x+4=0 4x²-16 x-x+4=0
4x(x-4)-1(x-4)=0
(x-4)(4 x-1)=0
x=4 (లేదా) \(\frac{1}{4}\)
∴ దత్త సమీకరణం మూలాలు -1,4, \(\frac{1}{4}\)

ప్రశ్న 33.
సాధించండి :
6x⁴-35x³+62x²-35 x+6=0
సాధన:
6x⁴-35x³+62x²-35 x+6=0

ప్రశ్న 34.
సాధించండ: :
x⁵-5x⁴+9x³-9x²+5 x-1=0
సాధన:
దత్త సమీకరణం
x⁵-5x⁴+9x³-9x²+5 x-1=0 రండో కోవకు చెందిన బేసి పరిమాణ వ్రుత్రమ సమీకరణం

ప్రశ్న 35.
సాధించండి :
6x⁶-25x⁵+31x⁴-31x²+25 x-6=0
సాధన:
దత్త సమీకరణం
6x⁶-25x⁵+3 x⁴-31x²+25 x-6=0 ఇది రెండవ కోవకు చెందిన సరి పరిమాణ వ్యుత్కమ సమీకరణం
∴ x² -1 అనేది

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 6 సమాకలనం Exercise 6(e) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 6 సమాకలనం Exercise 6(e)

అభ్యాసం 6(ఇ)

I. కింది సమాకలనులను గణించండి.

ప్రశ్న 1.
∫\(\frac{x-1}{(x-2)(x-3)}\) dx
సాధన:

= ∫\(\left(1+\frac{2}{x-3}\right)\) dx – ∫\(\left(1+\frac{1}{x-2}\right)\) dx
= x + 2ln |x – 3| – x – ln |x – 2| + C
= 2log |x – 3| – log |x – 2| + C

ప్రశ్న 2.
∫\(\frac{x^2}{(x+1)(x+2)^2}\) dx
సాధన:
\(\frac{x^2}{(x+1)(x+2)^2}\) ≡ \(\frac{A}{x+1}\) + \(\frac{B}{x+2}\) + \(\frac{C}{(x+2)^2}\)
⇒ x² = A(x + 2)² + B(x + 1)(x + 2) + C (x + 1)
x = -2 లో (1)
(-2)² = A(0) + B(0) + C(-2 + 1) ⇒ C = -4
x = -1 లో (1)
(-1)² = A(-1 + 2)² + 8(0) + C(0)
⇒ A = 1
(1) లో x² గుణకాలను సమానం చేయండి.
1 = A + B
⇒ B = 1 – A = 1 – 1 = 0

ప్రశ్న 3.
∫\(\frac{x+3}{(x-1)\left(x^2+1\right)}\) (May 07)
సాధన:
\(\frac{x+3}{(x-1)\left(x^2+1\right)}\) = \(\frac{A}{x-1}\) + \(\frac{\mathrm{Bx}+\mathrm{C}}{\mathrm{x}^2+1}\) అనుకొనుము
⇒ (x + 3) = A(x² + 1) + (Bx + C) (x – 1) – (1)
(1 ) లో x = 0 ప్రతిక్షేపించగా
3 = A(1) + C(-1)
⇒ A – C = 3 ⇒ C = A – 3 = 2 – 3 = 1
(1) లో x² గుణకాలను సమానం చేయండి.
0 = A + B
⇒ B = -A = -2

ప్రశ్న 4.
∫\(\frac{d x}{\left(x^2+a^2\right)\left(x^2+b^2\right)}\)
సాధన:

ప్రశ్న 5.
∫\(\frac{d x}{e^x+e^{2 x}}\)
సాధన:

ప్రశ్న 6.
∫\(\frac{d x}{(x+1)(x+2)}\)
సాధన:

ప్రశ్న 7.
∫\(\frac{1}{e^x-1}\) dx
సాధన:

ప్రశ్న 8.
∫\(\frac{1}{(1-x)\left(4+x^2\right)}\) dx
సాధన:
∫\(\frac{1}{(1-x)\left(4+x^2\right)}\) = \(\frac{A}{1-x}\) + \(\frac{B x+C}{4+x^2}\) అనుకోండి
⇒ 1 = A(4 + x²) + (Bx + C)(1 – x) —- (1)
(1) లో x = 1 ప్రతిక్షేపించగా
1 = A(4 + 1) ⇒ A = \(\frac{1}{5}\)
(1) లో x = 0 ప్రతిక్షేపించగా
1 = A(4) + C(1)
⇒ C = 1 – 4A = 1 – 4\(\left(\frac{1}{5}\right)\) = \(\frac{5-4}{5}\) = \(\frac{1}{5}\)
(1) లో x² గుణకాలను సమానం చేయగా
0 = A – B
⇒ B = A = \(\frac{1}{5}\)

ప్రశ్న 9.
∫\(\frac{2 x+3}{x^3+x^2-2 x}\) dx
సాధన:

⇒ (1) లో x = 0 ప్రతిక్షేపించగా
3 = A(2)(-1) + B(0) + C(0)
⇒ A = –\(\frac{3}{2}\)
(1) లో x = 1 ప్రతిక్షేపించగా
2 + 3 = A(0) + B(0) + C(1)(3)
⇒ C = \(\frac{5}{3}\)
(1) లో x = -2 ప్రతిక్షేపించగా
2(-2) + 3 = A(0) + B(-2)(-2 – 1) + C(0)
⇒ -1 = 6B ⇒ B = \(\frac{-1}{6}\)

II. కింది సమాకలనులను గణించండి.

ప్రశ్న 1.
∫\(\frac{d x}{6 x^2-5 x+1}\)
సాధన:

ప్రశ్న 2.
∫\(\frac{d x}{x(x+1)(x+2)}\)
సాధన:
\(\frac{1}{x(x+1)(x+2)}\) ≡ \(\frac{A}{x}\) + \(\frac{\mathrm{B}}{\mathrm{x}+1}\) + \(\frac{c}{x+2}\)
⇒ 1 ≡ A(x + 1)(x + 2) + B(x)(x + 2) + C(x)(x + 1)
x = 0 ప్రతిక్షేపించగా
1 = A(1) (2) + B(0) + C(0) ⇒ A = \(\frac{1}{2}\)
x = -1 ప్రతిక్షేపించగా
1 = A(0) + B(-1)(-1 + 2) + C(0)
⇒ 1 = -B ⇒ B = -1
x = -2 ప్రతిక్షేపించగా

ప్రశ్న 3.
∫\(\frac{3 x-2}{(x-1)(x+2)(x-3)}\) dx
సాధన:
\(\frac{3 x-2}{(x-1)(x+2)(x-3)}\) ≡ \(\frac{A}{x-1}\) + \(\frac{B}{x+2}\) + \(\frac{c}{x-3}\)
⇒ 3x – 2 = A(x + 2) (x – 3) + B(x – 1)(x – 3) + C(x – 1)(x + 2)
x = 1 ప్రతిక్షేపించగా
3(1) – 2 = A(1 + 2)(1 – 3) + B(0) + C(0)
⇒ A = \(\frac{-1}{6}\)
x = 3 ప్రతిక్షేపించగా
3(3) – 2 = A(0) + B(0) + C (3 – 1) (3 + 2)
C = \(\frac{7}{10}\)
x = -2 ప్రతిక్షేపించగా
3(-2) – 2 = A(0) + B(-2-1)(-2-3) + C(0) – 8
= 15B ⇒ B = \(\frac{-8}{15}\)

ప్రశ్న 4.
∫\(\frac{7 x-4}{(x-1)^2(x+2)}\) dx
సాధన:
\(\frac{7 x-4}{(x-1)^2(x+2)}\) ≡ \(\frac{A}{x-1}\) + \(\frac{B}{(x-1)^2}\) + \(\frac{c}{x+2}\)
⇒ 7x – 4 = A(x – 1) (x + 2) + B(x + 2) + C(x – 1)² —- (1)
x = 1 లో ప్రతిక్షేపించగా
7 – 4 = A(0) + B(1 + 2) ⇒ B = 1
x = -2 లో (1) ప్రతిక్షేపించగా
7(-2) – 4 = A(0) + B(0) + C(-2-1)²
⇒ -18 = 9C ⇒ C = -2

III. కింది సమాకలనులను గణించండి.

ప్రశ్న 1.
∫\(\frac{1}{(x-a)(x-b)(x-c)}\) dx
సాధన:

x = b ప్రతిక్షేపించగా
1 = A(0) + B(b – a) (b – c) + C(0)

ప్రశ్న 2.
∫\(\frac{2 x+3}{(x+3)\left(x^2+4\right)}\) dx
సాధన:
\(\frac{2 x+3}{(x+3)\left(x^2+4\right)}\) = \(\frac{A}{x+3}\) + \(\frac{B x+C}{x^2+4}\) అనుకోండి
2x + 3 = A(x² + 4) + (Bx + C) (x + 3)
x = -3 ⇒ -3 = A(9 + 4) = 13 A
A = –\(\frac{3}{13}\)
x² గుణకాలు సమానం చేయగా
0 = A + B ⇒ B = -A = \(\frac{3}{13}\)
స్థిరపదాలు సమానం చేయగా
3 = 4A + 3C
3C = 3 – 4A = 3 + \(\frac{12}{13}\) = \(\frac{39+12}{13}\) = \(\frac{51}{13}\)

ప్రశ్న 3.
∫\(\frac{2 x^2+x+1}{(x+3)(x-2)^2}\) dx
సాధన:
\(\frac{2 x^2+x+1}{(x+3)(x-2)^2}\) = \(\frac{A}{x+3}\) + \(\frac{B}{x-2}\) + \(\frac{C}{(x-2)^2}\) అనుకోండి
2x² + x + 1 = A(x – 2)² + B(x + 3) (x – 2) + C(x + 3)
x = 2 ⇒ 8 + 2 + 1 = C(2 + 3) = 5C
⇒ C = \(\frac{11}{5}\)
x = -3 ⇒ 18 – 3 + 1
= A(-5)² = 25A ⇒ A = \(\frac{16}{25}\)
x² గుణకాలు సమానం చేయగా

ప్రశ్న 4.
∫\(\frac{d x}{x^3+1}\)
సాధన:

⇒ 1 = A(x² – x + 1) + (Bx + C)(x + 1) —– (1)
(1) లో x = -1 ప్రతిక్షేపించగా
1 = A(1 + 1 + 1) + (-B + C)(0)
⇒ 3A = 1 ⇒ A = \(\frac{1}{3}\)
(1) లో x = 0 ప్రతిక్షేపించగా
1 = A(1) + C(1)
⇒ C = 1 – A = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
x² గుణకాలు సమానం చేయగా
O = A + B ⇒ B = -A = –\(\frac{1}{3}\)

ప్రశ్న 5.
∫\(\frac{\sin x \cos x}{\cos ^2 x+3 \cos x+2}\) dx
సాధన:
cos x = t ⇒ – sin x dx = dt
∫\(\frac{\sin x \cdot \cos x d x}{\cos ^2 x+3 \cos x+2}\) = ∫\(\frac{-t d t}{t^2+3 t+2}\)

(2) లో t = -1 ప్రతిక్షేపించగా
-1 = A(-1 + 2) ⇒ A = -1
(2) లో t = -2 ప్రతిక్షేపించగా
-2 = B(-2 + 1) ⇒ B = 2