AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.1 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers Exercise 1.1
![]()
Question 1.
Name the properly Involved in the following examples.

vii) 7a + (-7) = 0
viii) x + \(\frac{1}{x}\) = 1(x ≠ 0)
ix) (2 x x) + (2 x 6) = 2 x (x + 6)
Solution:
i) Additive identity
ii) Distributive law
iii) Multiplicative identity
iv) Multiplicative identity
v) Commutative law of addition
vi) Closure law in multiplication
vii) Additive inverse
viii) Multiplicative inverse
ix) Distributive
![]()
Question 2.
Write the additive and the multiplicative inverses of the following.
i) \(\frac{-3}{5}\)
ii) 1
iii) 0
iv) \(\frac{7}{9}\)
v) -1
Solution:

Question 3.
Fill in the blanks
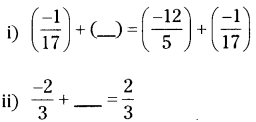

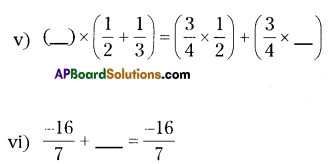
Solution:
i) \(\left(\frac{-12}{5}\right)\)
ii) \(\left(\frac{4}{3}\right)\)
iii) \(\left(\frac{9}{11}\right)\)
iv) \(\left(\frac{6}{7}\right)\)
v) \(\left(\frac{3}{4}, \frac{1}{3}\right)\)
vi) 0
![]()
Question 4.
Multiply \(\frac{2}{11}\) by the reciprocal of \(\frac{-5}{14}\)
Solution:
The reciprocal of \(\frac{-5}{14}\) is \(\frac{-14}{5}\)
( ∵ \(\left(\frac{-5}{14}\right) \times\left(\frac{-14}{5}\right)=1\) )
∴ The product of \(\frac{2}{11}\) and \(\frac{-14}{5}\) is
\(\frac{2}{11} \times\left(\frac{-14}{5}\right)=\frac{-28}{55}\)
Question 5.
Which properties can be used computing \(\frac{2}{5} \times\left(5 \times \frac{7}{6}\right)+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)\)
Solution:
The following properties are involved in the product of
\(\frac{2}{5} \times\left(5 \times \frac{7}{6}\right)+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)\)
i) Multiplicative associative property.
ii) Multiplicative inverse.
iii) Multiplicative identity.
iv) Closure with addition
Question 6.
Verify the following
\(\left(\frac{5}{4}+\frac{-1}{2}\right)+\frac{-3}{2}=\frac{5}{4}+\left(\frac{-1}{2}+\frac{-3}{2}\right)\)
Solution:

![]()
Question 7.
Evaluate \(\frac{3}{5}+\frac{7}{3}+\left(\frac{-2}{5}\right)+\left(\frac{-2}{3}\right)\) after rearrangement.
Solution:
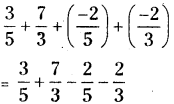
Let x = \(1.2 \overline{4}\)
⇒ x = 1.244……. …………………(1)
Here periodicity of equation (1) is 1. So
it should be multiplied by 10 on both
sides.
⇒ 10 x x = 10 x 1.244
10x = 12.44 …………..(2)

![]()
Question 8.
Subtract
(i) \(\frac{3}{4}\) from \(\frac{1}{3}\)
(ii) \(\frac{-32}{13}\) from 2
(iii) -7 from \(\frac{-4}{7}\)
Solution:
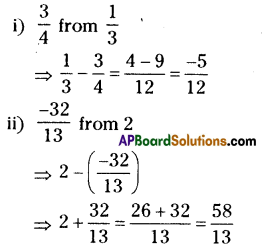
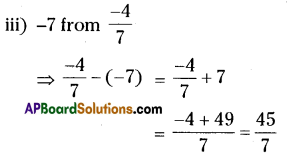
Question 9.
What numbers should be added to \(\frac{-5}{8}\) so as to get \(\frac{-3}{2}\) ?
Solution:
Let the number to be add ‘x’ say

∴ \(\frac{-7}{8}\) should be added to \(\frac{-5}{8}\) then we will get \(\frac{-3}{2}\)
Question 10.
The sum of two rational numbers is 8 If one of the numbers is \(\frac{-5}{6}\) find the other.
Let the second number be ‘x’ say
⇒ \(x+\left(\frac{-5}{6}\right)=8\)
⇒\(8+\frac{5}{6}=\frac{48+5}{6}=\frac{53}{6}\)
∴ The other number (x) = \(\frac{53}{6}\)
Question 11.
Is subtraction associative in rational numbers? Explain with an example.
Solution:
Let \(\frac{1}{2}, \frac{3}{4}, \frac{-5}{4}\) are any 3 rational numbers.
Associative property under subtraction
a – (b – c) = (a – b) – c

∴ L.H.S. ≠ R.H.S.
∴ a – (b – c) ≠ (a – b) – c
∴ Subtraction is not an associative in rational numbers.
![]()
Question 12.
Verify that – (-x) = x for
(i) x = \(\frac{2}{15}\)
(ii) x = \(\frac{-13}{15}\)
Solution:

Question 13.
Write-
(i) The set of numbers which do not have any additive identity
(ii) The rational number that does not have any reciprocal
(iii) The reciprocal of a negative rational number.
Solution:
i) Set of natural numbers ’N’ doesn’t possesses the number ‘0’.
ii) The rational number ‘0’ has no multiplicative inverse.
[ ∵ 1/0 is not defined]
iii) The reciprocal of a negative rational number is a negative rational number.
Ex : Reciprocal of \(\frac{-2}{5}=\frac{-5}{2}\)