AP Inter 2nd Year Physics Study Material Chapter 6 ప్రవాహ విద్యుత్తు

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 6th Lesson ప్రవాహ విద్యుత్తు Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 6th Lesson ప్రవాహ విద్యుత్తు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వాహకంలో ఎలక్ట్రాన్ స్వేచ్ఛా పథమాధ్యమాన్ని నిర్వచించండి.
జవాబు:
ఒక వాహకంలో, ఒక ఎలక్ట్రాన్ రెండు వరుస అభిఘాతాల మధ్య ప్రయాణించిన సరాసరి దూరంను వాహకంలో ఎలక్ట్రాన్ సరాసరి స్వేచ్ఛాపథ మాధ్యమము అంటారు.

ప్రశ్న 2.
ఓమ్ నియమాన్ని తెలిపి, దాని గణిత రూపం రాయండి.
జవాబు:
ఓమ్ నియమము :
స్థిర ఉష్ణోగ్రత వద్ద, వాహకంలో విద్యుత్ ప్రవాహసత్వం (1), దాని రెండు చివరల పొటెన్షియల్ తేడా (V) కు అనులోమానుపాతంలో ఉండును.
∴ I ∝ V ⇒ I = \(\frac{V}{R}\) ⇒ V = IR (గణితరూపం)
ఇక్కడ R ఒక స్థిరాంకం. దీనినే వాహకం నిరోధం అంటారు.

ప్రశ్న 3.
నిరోధకత లేదా విశిష్ట నిరోధంను నిర్వచించండి.
జవాబు:
నిరోధకత లేక విశిష్ట నిరోధం :
ప్రమాణ పొడవు మరియు ప్రమాణ మధ్యచ్ఛేద వైశాల్యం గల వాహకం నిరోధంను నిరోధకత అంటారు.
l = 1, A = 1 ⇒ ρ = \(\frac{R\times1}{1}\) ⇒ ρ =R

ప్రశ్న 4.
ఉష్ణోగ్రత నిరోధ గుణకంను నిర్వచించండి.
జవాబు:
ఉష్ణోగ్రత నిరోధ గుణకం :
ప్రమాణ ఉష్ణోగ్రత పెరుగుదలకు నిరోధకతలోని మార్పుకు, 0°C వద్ద నిరోధకంనకు గల నిష్పత్తిని ఉష్ణోగ్రత నిరోధ గుణకం అంటారు.
α = \(\frac{\mathrm{R}_{\mathrm{t}}-\mathrm{R}_0}{\mathrm{R}_0 \mathrm{t}}\)

ప్రశ్న 5.
ఘటాల మిశ్రిత సంధానం ద్వారా ప్రవహించే విద్యుత్ ఏ సందర్భాల్లో గరిష్ఠంగా ఉంటుంది ?
జవాబు:

1. అన్ని ఘటాల ప్రభావ వి.చా.బ గరిష్ఠం అయిన
2. బాహ్య నిరోధం, అన్ని ఘటాల అంతర నిరోధాల మొత్తమునకు సమానమయినప్పుడు, ఘటాల మిశ్రమ గ్రూపింగ్ విద్యుత్ ప్రవాహం గరిష్ఠం.

ప్రశ్న 6.
ఒక తీగను దాని ద్రవ్యరాశిలో మార్పు లేకుండా తొలి పొడవు రెట్టింపు అయ్యేట్లు సాగదీస్తే, తీగ నిరోధకత ఎలా ప్రభావితం అవుతుంది?
జవాబు:
ఉష్ణోగ్రతలో మార్పు లేకుండా, ఒక పదార్థం పరిమాణంలో మార్పు లేకుండా, తీగ నిరోధకత్వం మారదు.

ప్రశ్న 7.
ప్రామాణిక నిరోధకాల తయారీలో మాంగనీన్ను ఎందుకు ఉపయోగిస్తారు?
జవాబు:
మాంగనీన్ (Cu-84% + Mn – 12% + Ni – 4%) తీగ హెచ్చు నిరోధకత్వం (ρ) మరియు అల్ప ఉష్ణోగ్రత నిరోధ గుణకంను కల్గి ఉండుట వల్ల ప్రమాణ నిరోధాలలో వాడతారు.

ప్రశ్న 8.
కార్బన్ నిరోధకంపై గుర్తించిన రంగుల పట్టీల క్రమం: ఎరుపు, ఎరుపు, ఎరుపు, వెండి, అయితే దాని నిరోధం, సహనం ఎంత?
జవాబు:

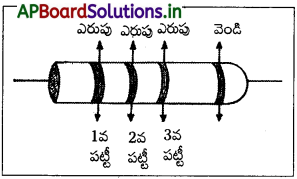
ఎరుపు, ఎరుపు, ఎరుపు గుర్తులతో మార్కు చేయబడిన కార్బన్ నిరోధం = 22 × 10² = 2.2kΩ = 2200Ω
[∵ ఎరుపు క్రమ సంఖ్య = 2 మరియు లబ్ద కారకం = 10²]
కార్బన్ నిరోధకము టోలరెన్స్ = 10²

ప్రశ్న 9.
23 కిలో ఓమ్ల నిరోధం గల కార్బన్ నిరోధకం రంగుల కోడ్ను రాయండి.
జవాబు:
23 కిలో ఓమ్స్ (= 23 × 10³Ω) కార్బన్ నిరోధకం కలర్ కోడ్ వరుసగా ఎరుపు, నారింజ, నారింజ.
[∵ ఎరుపుకు క్రమసంఖ్య 2, నారింజకు 3, నారింజ లబ్ది కారకం 10³]

ప్రశ్న 10.
ఒక వాహకం చివరల మధ్య అనువర్తించిన వోల్టేజిని Vనుంచి 20కి పెంచితే, ఎలక్ట్రాన్ల డ్రిఫ్ట్ వేగం ఎలా మారుతుంది?
జవాబు:

∴ డ్రిఫ్ట్ వేగం రెండు రెట్లు పెరుగును.

ప్రశ్న 11.
సమాన పొడవులు గల రాగి, మాంగనీస్ తీగలు సమాన నిరోధాన్ని కలిగి ఉన్నాయి. వాటిలో ఏది మందమైంది?
జవాబు:
R = \(\frac{\rho \mathrm{A}}{l}\) ⇒ A = \(\frac{Rl}{\rho}\)
ρ_రాగి < ρ_{మాంగనీస్} కావున రాగితీగ, మాంగనీన్ తీగకన్నా మందమైంది.

ప్రశ్న 12.
గృహ ఉపకరణాలను ఎందుకు సమాంతరంగా కలుపుతారు?
జవాబు:
గృహోపకరణ తీగలను సమాంతరంగా కలిపితే, ప్రతి దానిపై వోల్టేజి సమానం. వాని గుండా ప్రవహించి విద్యుత్ (1) గృహోపకరణ సామర్థ్యంపై ఆధారపడును. హెచ్చు సామర్థ్య గృహోపకరణం ఎక్కువ విద్యుత్ను తీసుకొనును. తక్కువ సామర్థ్య గృహోపకరణం తక్కువ విద్యుత్ను తీసుకొనును.
(∵ P = VI or I ∝ P)

ప్రశ్న 13.
లోహాలలో ఎలక్ట్రాన్ డ్రిఫ్ట్ వడి తక్కువ (~ms^-1), ఎలక్ట్రాన్ ఆవేశం కూడా చాలా తక్కువ (~10^-19C), అయినప్పటికీ లోహంతో అధిక పరిమాణంలో విద్యుత్ ప్రవాహాన్ని మనం పొందగలుగుతున్నాం. ఎందుకు?
జవాబు:
లోహం గుండా విద్యుత్ ప్రవాహం, I = n A eV_d.

Aలోహ మధ్యచ్ఛేద వైశాల్యం. ఎలక్ట్రాన్ అవసర వడి V_d(~10⁵ms^-1) జన్వల్పము. ఎలక్ట్రాన్ ఆవేశం e(~1.6 × 10^-19C) కూడా చాలా స్వల్పము. వాహకంలో చాలా స్వేచ్ఛా ఎలక్ట్రాన్లు (~ 10²⁹ m^-3) ఉండుట వల్ల, వాహకంలో ఎక్కువ పరిమాణం ఉన్న విద్యుత్ ప్రవాహంను ఇంకను పొందుతాము.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
10V emf, 3Ω అంతర్నిరోధం గల ఒక బాటరీని R నిరోధానికి సంధానం చేశారు.
i) వలయంలో విద్యుత్ ప్రవాహం 0.5 A అయితే, R విలువను లెక్కించండి.
ii) వలయం మూసి ఉంటే బాటరీ టెర్మినల్ వోల్టేజి ఎంత ?
జవాబు:
ఇచ్చినవి E 10 V, r = 3Ω, I = 0.5 A, R = ?, V = ?

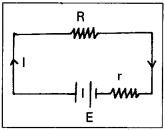
i) E = I (R + r)
లేక R + r = \(\frac{E}{I}=\frac{10}{0.5}\) = 20Ω
⇒ R = 20 – 3 = 17Ω

ii) టెర్మినల్ వోల్టేజి, V = IR
= 0.5 × 17 = 8.5Ω

ప్రశ్న 2.
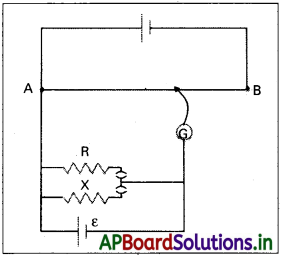
ఒక ఘటం అంతర్నిరోధం తెలుసుకోవడానికి పొటెన్షియోమీటర్ ఎలా ఉపయోగపడుతుందో తెలిపే వలయం రేఖా చిత్రాన్ని గీయండి. దానికి సూత్రాన్ని రాబట్టండి.
జవాబు:

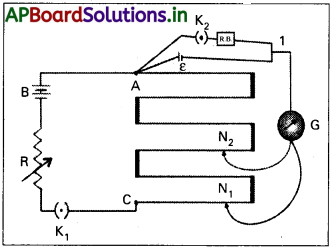
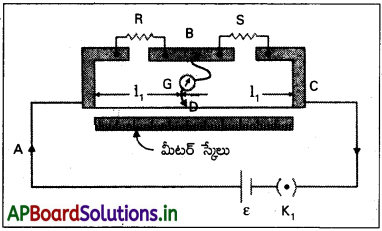
పొటెన్షియోమీటర్తో అంతర్నిరోధం (r) ను కొలుచుట :
1) అంతర్నిరోధం కొలుచు పొటెన్షియోమీటర్ పటంలో చూపబడింది.
2) ఘటం(వి. చా. బ.) అంతర్నిరోధం (r)ను నిర్ణయించుటకు కీ K₂ ద్వారా నిరోధాల పెట్టె సంధానం చేయబడి ఉంటుంది.
3) కీ K తెరిచి, సంతులన పొడవు l₁ (AN₁) పొందుతాము.
అప్పుడు ε = Φ l₁ …………… (1)
4) కీ K₂ ను మూస్తే నిరోధాల పెట్టె (R.B) ద్వారా, ఘటం నుండి విద్యుత్ ప్రవాహం I ప్రవహింపచేస్తుంది.
5) ఘటం, టెర్మినల్ పొటెన్షియల్ తేడా (V) అయినపుడు, సంతులన పొడవు I₂(AN₂) ను పొందితే అప్పుడు

ప్రశ్న 3.
మూడు నిరోధకాలను (i) శ్రేణి, (ii) సమాంతరంగా కలిపినప్పుడు ప్రభావాత్మక నిరోధానికి సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
i) మూడు నిరోధకాలను శ్రేణిలో కలిపినప్పుడు ప్రభావ నిరోధం :

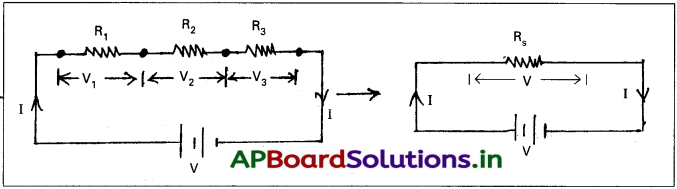
1. మూడు నిరోధకములు R₁, R₂ మరియు R₃ లు శ్రేణిలో పటంలో చూపినట్లు కలుపబడినవి. R₁, R₂ మరియు R₃ల వెంట పొటెన్షియల్ తేడాలు V₁, V₂ మరియు V₃. వాని గుండా ప్రవహించు విద్యుత్ I.
2. R₁, R₂ మరియు R₃ లకు ఓమ్ నియమము అనువర్తిస్తే,
   అప్పుడు V₁ = IR₁, V₂ = IR₂, V₃ = IR₃
3. ఈ శ్రేణిలో, V = V₁ + V₂ + V₃
   IR_s = IR₁ + IR₂ + IR₃ [∵ V = IR_s]
   ∴ R_s = R₁ + R₂ + R₃

ii) మూడు నిరోధాలను సమాంతరంగా కలిపినపుడు ప్రభావ నిరోధం :

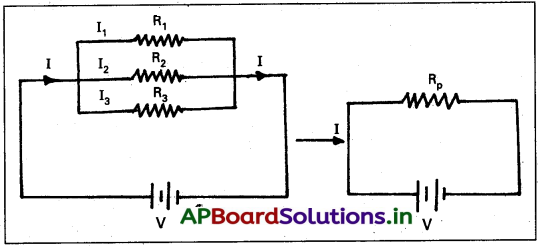
1. మూడు నిరోధకములు R₁, R₂ మరియు R₃ లు సమాంతరంగా పటంలో చూపినట్లు కలుపబడినవి. ప్రతి నిరోధకము వెంట పొటెన్షియల్ తేడా V. వాని గుండా ప్రవహించు విద్యుత్లు I₁, I₂ మరియు I₃.

2. R₁, R₂ మరియు R₃ లకు ఓమ్ నియమము అనువర్తిస్తే, అప్పుడు V = I₁R₁ = I₂R₂ = I₃R₃

ప్రశ్న 4.
ఒక్కొక్కటి E emf, r అంతర్నిరోధం గల m ఘటాలను సమాంతరంగా సంధానం చేశారు. మొత్తం emf, అంతర్నిరోధం ఎంత ? ఘటాల మిశ్రిత సంధానం ద్వారా ఏ సందర్భాలలో విద్యుత్ ప్రవాహం గరిష్టంగా ఉంటుంది?
జవాబు:
ఘటాలను సమాంతరంగా కలిపినప్పుడు :

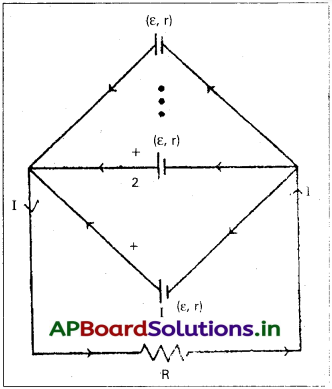
1) అంతర్నిరోధం r, వి.చా.బ. ౬ ఉన్న ఒకే రకమైన m ఘటాలను, బాహ్య నిరోధం R కు సమాంతరంగా పటంలో చూపినట్లు కలిపి ఉన్నాయని భావిద్దాం.

2) ఘటాలు సమాంతరంగా కలుపబడి ఉన్నాయి కావున వాని ప్రభావ అంతర్నిరోధం ను క్రింది సమీకరణం ఇస్తుంది.

3) Rమరియు r లు శ్రేణిలో ఉన్నాయి. వలయంలో మొత్తం
నిరోధం = R + \(\frac{r}{m}\)

4) ఒకే రకమైన ఘటాల సమాంతర సంయోగంలో, వలయంలో ప్రభావ వి.చా. బ. ఒకే ఒక వి.చా. బకు సమానము. ఎందువలన అనగా, ఈ సంయోగంలో ఎలక్ట్రోడుల పరిమాణం మాత్రమే పెరుగును. కాని వి. చా. బ. పెరగదు.

5) ∴ నిరోధంలో విద్యుత్ R = \(\frac{\varepsilon}{\mathrm{R}+\frac{\mathrm{r}}{\mathrm{m}}}=\frac{\mathrm{m} \varepsilon}{\mathrm{mR}+\mathrm{r}}\)

6) బాహ్య నిరోధం, అంతర్నిరోధంతో పోల్చినపుడు విస్మరించ దగిన విలువ కలిగి ఉంటే (R<<r) ఘటాల మిశ్రమ గ్రూపింగులో తీసుకొను విద్యుత్ గరిష్ఠము.

ప్రశ్న 5.
విద్యుత్ నిరోధాన్ని నిర్వచించండి. దాని SI ప్రమాణం రాయండి. కింది సందర్భాలలో వాహక నిరోధం ఎలా మారుతుందో తెల్చండి.
a) వాహకాన్ని దాని పొడవుకు 4 రెట్లు అయ్యేటట్లు సాగదీస్తే,
b) వాహక ఉష్ణోగ్రతను పెంచితే
జవాబు:
విద్యుత్ నిరోధం (R) :
వాహకంలో ఎలక్ట్రాన్ల ప్రవాహంను నిరోధించు ధర్మంను విద్యుత్ నిరోధం అంటారు. నిరోధం SI ప్రమాణం ఓమ్ (Ω).

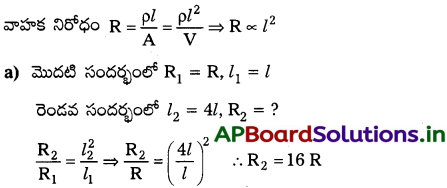
b) ఉష్ణోగ్రతతో నిరోధంలో మార్పు R_t = R₀ (1 + α t)
ఉష్ణోగ్రత పెరిగిన, నిరోధం కూడా పెరుగును.

ప్రశ్న 6.
ఘటానికి శ్రేణిలో కలిపిన నిరోధం సగం అయితే, విద్యుత్ ప్రవాహం రెట్టింపు లేదా రెట్టింపు విలువకు స్వల్పంగా తక్కువ లేదా రెట్టింపు విలువకు స్వల్పంగా ఎక్కువ అవుతుంది. ఎందుకు?
జవాబు:
నిరోధం R ను E వి.చా.బ ఉన్న ఘటంనకు శ్రేణిలో కల్పితే,
విద్యుత్ I = \(\frac{\varepsilon}{R+r}\)

ii) r << \(\frac{R}{2}\) అయితే, విద్యుత్ I’ స్వల్పంగా 2 కన్నా ఎక్కువ.
iii) r, R కన్నా స్వల్పంగా ఎక్కువగా ఉంటే, విద్యుత్ (1) స్వల్పంగా 2 కన్నా తక్కువ.

ప్రశ్న 7.
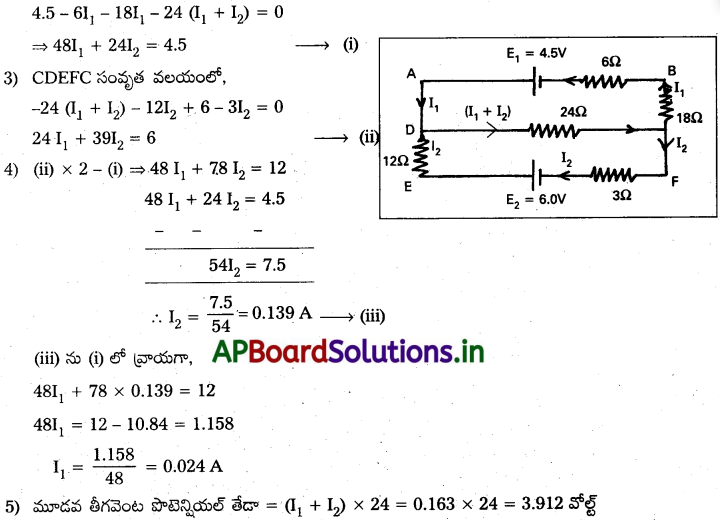
రెండు ఘటాల emfలు, అంతర్నిరోధాలు వరుసగా 4.5V, 6.0V, 6Ω, 3Ω . ఈ ఘటాల రుణ టెర్మినల్స్న 18Ω నిరోధం గల తీగతో ధన టెర్మినలు నన్ను 12Ω నిరోధం గల తీగతో కలిపారు. ఈ తీగల మధ్య బిందువులను 24Ω నిరోధం గల మూడవ తీగ సంధానం చేస్తుంది. కిర్కాఫ్ నియమాలను ఉపయోగించి మూడవ తీగ కొనల మధ్య పొటెన్షియల్ భేదాన్ని కనుక్కోండి.
జవాబు:
1) నెట్వర్క్ వేర్వేరు భుజాల గుండా విద్యుత్ ప్రవాహాలను పటంలో చూపినట్లు భావిద్దాం.
2) ABCDA సంవృత వలయంనకు కిర్కాఫ్ వోల్టేజి. నియమాన్ని అనువర్తిస్తే,

ప్రశ్న 8.
10Ω నిరోధం గల మూడు నిరోధకాలను (i) కనిష్ట నిరోధం, (ii) గరిష్ట నిరోధం వచ్చేటట్లు సంధానం చేశారు. (a) ప్రతీ సందర్భంలో ప్రభావాత్మక నిరోధం, (b) ఆ విధంగా పొందిన కనిష్ఠ, గరిష్ఠ నిరోధాల నిష్పత్తిని గణించండి.
జవాబు:
ప్రతి నిరోధకము యొక్క నిరోధం R = 10Ω
నిరోధకముల సంఖ్య, n = 3

i) మూడు నిరోధకములను సమాంతరంగా కలిపితే, కనిష్ఠ నిరోధం పొందుతాము.
∴ కనిష్ట నిరోధం R_{కనిష్ట} R_p = \(\frac{R}{n}=\frac{10}{3}\)Ω = 3.33Ω
ii) మూడు నిరోధకములను శ్రేణిలో కలిపితే, గరిష్ట నిరోధం పొందుతాము.
∴ గరిష్ట నిరోధం R_{గరిష్ట} = R_s = nR = 3 × 10 = 30Ω

a) కనిష్ట నిరోధం పొందటానికి ప్రభావ నిరోధం,
R_{ప్రభావ} = \(\frac{R}{n}=\frac{10}{3}\) = 3.33Ω (సమాంతరంగా).
గరిష్ట నిరోధం పొందటానికి ప్రభావ నిరోధం,
R_{ప్రభావ} = nR = 3 × 10 = 30Ω (శ్రేణిలో)

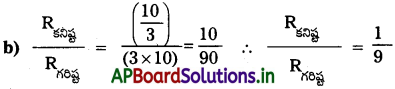
ప్రశ్న 9.
ఒక విద్యుత్ జాలానికి కిర్కాఫ్ నియమాలను తెలపండి. ఈ నియమాలను ఉపయోగించి వీటన్ బ్రిడ్జికి సంతులన నిబంధనను రాబట్టండి. [TS. Mar. 16; Mar. ’14]
జవాబు:
1) కిర్కాఫ్ మొదటి నియమము (సంధి నియమము లేక KCL) :
ఏదైనా సంధి వద్ద విద్యుత్ ప్రవాహాల బీజీయ మొత్తం శూన్యం.
∴ ∑I = 0 (లేక)

సంధి వద్దకు చేరు విద్యుత్ ప్రవాహాల బీజీయ మొత్తము, సంధి నుండి దూరంగా పోవు విద్యుత్ ప్రవాహాల బీజీయ మొత్తమునకు సమానము.

2) కిర్కాఫ్ రెండవ నియమము (సంవృత నియమము లేక KVL) :
ఏదైనా సంవృత వలయం వెంబడి పొటెన్షియల్ల బీజీయ మొత్తం శూన్యం.
∴ ∑(IR) + ∑E = 0

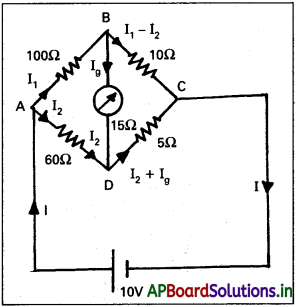
వీటన్ బ్రిడ్జి :
వీటన్ బ్రిడ్జి వలయం R₁, R₂, R₃ మరియు R₄ నిరోధాలు పటములో చూపినట్లు కలుపబడి ఉంటాయి. A మరియు C ల మధ్య ε వి. చా. బ ఉన్న ఘటం, B మరియు D ల మధ్య ఒక గాల్వనామీటర్ పటంలో చూపినట్లు కలుపబడి ఉంటాయి. వేర్వేరు భుజాలలో విద్యుత్ ప్రవాహాలు I₁, I₂, I₃ మరియు I₄. గాల్వనా మీటర్ Gలో విద్యుత్ ప్రవాహము I_g.
కిర్కాఫ్ మొదటి నియమం ప్రకారం
D సంధి వద్ద I₁ – I₃ – I_g = 0 …………. (1)
B సంధి వద్ద I₂ + I_g – I₄ = 0 …………… (2)

కిర్కా రెండవ నియమమును ADBA సంవృత వలయముకు అనువర్తిస్తే,
-I₁R₁ – I_gG + I₂R₂ = 0 లేక
⇒ I₁R₁ + I_gG = I₂R₂ ………… (3)

కిర్కాఫ్ రెండవ నియమమును BCBD సంవృత G వలయంకు అనువర్తిస్తే,
-I₃R₃ + I₄R₄ + I_gG = 0
⇒ I₃R₃ – I_gG = I₄R₄ ……….. (4)

గాల్వనా మాపకం శూన్య అపవర్తనంను చూపితే, బిందువులు D మరియు B లు ఒకే పొటెన్షియల్ చూపును.

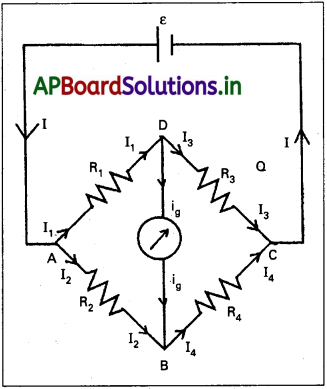
I_g = 0.
ఈ విలువను (1), (2), (3) మరియు (4)లలో ప్రతిక్షేపించగా
I₁ = I₃ ……….. (5)
I₂ = I₄ ……….. (6)
I₁R₁ = I₂R₂ ……….. (7)
I₃R₃ = I₄R₄ ……….. (8)

సమీకరణం (7) ను (8) చే భాగించగా

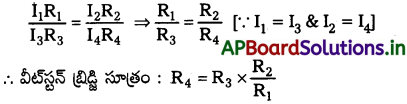
ప్రశ్న 10.
పొటెన్షియోమీటర్ పనిచేసే సూత్రాన్ని తెలపండి. పొటెన్షియోమీటర్ను ఉపయోగించి రెండు ప్రాథమిక ఘటాల emf లను ఎలా పోలుస్తారో వలయం రేఖా చిత్రం సహాయంతో వివరించండి. [AP. Mar: ’17; AP. Mar ’16]
జవాబు:
పొటెన్షియోమీటర్ పనిచేయు సూత్రము : పొటెన్షియోమీటర్ తీగ పొడవు వెంబడి పొటెన్షియల్ తేడా, తీగ పొడవుకు | అనులోమానుపాతంలో ఉండును. (లేక) ఏకరీతి తీగ గుండా నిలకడ విద్యుత్ ప్రవహిస్తే, ప్రమాణ పొడవుకు పొటెన్షియల్ తగ్గుదల లేక పొటెన్షియల్ నతిక్రమము స్థిరము.
i.s.ε ∝ l
⇒ ε = Φl. ఇక్కడ Φ పొటెన్షియల్ నతిక్రమము.

రెండు ఘటాల వి.చా.బ. లు ε₁ మరియు ε₁ లను పోల్చుట :

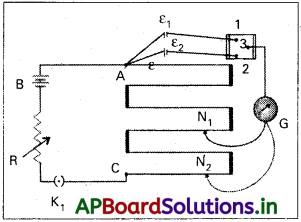
1. పొటెన్షియోమీటర్తో పోల్చవలసిన రెండు ఘటాల విచాబ E₁ మరియు E₂ లు పటంలో చూపబడినవి.
2. 1, 2, 3 బిందువుల గుర్తులు ఒక ద్విమార్గ కీను తెల్పును.
3. కీ మొదటి స్థానంలో 1, 3 లు గాల్వనామాపకం ద్వారా ఘటం ε₁ కి కలుపబడినవి.
4. జాకీని తీగవెంట A నుండి N₁ కు జరిపిన, గాల్వనా మీటర్
   అపవర్తనం సున్న. సంతులన పొడవు AN₁ = l₁.
   అప్పుడు ε₁ ∝ l₁ ⇒ ε₁ = Φl₁ …………… (1)
5. ఇదే విధంగా మరొక ఘటం ε₂, సంతులన పొడవు AN₂ = l₂.
   అప్పుడు ε₂ ∝ l₂ ⇒ ε₂ = Φl₂ …………… (2)
6. \(\frac{\text { (1) }}{(2)} \Rightarrow \frac{\varepsilon_1}{\varepsilon_2}=\frac{l_1}{l_2}\)

ప్రశ్న 11.
పొటెన్షియోమీటర్ పనిచేసే సూత్రాన్ని తెలపండి. పొటెన్షియోమీటర్ను ఉపయోగించి ఇచ్చిన ఘటం అంతర్నిరోధాన్ని ఎలా కనుక్కోవచ్చో వలయం రేఖా చిత్రం సహాయంతో వివరించండి. [TS. Mar. 17; AP & TS. Mar. 15]
జవాబు:
పొటెన్షియోమీటర్ పనిచేయు సూత్రము :
పొటెన్షియోమీటర్ తీగ పొడవు వెంబడి పొటెన్షియల్ తేడా, తీగ పొడవుకు అనులోమానుపాతంలో ఉండును. (లేక) ఏకరీతి తీగ గుండా నిలకడ విద్యుత్ ప్రవహిస్తే, ప్రమాణ పొడవుకు పొటెన్షియల్ తగ్గుదల లేక పొటెన్షియల్ నతిక్రమము స్థిరము.
i.e. ε ∝ l ⇒ ε = Φl ఇక్కడ పొటెన్షియల్ నతిక్రమము.

పొటెన్షియోమీటర్తో అంతర్నిరోధం (r) ను కొలుచుట :

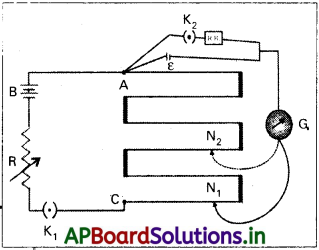
1) అంతర్నిరోధం కొలుచు పొటెన్షియోమీటర్ పటంలో చూపబడింది.

2) ఘటం (వి.చా.బ. E) అంతర్నిరోధం (r) ను నిర్ణయించుటకు కీ K ద్వారా నిరోధాల పెట్టె సంధానం చేయబడి ఉంటుంది.

3) కీ K₂ తెరిచి, సంతులన పొడవు I₁ (AN₁) పొందుతాము.
అప్పుడు ε = Φ l₁ ………… (1)

4) కీ K ను మూస్తే నిరోధాల పెట్టె (R.B) ద్వారా, ఘటం నుండి విద్యుత్ ప్రవాహం I ప్రవహింపచేస్తుంది.

5) ఘటం, టెర్మినల్ పొటెన్షియల్ తేడా (V) అయినపుడు, సంతులన పొడవు I₂(AN₂) ను పొందితే అప్పుడు

ప్రశ్న 12.
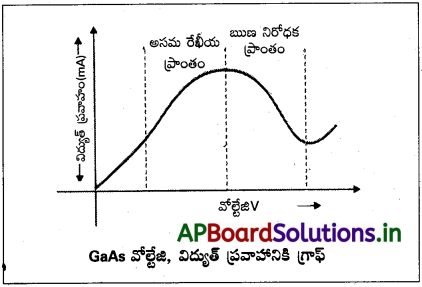
GaAs కు అనువర్తించిన వోల్టేజి, విద్యుత్ ప్రవాహానికి గ్రాఫ్ను చూపండి. గ్రాఫ్లో (i) రేఖీయంగా లేని ప్రాంతం, (ii) ఋణాత్మక నిరోధ ప్రాంతాలను గుర్తించండి.
జవాబు:
V మరియు I ల మధ్య సంబంధం ఒకే విధంగా ఉండదు. ఒకే విద్యుత్ ప్రవాహం కు ఒకదాని కన్నా ఎక్కువ V విలువలు ఉండును. ఇటువంటి పదార్థ స్వభావంను GaAs (i.e., ఒక కాంతి ఉద్గార్గి డయోడ్) చూపును.

ప్రశ్న 13.
ఒక విద్యార్థి దగ్గర సమానమైన పొడవు, వ్యాసాలు గల ఇనుము, రాగి రెండు తీగలు కలవు. అతడు ఆ రెండు తీగలను మొదట శ్రేణిలో కలిపి ఆ సంధానం ద్వారా విద్యుత్ ప్రవాహాన్ని క్రమేపీ పెంచాడు. ఆ తరువాత ఆ రెండు తీగలను సమాంతరంగా కలిపి పై విధంగా ప్రవాహాన్ని పంపడాన్ని పునరావృతం చేశాడు. ప్రతీ సందర్భంలోను ఏ తీగ మొదట వెలుగును ఇస్తుంది?
జవాబు:
1) శ్రేణి సంధానంలో, ఇనుము మరియు రాగితీగ గుండా ఒకే విద్యుత్ ప్రవహించును. ఉష్ణ ఉత్పత్తి రేటు, P ∝ I² R లేక P ∝ R. (∵ I = స్థిరం). ఒకే పొడవు, ఒకే వ్యాసము ఉన్న తీగలలో, ఇనుము తీగ నిరోధము, రాగి తీగ కన్నా ఎక్కువగా ఉండును. కావున ఇనుము తీగలో, ఉష్ణ ఉత్పత్తి రేటు క్రమముగా పెరుగును. శ్రేణి సంధానములో ఇనుము మొదట వెలుగును.

2) ఇనుము మరియు రాగి తీగల సమాంతర సంధానంలో, వాని వెంట ఒకే పొటెన్షియల్ తేడా (V) ఉండును. ఉష్ణ ఉత్పత్తి రేటు, P = \(\frac{V^2}{R}\) లేక P ∝ \(\frac{1}{R}\) (∵ V = స్థిరం), ఒకే పొడవు, ఒకే వ్యాసము ఉన్న తీగలలో, ఇనుము తీగ నిరోధం, రాగి, తీగకన్నా ఎక్కువగా ఉండును. కావున. రాగితీగలో, ఉష్ణ ఉత్పత్తి రేటు ఎక్కువ. సమాంతర సంధానంలో రాగితీగ మొదట వెలుగును.

ప్రశ్న 14.
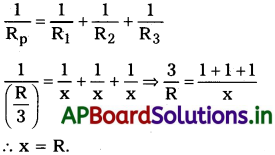
సర్వ సమమైన మూడు నిరోధకాలను సమాంతరంగా కలిపినప్పుడు వలయం మొత్తం నిరోధం R/3. ప్రతీ నిరోధం విలువను కనుక్కోండి.
జవాబు:
మూడు నిరోధాలు ఒకే విధంగా ఉండును.
కావున R₁ = R₂ = R₃ = X (అనుకుందాము)
సమాంతర సంధానంలో మొత్తం నిరోధం, R_p = \(\frac{R}{3}\)
మూడు ఒకే విధమైన నిరోధాలు సమాంతరంగా కలుపబడితే, అప్పుడు

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఒక విద్యుత్ వలయంలో ఉత్పత్తి అయిన ఉష్ణం ఏ పరిస్థితుల్లో ఆ వలయం నిరోధానికి a) అనులోమానుపాతంలో,b) విలోమానుపాతంలో ఉంటుంది ? ఈ రెండు సందర్భాల్లో ఉత్పత్తి అయిన ఉష్ణ పరిమాణాల నిష్పత్తిని గణించండి.

జవాబు:
విద్యుత్ ప్రవాహం వల్ల ఉష్ణ ఉత్పత్తికి సమాసము :
నిరోధం ఉన్న వాహకం AB ను భావిద్దాం.
AB వెంట ప్రయోగించిన పొటెన్షియల్ తేడా = V
AB గుండా పోవు విద్యుత్ = I
విద్యుత్ ప్రవహించిన కాలం = t

∴ t కాలంలో A నుండి B కు ప్రవహించిన మొత్తం ఆవేశం q = It.

పొటెన్షియల్ తేడా నిర్వచనం ప్రకారం, A నుండి B కు ప్రమాణ ఆవేశంను తీసుకొని పోవటానికి జరిగిన పని = V.
A నుండి B కు “q” ఆవేశంను తీసుకుపోవుటలో జరిగిన పని
W = V × q = VIt = I²Rt (∵ V = IR)
ఈ జరిగిన పనిని, విద్యుత్ జరిగిన పని అంటారు. ఈ విద్యుత్ జరిగిన పని ఉష్ణరూపంలో వెలువడును. వెలువడిన ఉష్ణ ఉత్పత్తి
H = W = I²Rt’ జౌల్
ఇదియే జౌల్స్ ఉష్ణ నియమ నిర్వచనం.
a) విద్యుత్ వలయంలో ప్రవహించిన ఉష్ణం వెలువడును.
i.e., H₁ ∝ R

b) ఒకే పొటెన్షియల్ తేడాను, విద్యుత్ వలయం వెంట ప్రయోగిస్తే, ఉష్ణం వెలువడును.
i. e., H₂ ∝ \(\frac{1}{R}\)

ప్రశ్న 2.
A, B అనే రెండు లోహపు తీగలను సమాంతరంగా సంధానం చేశారు. A అనే తీగ L పొడవు, వ్యాసార్థాన్ని కలిగి ఉంటే, B తీగ 2L పొడవు, 2. వ్యాసార్థాన్ని కలిగి ఉంది. సమాంతర సంధానం మొత్తం నిరోధానికి A తీగ నిరోధానికి గల నిష్పత్తిని గణించండి.
జవాబు:

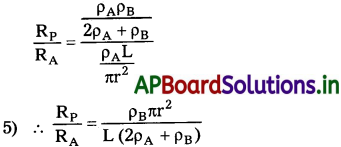
2) A మరియు B తీగల సమాంతర సంధానంలో, మొత్తం నిరోధం.

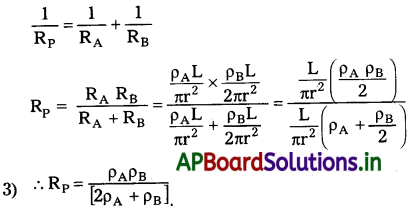
4) సమాంతర సంధానంలో మొత్తం నిరోధంనకు తీగ నిరోధం A కు గల నిష్పత్తి

ప్రశ్న 3.
ఒక ఇంట్లో ఒక్కొక్కటి 100 W రేటింగ్ ఉన్న 3 విద్యుత్ బల్బులు రోజుకు 4 గంటలు వెలుగుతున్నాయి. అలాగే 20W రేటింగ్ ఉన్న ఆరు ట్యూబ్లెట్లు రోజుకు 5 గంటలు వెలుగుతున్నాయి. 400 W రిఫ్రిజిరేటర్ రోజుకు 10 గంటలు చొప్పున వినియోగిస్తే నెలకు 30 రోజుల చొప్పున ఒక యూనిట్కు రూ.4.00 వంతున విద్యుత్ బిల్లును లెక్కించండి.
జవాబు:
ఒక ఇంట్లో ఉన్న బల్బుల సంఖ్య, N = 3
ప్రతి బల్బుపై సామర్థ్య రేటు, P = 100 W
వెలిగించిన కాలం, t = 4 గం||లు

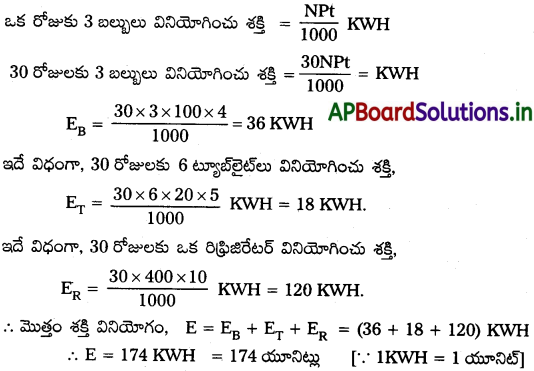
1 యూనిట్ ఖరీదు = రూ.4.00/-
174 యూనిట్ల ఖరీదు = యూనిట్ల సంఖ్య X ఒక యూనిట్ ఖర్చు = 174 × 4 = రూ.696/-
ఆ ఇంటికి ఒక నెలకు విద్యుత్ బిల్లు = రూ. 696/–.

ప్రశ్న 4.
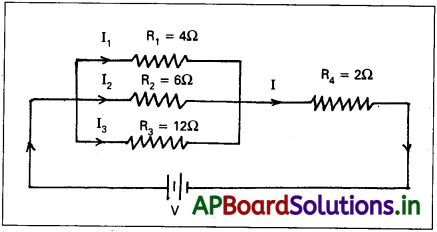
4 ఓమ్లు, 6 ఓమ్లు, 12 ఓమ్లు గల మూడు నిరోధకాలను సమాంతరంగా సంధానం చేశారు. ఈ నిరోధకాల శ్రేణి సంయోగాన్ని 2 ఓమ్ల నిరోధానికి, 6Vల బ్యాటరీకి శ్రేణిలో సంధానం చేశారు. వలయం రేఖాచిత్రాన్ని గీసి, కింది మూడు సందర్భాలలోని విలువలను లెక్కించండి.
a) ప్రధాన వలయంలోని విద్యుత్ ప్రవాహం
b) సమాంతర సంధానంలో ప్రతీ నిరోధకం ద్వారా ప్రవహించే విద్యుత్.
c) 2 ఓమ్ల నిరోధకం ఉపయోగించిన పొటెన్షియల్ భేదం, సామర్థ్యం.
జవాబు:
ఇచ్చిన దత్తాంశమునకు వలయ పటం క్రింద ఇవ్వబడింది.

ప్రశ్న 5.
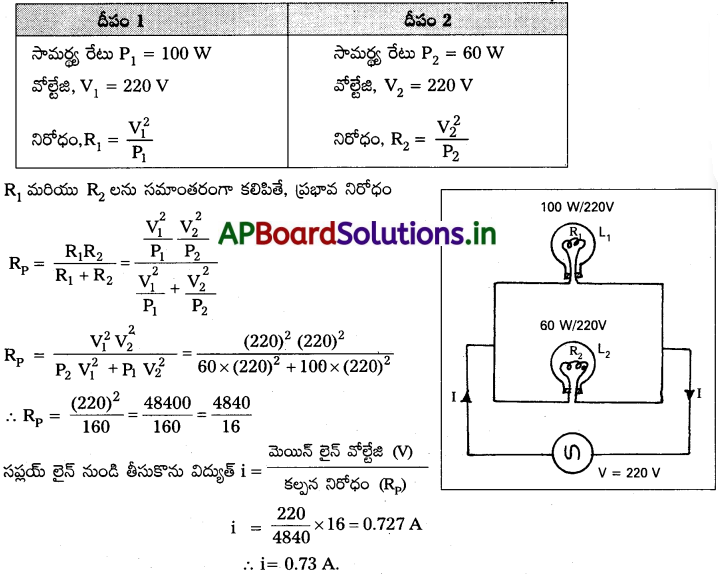
220 V వద్ద 100 W, 220 V వద్ద 60 W రేటింగ్లు గల రెండు బల్బులను 220 V సరఫరాకు సమాంతరంగా కలిపారు. సరఫరా తీగల నుంచి ఎంత విద్యుత్ ప్రవాహాన్ని తీసుకుంటుంది?
జవాబు:
దత్తాంశము

ప్రశ్న 6.
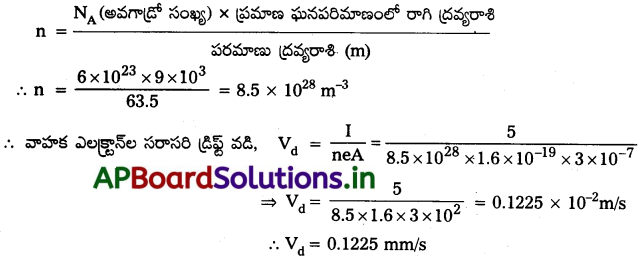
3.0 × 10^-7 m² మధ్యచ్ఛేద వైశాల్యం, 5 A విద్యుత్ ప్రవహిస్తున్న రాగి తీగలోని వహన ఎలక్ట్రాన్ల సరాసరి డ్రిఫ్ట్ వడిని అంచనా వేయండి. ప్రతీ రాగి పరమాణువు ఒక వహన ఎలక్ట్రాను సమకూరుస్తుంది అని భావించండి. రాగి సాంద్రత 9.0 × 10³ kg/m³, దాని పరమాణు ద్రవ్యరాశి 63.5u.
జవాబు:
రాగితీగ మధ్యచ్ఛేద వైశాల్యం A = 3 × 10^-7 m² రాగి తీగ ద్వారా విద్యుత్, I = 5 A
ఎలక్ట్రాన్ ఆవేశం, e = 1.6 × 10^-19C
ఎలక్ట్రాన్ల వాహక సాంద్రత = ప్రమాణ ఘనపరిమాణంలో పరమాణువుల సంఖ్య

ప్రశ్న 7.
పై లెక్కలో వచ్చిన డ్రిఫ్ట్ వడిని కింది వాటితో పోల్చండి.
i) సాధారణ ఉష్ణోగ్రతల వద్ద రాగి పరామణువుల ఉష్ణయవడి (Thermal speed)
ii) డ్రిఫ్ట్ గమనానికి కారణమై, తీగ వెంబడి వ్యాపనం (propagation) చెందే విద్యుత్ క్షేత్రం వడి.
జవాబు:
i) T ఉష్ణోగ్రత వద్ద, రాగి పరమాణు ద్రవ్యరాశి (M) ఉష్ణ వడిని క్రింది సమీకరణం నుండి రాబట్టవచ్చును.

∴ ఎలక్ట్రాన్ డ్రిఫ్ట్ వడి (V_d) = 1.047 × 10^-8 = సాధారణ ఉష్ణోగ్రత వద్ద ఉష్ణవడి × 10^-8 రెట్లు

ii) వాహకం వెంట విద్యుత్ క్షేత్రం, విద్యుదయస్కాంత తరంగ వడితో ప్రయాణించును.

∴ అపసర వడిని C తో పోల్చిన, 10^-11 రెట్లు తక్కువగా ఉండును.

లెక్కలు Problems

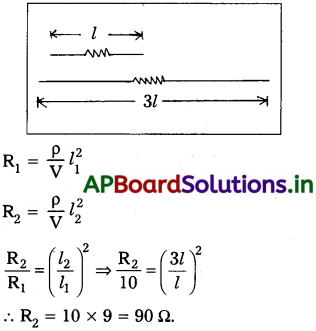
ప్రశ్న 1.
10Ω మందమైన ఒక తీగను దాని పొడవు మూడు రెట్లు అయేటట్లు సాగదీశారు. సాగదీయడం వల్ల దాని సాంద్రతలో ఎటువంటి మార్పు లేదని భావించి సాగ దీసిన తీగ నిరోధం కనుక్కోండి.
సాధన:
ఇచ్చినది R₁ = 10Ω
l₁ = l
l₂ = 3l
R₂ = ?

ప్రశ్న 2.
4R నిరోధం గల ఒక తీగను వృత్తాకారంలో వంచారు. దాని వ్యాసం కొనల మధ్యగల ప్రభావాత్మక నిరోధం ఎంత? [TS. Mar. 16; Mar. ’14]
సాధన:
పొడవాటి తీగ నిరోధం = 4R
సగం తీగ నిరోధం = \(\frac{4R}{2}\) = 2R

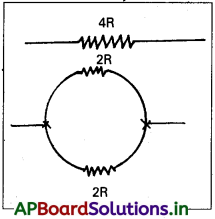
సగం పొడవున్న, రెండు తీగల చివరలు పటంలో చూపినట్లు కలిపితే వృత్తం ఏర్పడుతుంది. వ్యాసం వెంట తీగ చివరల మధ్య ప్రభావ నిరోధము,

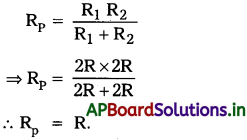
ప్రశ్న 3.
15 Vm^-1 విద్యుత్ క్షేత్రాన్ని ఒక వాహకం కొనల మధ్య అనువర్తించినప్పుడు, ఆ వాహకం 2.5 × 10⁶ Am^-2 విద్యుత్ ప్రవాహ- సాంద్రతను కలిగి ఉంది. ఆ వాహకం నిరోధకతను కనుక్కోండి.
సాధన:
విద్యుత్ ప్రవాహ సాంద్రత = J = \(\frac{I}{R}\)
= 2.5 × 10^-6 Am^-2
ప్రయోగించిన విద్యుత్ క్షేత్రం, E = 15 Vm^-1
వాహకం విశిష్టోష్ణం, ρ = \(\frac{E}{J}=\frac{15}{2.5\times10^6}\)
∴ ρ = 6 × 10^-6 Ωm.

ప్రశ్న 4.
5% సహనంతో 350ml ల నిరోధాన్ని కలిగి ఉన్న ఒక నిరోధకం రంగుల కోడ్ ఏమిటి?
సాధన:
ఒక నిరోధకము యొక్క నిరోధం = 350 mΩ
= 350 × 10^-3 Ω
= 35 × 10^-2 Ω

సహన శీలత (Tolerance) = 5%
మొదటి సార్థకసంఖ్య (3), మొదటి పట్టీను సూచించును.
రెండవ సార్థకసంఖ్య (5), రెండవ పట్టీను సూచించును.
మూడవ సార్థకసంఖ్య (10^-2) మూడవ పట్టీను సూచించును.

ప్రశ్న 5.
మీకు 8Ω నిరోధకం ఇచ్చారు. 6Ω నిరోధాన్ని పొందడానికి దానికి, 120 Ωm నిరోధకతను కలిగి ఉన్న ఎంత పొడవుగల తీగను సమాంతరంగా కలపాలి?
సాధన
నిరోధకము యొక్క నిరోధం R = 8Ω

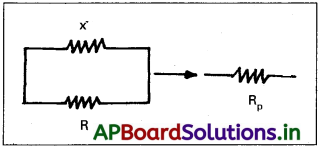
తీగ విశిష్ట నిరోధం ρ = 120
1 పొడవున్న నిరోధంను Rకు సమాంతరంగా కలిపితే,
ప్రభావ నిరోధం, R_p = 6Ω

ప్రశ్న 6.
ఒక బ్యాటరీకి 3Ω, 6Ω, 9Ω మూడు నిరోధకాలను సంధానం చేశారు. ఒకవేళ a) అవన్నీ సమాంతరంగా కలిపినప్పుడు, b) అవన్నీ శ్రేణిలో కలిపినప్పుడు వాటిలోని ఏ నిరోధకంలో సామర్థ్య దుర్వ్యయం గరిష్టంగా ఉంటుంది. కారణాలను ఇవ్వండి.
సాధన:
ఇచ్చినవి R₁ = 3Ω, R₂ = 6Ω, R₃ = 9Ω

a) సమాంతరంగా కలిపిన నిరోధాల ప్రభావ నిరోధము

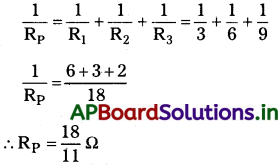
∴ సమాంతర సంయోగంలో దుర్వ్యయ సామర్థ్యము,

b) శ్రేణిలో ప్రభావ నిరోధం,
R_s = R₁ + R₂ + R₃ = 3 + 6 + 9 = 18Ω
∴ శ్రేణిలో దుర్వ్యయ సామర్థ్యం
P_S ∝ R_S ⇒ P_S ∝ 18 → (2)

(1) మరియు (2) సమీకరణాల నుండి, దుర్వ్యయ సామర్థ్యం శ్రేణిలో గరిష్టం మరియు సమాంతరంగా కనిష్టం.

కారణాలు :

1. శ్రేణి సంధానంలో, P ∝ R మరియు V ∝ R. కావున దుర్వ్యయ సామర్థ్యం (P) మరియు పొటెన్షియల్ భేదం (V) ఎక్కువ. ఎందుకనగా ప్రతినిరోధకం వెంట విద్యుత్ ప్రవాహం సమానము.
2. సమాంతర సంధానంలో P ∝ \(\frac{1}{R}\) మరియు I ∝ \(\frac{1}{R}\) కావున దుర్వ్యయ సామర్థ్యం (P) మరియు పొటెన్షియల్ భేదము (V) తక్కువ. ఎందుకనగా ప్రతినిరోధకము వెంట వోల్టేజి సమానము.

ప్రశ్న 7.
ఒక వెండి తీగ 27.5°C వద్ద 2.1Ω నిరోధాన్ని, 100°C వద్ద 2.7Ω నిరోధాన్ని కలిగి ఉంది. వెండి ఉష్ణోగ్రత నిరోధకత గుణకం కనుక్కోండి.
సాధన:
వెండి తీగకు (సిల్వర్) R₁ = 2.1Ω, t₁ = 27.5°C
R₂ = 2.7Ω,
t₂ = 100°C, α = ?

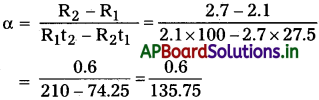
∴ ఉష్ణోగ్రత నిరోధకత గుణకం a = 0.443 × 10^-2 °C

ప్రశ్న 8.
ఒక విద్యుత్సాహక తీగ పొటెన్షియల్ భేదాన్ని స్థిరంగా ఉంచి, దాని పొడవు రెట్టింపు అయ్యేటట్లు సాగదీస్తే, ఎలక్ట్రాన్ల డ్రిఫ్ట్ వడి ఎన్ని రెట్లు మారుతుంది?
సాధన:

∴ ఎలక్ట్రాన్స్ డ్రిఫ్ట్ వడి 2 రెట్లు అగును.

ప్రశ్న 9.
25,200 రేటింగ్ ఉన్న రెండు 120 V బల్బులను శ్రేణిలో కలిపారు. వాటిలో ఒక బల్బు దాదాపు వెంటనే కాలిపోయింది. ఏ బల్బు కాలిపోయింది? ఎందుకు?
సాధన:
మొదటి బల్బుకు
P₁ = 25W, V₁ = 120V


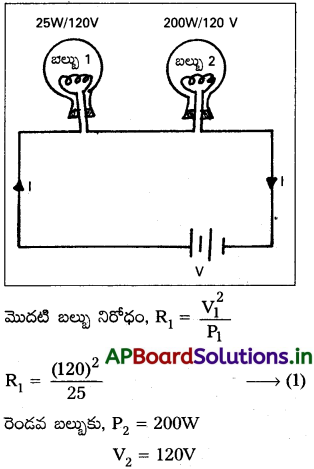
రెండు బల్బులు ఒకే వోల్టేజిని కలిగి ఉన్నప్పటికి, R₁ > R₂ అగుట వల్ల 25 W బల్బు తక్షణం కాలి పోతుంది.

ప్రశ్న 10.
ఒక స్థూపాకార లోహపు తీగను దాని పొడవు 5% పెరిగేటట్లు సాగదీశారు. దాని నిరోధంలో కలిగే మార్పు శాతం కనుక్కోండి.
సాధన:

ప్రశ్న 11.
ఒక పదార్థంతో చేసిన A, B అనే రెండు తీగలు సమాన పొడవులు కలిగి ఉన్నాయి. వాటి మధ్యచ్ఛేద వైశాల్యాల నిష్పత్తి 1: 4, ఆ రెండు తీగల కొనల మధ్య స్థిరమైన వోల్టేజిని అనువర్తిస్తే, వాటిలో ఉత్పత్తి అయ్యే ఉష్ణదాశుల నిష్పత్తి ఎంత?
సాధన:
ఇచ్చినవి l_A = l_b, ρ_A = ρ_B, V_A = V_B, A_A : B_B = 1 : 4
తీగలో జనించు ఉష్ణరేటు,

A మరియు B తీగలకు ఒకే V, ρ, l లు ఉంటే
H ∝ A (మధ్యచ్ఛేద వైశాల్యం)
A మరియు B రెండు తీగలకు,

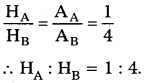
ప్రశ్న 12.
స్థిరమైన వోల్టేజి జనకానికి సమాంతరంగా కలిపిన రెండు బల్బుల నిరోధాల నిష్పత్తి 1 : 2. వాటిలో దుర్వ్యయం అయ్యే సామర్థ్యాల నిష్పత్తి ఎంత ?
సాధన:
ఇచ్చినవి R₁ : R₂ = 1 : 2
సమాంతర సంధానంలో దుర్వ్యయ సామర్థ్యం,
P = \(\frac{V^2}{R}\)
⇒ P = \(\frac{1}{R}\) [∵ V = స్థిరాంకము]
రెండు బల్బులలో దుర్వ్యయ సామర్ధ్యాల నిష్పత్తి.
\(\frac{P_1}{P_2}=\frac{R_2}{R_1}=\frac{2}{1}\)
∴ P₁ : P₂ = 2 : 1.

ప్రశ్న 13.
5m పొడవు గల పొటెన్షియోమీటర్ తీగ కొనల మధ్య 6 V పొటెన్షియల్ భేదం కొనసాగించారు. పొటెన్షియో మీటర్ తీగ 180 cm పొడవు వద్ద సంతులన స్థానాన్ని ఇస్తే, ఆ ఘటం emf కనుక్కోండి. [AP. Mar.’17; AP. Mar.’16]
సాధన:
పొటెన్షియోమీటర్ తీగ పొడవు, L = 5m
పొటెన్షియల్ భేదము, V = 6 వోల్ట్
పొటెన్షియల్ నతిక్రమము,
Φ = \(\frac{V}{L}=\frac{6}{5}\) = 1.2V/M.
సంతుల పొడవు, l = 180 cm = 1.80 m
ఘటం వి.చా. బ., E = Φl
= 1.2 × 1.8 = 2.16V.

ప్రశ్న 14.
2.5 Vemf, r అంతర్నిరోధం గల ఒక బ్యాటరీని 1 ఓమ్ నిరోధం గల అమ్మీటర్ ద్వారా 45 ఓమ్ నిరోధానికి శ్రేణిలో కలిపారు. అమ్మీటర్ 50 m విద్యుత్ ప్రవాహం చూపిస్తుంది. వలయం రేఖా చిత్రాన్ని గీయండి, r విలువను కనుక్కోండి. [TS. Mar: ’17]
సాధన:
ఇచ్చిన దత్తాంశ వలయ పటం కింద చూపబడింది.

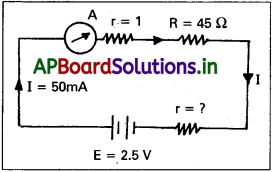
E = 2.5
R = 45 Ω
r_A = 1A
i = 50 mA
r = ?
E = I(R + r_A + r)
2.5 = 50 × 10^-3 (45 + 1 + r)

ప్రశ్న 15.
ఒక తీగ మధ్యచ్ఛేదం ద్వారా పోయే విద్యుదావేశ పరిమాణం q(t) = at² + bt + c. a, b, c లకు మితీయ ఫార్ములాలు రాయండి. SI ప్రమాణాలలో a, b, c విలువలు వరుసగా 6, 4, 2 అయితే, t = 6 సెకన్ల వద్ద విద్యుత్ ప్రవాహ విలువను కనుక్కోండి.
సాధన:
తీగ గుండా ప్రవహించు ఆవేశం q(t) = at²+bt +c
సజాతీయ సూత్రం ప్రకారం,
q(t) = at² మితిఫార్ములా
IT = aT²
q(t) మితిఫార్ములా = bt మితిఫార్ములా
IT = bT
∴ b మితిఫార్ములా = I
q(t) మితిఫార్ములా = C మితిఫార్ములా
IT = C మితి ఫార్ములా
∴ C మితి ఫార్ములా =IT
విద్యుత్ ప్రవాహం, I = \(\frac{dq(t)}{dt}\)
= \(\frac{d}{dt}\) [at² + bt + c]
= 2at + b
ఇక్కడ a = 6 మరియు b = 4
⇒ I = 12t + 4
∴ t = 6 సె. వద్ద విద్యుత్ ప్రవాహం
I = 12 × 6 + 4 = 76A.

అభ్యాసాలు Textual Exercises

ప్రశ్న 1.
ఒక కారు సంచాయక ఘటమాల (storage battery) emf 12 V, అంతర్నిరోధం 0.40. బ్యాటరీ నుంచి పొందగలిగే గరిష్ట విద్యుత్ ప్రవాహం ఎంత?
సాధన:
E = 12 V, r = 0.4 Ω
గరిష్ట విద్యుత్, I_max = \(\frac{E}{r}=\frac{12}{0.4}\) = 30A

ప్రశ్న 2.
10V emf, 3Ω అంతర్నిరోధకం గల ఒక బ్యాటరీని నిరోధకానికి సంధానం చేశారు. వలయంలోని విద్యుత్ ప్రవాహం 0.5 A అయితే, ఆ నిరోధకం నిరోధం ఎంత ? వలయం మూసి (closed) ఉన్నప్పుడు బ్యాటరీ టెర్మినల్ వోల్టేజిని కనుక్కోండి. [TS. Mar. 15]
సాధన:
E = 10 V, r = 3Ω, I = 0.5 A, R = ?, V = ?
I = \(\frac{E}{(R+r)}\) లేక (R + r) = \(\frac{E}{I}=\frac{10}{0.5}\) = 20
లేక R = 20 – r = 20 – 3 = 17Ω
అంత్య వోల్టేజి, V = IR = 0.5 × 17 = 8.5 Ω.

ప్రశ్న 3.
a) 1Ω, 2Ω, 3Ω ల మూడు నిరోధకాలను శ్రేణిలో సంధానం చేశారు. సంయోగం మొత్తం నిరోధం ఎంత ?
సాధన:
R₁ = 1 Ω, R₂ = 2 Ω, R₃ = 3 Ω, V = 12 V
శ్రేణిలో, మొత్తం నిరోధం R_S = R₁ + R₂ + R₃
= 1+ 2+ 3 = 6Ω.

b) ఈ సంయోగాన్ని ఉపేక్షించదగిన అంతర్నిరోధం, 12 Vemf గల బ్యాటరీకి కలిపితే, ప్రతి నిరోధకం కొనల మధ్య గల పొటెన్షియల్ పాతాన్ని పొందండి.
సాధన:
వలయంలో ప్రవహించు విద్యుత్ I = \(\frac{V}{R_S}=\frac{12}{6}\) = 2A
R₁ వెంట పొటెన్షియల్ = IR₁ = 2 × 1 = 2V
R₂ వెంట పొటెన్షియల్ = IR₂ = 2 × 2 = 4V
R₃ వెంట పొటెన్షియల్ = IR₃ = 2 × 3 = 6V

ప్రశ్న 4.
a) మూడు నిరోధకాలు 2 Ω, 4 Ω, 5 Ω లను సమాంతరంగా కలిపారు. ఈ సంయోగం మొత్తం నిరోధం ఎంత?
సాధన:
R₁ = 2 Ω, R₂ = 4 Ω, R₃ = 5 Ω, V = 20V
సమాంతర సంధానంలో, మొత్తం నిరోధం = R_p

b) ఈ నిరోధకాల సంయోగాన్ని ఉపేక్షించదగిన అంతర్నిరోధం, 20 Vemf గల బ్యాటరీకి కలిపితే, ప్రతీ నిరోధకం గుండా ప్రవహించే విద్యుత్, బ్యాటరీ నుంచి తీసుకొన్న మొత్తం విద్యుత్ ప్రవాహాన్ని కనుక్కోండి.
సాధన:
R ద్వారా విద్యుత్ = \(\frac{V}{R_1}=\frac{20}{2}\) = 10A

ప్రశ్న 5.
గది ఉష్ణోగ్రత వద్ద (27.0°C) ఒక వేడెక్కే తీగ (heating element) నిరోధం 100 Ω. ఆ వేడెక్కే తీగ నిరోధాన్ని 117 Ω గా గుర్తించినట్లయితే దాని ఉష్ణోగ్రత ఎంత? ఆ నిరోధక పదార్థం ఉష్ణోగ్రత గుణకం 1.70 × 10^-4° C^-1గా ఇచ్చారు.
సాధన:
R₂₇ = 100 Ω, R₁ = 117 Ω, t = ?
α = 1.70 × 10^-4/°C.

ప్రశ్న 6.
15m పొడవు, 6.0 × 10^-7m² ఏకరీతి మధ్యచ్ఛేద వైశాల్యం గల తీగ ద్వారా ఉపేక్షించదగినంత స్వల్పంగా విద్యుత్ను పంపారు. ఆ తీగ నిరోధం 5.0 Ω గా కొలవడమైనది. ఆ ప్రయోగం జరుగుతున్న ఉష్ణోగ్రత వద్ద ఆ పదార్థ నిరోధకత ఎంత?
సాధన:
l = 15 m, A = 6.0 × 10^-7 m², R = 5.0 Ω, ρ = ?

ప్రశ్న 7.
ఒక వెండి తీగ 27.5°C వద్ద 2.1 Ω నిరోధాన్ని, 100°C వద్ద 2.7 Ω నిరోధాన్ని కలిగి ఉంది. వెండి ఉష్ణోగ్రత నిరోధకత గుణకాన్ని కనుక్కోండి.
సాధన:
R_27.5 = 2.1 Ω, R₁₀₀ = 2.7 2; α = ?

ప్రశ్న 8.
నిక్రోమ్ చేసిన ఒక వేడెక్కే తీగను 230 V సరఫరాకు కలిపినప్పుడు అది తొలుత 3.2 A విద్యుత్ ప్రవాహం తీసుకుంటుంది. కొన్ని సెకన్ల తరువాత ఆ ప్రవాహం 2.8 A నిలకడ విలువకు చేరింది. గది ఉష్ణోగ్రత 27.0°C అయితే, వేడెక్కే తీగ నిలకడ ఉష్ణోగ్రత ఎంత ? దీనిలో తీసుకున్న ఉష్ణోగ్రతా అవధిపై సరాసరిన తీసుకొన్న నిక్రోమ్ తీగ ఉష్ణోగ్రతా నిరోధ గుణకం 1.70 × 10^-4 °C^-1.
సాధన:

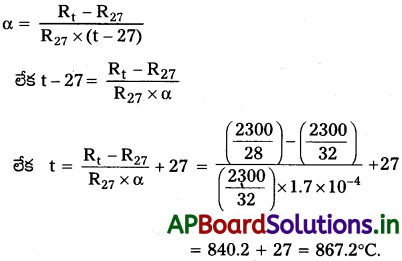
ప్రశ్న 9.
పటంలో చూపిన జాలం ప్రతి నిరోధకంలో విద్యుత్ ప్రవాహాన్ని కనుక్కోండి.

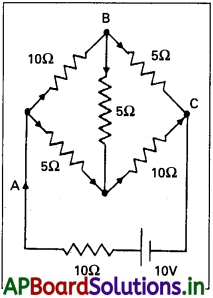
సాధన:
వలయం వేర్వేరు భుజాల ద్వారా పోవు విద్యుత్ ప్రవాహాలు పటంలో చూపబడినవి.
కిర్కాఫ్స్ రెండవ నియమం ప్రకారం,
EABCE సంవృత వలయంలో
-10 + 10 (i₁ + i₂) + 10i₁ 5(i₁ -i₃)=0
లేక 10 = 25i₁ + 10i₂ – 5i₃
లేక 2 = 5i₁ + 2i₂ – i₃ → (i)

ABDA సంవృత వలయంలో,
10i₁ + 5i₃ – 5i₂ = 0
లేక 2i₁ + i₃ – i₂ = 0
లేక i₂ = 2i₁ + i₃ → (ii)

BCDB సంవృత వలయంలో,
5(i₁ – i₃) – 10(i₂ + i₃) – 5i₃ = 0
లేక 5i₁ – 10i₂ – 20i₃ = 0
i₁ = 2i₂ + 4i₃ → (iii)
(ii) మరియు (iii) ల నుండి
i₁ = 2 (2i₁ + i₃) + 4i₃ = 4i₁ + 6i₃
లేక 3i₁ = −6i₃
లేక i₁ = -2i₃ → (iv)
ఈ విలువను (ii) లో వ్రాయగా,
i₂ = 2(−2i₃) + i₃ = – 3i₃ → (v)
ఈ విలువను (i) లో వ్రాయగా,
2 = 5(−2i₃) + 2(-3i₃) -i₃ లేక 2 = -17i₃
లేక i₃ = -2/17A
(iv) నుండి; i₁ = -2 (-2/17) = 4/17A
(v) నుండి; i₂ = -3(−2/17) = (6/17) A
∴ i₁ + i₂ = (4/17) + (6/17) = (10/17)A
i₁ – i₃ = 4/17 – (−2/17) = (6/17)A
i₂ + i₃ = (6/17) + (-2/17) = 4/17A.

ప్రశ్న 10.
a) మీటర్ బ్రిడ్జిలో Y నిరోధకం 12.5 Q అయినప్పుడు A కొన నుంచి 39.5 cm దూరంలో సంతులన బిందువును గుర్తించారు. X నిరోధాన్ని కనుక్కోండి. వీటన్ బ్రిడ్జి, మీటర్ బ్రిడ్జిలలోని నిరోధకాలను కలపడానికి మధ్యలో మందంగా గల రాగి పట్టీలను ఎందుకు ఉపయోగిస్తారు?

సాధన:

మందమైన రాగి పట్టీలను ఉపయోగించి, కల్పిత నిరోధంను తగ్గిస్తారు.

b) ఒకవేళ X, Y లను తారుమారుచేస్తే బ్రిడ్జి సంతులన బిందువును నిర్ధారించండి.
సాధన:
X మరియు Y లను పరస్పరము మార్చితే, 1, మరియు 1, (పొడవులు) కూడా మారును.
కావున l = 100 – 39.5′ = 60.5cm.

c) సంతులన బిందువు వద్ద గాల్వనామీటర్, ఘటాలను తారుమారుచేస్తే ఏమవుతుంది ? గాల్వనామీటర్ ఏదైనా విద్యుత్ ప్రవాహాన్ని చూపుతుందా ?
సాధన:
గాల్వనా మీటర్ విద్యుత్ ప్రవాహంను చూపదు.

ప్రశ్న 11.
8.0 Vemf, 0.5 Ω అంతర్నిరోధం గల ఒక సంచాయక ఘటమాలను 15.5Ω శ్రేణిలో గల నిరోధకం ఉపయోగించి 120 V dc సరఫరాకు కలిపి ఆవేశితం చేశారు. ఆవేశం చెందేటప్పుడు బ్యాటరీ టెర్మినల్ వోల్టేజి ఎంత ? ఆవేశం చెందించే వలయంలో శ్రేణిలో గల నిరోధకం ఆవశ్యకత ఏమిటి?
సాధన:
ఘటం వి.చా. బి. = 8.0 V
d.c. సప్లై వోల్టేజి = 120 V
ఘటం అంతర్నిరోధం, r = 0.5 Ω
బాహ్య నిరోధం, R = 15.5Ω
వి.చా.బ. 8V గల ఘటంను 120 V, d.c సప్లైతో ఆవేశపరిస్తే, వలయం ఫలిత వి.చా.బి.
E = 120 – 8 = 112 V
వలయం మొత్తం నిరోధం = R + r = 15.5+ 0.5. = 16.0Ω
∴ వలయంలో విద్యుత్, I = \(\frac{E}{R+r}=\frac{112}{16}\) = 7.0A
∴ R వెంట వోల్టేజి = IR = 7.0 × 15.5 = 108.5 V

వలయంలో d.c. సప్లై వోల్టేజి, R వెంట వోల్టేజి మరియు ఘటం అంత్య వోల్టేజిల మొత్తమునకు సమానం.
∴ 120 = 108.5 V లేక V = 120 – 108.5 = 11.5V

శ్రేణి నిరోధం, బాహ్య d.c జనక సప్లై నుండి తీసుకునే విద్యుత్ను లిమిట్ చేస్తుంది. నిరోధం లేకపోతే విద్యుత్ ఎక్కువ ప్రమాద స్థాయిలో ఉండును.

ప్రశ్న 12.
పొటెన్షియోమీటర్ అమరికలో 1.25 Vemf గల ఘటం సంతులన బిందువును 35.0 cm వద్ద ఇచ్చింది. ఈ ఘటాన్ని మార్చి దాని స్థానంలో మరొక ఘటాన్ని ఉంచినప్పుడు కొత్త సంతులన బిందువు 63.0 cm కి జరిగింది. రెండవ ఘటం em ఎంత? [AP. Mar.’15]
సాధన:

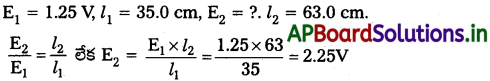
ప్రశ్న 13.
సాధించిన సమస్యల్లో 1వ ప్రశ్నలో అంచనావేసినట్లు ఒక రాగి వాహకంలోని స్వేచ్ఛా ఎలక్ట్రాన్ల సంఖ్య సాంద్రత 8.5 × 10²⁸ m^-3, 3.0 m పొడవు గల తీగ ఒక కొన నుంచి మరొక కొనకు డ్రిఫ్ట్ చెందటానికి ఎలక్ట్రాన్లకు ఎంత కాలం పడుతుంది ? తీగ మధ్యచ్ఛేద వైశాల్యం 2.0 × 10^-6 m², దాని గుండా 3.0 A విద్యుత్ ప్రవహిస్తుంది.
సాధన:
n = 8.5 × 10²⁸ m^-3; l = 3.0 m;
A = 2.0 × 10^-6 m²; I = 3.0 A, t = ?

అదనపు అభ్యాసాలు Additional Exercises

ప్రశ్న 14.
భూ ఉపరితలం 10° Cm రుణాత్మక ఉపరితల ఆవేశ సాంద్రతను కలిగి ఉంది. అత్యధిక ఎత్తులో గల వాతావరణ పై పొరకు, ఉపరితలానికి మధ్యగల 400 kV ప్రొటెన్షియల్ భేదం ఫలితంగా (తక్కువ ఎత్తులో గల వాతావరణం స్వల్ప వాహకత్వం వల్ల) గోళం (భూమి) అంతటా కేవలం 1800 A విద్యుత్ ప్రవాహం ఏర్పడుతుంది. ఒకవేళ అక్కడ వాతావరణ విద్యుత్ క్షేత్రాన్ని కొనసాగించే క్రియావిధానం లేకుంటే, భూఉపరితలాన్ని తటస్థం చేయడానికి (సుమారుగా) ఎంతకాలం అవసరం? (ఆచరణలో ఇలా ఎప్పటికీ జరుగదు. ఎందుకంటే (భూగోళంపై వివిధ ప్రదేశాల్లో సంభవించే మెరుపులు, తరచూ సంభవించే ఉరుములూ, మెరుపులతో కూడిన వర్షాల వల్ల విద్యుదావేశాలు తిరిగి నింపే క్రియావిధానం అక్కడ ఉంటుంది). (భూ వ్యాసార్థం = 6.37 × 10⁶m).
సాధన:
6.37 × 10⁶ m; σ = 10^-9cm^-2 ; I = 1800 A
గ్లోబ్ వైశాల్యం A = 4πr² = 4 × 3.14 × (6.37 × 10⁶)² = 509.64 × 10¹² m²
ఆవేశము, Q = σ × A = 10^-9 × 509.64 × 10¹²
= 509.64 × 10³ C
∴ t = \(\frac{Q}{I}=\frac{509.64 \times 10^3}{1800}\) = 283.1 s

ప్రశ్న 15.
a) ఒక్కొక్కటి 2.0 Vemf, 0.015 Q అంతర్నిరోధం గల ఆరు లేడ్ ఆసిడ్ రకం గౌణ ఘటాలను 8.5 Ω నిరోధానికి విద్యుత్ సరఫరా చేయడానికి శ్రేణిలో కలిపారు. విద్యుత్ సరఫరా నుంచి అది తీసుకునే విద్యుత్ ప్రవాహం, దాని టెర్మినల్ వోల్టేజీ ఎంత?
సాధన:

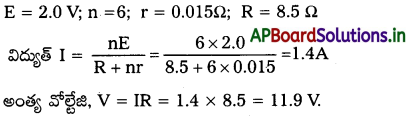
b) చాలాకాలం ఉపయోగించిన తరువాత ఒక గౌణ ఘటం 1.9 Vemf, 380 Ω అత్యధిక అంతర్నిరోధాన్ని కలిగి ఉంది. ఆ ఘటం నుంచి పొందగలిగే గరిష్ఠ విద్యుత్ ప్రవాహం ఎంత? ఒక కారు మోటారును ఈ ఘటం గుండా నడపగలుగుతుందా (ఆన్ చేయగలుగుతుందా)?
సాధన:
E = 1.9 V; r = 380 2
I_{గరిష్ఠ} = \(\frac{E}{r}=\frac{1.9}{380}\) = 0.005A
కొద్ది సెకనులు మోటారు స్టార్ట్ చేయుటకు కావలసిన విద్యుత్ 100 A. కావున పైన వచ్చిన విద్యుత్ విలువతో కారును స్టార్ట్ చేయలేము.

ప్రశ్న 16.
సమాన పొడవు గల అల్యూమినియం, రాగి తీగలు సమాన నిరోధాన్ని కలిగి ఉన్నాయి. ఆ రెండు తీగల్లో ఏది తేలికైనది ? చాలా ఎత్తు ‘మీద నుంచి పోయే విద్యుత్ సామర్థ్య తీగలుగా అల్యూమినియం తీగలను ఎందుకు ప్రాధాన్యం ఇస్తారో తెలపండి. (ρ_Al = 2.63 × 10^-8 Ωm, ρ^Cu 1.72 × 10^-8 Ωm, Al, Cu ల సాపేక్ష సాంద్రతలు వరుసగా 2.7, 8.9.)
సాధన:
అల్యూమినియం తీగకు, R₁ = R; l₁ = 1
సాపేక్ష సాంద్రత d₁ = 2.7.
రాగి తీగకు, R₂ = R, l₂ = l₁, d₂ = 8.9

A₁ మరియు A₂ లు అల్యూమినియం మరియు రాగి తీగల మధ్యచ్ఛేద వైశాల్యాలు అయితే

రాగి తీగ ద్రవ్యరాశి, అల్యూమినియం తీగ ద్రవ్యరాశికి 2.16 రెట్లు అని చూపును. ఒకే పొడవు అంతే నిరోధం గల అల్యూమినియం తీగ, రాగి తీగకన్నా తక్కువ ద్రవ్యరాశి కల్గి ఉండును. కావున పైన ఉండే పవర్ కేబుల్స్లో అల్యూమినియం తీగను వాడతారు. భారమైన కేబుల్స్, వాని బరువు వల్ల క్రిందికి సాగును.

ప్రశ్న 17.
మాంగనీస్ మిశ్రమ లోహంతో తయారైన నిరోధకంపై చేసిన కింది పరిశీలనల నుంచి మీరు ఏ నిర్ణయాన్ని తీసుకోగలుగుతారు?

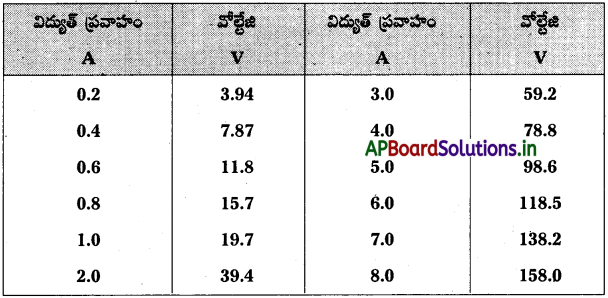
సాధన:
వేర్వేరు రీడింగుల, వోల్టేజి మరియు విద్యుత్ల నిష్పత్తి విలువలు సమానం. కావున ఓమ్స్ నియమము ఎక్కువ యదార్థతతో పాటించును. మాంగనీన్ విశిష్ట నిరోధం, ఉష్ణోగ్రతపై ఆధారపడదు.

ప్రశ్న 18.
కింది ప్రశ్నలకు సమాధానాలు ఇవ్వండి.
a) అసమరీతి మధ్యచ్ఛేద వైశాల్యం కలిగి ఉన్న లోహపు వాహకంలో నిలకడగా విద్యుత్ ప్రవహిస్తున్నది. కింది రాశులలో ఏవి వాహకం వెంబడి స్థిరంగా ఉంటాయి :
విద్యుత్ ప్రవాహం, విద్యుత్ ప్రవాహ సాంద్రత, విద్యుత్ క్షేత్రం, డ్రిఫ్ట్ వడి. సాధన. అసమ మధ్యచ్ఛేద వైశాల్య వాహకం ద్వారా పోవు విద్యుత్ మాత్రమే స్థిరం. మిగిలిన రాశులు వాహక మధ్యచ్ఛేద వైశాల్యంనకు విలోమానుపాతంలో ఉండును.

b) అన్ని వాహక మూలకాలకు ఓమ్ నియమం సార్వత్రికంగా అనువర్తనీయమా? ఒకవేళ కాకుంటే, ఓమ్ నియమాన్ని పాటించని మూలకాలకు ఉదాహరణలివ్వండి.
సాధన:
అఓమిక్ మూలకాలకు ఓమ్ నియమం వర్తించదు.
ఉదా : శూన్య నాళికలు, పాక్షిక వాహక డయోడ్లు, విద్యుద్విశ్లేష్య ద్రవాలు.

c) తక్కువ వోల్టేజి గల ఒక జనకం నుంచి అధిక విద్యుత్ ప్రవాహాలు అవసరమైనప్పుడు తప్పకుండా దాని అంతర్నిరోధం చాలా తక్కువగా ఉండాలి. ఎందుకు?
సాధన:

d) ఒక హైటెన్షన్ (high tension (HT)) సరఫరా 6 kV అనుకోండి, తప్పకుండా చాలా అధిక అంతర్నిరోధాన్ని కలిగి ఉండాలి. ఎందుకు?
సాధన:
HT సప్లయి చాలా ఎక్కువ అంతర్నిరోధం కలిగి ఉండును. అనుకోకుండా వలయం షార్ట్ అయితే, తీసుకునే విద్యుత్ సురక్షిత అవధిని దాటి వలయం పాడవటానికి కారణం అగును.

ప్రశ్న 19.
సరియైన ప్రత్యామ్నాయాన్ని ఎంచుకోండి :
a) సాధారణంగా మిశ్రమ లోహాల నిరోధకత వాటి అనుఘటక లోహాల నిరోధకతల కంటే (ఎక్కువ / తక్కువ).
b) మిశ్రమ లోహాల ఉష్ణోగ్రతా నిరోధ గుణకాలు శుద్ధలోహాల కంటే తక్కువ / ఎక్కువ).
c) ఉష్ణోగ్రత పెరుగుదలతో మాంగనీస్ మిశ్రమ లోహం నిరోధకత (ఉష్ణోగ్రతపై ఆధారపడదు / శీఘ్రంగా పెరుగుతుంది).
d) ఒక మాదిరి బంధకం (ఉదా : అంబర్ – సీమ గుగ్గిలం) నిరోధకత లోహ నిరోధకత కంటే (1022 1023) రెట్లు అధికం.
సాధన:
a) ఎక్కువ
b) తక్కువ
c) ఉష్ణోగ్రతపై ఆధారపడదు.
d) 1022

ప్రశ్న 20.
a) R నిరోధం గల నిరోధకాలను ఇవ్వడమైంది.
i) గరిష్ఠంగా, ii) కనిష్ఠంగా ప్రభావాత్మక నిరోధాన్ని పొందడానికి మీరు వాటిని ఏ విధంగా సంయోగం చేస్తారు ? గరిష్ఠ, కనిష్ట నిరోధం నిష్పత్తి ఎంత?
సాధన:
తుల్య నిరోధం గరిష్టం కావటానికి, n నిరోధాలను శ్రేణిలో కలపాలి.
గరిష్ట తుల్య నిరోధం, R_S = nR

తుల్య నిరోధం కనిష్టం కావటానికి, n నిరోధాలను సమాంతరంగా కలపాలి.
కనిష్ట తుల్య నిరోధం’, R_P = \(\frac{R}{n}\)
∴ \(\frac{\mathrm{R}_{\mathrm{S}}}{\mathrm{R}_{\mathrm{P}}}=\frac{\mathrm{nR}}{\frac{\mathrm{R}}{\mathrm{n}}}=\mathrm{n}^2\)

నిరోధాల సమాంతర సంయోగంలో తుల్య నిరోధం, విడివిడి నిరోధాల కన్నా తక్కువ మరియు నిరోధాల శ్రేణి సంయోగంలో తుల్య నిరోధం, విడివిడి నిరోధాల కన్నా ఎక్కువ.

b) 1Ω, 2Ω, 3Ω నిరోధాలు మీకివ్వడమైంది. కింద ఇచ్చిన తుల్య నిరోధాలను పొందడానికి వాటిని ఏ విధంగా సంయోగం చేస్తారు? i) (11/3) Ω (ii) (11/5) Ω, (iii) 6Ω, (iv) (6/11)Ω ?
సాధన:
సందర్భం (i) : 1Ω మరియు 2Ω ల సమాంతర సంయోగమును 3Ω లతో శ్రేణిలో కలిపినప్పుడు
1Ω మరియు 2Ω లను సమాంతరంగా కలచినప్పుడు, తుల్య నిరోధం

c) పటంలో చూపిన జాలాల (networks) తుల్య నిరోధాలను కనుక్కోండి.

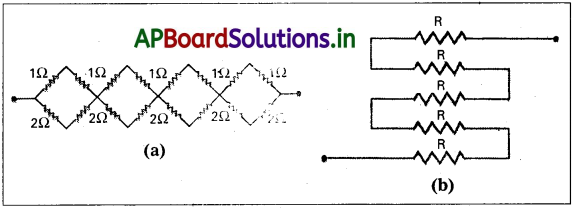
సాధన:
ఇచ్చిన వలయంను శ్రేణిలో 4 సమ భాగాల సంయోగము ప్రభావం 4 నిరోధాలు కలిగి ఉండును. వాటిలో ఒక్కొక్కటి 1Ω గల శ్రేణి నిరోధాలు 2 మరియు ఒక్కొక్కటి 2Ω గల సమాంతర నిరోధాలు 2.

ఒక్కొక్కటి 1Ω నిరోధం ఉన్న 2 నిరోధాల శ్రేణి. సన తుల్య నిరోధం= 1 + 1 = 2Ω.
ఒక్కొక్కటి 2Ω నిరోధం ఉన్న 2 నిరోధాల శ్రేణి సంధాన తుల్య నిరోధం = 2 + 2 = 4Ω
ఒక భాగంలో ఫలిత నిరోధం, \(\frac{1}{R_p}=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\) లేక R_p = \(\frac{3}{4}\)Ω
∴ 4 భాగాల మొత్తం నిరోధం R_p = \(\frac{3}{4}\) × 4 = \(\frac{16}{3}\)Ω = 5.33Ω
పటం (b)లో R నిరోధం ఉన్న 5 నిరోధాలు శ్రేణిలో కలిపారు. వాని తుల్య నిరోధం = 5R.

ప్రశ్న 21.
పటంలో చూపినట్లు అనంత జాలం, 0.5 Ω అంతర్నిరోధం గల 12V ల జనకం నుంచి పొందే విద్యుత్ ప్రవాహాన్ని కనుక్కోండి. ప్రతీ నిరోధకం 1 Ω నిరోధాన్ని కలిగి ఉంది.

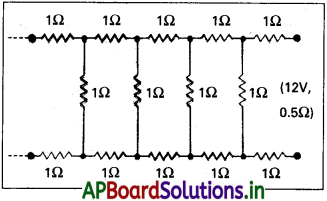
సాధన:
అనంతమైన నెట్వర్క్ తుల్య నిరోధం x.నెట్వర్క్ అనంతమైనది కావున టెర్మినల్స్ వెంట ఒక్కొక్కటి 1Ω విలువ గల మూడు నిరోధాల ప్రమాణంను కల్పితే నెట్వర్క్ మొత్తం నిరోధం మారదు. i. e., వలయం మిగిలిన నిరోధం x.
నెట్వర్క్ పటంలో చూపినట్లు ఉండును. మొత్తం నిరోధం x.

x మరియు 1Ω ల సమాంతర సంయోగము ఒక్కొక్కటి 1Ωగల 2 నిరోధాలతో శ్రేణితో కలపబడినవి.

ప్రశ్న 22.
AB నిరోధకం తీగ కొనల మధ్య పొటెన్షియల్ పాఠాన్ని కొనసాగిస్తున్న 2.0 V emf, 0.40 Ω అంతర్నిరోధం గల ఘటంతో గల పొటెన్షియో మీటర్ను పటం చూపుతుంది. 1.02 V స్థిర emf ను కొనసాగిస్తున్న ప్రామాణిక ఘటం (చాలా మిత విద్యుత్ ప్రవాహాలకు, కొన్ని mA విద్యుత్ ప్రవాహాల వరకు) 67.3 cm ల పొడవు వద్ద సంతులన బిందువును ఇస్తుంది. ప్రామాణిక ఘటం నుంచి కచ్చితంగా స్వల్ప విద్యుత్ ప్రవాహాలను పొందడానికి, దానితో శ్రేణిలో 600 kΩ అధిక నిరోధాన్ని కలిపారు.

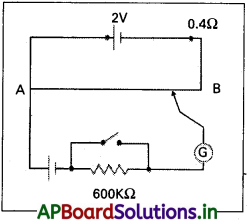
ఈ నిరోధాన్ని సంతులన బిందువుకు దగ్గరగా షార్ట్ (short) చేశారు. ఇప్పుడు ప్రామాణిక ఘటానికి బదులుగా తెలియని emf ε గల ఘటాన్ని అమర్చి, అదే విధంగా సంతులన పొడవును కనుక్కుంటే 82.3 cm పొడవు వద్ద సంతులన బిందువును ఇచ్చింది.
a) ε విలువ ఎంత?
సాధన:

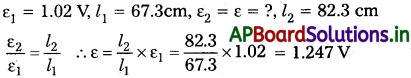
b) 600 kΩ నిరోధం అమర్చడానికి గల ఉద్దేశ్యమేమి?
సాధన:
600 kΩ హెచ్చు నిరోధం, గాల్వనామాపకం ద్వారా చాలా తక్కువ విద్యుత్ ప్రవాహంను అనుమతించును.

c) ఈ అధిక నిరోధం వల్ల సంతులన బిందువు ప్రభావితం అవుతుందా?
సాధన:
ఈ నిరోధం వలయంలో ఉండుట వల్ల తుల్యస్థానం మారదు.

d) చోదక ఘటం (driving cell) అంతర్నిరోధం వల్ల సంతులన బిందువు ప్రభావితం అవుతుందా?
సాధన:
విద్యుత్ ఘటం అంతర్నిరోధం వల్ల తుల్యస్థానం మారదు.

e) పొటెన్షియోమీటర్ చోదక ఘటం emf 2.0 V కు బదులుగా 1.0 V కలిగి ఉంటే పై పద్ధతి పనిచేస్తుందా?
సాధన:
కాదు. నడిచే ఘటం వి.చా. బ మరో ఘటం వి.చా. బ కన్నా తక్కువ అయితే పొటెన్షియోమీటర్ పద్ధతి పనికిరాదు. సంతులన బిందువును పొందలేము.

f) అత్యంత స్వలమైన emf లను, అంటే, కొన్ని mV ల వరకు (ఉష్ణయుగ్మం విలక్షణ emf లాంటివి) కనుక్కోవడానికి పై వలయం చక్కగా పనిచేస్తుందా? ఒకవేళ పనిచేయకపోతే, వలయాన్ని ఎలా మారుస్తారు?
సాధన:
స్వల్ప వి.చా. బ ను కొలుచుటకు వలయం పనికిరాదు. దీనికి కారణం సంతులన బిందువు A చివరకు దగ్గరగా ఉండును. వలయంను సరిచేయుటకు 2.0V ఘటంనకు శ్రేణిలో సరైన అధిక నిరోధంను ఉపయోగించాలి. ఇది పొటెన్షియో మీటర్ తీగ గుండా పోవు విద్యుత్ను తగ్గించును. కావున 1 cm తీగ పొటెన్షియల్ తేడా తగ్గును. కావున తక్కువ వి.చా. బను కనుగొనవచ్చును.

ప్రశ్న 23.
రెండు నిరోధాలను పోల్చడానికి పొటెన్షియోమీటర్ వలయాన్ని పటం సూచిస్తుంది. ప్రామాణిక నిరోధం R = 10.0 Ω తో సంతులన బిందువును 58.3 cm వద్ద కనుక్కొంటే, తెలియని నిరోధం X తో 68.5cm వద్ద సంతులన బిందువును కనుక్కొన్నారు. X విలువను కనుక్కోండి. ఒకవేళ emfe గల ఇచ్చిన ఘటంతో సంతులన బిందువును తెలుసుకోలేకపోతె, మీరు ఏం చేస్తారు?

సాధన:
l₁ = 58.3cm; l₂ = 68.5 cm; R = 10Ω; X = ?
పొటెన్షియోమీటర్ తీగలో విద్యుత్ I. R మరియు Xల వెంట పొటెన్షియల్లు E₁ మరియు E₂. కీని మూసి వలయంనకు R మరియు X లను కలిపితే అప్పుడు.

ఇచ్చిన ఘటం (వి. ఒ.బ) తో సంతులన బిందువు ఉండదు. దీని అర్థం R లేక X వెంట పొటెన్షియల్ డ్రాప్. పొటెన్షియోమీటర్ తీగ AB ట పొటెన్షియల్ డ్రాప్ కన్నా తక్కువ. R మరియు X లలో దేనికైనా సరైన నిరోధంను శ్రేణిలో ఉంచి లేక స్వల్ప వి. చా. బ ఉన్న ఘటంను ఉపయోగించి, R మరియు X గుండా పోవు విద్యుత్ తగ్గించి, వాని వెంట పొటెన్షియల్ డ్రాప్ తగ్గించి, సంతులన బిందువును పొందవచ్చును. మరియొక సాధ్యమగు మార్గము, వాడుతున్న ఘటం వోల్టేజి పెంచి, పొటెన్షియోమీటర్ తీగ వెంట పొటెన్షియల్ డ్రాప్ను పెంచవచ్చును.

ప్రశ్న 24.
పటం 1.5 Vఘటం అంతర్నిరోధం కనుక్కోవడానికి ఉపయోగించే 2.0V పొటెన్షియోమీటర్ను చూపిస్తుంది. వివృత వలయంలో ఘటం సంతులన బిందువు 76.3cm. ఘటం బాహ్య వలయంలో 9.5 Q నిరోధకాన్ని ఉపయోగించినపుడు, సంతులన బిందువు పొటెన్షియోమీటర్ తీగ పొడవు 64.8 cm వద్దకు జరిగింది. ఘటం అంతర్నిరోధం కనుక్కోండి.

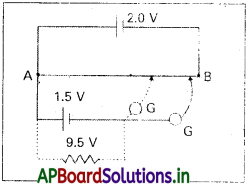
సాధన:

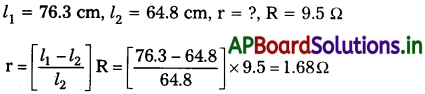
సాధించిన సమస్యలు Textual Examples

ప్రశ్న 1.
a) 1.0 × 10^-7 m² మధ్యచ్ఛేద వైశాల్యం, 1.5 A విద్యుత్ ప్రవాహాన్ని తీసుకొనిపోతున్న ఒక రాగితీగలోని వహన ఎలక్ట్రాన్ల సరాసరి డ్రిఫ్ట్ వడిని అంచనావేయండి. ప్రతి రాగి పరమాణువు సుమారుగా ఒక వహన ఎలక్ట్రాన్ న్ను ఇస్తుంది అని భావించండి. రాగి పరమాణు ద్రవ్యరాశి 63.5 u, సాంద్రత 9.0 × 10³ kg/m³
b) పై విధంగా పొందిన డ్రిఫ్ట ్వడిని కింద తెలియజేసిన వివిధ సందర్భాలలో గల వడితో పోల్చండి. i) సాధారణ ఉష్ణోగ్రతల వద్ద రాగి అణువుల ఉష్ట్రీయ వదులు (thermal speeds), ii) డ్రిఫ్ట్ చలనాన్ని కలుగచేసే వాహకం వెంబడి విద్యుత్ క్షేత్ర వ్యాపన వడి (speed of propagation).
సాధన:
a) వహన ఎలక్ట్రాన్ల డ్రిఫ్ట్వేగం దిశ విద్యుత్ క్షేత్ర దిశకు వ్యతిరేకంగా ఉంటుంది. అంటే ప్రొటెన్షియల్ పెరిగే దిశలో ఎలక్ట్రాన్లు క్రిఫ్ట్ అవుతాయి.

సమీకరణం I∆_t = + neA/υ_d/∆_t నుంచి డ్రిఫ్ట్ వడి υ_d = (I/neA)

ఇక్కడ e = 1.6 × 10^-19 C, A = 1.00 × 10^-7 m², I 1.5 A. ఒక ఘనపు మీటర్ లోని పరమాణువుల సంఖ్య వహన ఎలక్ట్రాన్ల సాంద్రత n కి సమానం. రాగి పరమాణువులో సంయోజక (వేలన్సీ) ఎలక్ట్రాన్ ఒకటి కాబట్టి, ప్రతి Cu పరమాణువుకు ఒక వహన ఎలక్ట్రానన్ను ఊహించడం సమంజసంగా ఉంటుంది. ఒక ఘనపు మీటర్ కాగి ద్రవ్యరాశి 9.0 × 10³ kg, 6.0 × 10²³ రాగి పరమాణువులు 63.5 g ద్రవ్యరాశిని కలిగి ఉంటాయి కాబట్టి

b) i) T ఉష్ణోగ్రత వద్ద, M ద్రవ్యరాశి గల రాగి పరమాణువుల ఉష్ట్రీయవడిని *[<(1/2) Mυ² > = (3/2) k_BT] నుంచి. పొందవచ్చు. ఇది విలక్షణంగా, \(\sqrt{\mathrm{k}_{\mathrm{B}} \mathrm{T} / \mathrm{M}}\) క్రమంలో ఉంటుంది. ఇక్కడ kB బోల్ట్స్ ఎన్ స్థిరాంకం. రాగి లోహానికి 300 K ఉష్ణోగ్రత వద్ద kg విలువ 2 × 10² m/s. ఈ విలువ వాహకంలోని రాగి పరమాణువుల అనియత కంపన వడులను తెలియజేస్తుంది. సాధారణ ఉష్ణోగ్రతల వద్ద విలక్షణ ఉష్ట్రీయ వడ్డీ కంటే ఎలక్ట్రాన్ల క్రిఫ్ట్ వడి 10^-5 రెట్లు తక్కువ అని గమనించండి.

ii) వాహకం వెంబడి ప్రయాణించే విద్యుత్ క్షేత్రం విద్యుదయస్కాంత తరంగాల వడి, అంటే 3.0 × 10⁸ ms^-1 ని కలిగి ఉంది. డ్రిఫ్ట్ వడిని విద్యుత్ క్షేత్రం వడితో పోల్చితే చాలా స్వల్పం, 10^-11 కారకంతో చిన్నది.

ప్రశ్న 2.
a) కొన్ని ఆంపియర్ల అవధిలో ఉండే విద్యుత్ ప్రవాహాలకు ఎలక్ట్రాన్ డ్రిఫ్ట్ వడి స్వల్పంగా mm s^-1 లో ఉంటుందని పై సమస్యలో అంచనావేయడమైంది. అయితే, ఇంచుమించు వలయాన్ని మూసిన వెంటనే విద్యుత్ ప్రవాహం ఏ విధంగా ఏర్పాటవుతుంది?
b) వాహకం లోపల గల విద్యుత్ క్షేత్రంలో ఎలక్ట్రాన్లు బలానికి గురికావడం వల్ల ఎలక్ట్రాన్ డ్రిఫ్ట్ ఉత్పత్తి అవుతుంది. కాని, బలం త్వరణాన్ని కలిగించాలి. అయితే ఎందుకు ఎలక్ట్రాన్లు నిలకడగా గల సరాసరి డ్రిఫ్ట్ వడిని పొందుతాయి?
c) ఎలక్ట్రాన్ ఆవేశం, డ్రిఫ్ట్ వడి చాలా స్వల్పం అయినప్పటికీ, వాహకంలో అధిక పరిమాణం గల ప్రవాహాలను మనం ఏ విధంగా పొందగలుగుతున్నాం?
d) ఒక లోహం లోపల ఎలక్ట్రాన్లు తక్కువ పొటెన్షియల్ నుంచి అధిక పొటెన్షియల్ వైపుకు డ్రిఫ్ట్కు చెందినప్పుడు, దీనర్థం ఆ లోహానికి చెందిన స్వేచ్ఛా ఎలక్ట్రాన్లు అన్నీ ఒకే దిశలో చలిస్తున్నాయా?
e) కింది రెండు సందర్భాల్లో వరుస అభిఘాతాల మధ్య (లోహం ధన అయాన్లతో) ఎలక్ట్రాన్ల పథం సరళరేఖలేనా?
i) విద్యుత్ క్షేత్రం లేనప్పుడు, ii) విద్యుత్ క్షేత్రం ఉన్నప్పుడు
సాధన:
a) వలయం అంతటా ప్రతి భాగంలో విద్యుత్ క్షేత్రం, ఇంచుమించు క్షణికంగా (కాంతివేగంతో) ఏర్పాటై, ప్రతి బిందువు వద్ద స్థానిక ఎలక్ట్రాన్ డ్రిఫ్ట్ ఏర్పడేట్లు చేస్తుంది. వాహకం ఒక కొన నుంచి మరొక కొనకు ఎలక్ట్రాన్లు ప్రయాణించే వరకు ప్రవాహ ఏర్పాటు వేచి ఉండాల్సిన అవసరం లేదు. అయితే, ప్రవాహం నిలకడ స్థితిని చేరడానికి మాత్రం అదీ స్వల్ప సమయాన్ని తీసుకొంటుంది.

b) ప్రతి స్వేచ్ఛా ఎలక్ట్రాన్ లోహం యొక్క ధన అయాన్తో అభిఘాతం చెందే వరకు త్వరణం చెంది దాని డ్రిఫ్ట్ వడిని పెంచుకొంటుంది. అభిఘాతం తరువాత తన డ్రిఫ్ట్ వడిని కోల్పోతుంది. కాని త్వరణం చెందడం ఆరంభం అవుతుంది. డ్రిఫ్ట్ వడి పెరుగుతుంది. తిరిగి అభిఘాతానికి లోనవుతుంది. ఇదే క్రమం జరుగుతూ ఉంటుంది. కాబట్టి సరాసరిగా, ఎలక్ట్రాన్లు డ్రిఫ్ట్ వడిని మాత్రమే పొందుతాయి.

c) ఎందుకంటే, ఎలక్ట్రాన్ సాంద్రత సంఖ్య చాలా పెద్దది ~ 10²⁹ m^-3.

d) అర్థరహితం. ఎలక్ట్రాన్ల అధిక అనియత వేగాలతో డ్రిఫ్ట్వేగం అధ్యారోపితం అవుతుంది.

e) విద్యుత్ కేత్రం లేనప్పుడు, పథాలు సరళరేఖలు, విద్యుత్ క్షేత్రం ఉన్నప్పుడు పథాలు సాధారణంగా వక్రాలు.

ప్రశ్న 3.
ఒక విద్యుత్ టోస్టర్ (toaster) లో వేడిచేయడానికి నిక్రోమ్ తీగని (heating element) ఉపయోగించుకొంది. గది ఉష్ణోగ్రత (27.0 °C) వద్ద దాని గుండా ఉపేక్షించదగిన స్వల్ప విద్యుత్ ప్రవహించినప్పుడు దాని నిరోధాన్ని 75.3 Ωగా కనుక్కొన్నారు. ఆ టోస్టర్ను 230 V ప్రధాన సరఫరాకి కలిపినప్పుడు విద్యుత్ ప్రవాహం స్థిరత్వం ఏర్పరచుకొని, కొన్ని సెకన్ల తరువాత 2.68 A నిలకడగా గల విలువకు చేరింది. నిక్రోమ్ తీగ నిలకడ ఉష్ణోగ్రత ఎంత ? పరిగణనలోకి తీసుకొన్న ఉష్ణోగ్రత అవధిపై సరాసరి ఉష్ణోగ్రత నిరోధ గుణకం విలువ 1:70 × 10^-4 °C^-1,
సాధన:
తీగ (heating element) ద్వారా ప్రవహించే విద్యుత్ ప్రవాహం చాలా స్వల్పంగా ఉన్నప్పుడు, ఉష్ణ ఫలితాలను ఉపేక్షించవచ్చు. దాని ఉష్ణోగ్రత T₁ గది ఉష్ణోగ్రత అంతం అవుతుంది. టోస్టర్ను సరఫరాకు కలిపినప్పుడు, తొలి ప్రవాహం, నిలకడ విలువ 2.68 A కంటే కొద్దిగా ఎక్కువగా ఉంటుంది. కాని విద్యుత్ ప్రవాహం వల్ల ఉష్ణ ఫలితం ఏర్పడి ఉష్ణోగ్రత పెరుగుతుంది. దీనితో నిరోధం పెరిగి విద్యుత్ ప్రవాహం కొద్దిగా తగ్గుతుంది. ఇంకా ఉష్ణోగ్రత పెరగకుంటే, కొద్ది సెకన్లలోనే నిలకడ స్థితికి చేరుతుంది. తీగ నిరోధం, తీసుకొన్న విద్యుత్ ప్రవాహం రెండూ నిలకడ విలువలను పొందుతాయి. నిలకడ ఉష్ణోగ్రత T₂ వద్ద, నిరోధం R₂ అనుకొంటే,

అందువల్ల, వేడెక్కే తీగ నిలకడ ఉష్ణోగ్రత (విద్యుత్ ప్రవాహం వల్ల కలిగే ఉష్ణ ఫలితం, పరిసరాలకు అయ్యే ఉష్ణ నష్టానికి సమానం అయినప్పుడు) విలువ 847 °C.

ప్రశ్న 4.
ఒక ప్లాటినం నిరోధపు థర్మామీటర్ లోని ప్లాటినం తీగ నిరోధం మంచు (ice point) బిందువు వద్ద 5 Ω, నీటి ఆవిరి (steam point) బిందువు వద్ద 5.39 Ω. ఈ థర్మామీటర్ను ఒక ఉష్ణతాపకంలోకి ప్రవేశపెట్టినప్పుడు ప్లాటినం తీగ నిరోధం 5.795 Ω. తాపకం ఉష్ణోగ్రతను లెక్కించండి.
సాధన:
R₀ = 5 Ω, R₁₀₀ = 5.23 Ω, R_t = 5.795 Ω

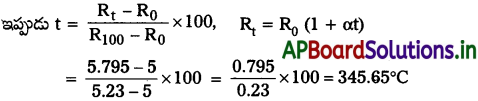
ప్రశ్న 5.
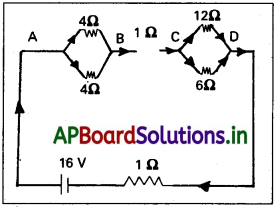
నిరోధకాల ఒక జాలం, (network) ను 10 అంతర్నిరోధం గల 16 V బ్యాటరీకి పటంలో చూపినట్లు సంధానం చేశారు :
a) జాలం తుల్య నిరోధాన్ని గణించండి.
b) ప్రతీ నిరోధకంలో విద్యుత్ ప్రవాహాన్ని రాబట్టండి.
c) V_AB V_BC, V_CD వోల్టేజి పాతాలను పొందండి.

సాధన:
a) ఈ జాలం నిరోధకాల శ్రేణి, సమాంతర సంయోగం. మొదటి రెండు 4 Ω నిరోధకాలు సమాంతరంగా కలవు. వీటి ఫలితం = [(4 × 4)/ (4 + 4)] Ω = 2 Ω నిరోధానికి తుల్యమవుతుంది.

అదే విధంగా, 122, 62 నిరోధకాలు సమాంతరంగా కలవు. వీటి ఫలితం = [(12×6) / (12 + 6)] Ω = 4Ω నిరోధానికి తుల్యమవుతుంది. జాలం తుల్య నిరోధం R ను పై రెండు నిరోధకాల (2Ω, 4Ω) ను 12 తో శ్రేణిని కలిపి రాబట్టవచ్చు.
R = 2Ω + 4Ω + 1Ω = 7Ω

b) వలయంలో మొత్తం విద్యుత్ ప్రవాహం అనుకొంటే,
I = \(=\frac{\varepsilon}{R+r}=\frac{16 V}{(7+1) \Omega}\)

A, B ల మధ్య నిరోధకాలను పరిగణించండి. ఆ రెండింటిలో 4 Ω నిరోధం గల ఒక దానిలో విద్యుత్ I₁ అనుకొంటే, రెండవ దానిలో విద్యుత్ I₂ అవుతుంది.
I₁ × 4 = I₁ × 4
అంటే, I₁ = I₂ మరో విధంగా చూస్తే రెండు భుజాల సౌష్టవం వల్ల కూడా ఇది స్పష్టం. కాని I₁ + I₂ = I = 2A. కాబట్టి, I₁ = I₂ = IA

ప్రతీ 4 Ω నిరోధకంలోని విద్యుత్ ప్రవాహం 1 A, B, C ల మధ్య గల 1 Ω నిరోధకంలోని విద్యుత్ ప్రవాహం 2 A అవుతుంది. ఇప్పుడు C, D ల మధ్య గల రెండు నిరోధకాలను తీసుకొంటే, 12 Ω నిరోధకంలో విద్యుత్ ప్రవాహం I₃, 6 Ω నిరోధకంలో I₄ అనుకోండి.
I₃ × 12 = I₄ × 6 i. e., I₄ = 2I₃
కానీ, I₃ + I₄ = I = 2A
అందువల్ల I₃ = (\(\frac{2}{3}\))A, I₄ = (\(\frac{4}{3}\))A
అంటే 12Ω నిరోధకంలో విద్యుత్ ప్రవాహం (2/3) A, అదే సమయంలో 6Ω నిరోధకంలో విద్యుత్ ప్రవాహం (4/3) A.

c) AB కొనల మధ్య వోల్టేజి పాతం, V_AB = I₁ × 4 = 1 A × 4Ω = 4 V.
ఈ విలువను A, B ల మధ్య గల మొత్తం విద్యుత్ ప్రవాహాన్ని, A, B ల మధ్య గల తుల్య నిరోధంతో గుణించి కూడా రాబట్టవచ్చు. అంటే,
V_AB = 2A × 2 Ω =4V
BC కొనల మధ్య వోల్టేజి పాతం,
V_BC = 2A × 1 Ω = 2V
CD కొనల మధ్య వోల్టేజి పాతం,
V_CD = 12 Ω × I₃ = 12Ω × (\(\frac{2}{3}\)) A = 8 V.

ఈ విలువను C, D ల మధ్యగల మొత్తం విద్యుత్ ప్రవాహాన్ని, C, D ల మధ్య తుల్య నిరోధంతో గుణించి రాబట్టవచ్చు. అంటే, V_CD = 2 A × 4 Ω = 8 V

AD కొనల మధ్య మొత్తం వోల్టేజి పాతం, 4 V+ 2 V + 8 V = 14 V అని గమనించండి. ఘటం కొనల మధ్య వోల్టేజి, (టెర్మినల్ వోల్టేజి) 14 V. అదే సమయంలో దాని emf 16 V. వోల్టేజిలో కలిగే నష్టం (= 2 V), ఈ నష్టం ఘటం అంతర్నిరోధం 1Ω వల్ల జరుగుతుంది [2 A × 1Ω = 2 V).

ప్రశ్న 6.
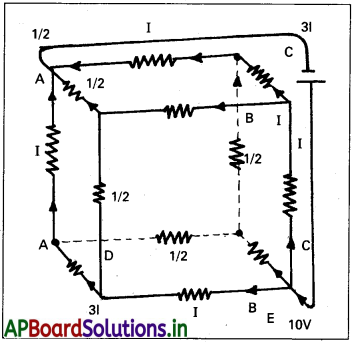
ఒక్కొక్కటి 1Ω నిరోధం గల 12 నిరోధకాలను కలిగి ఉన్న ఘనాకార జాలం కర్ణాల ఎదురెదురు కొనల మధ్య ఉపేక్షించదగిన అంతర్నిరోధం ‘గల 10 V బ్యాటరీని సంధానం చేశారు. జాలం తుల్య నిరోధాన్ని, ఘనం ప్రతీ అంచు ద్వారా ప్రవహించే విద్యుత్ ప్రవాహాన్ని కనుక్కోండి.

సాధన:
ఈ జాలాన్ని నిరోధకాల సరళశ్రేణి, సమాంతర సంయోగాలకు తగినట్లుగా రూపాంతరం చెందించలేం. అయితే, ఇచ్చిన లెక్కలో స్పష్టమైన సౌష్టవం ఉంది కాబట్టి దానిని ఉపయోగించుకొని జాలం తుల్య నిరోధాన్ని పొందవచ్చు.

AA’, AD, AB పథాలను స్పష్టంగా, సౌష్టవంగా ఉండేటట్లు జాలంలో ఉంచారు. కాబట్టి, ప్రతీ దానిలోని విద్యుత్ ప్రవాహం I సమానంగా ఉండాలి. ఇంకా A’, B, D కొనల వద్ద లోపలికి ప్రవేశించే విద్యుత్ ప్రవాహం I బయటికి పోయే రెండు శాఖల్లోకి తప్పకుండా రెండు సమాన భాగాలుగా విడిపోవాలి.

ఈ విధంగా లెక్కలోని సౌష్టవం, కిర్కాఫ్ మొదటి నియమాన్ని ఉపయోగించి ఘనం 12 అంచులలోని విద్యుత్ ప్రవాహాన్ని I పదాలలో సులభంగా రాయవచ్చు. తరువాత ABCCEA సంవృత లూపు తీసుకొని కిర్కాఫ్ రెండవ నియమాన్ని అనువర్తించండి :

-IR – (1/2) IR – IR + ε = 0

ఇక్కడ R ప్రతీ అంచు నిరోధం, ε ఘటం emf. అందువల్ల, ε = \(\frac{5}{2}\)IR
జాలం తుల్య నిరోధం R_eq అనుకొంటే, R_eq = \(\frac{\varepsilon}{3I}=\frac{5}{6}\)R
R = 1Ω కు R_eq = (5/6) Ω, ε = 10V అయితే జాలంలోని మొత్తం విద్యుత్ ప్రవాహం (=3I)
3I = 10V/(5/6) Ω = 12 A, అంటే, I = 4 A

ప్రశ్న 7.
పటంలో చూపిన జాలంలో ప్రతీ శాఖలోని విద్యుత్ ప్రవాహాన్ని కనుక్కోండి.

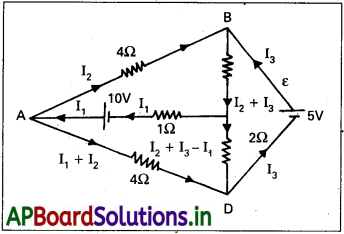
సాధన:
జాలం ప్రతీ శాఖ తెలియని విద్యుత్ ప్రవాహంతో నిర్దేశితమై ఉంది. వీటిని కిర్కాఫ్ నియమాలను ఉపయోగించి కనుక్కోవలసి ఉంది. మొదట తెలియని వాటి సంఖ్యను తగ్గించడానికి, ప్రతీ శాఖలో తెలియని విద్యుత్ ప్రవాహాన్ని నిర్దేశించడానికి ప్రతీ సంధి వద్ద కిర్కాఫ్ మొదటి నియమాన్ని ఉపయోగించాలి. అప్పుడు మనకు I₁, I₂, I₃ అనే మూడు తెలియనివి – ఉన్నాయి. వీటిని మూడు వివిధ సంవృత లూప్లు కిర్కాఫ్ రెండవ నియమాన్ని అనువర్తించి కనుక్కోవచ్చు. ADCA సంవృత లూప్కు కిర్కాఫ్ రెండవ నియమాన్ని ఉపయోగిస్తే,
10 – 4(I₁ – I₂) + 2 (I₂ + I₃ – I₁) – I₁ = 0
అంటే, 7I₁ – 6I₂ – 2I₃ = 10 → (1)

ABCA సంవృత వలయానికి ఉపయోగిస్తే,
10 -4I₂ – 2 (I₂ + I₃) – I₁ = 0
అంటే, I₁ + 6I₂ + 2I₃ = 10 → (2)

BCDEB సంవృత వలయానికి ఉపయోగిస్తే,
5 – 2 (I₂ + I₃) – 2 (I₂ + I₃ – I₁) = 0
అంటే, 2I₁ – 4I₂ – 4I₃ = -5. → (3)

సమీకరణాలు (1, 2, 3) మూడు తెలియని విలువలు కలిగి ఉన్న సమకాలిక సమీకరణాలు. వీటిని సాధారణ. పద్ధతుల్లో సాధించినట్లయితే, కింది విలువలు వస్తాయి.

మిగతా సంవృత లూప్లకు కిర్కాఫ్ రెండవ నియమాన్ని అనువర్తించినట్లయితే, ఏ మాత్రం అదనపు స్వతంత్ర సమీకరణాన్ని సమకూర్చదని సులభంగా నిరూపితమైంది. అంటే, పై విద్యుత్ ప్రవాహ విలువలు జాలంలోని ప్రతీ సంవృత లూప్కు కిర్కా రెండవ నియమాన్ని సంతృప్తిపరుస్తాయి. ఉదాహరణకు, సంవృత లూప్ BADEB కి మొత్తం వోల్టేజి పాతం

కిరాఫ్ రెండవ నియమం ప్రకారం అవసరమైనట్లు, ఇది శూన్యానికి సమానం.

ప్రశ్న 8.
వీటన్ బ్రిడ్జి నాలుగు భుజాలు ఈ క్రింది విధంగా నిరోధాలను కలిగి ఉన్నాయి.

AB = 100Ω, BC = 10Ω, CD = 5Ω, DA= 60Ω BD కొనల మధ్య 15Ω నిరోధం గల గాల్వనామీటర్ను కలిపారు. AC ల మధ్య 10 V పొటెన్షియల్ భేదం కొనసాగించినప్పుడు, గాల్వనామీటర్ ద్వారా విద్యుత్ . ప్రవాహాన్ని కనుక్కోండి.
సాధన:
BADB వల (mesh) ను పరిగణనలోకి తీసుకొంటే,
100I₁ + 15I_g – 60I₂ = 0 లేదా 20I₁ + 3I_g – 12I₂ = 0 → (1)

BCDB వలను పరిగణనలోకి తీసుకొంటే,
10(I₁ – I_g) – 15I_g – 5(I₂ + I_g) = 0
10I₁ – 30I_g – 5I₂ = 0
2I₁ – 6I_g – I₂ = 0 → (2)

ADCEA వలను పరిగణనలోకి తీసుకొంటే,
60I₂ + 5(I₂ + I_g) = 10
65I₂ + 5I_g = 10
13I₂ + I_g = 2
సమీకరణం (2) ని 10 తో గుణిస్తే,
20I₁ + 60I_g – 10I₂ = 0
సమీకరణాలు (4) మరియు (1) ల నుంచి
63I_g – 2I₂ = 0
I₂ = 31.5I_g

పై I₂ విలువను సమీకరణం (3) లో ప్రతిక్షేపిస్తే,
13(31.5I_g) + I_g = 2
410.5 I_g = 2
I_g = 4.87 mA.

ప్రశ్న 9.
మీటరు బ్రిడ్జిలో A నుంచి 36.7 cm ల దూరం వద్ద శూన్య బిందువును కనుక్కొన్నారు. ఇప్పుడు 12Ω నిరోధాన్ని S కి సమాంతరంగా కలిపితే, శూన్య బిందువు 51.9 cm వద్ద కలుగుతుంది. R, S విలువలను కనుక్కోండి.

సాధన:
మొదటి సంతులన బిందువు నుంచి కింది విధంగా వస్తుంది.

సమీకరణం (1) నుంచి R/S విలువ పై సమీకరణంలో ప్రతిక్షేపిస్తే,

దీని నుంచి S = 13.5 Ω వస్తుంది. పై R/S విలువను ఉపయోగిస్తే, మనకు R = 6.86Ω వస్తుంది.

ప్రశ్న 10.
RΩ ల ఒక నిరోధం పొటెన్షియోమీటర్ నుంచి విద్యుత్ ప్రవాహాన్ని తీసుకుంటుంది. పొటెన్షియోమీటర్ కలిగి ఉండే మొత్తం నిరోధం R₀ Ω. పొటెన్షియోమీటరు సరఫరా అయిన వోల్టేజి V. జాకీ (తీగపై జారుతూ తీగతో స్పర్శలో ఉండేది) పొటెన్షియోమీటర్ మధ్యలో ఉన్నప్పుడు, R కొనల మధ్య ఉండే వోల్టేజికి సమీకరణాన్ని ఉత్పాదించండి.

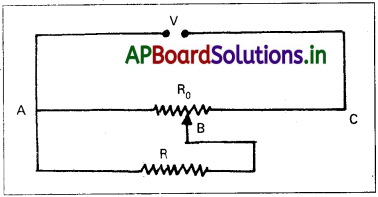
సాధన:
జాకీ పొటెన్షియోమీటర్ మధ్యలో ఉన్నప్పుడు మాత్రమే A, B బిందువుల మధ్య నిరోధం మొత్తం నిరోధంలో సగం (R₀/2) ఉంటుంది. అందువల్ల A, B ల మధ్య గల మొత్తం నిరోధం R₁ అనుకుంటే, దీనిని కింది సమాసంగా ఇవ్వచ్చు.

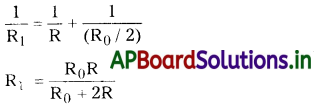
A, C. మధ్య గల మొత్తం నిరోధం A, B, B, C ల మధ్య గల నిరోధాల మొత్తానికి సమానం. అంటే, R₁ + R₀ /2
∴ పొటెన్షియోమీటర్ ద్వారా ప్రవహించే విద్యుత్,