SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు Ex 1.1 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు Exercise 1.1
ప్రశ్న 1.
కింది ఉదాహరణలలో ఉన్న ధర్మాలను గుర్తించి వ్రాయండి.
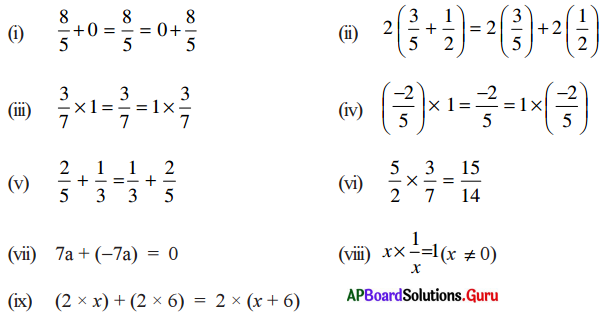
సాధన.

ప్రశ్న 2.
కింది వాటికి సంకలన మరియు గుణకార విలోమాలు వ్రాయండి.
(i) \(\frac {-3}{5}\)
(ii) 1
(iii) 0
(iv) \(\frac {7}{9}\)
(v) -1
సాధన.
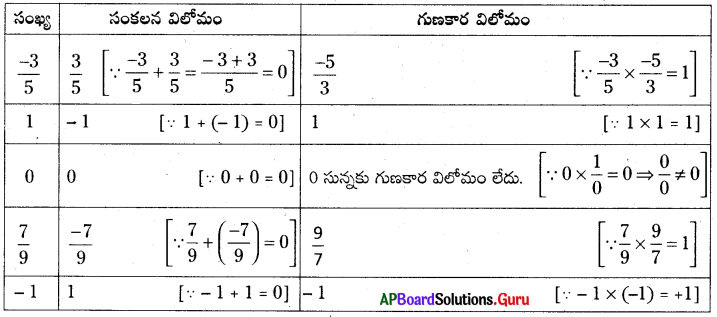
![]()
ప్రశ్న 3.
కింది ఖాళీలను పూరించండి.

సాధన.
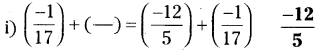

ప్రశ్న 4.
\(\frac {2}{11}\) ను \(\frac {-5}{14}\) యొక్క గుణకార విలోమంతో గుణించండి.
సాధన. \(\frac {-5}{14}\) యొక్క గుణకార విలోమం = 14
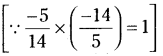
∴ \(\frac{2}{11} \times\left(\frac{-14}{5}\right)=\frac{-28}{55}\)
ప్రశ్న 5.
\(\frac{2}{5} \times\left[5 \times \frac{7}{6}\right]+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)\) యొక్క గణనలో ఏయే ధర్మాలను ఉపయోగిస్తాము ?
సాధన.
\(\frac{2}{5} \times\left[5 \times \frac{7}{6}\right]+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)\) యొక్క గణనలో
గుణకార సహచర ధర్మం
గుణకార విలోమం
గుణకార తత్సమాంశం
సంకలన సంవృతం అనే ధర్మాలను ఉపయోగిస్తాము.
![]()
ప్రశ్న 6.
కింది సమానత్వాన్ని సరిచూడండి.
\(\left(\frac{5}{4}+\frac{-1}{2}\right)+\frac{-3}{2}=\frac{5}{4}+\left(\frac{-1}{2}+\frac{-3}{2}\right)\)
సాధన.
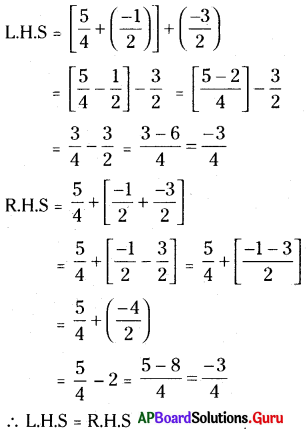
ప్రశ్న 7.
\(\frac{3}{5}+\frac{7}{3}+\left(\frac{-2}{5}\right)+\left(\frac{-2}{3}\right)\) విలువను పదాల అమరికను మార్చి సూక్ష్మీకరించండి.
సాధన.

ప్రశ్న 8.
కింది వాటిని వ్యవకలనం చేయండి.
(i) \(\frac {1}{3}\) నుండి \(\frac {3}{4}\)
(ii) 2 నుండి \(\frac {-32}{13}\)
(iii) \(\frac {-4}{7}\) నుండి -7
సాధన.
(i) \(\frac {1}{3}\) నుండి \(\frac {3}{4}\)
\(\frac{1}{3}-\frac{3}{4}=\frac{4-9}{12}=\frac{-5}{12}\)
(ii) 2 నుండి \(\frac {-32}{13}\)
2 – \(\frac {-32}{13}\)
= 2 + \(\frac {32}{13}\)
= \(\frac{26+32}{13}\)
= \(\frac {58}{13}\)
(iii) \(\frac {-4}{7}\) నుండి -7
\(\frac {-4}{7}\) – (-7)
= \(\frac {-4}{7}\) + 7
= \(\frac{-4+49}{7}\)
= \(\frac {45}{7}\)
![]()
ప్రశ్న 9.
\(\frac {-5}{8}\) కు ఎంత కలిపిన \(\frac {-3}{2}\) వచ్చును ?
సాధన.
\(\left(\frac{-5}{8}\right)+x=\left(\frac{-3}{2}\right)\)
⇒ x = \(-\frac{3}{2}+\frac{5}{8}=\frac{-3 \times 4+5}{8}\)
= \(\frac{-12+5}{8}\)
x= \(\frac {-7}{8}\)
= \(\frac {45}{7}\)
∴ \(\frac {-5}{8}\) నకు (\(\frac {-7}{8}\)) కలిపిన \(\frac {-3}{2}\) వచ్చును.
ప్రశ్న 10.
రెండు అకరణీయ సంఖ్యల మొత్తం 8. వాటిలో ఒక సంఖ్య \(\frac {-5}{6}\) అయితే రెండవ సంఖ్య ఎంత ?
సాధన.
రెండవ సంఖ్య = x అనుకొనుము.
x + (\(\frac {-5}{6}\)) = 8 ⇒ x = 8 + \(\frac {5}{6}\)
= \(\frac{48+5}{6}\)
x = \(\frac {53}{6}\)
ప్రశ్న 11.
వ్యవకలనం దృష్ట్యా అకరణీయ సంఖ్యలు సహచర ధర్మాన్ని పాటిస్తాయా ? ఒక ఉదాహరణతో వివరించండి.
సాధన.
\(\frac{1}{2}, \frac{3}{4}, \frac{-5}{4}\) ఏవైనా 3 అకరణీయ సంఖ్యలు.
వ్యవకలన సహచర ధర్మం
⇒ a – (b – c) = (a – b) – c ను పాటిస్తుందో లేదో చూద్దాం.
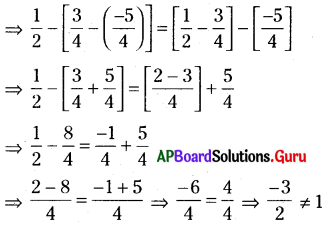
∴ L.H.S ≠ R.H.S
వ్యవకలనం దృష్ట్యా అకరణీయ సంఖ్యలు సహచర ధర్మాన్ని పాటించవు.
∴ a – (b – c) ≠ (a – b) – c
ప్రశ్న 12.
– (-x) = x ను కింది విలువలకు సరిచూడండి.
(i) x = \(\frac {2}{15}\)
(ii) x = \(\frac {-13}{17}\)
సాధన.
(i) x = \(\frac {2}{15}\)
⇒ -(-x) = -(\(\frac {-2}{15}\)) = \(\frac {2}{15}\) [∵ (-) × (-) = +]
(ii) x = \(\frac {-13}{17}\)
-(-x) = \(-\left[-\left(\frac{-13}{17}\right)\right]=-\left[\frac{13}{7}\right]=\frac{-13}{7}\) [∵ (-) × (+) = -]
∴ పై రెండు ఉదాహరణల నుండి ‘x’ విలువ ఏదైనప్పటికీ – (-x) = x అగును.
![]()
ప్రశ్న 13.
కింది వానికి జవాబులు వ్రాయండి.
i) సంకలన తత్సమాంశం కలిగి వుండని సమితి ఏది ?
సాధన.
సంకలన తత్సమాంశం (0) కలిగి ఉండని సమితి N.
సహసంఖ్యా సమితిలో “సున్న” (0) ఉండదు.
ii) గుణకార విలోమం లేని అకరణీయ సంఖ్య ఏది ?
సాధన.
గుణకార విలోమం లేని అకరణీయ సంఖ్య ‘0’.
[∵ \(\frac {1}{0}\) ను నిర్వచించలేము కనుక]
iii) ఋణ అకరణీయ సంఖ్య యొక్క గుణకార విలోమం ?
సాధన.
ఋణ అకరణీయ సంఖ్య యొక్క గుణకార విలోమం
ఒక ఋణ అకరణీయ సంఖ్య అవుతుంది.
∵ \(\frac{-2}{5} \times\left(\frac{-5}{2}\right)=1\)