AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions Ex 10.4

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions Ex 10.4 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions Exercise 10.4

Question 1.
Rice costing ₹480 is needed for 8 members for 20 days. What is the cost of rice required for 12 members for 15 days?
Solution:
Method – 1: Number of men and rice required to them are in inverse proportion.
Number of men ∝ \(\frac{1}{\text { No. of days }}\)

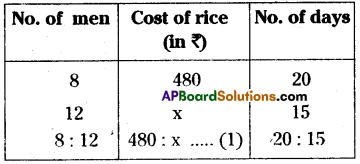
⇒ Compound ratio of 8:12 and 20: 15
= \(\frac{8}{12}=\frac{20}{15}\) = \(\frac{8}{9}\) …………….. (2)
From (1), (2)
480 : x = 8 : 9
⇒ \(\frac{480}{x}=\frac{8}{9}\)
⇒ x = \(\frac{480 \times 9}{8}\) = ₹540
∴ The cost of required rice is ₹ 540

Method – II :
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
M₁ = No. of men
D₁ = No .of days
W₁ = Cost of rice
∴ M₁ = 8
D₁ = 20
W₁ = ₹ 480
M₂ = 12
D₂ = 15
W₂ = ? (x)

⇒ x = 45 x 12 = ₹ 540
The cost of required rice = ₹ 540/-

Question 2.
10 men can lay a road 75 km. long in 5 days. In how many days can 15 men lay a road 45 km. long?
Solution:
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
∴ M₁ = 10
D₁ = 5
W₁ = 75
M₂ = 15
D₂ = ?
W₂ = 45

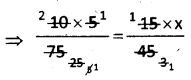
∴ x = 2
∴ No. of days are required = 2

Question 3.
24 men working at 8 hours per day can do a piece of work in 15 days. In how many days can 20 men working at 9 hours per day do the same work?
Solution:
M₁D₁H₁ = M₂D₂H₂
∴ M₁ = 24
D₁ = 15 days
H₁ = 8 hrs
M₂ = 20
D₂ = ?
H₂ = 9 hrs
⇒ 24 × 15 × 8 = 20 × x × 9

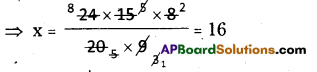
∴ No. of days are required = 16
[ ∵ No. of men and working hours are in inverse]

Question 4.
175 men can dig a canal 3150 m long in 36 days. How many men are required to dig a canal 3900 m. long in 24 days?
Solution:
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
M₁ = 175
D₁ = 36
W₁ = 3150
M₂ = ?
D₂ = 24
W₂ = 3900

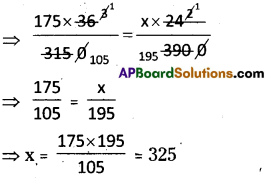
∴ No. of workers are required = 325

Question 5.
If 14 typists typing 6 hours a day can take 12 days to complete the manuscript of a book, then how many days will 4 typists, working 7 hours a day, can take to do the same job?
Solution:
M₁D₁H₁ = M₂D₂H₂
M₁ = 14
D₁ = 12 days
H₁ = 6
M₂ = 4
D₂ = ?
H₂ = 7
⇒ 14 × 12 × 6 = 4 × x × 7

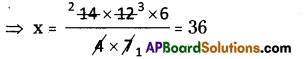
⇒ x = 36
∴ No. of days are required = 36
[ ∵ No of men and working hours are in inverse proportion]