SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.5 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.5
ప్రశ్న 1.
క్రింది సమీకరణాలను సాధించుము.
(i) \(\frac{n}{5}-\frac{5}{7}=\frac{2}{3}\)
సాధన.
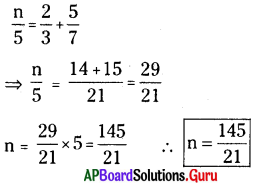
(ii) \(\frac{x}{3}-\frac{x}{4}=14\)
సాధన.
\(\frac{4 x-3 x}{12}\) = 14 ⇒ \(\frac{\mathrm{x}}{12}\) = 14
⇒ x = 12 × 14 = 168
∴ x = 168
(iii) \(\frac{z}{2}+\frac{z}{3}-\frac{z}{6}=8\)
సాధన.
\(\frac{3 z+2 z-z}{6}\) = 8
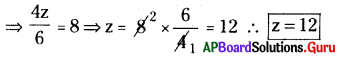
(iv) \(\frac{2 p}{3}-\frac{p}{5}=11 \frac{2}{3}\)
సాధన.

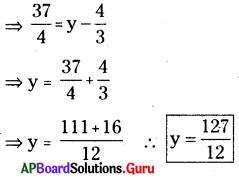
(v) \(9 \frac{1}{4}=y-1 \frac{1}{3}\)
సాధన.
![]()
(vi) \(\frac{x}{2}-\frac{4}{5}+\frac{x}{5}+\frac{3 x}{10}=\frac{1}{5}\)
సాధన.
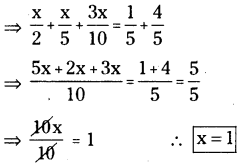
(vii) \(\frac{x}{2}-\frac{1}{4}=\frac{x}{3}+\frac{1}{2}\)
సాధన.

(viii) \(\frac{2 x-3}{3 x+2}=\frac{-2}{3}\)
సాధన.
⇒ 3(2x – 3) = – 2(3x + 2)
⇒ 6x – 9 = – 6x – 4
⇒ 6x + 6x = – 4 + 9
⇒ 12x = 5
∴ x = \(\frac {5}{12}\)
(ix) \(\frac{8 p-5}{7 p+1}=\frac{-2}{4}\)
సాధన.
\(\frac{8 p-5}{7 p+1}=\frac{-1}{2}\)
⇒ 2(8p – 5) = -(7p + 1)
⇒ 16p – 10 = – 7p – 1
⇒ 16p + 7p = – 1 + 10
⇒ 23p = 9
∴ p = \(\frac {9}{23}\)
(x) \(\frac{7 y+2}{5}=\frac{6 y-5}{11}\)
సాధన.
⇒ 11(7y + 2) = 5 (6y – 5)
⇒ 77y + 22 = 30y – 25
⇒ 77y – 30y = – 25 – 22
⇒ 47y = – 47 ⇒ y = \(\frac {-47}{47}\)
∴ y = -1
(xi) \(\frac{x+5}{6}-\frac{x+1}{9}=\frac{x+3}{4}\)
సాధన.
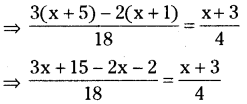
⇒ 4(x + 13) = 18 (x + 3)
⇒ 4x + 52 = 18x + 54
⇒ 4x – 18x = 54 – 52
⇒ – 14x = 2
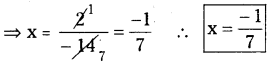
(xiii) \(\frac{3 t+1}{16}-\frac{2 t-3}{7}=\frac{t+3}{8}+\frac{3 t-1}{14}\)
సాధన.

– 11t – 38t = 34 – 55
= – 49t = – 21
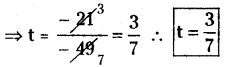
![]()
ప్రశ్న 2.
ఒక సంఖ్య యొక్క 3వ భాగము దాని 5వ భాగము కంటే 4 ఎక్కువ అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
x యొక్క 3వ భాగం = \(\frac{x}{3}\)
x యొక్క 5వ భాగం = \(\frac{x}{5}\)

ప్రశ్న 3.
రెండు ధనసంఖ్యల భేదం 36. ఒక దానిని రెండవ దానితో భాగించగా వచ్చే భాగఫలం 4 అయిన వానిని కనుగొనుము.
(సూచన : ఒక సంఖ్య ‘x’ అనుకొనిన రెండవ సంఖ్య ‘x – 36’)
సాధన.
రెండు ధనసంఖ్యలు x, (x – 36) అనుకొనుము.
ఒక దానిని రెండవ దానితో భాగించగా వచ్చు భాగఫలం 4 అయిన
⇒ \(\frac{x}{x-36}\) ⇒ 4 = x = 4(x – 36)
⇒ x = 4x – 144 ⇒ 4x – x = 144
⇒ 3x = 144 ⇒ x = 48
∴ ఆ ధనసంఖ్యలు = x, x – 36 = 48, 12.
ప్రశ్న 4.
ఒక భిన్నంలో లవం, హారం కంటే 4 తక్కువ. అయితే లవ, హారాలకు ఒకటి కలిపిన అది \(\frac {1}{2}\) కు సమానము అవుతుంది. అయిన ఆ భిన్నమును కనుగొనుము.
సాధన.
ఒక భిన్నం \(\frac{x}{y}\) అనుకొనుము.
∴ లవం, హారం కంటే 4 తక్కువ అయిన లవం (x) = y – 4 అగును.
భిన్నం = \(\frac{y-4}{y}\)
లెక్క ప్రకారం \(\frac{y-4+1}{y+1}=\frac{1}{2}\) ⇒ \(\frac{y-3}{y+1}=\frac{1}{2}\)
⇒ 2 = 2(y – 3) = y + 1
⇒ 2(y – 6) = y + 1
⇒ 2y – y = 1 + 6 ⇒ y = 7
∴ కావలసిన భిన్నం = \(\frac{y-4}{y}=\frac{7-4}{7}=\frac{3}{7}\)
ప్రశ్న 5.
మూడు వరుస సంఖ్యలను 10, 17, 26 లచే భాగించినపుడు భాగఫలాల మొత్తం 10ని ఇచ్చే మూడు వరుస సంఖ్యలను కనుగొనుము.
(సూచన : మూడు వరుస సంఖ్యలను x, x + 1, x + 2 అనుకొనిన, \(\frac{x}{10}+\frac{x+1}{17}+\frac{x+2}{26}\) = 10)
సాధన.
మూడు వరుస సంఖ్యలు x, (x + 1), (x + 2) లు అనుకొనుము.,
x, (x + 1), (x + 2) లను 10, 17, 26 లచే
భాగించగా వచ్చు భాగఫలాల మొత్తం 10 అయిన

⇒ 221x + 130x + 130 + 85x + 170 = 22,100
⇒ 436x + 300 = 22,100
⇒ 436x = 22,100 – 300
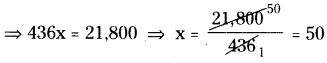
∴ కావలసిన 3 వరుస సంఖ్యలు = 50, 51, 52.
![]()
ప్రశ్న 6.
40 మంది విద్యార్థులు గల తరగతిలో, బాలికల సంఖ్య, బాలుర సంఖ్యలో \(\frac {3}{5}\)వ వంతు అయిన బాలుర సంఖ్యను కనుగొనుము.
సాధన.
తరగతిలోని విద్యార్థుల సంఖ్య = 40
బాలుర సంఖ్య = x అనుకొనుము.
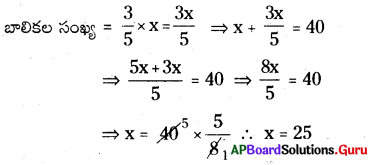
ప్రశ్న 7.
15 సం॥ల తరువాత మేరి వయస్సు, ప్రస్తుత వయస్సుకు 4 రెట్లు. అయిన మేరి ప్రస్తుత వయస్సు ఎంత ?
సాధన.
మేరి ప్రస్తుత వయస్సు = x అనుకొనుము.
15 సం॥ల తరువాత మేరి వయస్సు = (x + 15) సం॥లు
లెక్క ప్రకారం (x + 15) = 4 × x ⇒ x + 15 = 4x
⇒ 4x – x = 15 ⇒ 3x = 15
⇒ x = 5
∴ మేరి ప్రస్తుత వయస్సు = 5 సం॥లు.
ప్రశ్న 8.
అరవింద్ దగ్గర వున్న కిడ్డీ బ్యాంక్ లో రూపాయి నాణెములు, అర్ధ రూపాయి నాణెములు గలవు. అర్ధ రూపాయి నాణెముల సంఖ్య, రూపాయి నాణెముల సంఖ్యకు 3 రెట్లు. నాణెముల మొత్తం విలువ ₹ 35 అయిన ఏఏ రకం నాణెములు ఎన్నెన్ని గలవు ?
సాధన.
రూపాయి నాణేల సంఖ్య = x అనుకొనుము.
అర్ధ రూపాయి నాణేల సంఖ్య = 3 × x = 3x
నాణేల మొత్తం విలువ = ₹ \(\frac{3 x}{2}\) + x
∴ లెక్క ప్రకారం \(\frac{3 x}{2}\) + x = 35
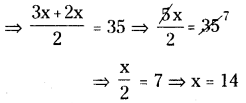
∴ రూపాయి నాణేల సంఖ్య = 14
అర్ధ రూపాయి నాణేల సంఖ్య = 3x = 3 × 14 = 42
ప్రశ్న 9.
A మరియు B లు కలసి ఒక పనిని 12 రోజులలో పూర్తి చేయగలరు. A ఒక్కడే ఆ పనిని 20 రోజులలో పూర్తి చేసిన B ఒక్కడే ఆ పనిని ఎన్ని రోజులలో పూర్తి చేయగలడు ?
సాధన.
A, B లు ఒక పనిని 12 రోజులలో పూర్తి చేయగలిగిన,
వారు ఇరువురూ ఒక రోజులో చేసే పని = \(\frac {1}{2}\)
A అదే పనిని 20 రోజులలో పూర్తి చేయగలిగిన, అతని 1 రోజు పని = \(\frac {1}{20}\)
∴ B ఒక రోజు పని = \(\frac{1}{12}-\frac{1}{20}\)
= \(\frac{5-3}{60}\)
= \(\frac {2}{60}\)
= \(\frac {1}{30}\) వ వంతు
∴ ఆ పనిని పూర్తి చేయుటకు B కి పట్టు రోజులు = 30 రోజులు
![]()
ప్రశ్న 10.
ఒక రైలు 40 కి.మీ./గంట వేగంతో ప్రయాణించిన గమ్యస్థానమును 11 నిమిషాలు ఆలస్యంగా చేరును. ఒకవేళ 50 కి.మీ./గంట వేగంతో ప్రయాణించిన 5 నిమిషాలు ఆలస్యంగా చేరును. అయిన రైలు ప్రయాణించవలసిన దూరమును కనుగొనుము.
సాధన.
చేరవలసిన గమ్యస్థానం యొక్క దూరం = x కి.మీ. అనుకొనుము.
40 కి.మీ./గంట వేగంతో ‘x’ కి.మీ. ప్రయాణించుటకు పట్టు కాలం = \(\frac{x}{40}\) గం॥
50 కి.మీ./గంట వేగంతో ప్రయాణించుటకు పట్టు కాలం = \(\frac{x}{50}\) గం॥
కానీ దత్తాంశం ప్రకారం ఈ రెండింటి మధ్య తేడా = 11 – 5 = 6 ని॥ = \(\frac{6}{60}\) గంటలు
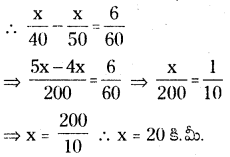
ప్రశ్న 11.
ఒక జింకల గుంపులో \(\frac{1}{4}\)వ భాగము అడవికి వెళ్ళినాయి. మొత్తంలో \(\frac{1}{3}\) వ భాగము పచ్చిక మైదానంలో వున్నాయి. మిగిలిన 15 నది ఒడ్డున నీరు త్రాగుతున్నాయి. అయిన మొత్తం జింకల సంఖ్యను కనుగొనుము.
సాధన.
జింకల సంఖ్య = x అనుకొనుము.
అడవికి వెళ్ళిన జింకల సంఖ్య = \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
పచ్చిక మైదానంలోని జింకల సంఖ్య = \(\frac{1}{4}\) × x = \(\frac{1}{4}\)
∴ మిగిలిన జింకల సంఖ్య =
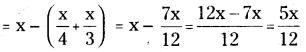
కాని, లెక్క ప్రకారం మిగిలిన జింకల సంఖ్య = 15
∴ \(\frac{5 x}{12}\) = 15
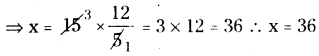
∴ మొత్తం జింకల సంఖ్య = 36
ప్రశ్న 12.
ఒక దుకాణదారుడు ఒక రేడియోను ₹ 903 లకు అమ్మటం వల్ల అతను 5% లాభాన్ని పొందుతాడు. అయిన రేడియో యొక్క కొన్నవెలను కనుగొనుము.
సాధన.
రేడియో అమ్మినవెల (S.P.) = ₹ 903
లాభశాతం = 5%
కోన్నవెల (C.P.) = ?

![]()
ప్రశ్న 13.
శేఖర్ తన వద్ద వున్న మిఠాయిలలో పావు భాగము రేణుకు, 5 మిఠాయిలు రాజికి ఇచ్చాడు. ఇంకా తన వద్ద 7 మిఠాయిలు మిగిలి వున్న అతని వద్ద మొదట వున్న మిఠాయిలు ఎన్ని ?
సాధన.
శేఖర్ వద్ద వున్న మిఠాయిల సంఖ్య = x అనుకొనుము.
రేణుకకు ఇచ్చిన భాగం = \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
రాజికి ఇచ్చిన మిఠాయిల సంఖ్య = 5
ఇంకా తన వద్ద నున్న మిఠాయిల సంఖ్య = 7
లెక్క ప్రకారం
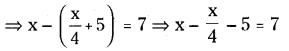

∴ శేఖర్ వద్ద మొదట ఉన్న మిఠాయిల సంఖ్య = 16