AP Board 8th Class Maths Solutions Chapter 4 ఘాతాంకాలు మరియు ఘాతాలు Ex 4.1

SCERT AP 8th Class Maths Solutions Chapter 4 ఘాతాంకాలు మరియు ఘాతాలు Ex 4.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు Exercise 4.1

1. సూక్ష్మీకరించి తగు కారణాలు తెలుపుము.
(i) 4^-3
(ii) (-2)⁷
(iii) \(\left(\frac{3}{4}\right)^{-3}\)
(iv) (-3)^-4
సాధన.
(i) 4^-3 = \(\frac{1}{4^{3}}=\frac{1}{64}\)
[∵ \(a^{-n}=\frac{1}{a^{n}}\)]

(ii) (-2)⁷ = – (2)⁷ = – 128 [∵ 7 బేసిసంఖ్య]
ఎందుకనగా (-a)ⁿ విస్తరణలో n బేసిసంఖ్య అయిన (-a)ⁿ = – aⁿ అగును.

(iii) \(\left(\frac{3}{4}\right)^{-3}\)

(iv) (3)^-4 = \(\frac{1}{(-3)^{4}}\) [∵ \(a^{-n}=\frac{1}{a^{n}}\)]
= \(\frac{1}{3^{4}}\) [∵ 4 ఒక సరిసంఖ్య]
= \(\frac {1}{81}\)

2. కింది వానిని సూక్ష్మీకరింపుము.
(i) \(\left(\frac{1}{2}\right)^{4} \times\left(\frac{1}{2}\right)^{5} \times\left(\frac{1}{2}\right)^{6}\)
సాధన.
\(\left(\frac{1}{2}\right)^{4+5+6}=\left(\frac{1}{2}\right)^{15}\)
= \(\frac{1}{2^{15}}\) [∵ a^m × aⁿ = a^m+n]

(ii) (-2)⁷ × (-2)³ × (-2)⁴
సాధన.
(-2)⁷⁺³⁺⁷ = (-2)¹⁴ = 2¹⁴
[∵ (-a)ⁿ = aⁿ, n ఒక సరిసంఖ్య ]

(iii) 4⁴ × \(\left(\frac{5}{4}\right)^{4}\)
సాధన.
\(4^{4} \times \frac{5^{4}}{4^{4}}=5^{4}\)
[∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\)]

(iv) \(\left[\frac{5^{-4}}{5^{-6}}\right] \times 5^{3}\)
సాధన.
= 5^-4 × (5⁶ × 5³) [∵ \(\frac{1}{a^{-n}}=a^{n}\)]
= 5^-4 × 5⁶⁺³ [∵ a^m × aⁿ = a^m+n]
= 5^-4 × 5⁹ = 5^(-4)+9 = 5⁵

(v) (-3)⁴ × 7⁴
సాధన.
= 3⁴ × 7⁴ [∵ 4 ఒక సరి సంఖ్య ]
= (3 × 7)⁴ = (21)⁴ [∵ a^m × b^m = (ab)^m]

3. సూక్ష్మీకరింపుము.
(i) \(2^{2} \times \frac{3^{2}}{2^{-2}} \times 3^{-1}\)
సాధన.
= 2² × 2² × 3² ×3^-1 [∵ \(\frac{1}{a^{-n}}=a^{n}\)]
= 2²⁺² × 3^2+(-1)
= 2⁴ × 3¹ = 16 × 3 = 48

(ii) (4^-1 × 3^-1) ÷ 6^-1
సాధన.
= \(\left(\frac{1}{4} \times \frac{1}{3}\right) \div \frac{1}{6}\) [∵ \(a^{-n}=\frac{1}{a^{n}}\)]
= \(\frac{1}{12}+\frac{1}{6}\)
= \(\frac {6}{12}\)
= \(\frac {1}{2}\)
= 2^-1

4. సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
(i) (4⁰ + 5^-1) × 5² × \(\frac {1}{3}\)
సాధన.

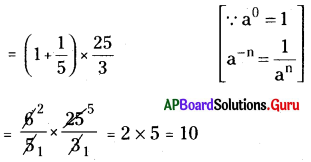
(ii) \(\left(\frac{1}{2}\right)^{-3} \times\left(\frac{1}{4}\right)^{-3} \times\left(\frac{1}{5}\right)^{-3}\)
సాధన.

(iii) (2^-1 + 3^-1 + 4^-1) × \(\frac {3}{4}\)
సాధన.

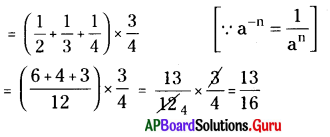
(iv) \(\frac{3^{-2}}{3} \times\left(3^{0}-3^{-1}\right)\)
సాధన.

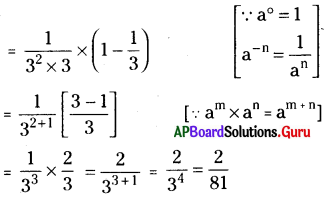
(v) 1 + 2^-1 + 3^-1 + 4⁰
సాధన.

(vi) \(\left[\left(\frac{3}{2}\right)^{-2}\right]^{2}\)
సాధన.

5. సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
(i) \(\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}\)
(ii) ((5²)³ × 5⁴) ÷ 5⁶
సాధన.
(i) \(\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}\)
= \(\left[5 \times \frac{5}{1}\right]^{2}\)
= (5²)² = 5⁴ = 625 [∵ (a^m)ⁿ = a^mn]

(ii) ((5²)³ × 5⁴) ÷ 5⁶
సాధన.

6. కింది వానిలో ‘n’ విలువను కనుగొనుము.
(i) \(\left(\frac{2}{3}\right)^{3} \times\left(\frac{2}{3}\right)^{5}=\left(\frac{2}{3}\right)^{n-2}\)
సాధన.

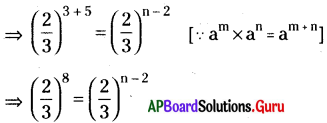
భూములు సమానమైన ఘాతాంకాలు సమానాలు.
⇒ n – 2 = 8 ⇒ n = 8 + 2 = 10
∴ n = 10

(ii) (-3)ⁿ⁺¹ × (-3)⁵ = (-3)^-4
సాధన.
⇒ (-3)ⁿ⁺¹⁺⁵ = (-3)^-4 [∵ a^m x aⁿ = a^m+n]
⇒ (-3)ⁿ⁺⁶ = (-3)^-4
⇒ n + 6 = -4
n = – 4 – 6 = – 10
∴ n = – 10

(iii) 7²ⁿ⁺¹ ÷ 49 = 7³
సాధన.

7. 2^-3 = \(\frac{1}{2^{x}}\) అయిన x విలువను కనుగొనుము.
సాధన.
2^-3 = \(\frac{1}{2^{x}}\) = 2^-x [∵ \(\frac{1}{a^{n}}=a^{-n}\)]
⇒ 2^-3 = 2^-x
⇒ -x = -3
∴ x = 3

8. \(\left[\left(\frac{3}{4}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\right] \times\left(\frac{3}{5}\right)^{-2}\) సూక్ష్మీకరించుము.
సాధన.

9. m = 3 మరియు n = 2 అయిన ఈ క్రింది వాని విలువలను కనుగొనుము.
i) 9m² – 10n³
ii) am²n²
iii) 2m³ + 3n² – 5m²n
iv) mⁿ – n^m
సాధన.
i) 9m² – 10n³ = 9(3)² – 10(2)³
= 9 × 9 – 10 × 8
= 81 – 80 = 1

ii) 2m²n²
= 2(3)²(2)²
= 2 × 9 × 4
= 72

iii) 2m³ + 3n² – 5m²n
= 2(3)³ + 3(2)² – 5(3)² × 2
= (2 × 27) + (3 × 4) – (5 × 9 × 2)
= 54 + 12 – 90
= 66 – 90
= – 24

iv) mⁿ – n^m = 3² – 2³
= 3 × 3 – 2 × 2 × 2 = 9 – 8 = 1

10. \(\left(\frac{4}{7}\right)^{-5} \times\left(\frac{7}{4}\right)^{-7}\) సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
సాధన.