AP Inter 2nd Year Maths 2A Solutions Chapter 9 సంభావ్యత Ex 9(b)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 9 సంభావ్యత Exercise 9(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 9 సంభావ్యత Exercise 9(b)

అభ్యాసం – 9(బి)

I.

ప్రశ్న 1.
నాలుగు నిష్పాక్షిక నాణేలను ఒకేసారి ఎగురవేసినప్పుడు 2 బొమ్మలు, 2 బొరుసులు పడే సంభావ్యతను కనుక్కోండి. [Mar. ’02]
సాధన:
4 నాణేలను ఒకేసారి ఎగురవేశారు.
∴ n(S) = 2⁴ = 16
E అనేది రెండు బొమ్మలు, రెండు బొరుసులు రావటం అనే ఘటన
n(E) = ⁴C₂
= \(\frac{4 \times 3}{1 \times 2}\)
= 6
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{6}{16}=\frac{3}{8}\)

ప్రశ్న 2.
లీపు సంవత్సరం కాని సందర్భంలో (i) 53 ఆదివారాలు (ii) 52 ఆదివారాలు మాత్రమే వచ్చే సంభావ్యతను కనుక్కోండి. [Mar. ’07, May ’06]
సాధన:
లీపు సంవత్సరం కాని సాధారణ సంవత్సరంలో 365 రోజులుంటాయి. అంటే 52 వారాలు పోగా, ఒకరోజు మిగులుతుంది.
ఆ ఒక్కరోజు ఆది (లేక) సోమ (లేక) మంగళ (లేక) బుధ (లేక) గురు (లేక) శుక్ర (లేక) శనివారం కావచ్చు.
∴ శాంపిల్ ఆవరణ S = {ఆది, సోమ, మంగళ, బుధ, గురు, శుక్ర, శని}
n(S) = 7
(i) E అనేది సాధారణ సంవత్సరంలో 53 ఆదివారాలు ఉండే ఘటన
n(E) = 1
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{1}{7}\)
(ii) ఇక 52 ఆదివారాలు మాత్రమే ఉండే ఘటన సంభావ్యత
P(E^C) = 1 – P(E)
= 1 – \(\frac{1}{7}\)
= \(\frac{6}{7}\)

ప్రశ్న 3.
రెండు పాచికలను దొర్లించారు. ఏ పాచిక 2 ను చూపని సందర్భానికి సంభావ్యత ఎంత?
సాధన:
రెండు పాచికలను దొర్లించారు.
కనుక n(S) = 6² = 36
E అనేది ఏ పాచిక 2 చూపని ఘటన
n(E) = 5 × 5 = 25
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{25}{36}\)

ప్రశ్న 4.
ఒక చీట్లపేక కట్ట నుంచి యాదృచ్ఛికంగా ఒక పేక ముక్కను తీసే ప్రయోగంలో ఇస్ఫేటు ముక్కను తీసే ఘటనను తోను, బొమ్మను కలిగిన కార్డును (రాజు, రాణి లేదా జాకీ) తీసే ఘటనను B తోనూ సూచిద్దాం. అప్పుడు A, B, (A ∩ B), (A ∪ B) ల సంభావ్యతను కనుక్కోండి.
సాధన:
చీట్ల పేక కట్ట నుంచి ఒక పేకను తీసితిరి.
∴ n(S) = ⁵²C₁ = 52
(i) A అనేది తీసిన పేక ముక్క ఇస్ఫేటు కావటం అనే ఘటన
∴ n(A) = ¹³C₁ = 13
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{13}{52}=\frac{1}{4}\)
(ii) B అనేది బొమ్మను కలిగిన కార్డును తీసే ఘటన
∴ n(B) = ¹²C₁ = 12
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{12}{52}=\frac{3}{13}\)
(iii) ఘటన A ∩ B అనేది తీసిన కార్డు బొమ్మను కలిగిన ఇస్ఫేటు కార్డు కావటం అనే ఘటన
∴ n(A ∩ B) = 3
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{3}{52}\)
(iv) ఘటన A ∪ B అనేది తీసిన పేక ముక్క ఇస్ఫేటు లేదా బొమ్మను కలిగిన కార్డు కావడం అనే ఘటన
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{1}{4}+\frac{3}{13}-\frac{3}{52}\)
= \(\frac{13+12-3}{52}\)
= \(\frac{22}{52}\) లేదా \(\frac{11}{26}\)

ప్రశ్న 5.
60 బాలురు, 20 బాలికలు గల తరగతిలో సగం మంది బాలురు, సగం మంది బాలికలు క్రికెట్పై అవగాహన కలిగినవారు. ఈ తరగతి నుంచి ఒక విద్యార్థిని ఎంపిక చేసినప్పుడు, బాలుడు లేదా క్రికెట్ తెలిసిన వ్యక్తి అయ్యే ఘటనకు సంభావ్యతను కనుక్కోండి.
సాధన:
ఎంపిక చేసినవాడు బాలుడు అయ్యే ఘటన A, ఎంపిక చేసినవారు క్రికెట్ తెలిసిన వ్యక్తి అయ్యే ఘటన B అనుకుందాం.
n(S) = ^{(60 + 20)}C₁ = 80
n(A) = 60, n(B) = (30 + 10) = 40
(∵ సగం మంది బాలురు, సగం మంది బాలికలకు క్రికెట్పై అవగాహన ఉంది.)
A ∩ B అనేది క్రికెట్ తెలిసిన బాలుడు కావటం అనే ఘటన అవుతుంది.
∴ n(A ∩ B) = 30 (సగం మంది బాలురకు క్రికెట్పై అవగాహన ఉంది).
∴ P(A) = \(\frac{60}{80}\), P(B) = \(\frac{40}{80}\), P(A ∩ B) = \(\frac{30}{80}\)
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{60}{80}+\frac{40}{80}-\frac{30}{80}\)
= \(\frac{70}{80}\)
= \(\frac{7}{8}\)

ప్రశ్న 6.
రెండు ఘటనలు A, B లకు P(A^C ∩ B^C) = 1 + P(A ∩ B) – P(A) – P(B) అని చూపండి.
సాధన:
A^C ∩ B^C = (A ∪ B)^C కనుక
P(A^C ∩ B^C) = P[(A ∪ B)^C]
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 + P(A ∩ B) – P(A) – P(B)
∴ P(A^C ∩ B^C) = 1 + P(A ∩ B) – P(A) – P(B)

ప్రశ్న 7.
‘ముందుగా 3ను దొర్లించిన వాళ్ళు ఆట గెలిచినట్లు’ అనే షరతుపై A, B అనే ఇద్దరు వ్యక్తులు పాచిక దొర్లించారు. ఆటను ముందుగా A మొదలు పెడితే, A, B లు వరుసగా ఆట గెలిచే సంభావ్యతను కనుక్కోండి.
సాధన:
పాచికను దొర్లించినపుడు ‘3’ చుక్కలున్న ముఖం తిరగబడుటకు సంభావ్యత p = \(\frac{1}{6}\)
∴ సఫల సంభావ్యత p = \(\frac{1}{6}\)
విఫల సంభావ్యత q = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
A గెలిచే ఘటన జరగాలంటే
1. మొదటి యత్నంలోనే A గెలవాలి (ఈ ఘటన సంభావ్యత p) లేదా
2. మొదటి రెండు యత్నాలలో A, B లు ఓడిపోయి, తరువాత యత్నంలో A గెలవాలి.
ఈ ఘటన సంభావ్యత = q . q . p = q²p లేదా
3. మొదటి నాలుగు యత్నాలలో A, B లు ఓడిపోయి ఆ తరువాత యత్నంలో A గెలవాలి.
ఈ ఘటన సంభావ్యత = q . q . q . q . p = q⁴ . p ……
ఈ విధంగా A పాచికపై ‘3’ చుక్కలు వచ్చేవరకు ఆట కొనసాగుతుంది.
పై ఘటనలన్నీ పరస్పర వివర్జితాలు.
∴ సంకలన సిద్ధాంతం నుంచి A గెలుపు సంభావ్యత
P(A) = p + q²p + q⁴P + …..
= p[1 + q² + q⁴ + …..]

∴ B గెలుపు సంభావ్యత = 1 – P(A) = 1 – \(\frac{6}{11}\) = \(\frac{5}{11}\)

ప్రశ్న 8.
A, B, C లు ఒక పట్టణం నుంచి వెలువడే వార్తాపత్రికలు. ఆ పట్టణ జనాభాలో 20% Aని, 16% Bని, 14% C ని, 8% A, B రెండింటిని, 5% A, C రెండింటిని, 4% B, C రెండింటిని, 2% మూడింటినీ చదువుతారు. కనీసం ఒక వార్తాపత్రికను చదివే జనాభా శాతాన్ని కనుక్కోండి.
సాధన:
P(A) = \(\frac{20}{100}\) = 0.2
P(B) = \(\frac{20}{100}\) = 0.16
P(C) = \(\frac{14}{100}\) = 0.14
P(A ∩ B) = \(\frac{8}{100}\) = 0.08
P(B ∩ C) = \(\frac{4}{100}\) = 0.04
P(C ∩ A) = \(\frac{5}{100}\) = 0.05
P(A ∩ B ∩ C) = \(\frac{2}{100}\) = 0.02
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
= 0.2 + 0.16 + 0.14 – 0.08 – 0.04 – 0.05 + 0.02
= 0.52 – 0.17
= 0.35
= \(\frac{35}{100}\)
∴ జనాభాలో కనీసం ఒక పత్రికైనా చదివేవారు = 35%

ప్రశ్న 9.
1 నుంచి 30 వరకు సంఖ్యలను వేసిన 30 టిక్కెట్ల నుంచి యాదృచ్ఛికంగా ఒక టిక్కెట్ను ఎంపికచేస్తే, ఆ టిక్కెట్పై గల సంఖ్య (i) 5 లేదా 7 గుణిజం (ii) 3 లేదా 5 గుణిజం కాగల సంభావ్యతను కనుక్కోండి. [Mar. ’08]
సాధన:
1 నుండి 30 వరకు అంకెలున్న 30 టిక్కెట్ల నుండి యాదృచ్ఛికంగా ఒక టిక్కెట్ ఎన్నుకునే విధాల సంఖ్య
n(S) = ³⁰C₁ = 30
(i) E₁ అనేది ఆ అంకె 5 యొక్క గుణిజం కావటం అనే ఘటన
E₁ = {5, 10, 15, 20, 25, 30}
n(E₁) = 6
P(E₁) = \(\frac{\mathrm{n}\left(E_1\right)}{\mathrm{n}(S)}=\frac{6}{30}=\frac{1}{5}\)
E₂ అనేది ఆ అంకె 7 యొక్క గుణిజం కావటం అనే ఘటన
E₂ = {7, 14, 21, 28}
n(E₂) = 4
P(E₂) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{4}{30}\)
∵ E₁ ∩ E₂ = φ
P(E₁ ∪ E₂) = P(E₁) + P(E₂)
= \(\frac{6}{30}+\frac{4}{30}\)
= \(\frac{10}{30}\)
= \(\frac{1}{3}\)
(ii) E₁ అనేది అంకె 3 యొక్క గుణిజం కావటం అనే ఘటన
E₁ = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
n(E₁) = 10
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}=\frac{10}{30}\)
E₂ అనేది అంకె 5 యొక్క గుణిజం కావటం అనే ఘటన
E₂ = {5, 10, 15, 20, 25, 30)
n(E₂) = 6
P(E₂) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{6}{30}\)
E₁ ∩ E₂ = {15, 30}
P(E₁ ∩ E₂) = \(\frac{2}{30}\)
P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
= \(\frac{10}{30}+\frac{6}{30}-\frac{2}{30}\)
= \(\frac{14}{30}\)
= \(\frac{7}{15}\)

ప్రశ్న 10.
20 వరస సహజ సంఖ్యల నుంచి రెండు సంఖ్యలను యాదృచ్ఛికంగా ఎంపిక చేస్తే, ఆ రెండు సంఖ్యల మొత్తం (i) ఒక సరిసంఖ్య కావడానికి (ii) ఒక బేసి సంఖ్య కావడానికి సంభావ్యతను కనుక్కోండి.
సాధన:
20 వరస సహజ సంఖ్యల నుంచి 2 సంఖ్యలను ఎంపిక చేసే విధానాలు
n(S) = ²⁰C₂
= \(\frac{20 \times 19}{1 \times 2}\)
= 190
వీటిలో 10 బేసిసంఖ్యలు, 10 సరిసంఖ్యలు
(i) E అనేది ఎంపిక చేసిన రెండు సంఖ్యల మొత్తం సరి సంఖ్య కావాలి అనే ఘటన.
రెండు బేసి సంఖ్యల మొత్తం సరి సంఖ్య అవుతుంది లేదా రెండు సరి సంఖ్యల మొత్తం సరి సంఖ్య అవుతుంది.
∴ n(E) = ¹⁰C₂ + ¹⁰C₂
= \(\frac{2(10)(9)}{1 \times 2}\)
= 90
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{90}{190}=\frac{9}{19}\)
(ii) ఎంపిక చేసిన రెండు సంఖ్యల మొత్తం బేసిసంఖ్య కావడానికి సంభావ్యత
P(E^C) = 1 – P(E)
= 1 – \(\frac{9}{19}\)
= \(\frac{10}{19}\)

ప్రశ్న 11.
ఒక నాణేన్ని 3 సార్లు ఎగరవేయడం, వచ్చిన ఫలితాన్ని రాయడం ఒక క్రీడ. అన్ని ఎగరవేతలలోనూ, ఒకే ఫలితం వస్తే ఒక బాలుడు గెలిచినట్లు, అట్లా కాకపోతే ఓడినట్లు భావిస్తారు. ఆ బాలుడు క్రీడలో ఓడిపోయే సంభావ్యతను కనుక్కోండి.
సాధన:
ఒక నాణేన్ని 3 సార్లు ఎగరవేస్తే n(S) = 2³ = 8
అన్ని ఎగరవేతలలోనూ, ఒకే ఫలితం వస్తే, అంటే అన్ని బొమ్మలు లేదా అన్ని అచ్చులు వస్తే బాలుడు గెలిచినట్లుగా భావిస్తారు.
కనుక బాలుడు గెలిచే ఘటన E అయితే
P(E) = \(\frac{2}{8}=\frac{1}{4}\)
∵ E = {HHH, TTT}
∴ ఆ బాలుడు క్రీడలో ఓడిపోయే సంభావ్యత
P(E^C) = 1 – P(E)
= 1 – \(\frac{1}{4}\)
= \(\frac{3}{4}\)

ప్రశ్న 12.
E₁ ∩ E₂ = φ తో E₁, E₂, రెండు ఘటనలు. అప్పుడు \(P\left(E_1^c \cap E_2^c\right)=P\left(E_1^c\right)-P\left(E_2\right)\) అని చూపండి.
సాధన:
E₁ ∩ E₂ = φ
⇒ E₁, E₂ లు పరస్పర వివర్జిత ఘటనలు కనుక
E₁ ∩ E₂ = φ
ఇప్పుడు \(P\left(E_1^c \cap E_2^c\right)\) = P[(E₁ ∪ E₂)^C]
= 1 – P(E₁ ∪ E₂)
= 1 – [P(E₁) + P(E₁)] (∴ E₁, E₂ పరస్పర వివర్జిత ఘటనలు)
= 1 – P(E₁) – P(E₂)
= [1 – P(E₁)] – P(E₂)
= \(P\left(E_1^c\right)\) – P(E₂)

II.

ప్రశ్న 1.
ఒక జత పాచికలను 24 సార్లు దొర్లించారు. ఈ 24 పర్యాయాలలో ఎప్పుడూ ఒక జత 6ను దొర్లించని వ్యక్తి గెలిచినట్లుగా భావిస్తారు. ఆ వ్యక్తి గెలిచే సంభావ్యత ఎంత?
సాధన:
పాచికను 2 సార్లు దొర్లిస్తే పూర్ణ లఘు ఘటనల సంఖ్య = 6 × 6 = 36
రెండు పాచికలను 24 సార్లు దొర్లించారు కనుక n(S) = (36)²⁴
E అనేది దొర్లించిన 24 సార్లలో ఏ ఒక్కసారీ రెండింటిపై 6 రాకపోవటం అనే ఘటన
n(E) = 35 × 35 × ……. × 35 (24 సార్లు) = (35)²⁴
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{(35)^{24}}{(36)^{24}}=\left(\frac{35}{36}\right)^{24}\)

ప్రశ్న 2.
P ఒక సంభావ్యతా ప్రమేయం అయితే, ఏదైనా రెండు ఘటనలు A, B లకు P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ≤ P(A) + P(B) అని చూపండి.
సాధన:

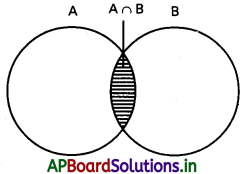
ఏవేని రెండు సమితులు A, B లకు
A ∩ B ⊆ A ⊆ A ∪ B
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ……(1)
సంభావ్యతల సంకలన సిద్ధాంతం నుండి
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∴ 0 ≤ P(A ∩ B) ≤ 1
⇒ P(A ∪ B) ≤ P(A) + P(B) ……(2)
∴ (1), (2) ల నుండి
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ≤ P(A) + P(B)

ప్రశ్న 3.
ఒక పెట్టెలోని 15 బల్బులలో 5 పనిచేయనివి. పెట్టెలో నుంచి యాదృచ్ఛికంగా 5 బల్బులను తీసినప్పుడు, క్రింది ఘటనల సంభావ్యతను కనుక్కోండి.
(i) వాటిలో ఏదీ లోపం లేనిది కావటం అనేది
(ii) వాటిలో ఏదో ఒకటి పని చేయనిది
(iii) వాటిలో కనీసం ఒకటి పనిచేయనిది.
సాధన:
పెట్టెలో ఉన్న 15 బల్బులలో 5 పనిచేయనివి కలిగి ఉన్నవి. మిగిలిన 10 మంచివి.
పెట్టె నుండి యాదృచ్ఛికంగా 5 బల్బులను ఎన్నుకునే విధాలు n(S) = ¹⁵C₅
(i) E₁ అనేది 5 బల్బులు ఏదీ లోపం లేనిది అనే ఘటన అంటే అన్నీ మంచివి కావటం అనే ఘటన
n(E₁) = ¹⁰C₅

ప్రశ్న 4.
A, B లు IIT లో ప్రవేశం కోరుకుంటున్నారు. A ఎంపిక కాగల సంభావ్యత 0.5, ఇద్దరూ ఎంపిక కాగల సంభావ్యత 0.3 అయితే, B ఎంపిక కాగల సంభావ్యత 0.9 అయ్యే అవకాశం ఉందా?
సాధన:
P(A) = 0.5; P(A ∩ B) = 0.3
∵ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ P(A ∪ B) = 0.5 + P(B) – 0.3
⇒ P(A ∪ B) = 0.2 + P(B) [∵ P(A ∪ B) ≤ 1]
⇒ 0.2 + P(B) ≤ 1
⇒ P(B) ≤ 0.8
కనుక P(B) = 0.9 కావడం అసాధ్యం.

ప్రశ్న 5.
ఒక కాంట్రాక్టరు రోడ్డు కాంట్రాక్టును పొందే సంభావ్యత \(\frac{2}{3}\), భవనం కాంట్రాక్టును పొందే సంభావ్యత \(\frac{5}{9}\), కనీసం ఒక కాంట్రాక్టునైనా పొందే సంభావ్యత \(\frac{4}{5}\). అతడు రెండు కాంట్రాక్టులనూ పొందే సంభావ్యతను కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
కాంట్రాక్టరు రోడ్డు కాంట్రాక్టు పొందటానికి సంభావ్యత
P(A) = \(\frac{2}{3}\)
భవనం కాంట్రాక్టు పొందడానికి సంభావ్యత
P(B) = \(\frac{5}{9}\)
కనీసం ఒకటి పొందటానికి సంభావ్యత
P(A ∪ B) = \(\frac{4}{5}\)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
రెండు కాంట్రాక్టులనూ పొందటానికి సంభావ్యత
∴ P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= \(\frac{2}{3}+\frac{5}{9}-\frac{4}{5}\)
= \(\frac{30+25-36}{45}\)
= \(\frac{19}{45}\)

ప్రశ్న 6.
25 మంది సభ్యులు గల ఒక కమిటీలో ప్రతి సభ్యుడు గణితంలో గానీ, సాంఖ్యక శాస్త్రంలో గానీ లేదా రెండింటిలో గానీ ప్రవీణులై ఉంటారు. వీరిలో 19 మంది గణితం లోనూ, 16 మంది సాంఖ్యకశాస్త్రంలోనూ ప్రవీణులైతే, కమిటీ నుంచి ఎంపిక చేసిన ఒక సభ్యుడు రెండింటిలోనూ ప్రవీణుడై ఉండే సంభావ్యతను కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
ఎన్నుకొన్న వ్యక్తి గణితంలో ప్రవీణుడయ్యే ఘటన = M
సాంఖ్యకశాస్త్ర ప్రవీణుడయ్యే ఘటన = S అనుకుందాం.
P(M) = \(\frac{19}{25}\), P(S) = \(\frac{16}{25}\)
ప్రతివారూ ఏదో ఒక శాస్త్రంలో ప్రవీణులు.
∴ M ∪ S ఒక నిశ్చిత ఘటన, P(M ∪ S) = 1
సంభావ్యతల సంకలన సిద్ధాంతం నుండి
P(M ∪ S) = P(M) + P(S) – P(M ∩ S)
∴ P(M ∩ S) = \(\frac{19}{25}+\frac{16}{25}\) – 1
= \(\frac{35}{25}\) – 1
= \(\frac{10}{25}\)
= \(\frac{2}{5}\)
∴ ఎన్నుకొన్న వ్యక్తి రెండు శాస్త్రాల్లోనూ ప్రవీణుడయ్యే ఘటన సంభావ్యత = \(\frac{2}{5}\)

ప్రశ్న 7.
ఒక పరుగు పందెంలో A, B, C మూడు గుర్రాలు. A పందెం గెలిచే సంభావ్యత B సంభావ్యతకు రెట్టింపు, B పందెం గెలిచే సంభావ్యత C గెలుపుకి రెట్టింపు అయితే, A, B, C లు ఆ పందెం గెలవగల సంభావ్యతలేవి? [Mar. ’14, ’13]
సాధన:
ఇచ్చట A, B, C లు పరస్పర వివర్జిత ఘటనలు
P(A) + P(B) + P(C) = 1 ……(1)
దత్తాంశము నుంచి P(A) = 2P(B), P(B) = 2P(C) ……..(2)
(1), (2)ల నుంచి
2P(B) + P(B) + P(C) = 1
⇒ 3P(B) + P(C) = 1
⇒ 3 (2) P(C) + P(C) = 1
⇒ 7 P(C) = 1
⇒ P(C) = \(\frac{1}{7}\)
∴ P(C) = \(\frac{1}{7}\), P(B) = \(\frac{2}{7}\), P(A) = \(\frac{4}{7}\)

ప్రశ్న 8.
ఒక సంచిలో 12 రెండు రూపాయి నాణేలు, 7 రూపాయి నాణేలు, 4 అర్ధరూపాయి నాణేలు ఉన్నాయి. ఆ సంచి నుంచి యాదృచ్ఛికంగా మూడు నాణేలను ఎంపిక చేస్తే,
(i) మూడు నాణేల మొత్తం గరిష్టం కావడానికి
(ii) మూడు నాణేల మొత్తం కనిష్ఠం కావడానికి
(iii) మూడు నాణేలు వేర్వేరు విలువలను కలిగి ఉండటానికి గల సంభావ్యతలను కనుక్కోండి.
సాధన:
సంచిలోని నాణేల సంఖ్య = 12 + 7 + 4 = 23
వాటి నుండి యాదృచ్ఛికంగా 3 నాణేలను ఎన్నుకొనే విధాల సంఖ్య n(S) = ²³C₃
(i) E₁ అనేది ఎన్నుకున్న 3 నాణేల మొత్తం గరిష్టం కావడం అనే ఘటన అంటే మూడు రెండు రూపాయి నాణేలు కావాలి.
అందువలన n(E₁) = ¹²C₃
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}=\frac{{ }^{12} C_3}{{ }^{23} C_3}\)
(ii) E₂ అనేది ఎన్నుకున్న 3 నాణేల మొత్తం కనిష్టం కావడం అనే ఘటన అంటే మూడు నాణేలు అర్థరూపాయి నాణేలు కావాలి.
n(E₂) = ⁴C₃
P(E₂) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{{ }^4 C_3}{{ }^{23} C_3}\)
(iii) E₃ అనేది ఒక్కొక్కటి ఒక్కో రకం నాణెం కావడం అనే ఘటన
n(E₃) = ¹²C₁ × ⁷C₁ × ⁴C₁ = 12 × 7 × 4
P(E₃) = \(\frac{n\left(E_3\right)}{n(S)}=\frac{12 \times 7 \times 4}{{ }^{23} C_3}\)

ప్రశ్న 9.
మూడు ఘటనలు A, B, C ల సంభావ్యతలు క్రింది విధంగా ఉన్నాయి.
P(A) = 0.3, P(B) = 0.4, P(C) = 0.8, P(A ∩ B) = 0.08, P (A ∩ C) = 0.28, P(A ∩ B ∩ C) = 0.09, P(A ∪ B ∪ C) ≥ 0.75. P(B ∩ C) అంతరం [0.23, 0.48] లో ఉంటుందని చూపండి.
సాధన:
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
⇒ P(A ∪ B ∪ C) = 0.3 + 0.4 + 0.8 – 0.08 – 0.28 – P(B ∩ C) + 0.09
= 1.59 – 0.36 – P(B ∩ C)
= 1.23 – P(B ∩ C)
దత్తాంశం నుంచి 0.75 ≤ P(A ∪ B ∪ C) ≤ 1
⇒ 0.75 ≤ 1.23 – P(B ∩ C) ≤ 1
⇒ -0.48 ≤ -P(B ∩ C) ≤ -0.23
⇒ 0.23 ≤ P(B ∩ C) ≤ 0.48
∴ P(B ∩ C) ∈ [0.23, 0.48]

ప్రశ్న 10.
మూడు పరస్పర వివర్జిత ఘటనల సంభావ్యతలు వరుసగా \(\frac{1+3 P}{3}, \frac{1-P}{4}, \frac{1-2 P}{2}\) అయితే \(\frac{-1}{3} \leq P \leq \frac{1}{2}\) అని నిరూపించండి.
సాధన:
ఇచ్చిన దత్తాంశం ప్రకారం,
∴ 0 ≤ \(\frac{1+3 P}{3}\) ≤ 1
⇒ 0 ≤ 1 + 3P ≤ 3
⇒ -1 ≤ 3P ≤ 2
⇒ \(\frac{-1}{3} \leq P \leq \frac{2}{3}\) ……….(1)
∴ 0 ≤ \(\frac{1-P}{4}\) ≤ 1
⇒ 0 ≤ 1 – P ≤ 4
⇒ -1 ≤ -P ≤ 3
⇒ 1 ≥ P ≥ -3
⇒ -3 ≤ P ≤ 1 …….(2)
∴ 0 ≤ \(\frac{1-2 P}{2}\) ≤ 1
⇒ 0 ≤ 1 – 2P ≤ 2
⇒ -1 ≤ -2P ≤ 1
⇒ 1 ≥ 2P ≥ -1
⇒ -1 ≤ 2P ≤ 1
⇒ \(\frac{-1}{2} \leq P \leq \frac{1}{2}\) ………(3)
(1), (2), (3) ల నుండి \(\frac{-1}{3} \leq P \leq \frac{1}{2}\)

ప్రశ్న 11.
ఒకడు పండుగరోజు A, B, C, D అనే 4 దేవాలయాలను యాధృచ్ఛిక క్రమంలో దర్శించుకోవాలనుకుంటాడు. అతడు (i) Bకి ముందుగా A (ii) B కి ముందుగా A మరియు Cకి ముందుగా B లను దర్శించుకొనే సంభావ్యతలను కనుక్కోండి.
సాధన:
(i) A, B, C, D లు కుర్చిలలో B కి ముందుగా A కూర్చొనే విధంగా దేవాలయాలు దర్శించుకొనుట, ముందుగా C, D లు 4 కుర్చీలలో కూర్చొనగల విధానాలు సంఖ్య ⁴P₂ = 12
మరియు మిగిలిన రెండు కుర్చీలలో B కి ముందుగా A కూర్చొనే విధానాల సంఖ్య 1.
n(S) = 24
B కి ముందుగా A దేవాలయం దర్శించుకొనే సంభావ్యత
B = \(\frac{12 \times 1}{24}=\frac{1}{2}\)
(i) మాదిరిగా ముందుగా D ను 4 కుర్చీలలో కూర్చొనగల విధానాల సంఖ్య 4.
మిగిలిన మూడు కుర్చీలలో Bకి ముందుగా A మరియు C కి ముందుగా B కూర్చొనగల విధానాల సంఖ్య.
n(S) = 4! = 24
∴ B కి ముందుగా A మరియు C కి ముందుగా B దేవాలయాలను దర్శించుకొనే సంభావ్యత = \(\frac{4 \times 1}{24}=\frac{1}{6}\)

ప్రశ్న 12.
ఒక కంపెనీలోని ఉద్యోగుల నుంచి 5 గురు వ్యక్తులను ఈ కంపెనీ పాలకవర్గ ప్రతినిధులుగా ఎన్నుకొన్నారు. 5గురు వ్యక్తుల వివరాలు క్రింది విధంగా వున్నాయి.

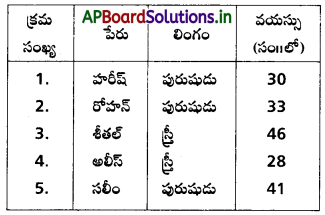
పై సమూహం నుంచి ఒక వ్యక్తిని యాధృచ్ఛికంగా ప్రసంగ కర్తగా ఎన్నుకొంటే, ఆ వ్యక్తి పురుషుడు లేదా 35 సంవత్సరాలు పైబడినవాడు అయ్యే సంభావ్యతను కనుక్కోండి.
సాధన:
5 గురు వ్యక్తులు గల పాలకవర్గం నుంచి యాదృచ్ఛికంగా ఒక వ్యక్తిని ఎన్నుకొంటే, ఎన్నుకొనే వ్యక్తి పురుషుడు అయ్యే ఘటనను A అని, మరియు 35 సంవత్సరములు దాటిన వ్యక్తి అయ్యే ఘటనను B అని మరియు శింపుల్ ఆవరణం S అనుకొనుము.
∴ n(S) = ⁵C₁ = 5
n(A) = ³C₁ = 3
P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{3}{5}\)
n(B) = ²C₁ = 2
P(B) = \(\frac{n(B)}{n(S)}\) = \(\frac{2}{5}\)
n(A ∩ B) = ¹C₁ = 1
P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}\) = \(\frac{1}{5}\)
సంభావ్యతపై సంకలన సిద్ధాంతంననుసరించి
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{3}{5}+\frac{2}{5}-\frac{1}{5}\)
= \(\frac{4}{5}\)

ప్రశ్న 13.
వందమందీ విద్యార్థుల నుంచి 40 మరియు 60 మంది విద్యార్ధులు గల రెండు సెక్షన్లు ఏర్పడ్డాయి. నీవు, నీ మిత్రుడు ఆవందమందిలో ఉండి
(i) మీ ఇద్దరూ ఒకే సెక్షన్లోకి ప్రవేశించే
(ii) వేర్వేరు సెక్షన్లలోకి ప్రవేశించే సంభావ్యతలను కనుక్కోండి.
సాధన:
S శాంపుల్ ఆవరణం అనుకొనుము.
n(S) = 100 మంది
విద్యార్థులను 40 మరియు 60 మంది విద్యార్థులుగా రెండు సెక్షన్లుగా గల విధానాల సంఖ్య = \(\frac{100 !}{40 ! 60 !}\)
(i) మీ ఇద్దరు ఒకే సెక్షన్లో ప్రవేశించే ముందుగా మీ ఇద్దరు మొదటి సెక్షన్లోకి ప్రవేశించగా మిగిలిన 98 మంది విద్యార్ధులను 38, 60 గా విభజించగల విధానాల సంఖ్య = \(\frac{98 !}{38 ! 60 !}\)
ఇదే విధంగా మీ ఇద్దరు రెండవ సెక్షన్లోకి ప్రవేశించగా మిగిలిన 98 మంది విద్యార్థులను 40, 58 గా విభజించగల విధానాల సంఖ్య

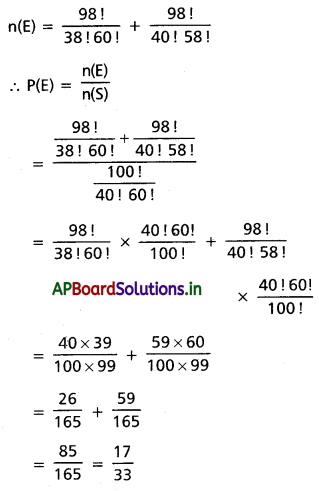
(ii) వేర్వేరు సెక్షన్లోకి ప్రవేశించే
∴ వేర్వేరు సెక్షన్లలోకి ప్రవేశించే సంభావ్యత = 1 – P(E)
= 1 – \(\frac{17}{33}\)
= \(\frac{16}{33}\)