These AP 10th Class Maths Chapter Wise Important Questions 6th Lesson శ్రేఢులు will help students prepare well for the exams.
AP Board 10th Class Maths 6th Lesson Important Questions and Answers శ్రేఢులు
ప్రశ్న 1.
– 25 అనునది 5, 3, 1, …… శ్రేణిలోని పదమేనా ? పరిశీలించండి. B
సాధన.
ఇచ్చట 5, 3, 1, …… అనునది ఒక A. P. (అంకశ్రేణి)
దీనియందు a = 5, d = a2 – a1 = 3 – 5 = – 2
పై శ్రేఢి యందు – 25 అనునది n వ పదం అనుకుందాం.
∴ an = a + (n – 1)d నందు a, d, an విలువలు ప్రతిక్షేపించగా
– 25 = 5 + (n – 1)(- 2)
– 25 = 5 – 2n + 2
– 25 – 5 – 2 = – 2n
– 32 = – 2n
⇒ n = 16 అనగా పై శ్రేణిలో – 25 అనునది 16 వ పదంగా ఉండును.
![]()
ప్రశ్న 2.
2, 2√2, 4, ….. గుణశ్రేణిలో సామాన్య నిష్పత్తిని కనుగొనుము.
సాధన.
ఇచ్చిన గుణశ్రేణి = 2, 2√2, 4, ……
సామాన్య నిష్పత్తి (r) = రెండవ పదం / మొదటి పదం
= \(\frac{2 \sqrt{2}}{2}\) = √2
∴ ఇచ్చిన శ్రేఢియందు సామాన్య నిష్పత్తి (r) = √2
ప్రశ్న 3.
1 మరియు 100 మధ్య గల 3 యొక్క గుణిజాల మొత్తం 1683 అని చూపుము.
సాధన.
1 మరియు 100 మధ్యగల 3 యొక్క గుణిజాలు = 3, 6, 9, 12, ….. 99 అనునది ఒక A.P.
దీని యందు a = 3,
సామాన్య భేదం (d) = 6 – 3 = 3
మరియు n వ పదం = 99 అనుకుందాం.
∴ an = a + (n – 1) d = 99 నందు
a = 3; d = 3 ప్రతిక్షేపించగా
= 3 + (n – 1) (3) = 99
⇒ (n – 1) (3) = 99 – 3 = 96.
∴ (n – 1) = \(\frac{96}{3}\) = 32
∴ n = 32 + 1 = 33
∴ 1 మరియు 100 ల మధ్య 3 యొక్క గుణిజాలు 33 కలవు.
∴ 3, 6, 9, 12, …… 99 ల మొత్తము = Sn = \(\frac{n}{2}\) (a + l)
= \(\frac{33}{2}\) (3 + 99)
= \(\frac{33 \times 102}{2}\)
= 33 × 51 = 1683
∴ 1 మరియు 100 ల మధ్య గల 3 యొక్క గుణిజాల మొత్తం = 1683.
![]()
ప్రశ్న 4.
117, 104, 91, 78, ……. అంకశ్రేణి యొక్క 8వ పదము కనుగొనుము.
సాధన.
ఇచ్చిన అంకశ్రేణిలో a1 = 117, a2 = 104
సామాన్య భేదము d = a2 – a1
= 104 – 117 = – 13
8వ పదము t8 = a1 + 7d
= 117 + 7(- 13)
= 117 – 91 = 26
ప్రశ్న 5.
(x – y), (x + y), (x + 3y), ………… అంకశ్రేణిలో సామాన్యభేదం ఎంత ?
సాధన.
అంకశ్రేఢి = (x-y), (x + y), (x + 3y)
సామాన్యభేదం = వరుసపదాల భేదం
= (x + y) – (x + y)
= x + y – x + y = 2y
∴ అంకశ్రేణి సామాన్యభేదం = 2y.
![]()
ప్రశ్న 6.
\(\frac{1}{4}, \frac{1}{16}, \frac{1}{64}, \frac{1}{256}\), ……………. పదాలు గుణశ్రేణిలో వున్నాయని ఏ విధంగా సమర్థిస్తారు ?
సాధన.
\(\frac{1}{4}, \frac{1}{16}, \frac{1}{64}, \frac{1}{256}\),, ………….. లోని పదాలన్నీ శూన్యేతరాలు
\(\frac{a_{2}}{a_{1}}=\frac{1}{16} \div \frac{1}{4}=\frac{1}{4}\)
\(\frac{\mathrm{a}_{3}}{\mathrm{a}_{2}}=\frac{1}{64} \div \frac{1}{16}=\frac{1}{4}\)
అన్ని సందరాలలో \(\frac{a_{n}}{a_{n-1}}=\frac{1}{4}\) కావున ఇది గుణ శ్రేణి అవుతుంది.
ప్రశ్న 7.
an అనేది అంకశ్రేణిలో n వ పదం. a1 + a2 + a3 = 102 మరియు a1 = 15 అయినa ను కనుగొనుము ?
సాధన.
a1 + a2+ a3 = 102, a = 15
= (a) + (a + d) + (a + 2d) = 102
= 3a + 3d = 102
3(15) + 3d = 102
3d = 102 – 45 = 57
d = \(\frac{57}{3}\) = 19
∴ 10వ పదం a10 = a + 9d
= 15 + 9(19)
= 15 + 171 = 186.
![]()
ప్రశ్న 8.
3 చే భాగించబడే మూడంకెల సంఖ్యలు ఎన్ని ?
సాధన.
3 చే భాగించబడే మూడంకెల సంఖ్యల జాబితా : 102, 105, 108, ……. 999
ఇది ఒక అంకశ్రేణి, ఇక్కడ a = 102, d = 3 మరియు an = 999.
an = a + (n – 1) d = 999
⇒ 102 + (n – 1) 3 = 999
⇒ 102 + 3n – 3 = 999
⇒ 3n + 99 = 999
⇒ 3n = 999 – 99 = 900
900 – 300
∴ n = 3
∴ 3 చే భాగించబడే మూడంకెల సంఖ్యలు 300 కలవు.
![]()
ప్రశ్న 9.
అంకశ్రేణిలోని మొదటి పదము 10 మరియు మొదటి 15 పదాల మొత్తం 675 అయిన అందులో 25వ పదము కనుగొనండి.
సాధన.
అంకశ్రేణిలో మొదటి పదము a = 10
సామాన్య భేదము = d అనుకొనుము
మొదటి 15 పదాల మొత్తం S15 = 675
∴ \(\frac{15}{2}\) [2a + 14d] = 675
⇒ [2 × 10 + 144] =\(\frac{675 \times 2}{15}\) = 90
⇒ 14d = 90 – 20 = 70
⇒ d = \(\frac{70}{14}\) = 5
d = 5
25వ పదము a25 = a + 24d
= 10 + 24 × 5
= 10 + 120 = 130.
![]()
ప్రశ్న 10.
ఒక గుణశ్రేణి యొక్క మొదటి పదము 50 మరియు 4వ పదము 1350 అయిన 5వ పదము ఎంత ?
సాధన.
గుణశ్రేణిలో మొదటి పదం ‘a’, సామాన్య నిష్పత్తి ‘r’ అనుకొనుము.
t1 = a = 50 అని ఇవ్వబడింది.
4వ పదం t4 = ar3 = 1350
⇒ 50.r3 = 1350
⇒ r3 = \(\frac{1350}{50}\) = 27
∴ r = 3
5వ పదం t5 = ar4
= 50(3)4 = 50 (81) = 4050.
![]()
ప్రశ్న 11.
-4, – 8, – 16, …. అనే గుణశ్రేణికి – 256 చెందునో, లేదో సరిచూడండి.
సాధన.
గుణశ్రేణి = – 4, – 8, – 16, ………………
∴ a = – 4, r = \(\frac{-8}{-4}\) = 2
∴ tn = arn – 1 = – 256
⇒ – 4 (2)n – 1 = – 256
⇒ 2n – 1 = \(\frac{-256}{-4}\) = 64
⇒ 2n – 1 = 64 = 26
⇒ n – 1 = 6.
⇒ n = 6 + 1 = 7
∴ దత్తగుణ శ్రేణిలో 7వ పదము – 256 అవుతుంది.
![]()
ప్రశ్న 12.
ఒక అంకశ్రేణిలోని మొదటి 7 పదాల మొత్తము, మొదటి 15 పదాల మొత్తము వరుపగా 98 మరియు 390 అయిన మొదటి 10 పదముల మొత్తమును కనుగొనండి.
సాధన.
AP లో మొదటి 7 పదాల మొత్తం = 98
\(\frac{7}{2}\)[22 + (7 – 1)d] = 98
2a + 6d = 98 × \(\frac{2}{7}\)
2a + 6d = 28
a + 3d = 14 …………..(1)
AP లో మొదటి 15 పదాల మొత్తం = 390
\(\frac{15}{2}\) [2a + (15 – 1)d] = 390
2a + 14d = 390 × \(\frac{2}{15}\)
2a + 14d = 52
a + 7d = 26 …………(2)
(1), (2) ల సాధించగా, a = 5 మరియు d = 3
∴ AP లో మొదటి 10 పదాల మొత్తం = \(\frac{10}{2}\) [2a + (10 – 1)d]
= 5[2(5) + 9(3)]
= 5[10 +27]
= 5 × 37 = 185.
![]()
ప్రశ్న 13.
22, 15, 8, 1, ….. అంకశ్రేణిలో – 321 ఒక పదంగా వుంటుందో లేదో పరిశీలించండి.
సాధన.
22, 15, 8, 1, ………. అను అంకశ్రేణిలో a = 22, d = – 7
అంకశ్రేణిలో 1వ పదం = an = a + (n- 1)d
ఈ అంకశ్రేణిలో 1వ పదం = – 321 అనుకొనుము.
⇒ a + (n – 1)d = – 321
⇒ 22 + (n- 1) (- 7) = – 321
⇒ (n – 1) (- 7) = – 343
⇒ n – 1 = – 343 = 49
⇒ n = 49 + 1 = 50 అనగా ఇవ్వబడిన అంకశ్రేణిలో – 321 అనేది 50వ పదముగా ఉంటుంది.
![]()
ప్రశ్న 14.
ఒక వ్యక్తి 10 సంవత్సరములలో పొదుపు చేసిన సొమ్ము ₹ 16,500 ప్రతి సంవత్సరము అతను చేయు పొదుపు సొమ్మును గత సంవత్సరం కంటే ₹ 100 పెంచుతూ పోయిన, అతను మొదటి సంవత్సరములో చేసిన పొదుపు సొమ్ము ఎంత ?
సాధన.
దత్తాంశం ప్రకారం S10 = ₹ 16,500; d = ₹ 100; n = 10; a = ?
Sn = \(\frac{n}{2}\) [2a + (n – 1)d]
16,500 = \(\frac{10}{2}\) [2a + (10 – 1) 100]
16,500 = 5(2a + 900)
\(\frac{16500}{5}\) =2a + 900
3300 = 2a + 900
2a + 900 = 3300
2a = 2400
a = \(\frac{2400}{2}\) = 1200
అతను మొదటి సంవత్సరములో చేసిన పొదుపు = ₹ 1200.
![]()
ప్రశ్న 15.
ఒక అంకశ్రేణిలో 21 పదాలు కలవు. దానిలో 10, 11, 12వ పదాల మొత్తం 129. చివరి మూడు పదాల మొత్తం 237 అయిన ఆ అంకశ్రేణిని కనుగొనండి.
సాధన.
(a + 9d) + (a + 10d) + (a + 11d) = 129
3a + 300 = 129
a + 10d = 43 …….. (1)
(a + 18d) + (a + 19d) + (a + 20d) = 237
3a + 574 = 237
a + 19d = 79 ……… (2)
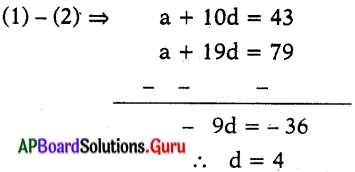
∴ d = 4
‘d’ విలువను సమీకరణం (1) లో ప్రతిక్షేపించగా,
a + 10(4) = 43
a = 43 – 40 = 3
∴ a = 3 5
∴ కావలసిన అంకశ్రేణి 3, 7, 11, 15, 19, ……