AP 10th Class Maths Important Questions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత

These AP 10th Class Maths Chapter Wise Important Questions 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత will help students prepare well for the exams.

AP Board 10th Class Maths 4th Lesson Important Questions and Answers రెండు చరరాశులలో రేఖీయ సమీకరణాల జత

ప్రశ్న 1.
x + 2y-3 = 0 మరియు 5x + ky + 7 = 0 సమీకరణాల .వ్యవస్థకు సాధన లేకుంటే ఓ విలువ కనుగొనుము.
సాధన.
x + 2y – 3 = 0
5x + ky + 7 = 0
a₁ = 1, b₁ = 2, c₁ – 3
a₂ = 5, b₂ = k, c₂ = 7
ఇచ్చిన సమీకరణాల జతకు సాధన లేకపోతే
\(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \Rightarrow \frac{1}{5}=\frac{2}{\mathrm{k}}\)
∴ k = 10
k = 10 అయినప్పుడు ఇచ్చిన పై సమీకరణాల వ్యవసకు సాధన ఉండదు.

ప్రశ్న 2.
2x + ky + 3 = 0, 4x + 6x – 5 = 0 సమీకరణాల జతకు, k యొక్క ఏ విలువకు అవి సమాంతర రేఖలు అవుతాయో కనుగొనండి.
సాధన.
ఇచ్చిన సమీకరణాల నుండి
a₁ = 2 b₁ = k c₁ = 3
a₂ = 4 b₂ = 6 c₂ = – 5
ఇచ్చిన సమీకరణాలు సమాంతర రేఖలు అయిన \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
కావున \(\frac{2}{4}=\frac{k}{6}\)
∴ k = 3

ప్రశ్న 3.
2x – ky + 3 = 0, 4x + 6y-5 = 0 సమీకరణాల జత ‘k’ యొక్క ఏ విలువకు సమాంతర రేఖలను సూచిస్తుందో కనుగొనండి.
సాధన.
ఇచ్చిన సమీకరణాల నుండి ,
a₁ = 2 b₁ = – k c₁ = 3
a₂ = 4 b₂ = 6 c₂ = – 5
ఇచ్చిన సమీకరణాలు సమాంతర రేఖలు అయిన \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
కావున, \(\frac{2}{4}=\frac{-k}{6} \neq \frac{3}{-5}\)
⇒ – 4k = 12
∴ k = – 3.

ప్రశ్న 4.
\(\) = 13 మరియు \(\) = – 2 (x ≠ 0, y ≠ 0) అనే సమీకరణాల వ్యవస్థను a, b చరరాశులతో కూడిన రేఖీయ సమీకరణాల జతగా మార్చండి.
సాధన.
సమీకరణాల వ్యవస్థ \(\frac{2}{x}+\frac{3}{y}\) = 13 …………. (1)
\(\frac{5}{x}+\frac{4}{y}\) = – 2 …………….(2)
\(\frac{1}{x}\) = a, \(\frac{1}{y}\) = b అనుకొనుము.
∴ a, b చరరాశులతో కూడిన రేఖీయ సమీకరణాల జత = 2a + 3b = 13 మరియు
5a + 4b = – 2

ప్రశ్న 5.
గ్రాఫ్ లో చూపిన సరళరేఖ యొక్క సమీకరణాన్ని రాయుము.
సాధన.

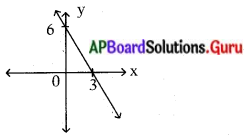
సరళరేఖా సమీకరణం = \(\frac{x}{a}+\frac{y}{b}\) = 1
\(\frac{x}{3}+\frac{y}{6}\) = 1
⇒ \(\frac{2 x+y}{6}\) = 1
⇒ 2x + y = 6.

ప్రశ్న 6.
2x – 7y = 3; 4x + y = 21 రేఖీయ సమీకరణాల జతను ప్రతిక్షేపణ పద్దతిలో సాధించండి.
సాధన.
దత్త సమీకరణాలు
2x – 7y = 3 ………….(1)
4x + y = 21 …………..(2)
రెండవ సమీకరణం నుండి y = 21 – 4x ను సమీకరణం (1) నందు ప్రతిక్షేపించగా
2x – 7(21 – 4x) = 3
⇒ 2x – 147 + 28 x = 3
⇒ 2x + 28x = 3 + 147
⇒ 30 x = 150
∴ x = \(\frac{150}{30}\) = 5
x = 5 ను y = 21 – 4x నందు ప్రతిక్షేపించగా
y = 21 – 4(5) = 21 – 20 = 1
∴ దత్త సమీకరణాల సాధన x = 5; y = 1.

ప్రశ్న 7.
10వ తరగతి చదివే 10 మంది విద్యార్థులు ఒక గణిత క్విజ్ లో పాల్గొన్నారు. దానిలో పాల్గొన్న బాలికల సంఖ్య, బాలుర సంఖ్య కన్నా 4 ఎక్కువ అయిన ఆ క్విజ్ లో పాల్గొన్న బాలుర, బాలికల సంఖ్యను కనుగొనుము.
సాధన.
బాలికల సంఖ్య = x అనుకొనుము
బాలుర సంఖ్య = y అనుకొనుము.
∴ మొత్తం విద్యార్థుల సంఖ్య x + y = 10 ………….. (1)
మరియు బాలికల సంఖ్య = బాలుర సంఖ్య + 4
x = y + 4 ……………. (2)
x = y + 4 ను సమీకరణం (1) నందు ప్రతిక్షేపించగా,
y + 4 + y = 10
⇒ 2y + 4 = 10
⇒ 2y = 10 – 4 = 6
∴ y = 3 మరియు x = 3 + 4 = 7
అనగా బాలురు 7 గురు బాలికలు ముగ్గురు పాల్గొన్నారు.

ప్రశ్న 8.
3x – y = 40, 4x – 2y = 50 సమీకరణాల జత సంగతమా ? అసంగతమా ? ఎందుకు ?
సాధన.
ఇవ్వబడిన సమీకరణాలు సంగతము.
కారణం : ఇచ్చిన సమీకరణాలు
3x – y = 40,
4x – 2y = 50
\(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{3}{4} ; \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{1}{2} ; \frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}\)
కావున, ఇచ్చిన సమీకరణాలు సంగతము.

ప్రశ్న 9.
(గాఫేతర పద్ధతిలో x + 2y = 5 మరియు 2x – y = 0 లను సాధించుము.
సాధన.
x + 2y = 5 ……. (1)
2x – y = 0 ……. (2)
2x = y
⇒ x = \(\frac{y}{2}\)
‘x’ విలువను సమీకరణం (1)లో ప్రతిక్షేపించగా
\(\frac{y}{2}\) + 2y = 5
⇒ y + 4y = 10
⇒ 5y = 10
⇒ y = 2
‘y’ విలువను సమీకరణం (2)లో ప్రతిక్షేపించగా
2x – 2 = 0
⇒ 2x = 2
⇒ x = 1
∴ x = 1, y = 2.

ప్రశ్న 10.
పరస్పరాధార సమీకరణ వ్యవస్థ ఎల్లప్పుడూ సంగతమే”. ఇది సత్యమా? అసత్యమా? సమర్థించండి.
సాధన.
పరస్పరాధారిత రేఖీయ సమీకరణాల జత ఎల్లప్పుడూ సంగత జత అవుతుంది. పరస్పరాధారిత జత సాధనలను కలిగి ఉంటుంది. కావున సంగత జత అవుతుంది.
ఎందుకనగా \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

ప్రశ్న 11.
x = 2 అనే రేఖీయ సమీకరణానికి చిత్తు పటం (గ్రాఫ్) గీయండి.
సాధన.
x = 2 యొక్క రేఖీయ సమీకరణము చిత్తు పటము

ప్రశ్న 12.
వంశీ 9 కి.గ్రా. ఉల్లిపాయలు మరియు 2 కి.గ్రా. బంగాళాదుంపలను రూ. 247 కు కొన్నాడు. బంగాళా దుంపల కంటే ఉల్లిపాయల ఖరీదు 1 కి.గ్రా.కు రూ. 3 ఎక్కువ అయితే, ప్రతి కిలోకు వాటి ధరను కనుగొనుము.
సాధన.
1 కి.గ్రా. బంగాళాదుంపల ఖరీదు x. .
అయితే 1 కి.గ్రా. ఉల్లిపాయల ఖరీదు x + 3
x + x + 3 = 247
2x + 3 = 247
⇒ 2x = 244
⇒ x = \(\frac{244}{2}\) = రూ. 122.
1 కి.గ్రా. బంగాళాదుంపల ఖరీదు = రూ. 122
1 కి.గ్రా. ఉల్లిపాయల ఖరీదు = x + 3
= 122 + 3 = రూ. 125.

ప్రశ్న 13.
2x + y – 5 = 0, 3x – 2y – 4 = 0 లను చరరాశి తొలగించు పద్ధతి ద్వారా సాధించండి.
సాధన.
ఇచ్చిన సమీకరణాలతో ఏదైనా ఒక చరరాశి గుణకాలను సమానం చేయుట ద్వారా ఈ పద్ధతిన సాధిస్తాం.
దత్త సమీకరణాలు :
2x + y – 5 = 0 …………….(1)
3x – 2y – 4 = 0 ……………..(2)
సమీకరణం (1)నకు ఇరువైపులా 3 చేతను, సమీకరణం (2) నకు ఇరువైపులా 2 చేత గుణించగా

⇒ y = \(\frac{7}{7}\) = 1
∴ y = 1
y = 1 ను సమీకరణం (1) నందు ప్రతిక్షేపించగా
2x + y = 5
2x + 1 = 5
2x = 5 – 1 = 4
∴ 2x = 4
అయిన x = \(\frac{4}{2}\) = 2
∴ x = 2 .
దత్త సమీకరణాలకు సాధన : x = 2 ; y = 1

సరిచూచుట :
2x + y = 5
2(2) + 1 = 5
4 + 1 = 5
LHS = RHS

5 = 5
3x – 2y – 4 = 0
3(2) – 2(1) – 4 = 0
6 – 2 – 4 = 0
6 – 6 = 0
LHS = RHS.

ప్రశ్న 14.
క్రింది ఇవ్వబడిన సమీకరణాలను గ్రాఫ్ ద్వారా సాధించుము.
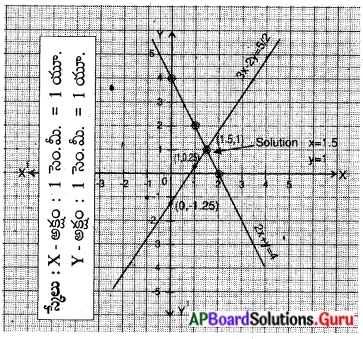
\(\frac{1}{3} x-\frac{1}{2} y\) = 1; 2x – \(\frac{1}{3}\)y = – \(\frac{2}{3}\)
సాధన.
\(\frac{1}{3} x-\frac{1}{2} y\) = 1 మరియు 2x – \(\frac{1}{3}\)y = – \(\frac{2}{3}\) ఈ సమీకరణాలను ముందుగా రేఖీయ సమీకరణ రూపం లోకి మార్చుదాం.
\(\frac{1}{3} x-\frac{1}{2} y\) = 1
⇒ \(\frac{2 x-3 y}{6}\) = 1
⇒ 2x- 3y = 6 ……………. (1) మరియు
2x – \(\frac{1}{3}\)y = – \(\frac{2}{3}\)
6x – y = – 2 ……………. (2)

(i) 2x – 3y = 6
⇒ y = \(\frac{2 x-6}{3}\)

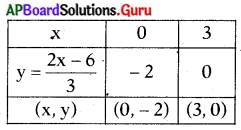
ఈ 25 – 3y = 6 రేఖ పై (0; – 2) మరియు (3, 0) బిందువులు గలవు.

(ii) 6x – y = – 2 = y
⇒ y = 6x + 2 –

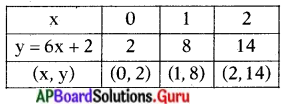
ఈ 6x – y = – 2 అను రేఖపై (0, 2) (1, 8), (2, 14) అను బిందువులు గలవు.
పై రెండు రేఖలు (0.75, 2.5) బిందువుల వద్ద ఖండించుకొనుచున్నవి. కావున
∴ సాధన x = 0.75, y = 2.5

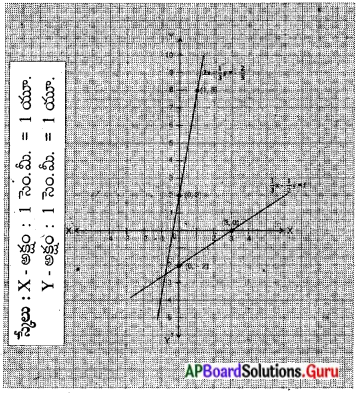
ప్రశ్న 15.
క్రింది రేఖీయ సమీకరణాల జతను గ్రాఫ్ ద్వారా సాధించండి. 2x + y = 4 మరియు 2x – 3y = 12.
సాధన.
దత్త సమీకరణాలు : –
2x + y – 4 = 0 మరియు 2x – 3y – 12 = 0
\(\frac{a_{1}}{a_{2}}=\frac{2}{2}\) = 1;\(\frac{b_{1}}{b_{2}}=\frac{1}{-3}\) మరియు \(\frac{c_{1}}{c_{2}}=\frac{-4}{-12}=\frac{1}{3}\)
∴ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
కనుక సమీకరణాలు సంగత రేఖీయ సమీకరణాలు.
∴ అవి ఒకే ఒక బిందువు వద్ద ఖండించుకొనుట వలన ఒక సాధన మాత్రమే ఉండును.

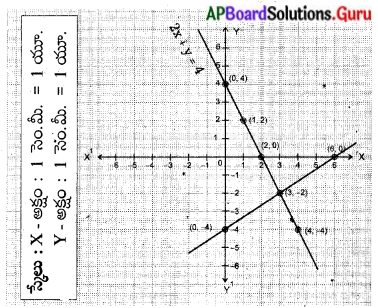
గ్రాఫు పరిశీలించగా ఇచ్చిన సమీకరణాల సాధన x = 3 మరియు y = – 2.

ప్రశ్న 16.
6 పెన్సిళ్ళు మరియు 4 నోటు పుస్తకముల మొత్తము వెల రూ. 90/-. అలాగే 8 పెన్సిళ్ళు మరియు 3 నోటు పుస్తకముల మొత్తము వెల రూ. 85/-. అయితే ప్రతీ పెన్సిల్ మరియు నోట్ పుస్తకము వెల ఎంత ?
సాధన.
ఒక పెన్సిల్ వెల = రూ. x
నోటు పుస్తకం వెల = రూ. y అనుకొనుము.
6 ‘పెన్సిల్స్, 4 నోటు పుస్తకంల మొత్తం వెల = రూ. 90
⇒ 6x + 4y = 90 …………(1)
8 పెన్సిల్స్, 3 నోటు పుస్తకంల మొత్తం వెల = రూ. 85
⇒ 8x + 3y = 85 …………..(2)
⇒ 1 × 3 = 18x + 12y = 270 ………….(3)
⇒ 2 × 4 = 32x + 12y = 340 ……….(4)

x విలువను (1)లో ప్రతిక్షేపించిన
6 × 5 + 4y = 90
4y = 90 – 30 = 60
y = \(\frac{60}{4}\) = 15
x = 5, y = 15
పెన్సిల్ వెల = రూ. 5
నోటు పుస్తకం వెల = రూ. 15.

ప్రశ్న 17.
క్రింది సమీకరణాల జతను సాధించుము. \(\frac{3}{x+y}+\frac{2}{x-y}\) = 2 మరియు \(\frac{9}{x+y}-\frac{4}{x-y}\) = 1.
సాధన.
మనకు ఇచ్చిన సమీకరణాలు
\(3\left(\frac{1}{x+y}\right)+2\left(\frac{1}{x-y}\right)\) = 2 → (1)

\(9\left(\frac{1}{x+y}\right)-4\left(\frac{1}{x-y_{k}}\right)\) = 1 → (2)

మరియు \(\frac{1}{x+y}\) = p మరియు \(\frac{1}{x-y}\) = q
ప్రతిక్షేపించగా, క్రింది రేఖీయ సమీకరణాల జత ఏర్పడుతుంది.
3p + 2q = 2 → (3)
9p – 4q = 1 → (4)

q విలువను (3) లో ప్రతిక్షేపించగా 3p + 2(\(\frac{1}{2}\)) = 2
⇒ 3p + 1 = 2
⇒ 3p = 1
∴ p = \(\frac{1}{3}\)

ప్రశ్న 18.
క్రింది సమీకరణాలను ఒక జత రేఖీయ సమీకరణాలుగా మార్చి సాధించుము.
\(\frac{5}{(x+y)}-\frac{2}{(x-y)}\) = – 1
\(\frac{15}{(x+y)}-\frac{7}{(x-y)}\) = – 10, (x ≠ 0, y ≠ 0)
సాధన.
ఇవ్వబడినవి, \(\frac{5}{(x+y)}-\frac{2}{(x-y)}\) = – 1 మరియు
\(\frac{5}{(x+y)}-\frac{2}{(x-y)}\) = – 10
\(\frac{1}{(x+y)}\) = a, \(\frac{1}{(x-y)}\) = b గా తీసుకొనుము.
ఈ సమీకరణాలు ఈ క్రింది విధంగా మారినవి.
5a – 2b = – 1 ……………….(1)
15a-7b = -10 ………………(2)

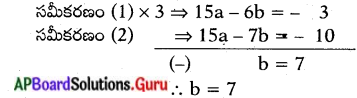
b = 7 విలువను సమీకరణం (1)లో ప్రతిక్షేపించగా
5a – 2(7) = – 1
⇒ 5a = – 1 + 14
⇒ 5a = 13
⇒ a = \(\frac{13}{5}\)

కాని a = \(\frac{1}{x+y}=\frac{13}{5}\)
⇒ x + y = \(\frac{5}{13}\)

b = \(\frac{1}{x-y}\) = 7
⇒ x – y = \(\frac{1}{7}\)
పై సమీకరణాలను సాధించంగా

x = \(\frac{24}{91}\) విలువను x + y = \(\frac{5}{13}\) లో ప్రతిక్షేపించగా .
\(\frac{24}{91}\) + y = \(\frac{5}{13}\)
⇒ y = \(\frac{5}{13}-\frac{24}{91}=\frac{35-24}{91}\)
∴ y = \(\frac{11}{91}\)
∴ సాధన (x, y) = (\(\frac{24}{91}\), \(\frac{11}{91}\))