AP 10th Class Maths Important Questions Chapter 7 రేఖాగణితం

These AP 10th Class Maths Chapter Wise Important Questions 7th Lesson రేఖాగణితం will help students prepare well for the exams.

AP Board 10th Class Maths 7th Lesson Important Questions and Answers రేఖాగణితం

ప్రశ్న 1.
(2, 0) మరియు (0, 2) బిందువులను కలుపు రేఖా
ఖండాన్ని 1 : 1 నిష్పత్తిలో విభజించే బిందువు నిరూపకా . లను కనుగొనండి.
సాధన.
x₁ = 2 ; x₂ = 0; y₁ = 0; y₂ = 2
1 : 1 నిష్పత్తిలో విభజించు బిందు నిరూపకాలు (లేదా) మధ్య బిందువు నిరూపకాలు
= \(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)\)
= \(\left(\frac{2+0}{2}, \frac{0+2}{2}\right)\)
= (1, 1).

ప్రశ్న 2.
(a cos θ, 0) మరియు (0, a sin θ) బిందువుల మధ్య దూరము కనుగొనుము.
సాధన.
(a cos θ, 0) మరియు (0, a sin θ) బిందువుల మధ్య దూరం (x₁, y₁) మరియు (x₂, y₂) బిందువుల మధ్య దూరమునకు సూత్రము :
= (x, – X2)2 + (y! – y )2 నందు
x₁ = a cos θ, y₁ = 0;
x₂ = 0, y₂ = a sin θ ప్రతిక్షేపించగా
పై బిందువుల మధ్య దూరం = \(\sqrt{(a \cos \theta-0)^{2}+(0-a \sin \theta)^{2}}\)
= \(\sqrt{\mathrm{a}^{2} \cos ^{2} \theta+\dot{\mathrm{a}}^{2} \sin ^{2} \theta}\)
= \(\sqrt{a^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)}\)
= \(\sqrt{a^{2}(1)}=\sqrt{a^{2}}\) = a
∴ వాని మధ్య దూరం = a యూనిట్లు.

ప్రశ్న 3.
A(4, 0), B(0, y) మరియు AB = 5 అయిన లకు సాధ్య విలువలు కనుక్కోండి.
సాధన.
A(4, 0); B(0 y); AB = 5 .
\(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\) = 5
\(\sqrt{16+y^{2}}\) = 5
√16 + y² = 5
16 + y² = 25
y² = 25 – 16 = 9
y = ± √9 = ± 3
yకు సాధ్యపడు విలువలు 3 లేదా – 3.

ప్రశ్న 4.
(3, 2) కేంద్రంగా ఉంటూ (4, – 1) బిందువు గుండా పోయే వృత్త వ్యాసార్థాన్ని కనుగొనుము.
సాధన.

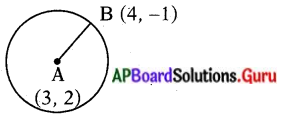
వ్యాసార్ధం = AB
బిందువుల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

వ్యాసార్థం ‘r’ = \(\sqrt{(4-3)^{2}+(-1-2)^{2}}\)

= \(\sqrt{(1)^{2}+(-3)^{2}}\)

= \(\sqrt{1+9}=\sqrt{10}\) యూ.

ప్రశ్న 5.
∆ABC త్రిభుజము యొక్క మూడు శీర్షాలు A(3, – 2), B(- 5, 4) మరియు C(2, – 2) అయిన దాని గురుత్వ కేంద్రము గురించి ఏమి పరిశీలించితివి?
సాధన.
త్రిభుజ గురుత్వ కేంద్రము
= \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)

= \(\left(\frac{3+(-5)+2}{3}, \frac{-2+4+(-2)}{3}\right)\) = (0,0)
గురుత్వ కేంద్రము మూలబిందువు అని పరిశీలించితిని.

ప్రశ్న 6.
(6, 2), (0, 0) మరియు (4, – 5) శీర్ష బిందువులుగా కల్గిన త్రిభుజ గురుత్వ కేంద్రాన్ని కనుగొనండి.
సాధన.

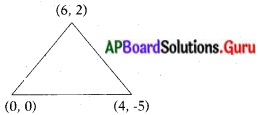
త్రిభుజ శీర్షబిందువులు = (6, 2) (0, 0) మరియు (4, – 5)
గురుత్వ కేంద్రము = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)

= \(\left(\frac{6+0+4}{3}, \frac{2+0-5}{3}\right)\)

= \(\left(\frac{10}{3}, \frac{-3}{3}\right)=\left(\frac{10}{3},-1\right)\)

ప్రశ్న 7.
(3, 2) బిందువు కేంద్రంగా (-5, 6) బిందువు గుండా పోయే వృత్తవ్యాసార్ధమును కనుగొనండి.
సాధన.
దత్తాంశం ప్రకారం, వృత్తం A (3, 2) బిందువు కేంద్రంగా B (- 5, 6) బిందువు గుండా పోతుంది.

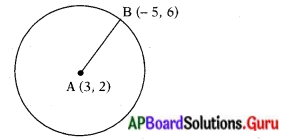
వ్యాసార్ధం = AB [∵ వృత్త కేంద్రం నుండి బిందువుకు గల దూరం]
దూరం = \(\sqrt{\left(\mathrm{x}_{2} \cdot-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
వ్యాసార్ధం ‘r’ = \(\sqrt{(-5-3)^{2}+(6-2)^{2}}\)
= √64 + 16 = √80
= √16 x 5 = 4√5 యూ.

ప్రశ్న 8.
(0, – sin x) మరియు (- cos x, 0) ల మధ్య దూరం కనుగొనండి.
సాధన.
(0, – sin x) మరియు (- cos x, 0) ల మధ్య దూరం
= \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
= \(\sqrt{(-\cos x-0)^{2}+(0+\sin x)^{2}}\)
= \(\sqrt{\cos ^{2} x+\sin ^{2} x}\) = √1 = 1 యూ.

ప్రశ్న 9.
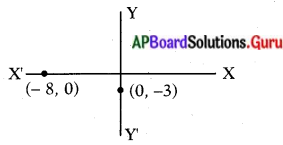
బిందువులు (0, – 3) మరియు (-8, 0) లు నిరూపక తలంలో ఎక్కడ ఉంటాయో తెల్పండి.
సాధన.
(0, – 3) బిందువు నందు X నిరూపకం = 0 కావున ఈ బిందువు Y – అక్షంపై ఉండును. మరియు ఈ బిందువు యొక్క Y నిరూపకం – 3 అనగా ఋణాత్మకం కావున OY పై ఉంటుంది. అదే విధంగా బిందువు (- 8, 0) నందు Y నిరూపకం విలువ ‘O’ కావున ఇది X – అక్షంపై ఉండును. మరియు దీనియొక్క X నిరూపకం – 8 అనగా ఋణాత్మకం కావున OX పై ఉంటుంది.

ప్రశ్న 10.
(7, 2), (5, 1) మరియు (3, k) బిందువులు సరేఖీయాలైతే k విలువెంత ?
సాధన.
బిందువులు సరేఖీయాలైన ఆ బిందువులతో ఏర్పడు
త్రిభుజ వైశాల్యం = 0
త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) |7(1 – k) + 5(k – 2) + 3(2 – 1)|
= \(\frac{1}{2}\) | – 2k| = 0
∴ k = 0

ప్రశ్న 11.
(- 4, 4), (- 2, 2) మరియు (6, – 6) బిందువులను శీర్షములుగా కలిగిన త్రిభుజ గురుత్వ కేంద్రమును కనుక్కోండి.
సాధన.
త్రిభుజ గురుత్వ కేంద్రము
= \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
= \(\)= (0, 0).

ప్రశ్న 12.
బిందువులు (x, 1) మరియు (- 1, 5) ల మధ్య దూరము ‘5’ యూనిట్లు అయిన ‘x’ విలువ ఎంత ?
సాధన.
రెండు బిందువుల మధ్య దూరం = \(\sqrt{\left(\mathrm{x}_{1}-\mathrm{x}_{2}\right)^{2}+\left(\mathrm{y}_{1}-\mathrm{y}_{2}\right)^{2}}\)
(x, 1), (- 1, 5) బిందువుల మధ్య దూరం = 5
\(\sqrt{[x-(-1)]^{2}+(1-5)^{2}}\) = 5
\(\sqrt{(x+1)^{2}+(-4)^{2}}\) = 5
x² + 1 + 2x + 16 = 25
x² + 2x – 8 = 0
(x + 4) (x – 2) = 0
x = – 4 లేదా x = 2.

ప్రశ్న 13.
5 సెం.మీ., 12 సెం.మీ., 13 సెం.మీ. భుజములుగా గల త్రిభుజ వైశాల్యమును హెరాన్ సూత్రము ద్వారా, కనుగొనుము.
సాధన.
a = 5 సెం.మీ., b = 12 సెం.మీ., c = 13 సెం.మీ. అనుకొనుము
s = \(\frac{a+b+c}{2}=\frac{5+12+13}{2}\) = 15
త్రిభుజ వైశాల్యం (∆) (∆) = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15(15-5)(15-12)(15-13)}\)
= 30 సెం.మీ.²

ప్రశ్న 14.
గ్రాఫ్ ను పరిశీలించి, క్రింది ప్రశ్నలకు జవాబులివ్వండి.

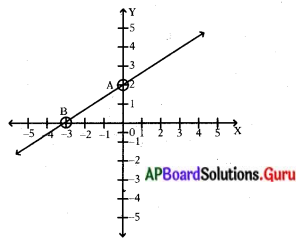
(i) A మరియు B బిందువుల నిరూపకాలు రాయండి.
(ii) \(\overrightarrow{\mathbf{A B}}\) సరళరేఖ యొక్క వాలు కనుగొనండి.
సాధన.
(i) ‘A’ బిందు నిరూపకము = (0, 2)
‘B’ బిందు నిరూపకము = (- 3, 0)

(ii) వాలు = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{0-2}{-3-0}=\frac{-2}{-3}=\frac{2}{3}\)

ప్రశ్న 15.
(1, 5), (2, 5) మరియు (-2, – 1) బిందువులు సరేఖీయాలు అగునో, కావో కనుగొనండి.
సాధన.
A(1, 5), B(2, 5), C(- 2, – 1)
మధ్య దూరం = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
AB = \(\sqrt{(2-1)^{2}+(5-5)^{2}}\)
= \(\sqrt{1+0}\) = 1

BC = \(\sqrt{(-2-2)^{2}+(-1-5)^{2}}\)
= \(\sqrt{16+36}=\sqrt{52}=2 \sqrt{13}\)

CA = \(\sqrt{(1+2)^{2}+(5+1)^{2}}\)
= \(\sqrt{9+36}=\sqrt{45}=3 \sqrt{5}\)

ప్రశ్న 16.
AB ఒక వృత్త వ్యాసము. కేంద్రము (2, -3) మరియు B (1, 4) అయితే, A నిరూపకాలు కనుక్కోండి.
సాధన.

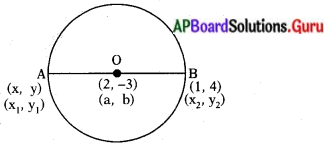
మదబిందువు = \(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\)
\(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}\) = a… (1)
\(\frac{x+1}{2}\) = 2
x + 1 = 4
x = 4 – 1 = 3
x = 3

\(\frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\) = b …………. (2)
\(\frac{y+4}{2}\) = – 3
y + 4 = – 6
y = – 10
∴ A = 3, – 10.

ప్రశ్న 17.
ఈ క్రింద ఇవ్వబడిన బిందువులు సరేఖీయాలు అవుతాయా ? కాదా ? సరిచూడండి. (1, – 1), (4, 1), (- 2, -3 )
సాధన.
త్రిభుజం యొక్క వైశాల్యం ‘సున్న అయితే ఇవ్వబడిన మూడు బిందువులు సరేఖీయాలు అవుతాయి. ఇవ్వబడిన బిందువులు (1, – 1), (4, 1), (- 2, – 3)
త్రిభుజం యొక్క వైశాల్యం ∆ = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|
= \(\frac{1}{2}\) |1(1 + 3) + 4(- 3 + 1) – 2 (-1 – 1)|
= \(\frac{1}{2}\) |4 – 8 + 4|
= \(\frac{1}{2}\) |8 – 8|
= \(\frac{1}{2}\) |0| = 0
కావున, మూడు బిందువులు సరేఖీయాలు.

ప్రశ్న 18.
(3, 0), (6, 4) మరియు (-1, 3) బిందువులు లంబకోణ సమద్విబాహు త్రిభుజ శీర్షాలు అవుతాయో లేదో సరి చూడండి. త్రిభుజ వైశాల్యం కూడా కనుగొనుము.
సాధన.
A(3, 0), B(6, 4) బిందువుల మధ్య దూరం

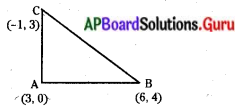
AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(6-3)^{2}+(4-0)^{2}}\)
= \(\sqrt{9+16}\) = 5 యూ.

B(6, 4), C(- 1, 3) బిందువుల మధ్య దూరం
BC = \(\sqrt{(-1-6)^{2}+(3-4)^{2}}\)
= \(\sqrt{(-7)^{2}+(-1)^{2}}=\sqrt{50}\) యూ.

C(- 1, 3), A(3, 0) బిందువుల మధ్య దూరం
CA = \(\sqrt{[3-(-1)]^{2}+(0-3)^{2}}\)
= \(\sqrt{16+9}\) = 5 యూ.
∴ AB² = 25, BC² = 50, CA² = 25,
BC² = AB² + CA² మరియు AB = CA
∴ ∆ ABC లంబకోణ సమద్విబాహు, త్రిభుజం అవుతుంది.
∴ ∆ ABC వైశాల్యం = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × 5 × 5 = 12.5 చ. యూ.

ప్రశ్న 19.
(2, 3), (- 1, 3) మరియు (2, – 1) బిందువులచే ఏర్పడు త్రిభుజ వైశాల్యమును హెరాన్ సూత్రమును ఉపయోగించి కనుగొనుము.
సాధన.
(2, 3) (- 1, 3) మరియు (2, – 1) బిందువులచే ఏర్పడు త్రిభుజ వైశాల్యంను హెరాన్ సూత్రంను ఉపయోగించి కనుగొనుట.
పటంలో చూపినట్లు ∆ABC యొక్క శీర్షాల నిరూపకాలు A(2, 3) ; B(- 1, 3) మరియు C(2, – 1) అనుకుందాం.

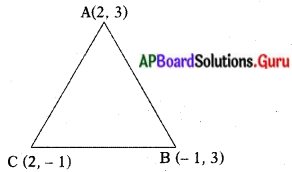
∴ ఆ త్రిభుజ భుజాల పొడవులు AB = c, BC = a, CA = b తో సూచిస్తాం.
హెరాన్ సూత్ర పద్ధతిన త్రిభుజ వైశాల్యము = \(\sqrt{s(s-a)(s-b)(s-c)}\)
ఇక్కడ s = \(\frac{a+b+c}{2}\) కావున మనం భుజాల పొడవులు కనుగొందాం.

భుజాల పొడవులను \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) సూత్ర సహాయాన కనుగొందాం.
∴ AB = c = (2, 3) మరియు (- 1, 3) బిందువుల మధ్య దూరం.
c = \(\sqrt{(2-(-1))^{2}+(3-3)^{2}}\)
= \(\sqrt{(2+1)^{2}+0^{2}}\)
= \(\sqrt{3^{2}+0}=\sqrt{3^{2}}\) = 3

మరియు BC = a = (- 1, 3) మరియు (2, – 1) ల మధ్య దూరం
a = \(\sqrt{(-1-2)^{2}+[3-(-1)]^{2}}\)
= \(\sqrt{(-3)^{2}+(3+1)^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5

మరియు CA = b = (2, – 1) మరియు (2, 3) బిందువుల మధ్య దూరం b = \(\sqrt{(2-2)^{2}+(-1-3)^{2}}\)
= \(\sqrt{0^{2}+4^{2}}=\sqrt{16}\) = 4
∴ a = 5, b = 4, c = 3
⇒ s = \(\frac{a+b+c}{2}=\frac{5+4+3}{2}=\frac{12}{2}\) = 6
∴ ∆ABC వైశాల్యము = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{6(6-5)(6-4)(6-3)}\)
= \(\sqrt{6(1)(2)(3)}=\sqrt{6 \times 6}\) = 6 చ||యూ.
∴ ఇచ్చిన త్రిభుజ వైశాల్యము = 6 చ||యూ.

ప్రశ్న 20.
బిందువులు A(6, 1), B (8, 2), C(9, 4) మరియు D(p, 3) లు వరుసగా సమాంతర చతుర్భుజ శీర్యాలయిన,
(i) p యొక్క విలువను కనుగొనుము.
(ii) ▱ ABCD వైశాల్యమును కనుగొనుము.
సాధన.
(i) A, B, C, D లు సమాంతర చతుర్భుజ శీర్షాలు
కావున AC మధ్య బిందువు = BD మధ్య బిందువు

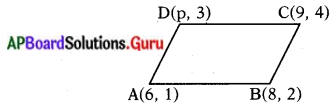
A(6, 1) = (x₁, y₁); C(9, 4) = (x₂, y₂)
AC మధ్య బిందువు = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
= \(\left(\frac{6+9}{2}, \frac{1+4}{2}\right)\)
= \(\left(\frac{15}{2}, \frac{5}{2}\right)\)

B(8, 2) = (x₁, y₁); D(p, 3) = (x₂, y₂)
BD మధ్య బిందువు = \(\left(\frac{8+p}{2}, \frac{2+3}{2}\right)\)
= \(\left(\frac{8+p}{2}, \frac{5}{2}\right)\)
∴ \(\frac{8+p}{2}=\frac{15}{2}\)
∴ p = 7.

(ii) ∆ABC వైశాల్యము = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |6(2 – 4) + 8(4 – 1) + 9(1 – 2)|
= \(\frac{1}{2}\) |- 12 + 24 – 9|
= \(\frac{1}{2}\) |3| = \(\frac{3}{2}\)
∴ సమాంతర చతుర్భుజం ABCD వైశాల్యము = 2 × ∆ABC వైశాల్యము
= 2 × \(\frac{3}{2}\) = 3 చ.యూ.

ప్రశ్న 21.
‘k’ యొక్క ఏ విలువకు బిందువులు (3k – 1, k – 2), (k, k – 7) మరియు (k – 1, – k – 2) లు సరేఖీయాలగును?
సాధన.
దత్త బిందువులు సరేఖీయాలు. . అనగా A (3k – 1, k – 2), B (k, k – 7) మరియు C (k – 1, – k – 2) బిందువులు ABC రేఖపై ఉండును.
\(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{AC}}\) ల వాలులు సమానము. (∵ అవి సరేఖీయాలు)
వాలు = y – నిరూపకాల భేదం / x – నిరూపకాల భేదం
= \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

\(\overline{\mathrm{AB}}\) వాలు = \(\frac{(\mathrm{k}-7)-(\mathrm{k}-2)}{\mathrm{k}-(3 \mathrm{k}-1)}\)
= \(\frac{k-7-k+2}{k-3 k+1}\)
= \(\frac{-5}{1-2 k}\) ………………(1)

A(3k – 1, k – 2), C(k – 1, – k – 2)
\(\overline{\mathrm{AC}}\) వాలు = \(\frac{(-k-2)-(k-2)}{(k-1)-(3 k-1)}\)
= \(\frac{-k-2-k+2}{k-1-3 k+1}\)
= \(\frac{-2 \mathrm{k}}{-2 \mathrm{k}}\) = 1
(1) = (2)
⇒ \(\frac{-5}{1-2 k}\) = 1
⇒ 1 – 2k = – 5
⇒ 1 + 5 = 2k
⇒ 2k = 6
∴ k = 3