AP State Syllabus AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 4 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 10th Lesson Algebraic Expressions Exercise 4
![]()
Question 1.
Add the following algebraic expressions using both horizontal and vertical methods. Did
you get the same answer with both methods.
(i) x2 – 2xy + 3y2; 5y2 + 3xy – 6x2
(ii) 4a2 + 5b2 + 6ab 3ab ; 6a2 – 2b2 ; 4b2 – 5ab
(iii) 2x + 9y – 7z ; 3y + z + 3x ;2x – 4y – z
(iv) 2x2 – 6x + 3 ; – 3x2 – x – 4 ; 1 + 2x – 3x2
Solution:
(i) x2 – 2xy + 3y2; 5y2 + 3xy – 6x2
Addition by Horizontal method
(x2 – 2xy + 3y2) + ( – 6x2 + 3xy + 5y2)
= (x2 – 6x2) + ( – 2xy + 3xy) + (3y2 + 5y2)
= – 5x2 + xy + 8y2 .

ii) 4a2 + 5b2 + 6ab;3ab; 6a2 – 2b2; 4a2 – 5ab
Horizontal Method
(4a2 + 5b2 + 6ab) + 3ab + (6a2 – 2b2) (4a2 – 5ab)
= (4a2 + 6a2 + 4a2) + (5b2 – 2b2) + (6ab + 3ab – 5ab)
= 14a2 + 3b2 + 4ab

![]()
iii) 2x2 + 9y – 7z ; 3y + z + 3x; 2x4y – z
Horizontal Method
= (2x + – 7z) + (3y + z + 3x) + (2x – 4y – z)
= (2x + 3x + 2x) + (9y + 3y_4y) + ( – 7z + z – z)
= 7x + 8y – 7z

iv) 2x2 – 6x – 3; – 3x2 – x – 4; 1 + 2x – 3x2
Horizontal Method
(2x2 – 6x + 3) + ( – 3x2 – x – 4) + (1 + 2x – 3x2)
(2x2 – 3x2 – 3x2) + (- 6x – x + 2x) + (3 – 4 + 1)
= – 4x2 – 5x + 0
= – 4x2 – 5x

In all the above sums
(i), (ii), (iii), (iv) we got same answer in both horizontal and vertical methods.
![]()
Question 2.
Simpli1’: 2x2 + 5x – 1 + 8x + x2 + 7 – 6x + 3 – 3x2
Solution:
Given algebraic expression is
2x2 + 5x – 1 + 8x + x2 + 7 – 6x + 3 – 3x2
= (2x2 + x2 – 3x2) + (5x + 8x – 6x) . ( – 1 + 7 + 3)
= 0 + 7x + 9 = 7x + 9
Question 3.
Find the perimeter of the following rectangle?

Solution:
The perimeter of a rectangle = 2 (length + breadth)
= 2 (6x + y + 3x – 2y)
= 2 (9x – y)
∴ P = (18x – 2y) units
Question 4.
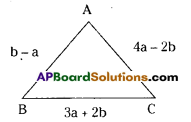
Find the perimeter of a triangle whose sides are 2a + 3b, b – a, 4a – 2b.
Solution:
Perimeter of the triangle ABC = \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CA}}\)
= (b – a) + (3a + 2b) + (4a – 2b)
=( – a + 3a + 4a) +(b + 2b – 2b)
= (6a + b) units
![]()
Question 5.
Subtract the second expression from the first expression
(i) 2a + b, a – b
(ii) x + 2y + z , – x – y – 3z
(iii) 3a2 – 8ab – 2b2, 3a2 – 4ab+6b2
(iv) 4pq – 6p2 – 2q2, 9p2
(v) 7 – 2x – 3x2, 2x2 – 5 x – 3
(vi) 5x2 – 3xy – 7y2 , 3x2 – xy – 2y2
(vii) 6m3 + 4m2 + 7m – 3 , 3m3 + 4
Solution:
(i) 2a + b, a – b = 2a + b – a + b
= (2a – a) + (b + b)
= a + 2b
ii) (x + 2y + z) – ( – x – y – 3z) = x + + z + x + y + 3z
=(x + x) + (2y + y) +(z + 3z)
= 2x + 3y + 4z
iii) (3a2 – 8ab – 2b2) – (3a2 – 4ab + 6b2) = 3a2 – 8ab – 2b2 – 3a2 +4ab – 6b2
= (3a2 – 3a2) + ( – 8ab + 4ab) + (2b2 – 6b2)
= 0 – 4ab – 8b2
= – 4ab – 8b2
iv) (4pq – 6p2 – 2q2) – (9p2) = 4pq – 6p2 – 2q2 – 9p2
= 4pq – 15p2 – 2q2
v) (7 – 2x – 3x2) – (2x2 – 5x – 3)=7 – 2x – 3x2 – 2x2 + 5x + 3
= ( – 3x2 – 2x2) + ( – 2x + 5x) + (7 + 3)
= – 5x2 + 3x + 10
![]()
vi) (5x2 – 3xy – 7y2) – (3x2 – xy – 2y2) = 5x2– 3xy – 7y2 – 3x2 + xy + 2y2
= (5x2 – 3x2) + ( – 3xy + xy) + ( – 7y2 + 2y2)
= 2x2 – 2xy – 5y2
viii) (6m3 + 4m2 + 7m – 3) – (3m3 + 4)= 6m3 + 4m2 + 7m – 3 – 3m3 – 4
= (6m3 – 3m3) + 4m2 + 7m + (- 3 – 4)
= 3m3 + 4m2 + 7m – 7
Question 6.
Subtract the sum of x2 – 5xy + 2y2 and y2 – 2xy – 3x2 from the sum of 6x2 – 8xy – y2 and 2xy – 2y2 – x2.
Solution:
The sum of x2 – 5xy + 2y2 and y2 – 2xy – 3x2 = (x2 – 5xy + 2y2) (y – 2xy – 3x2)
= (x2 – 3x2) + ( – 5xy – 2xy) + (2y2 + y2)
= – 2x2 – 7xy + 3y2 ………………….(1)
The sum of 6x2 – 8xy – y2 and
2xy – 2y2 – x2 = (6x2 – 8xy – y2) + (2xy – 2y2 – x2)
= (6x2 – x2) + ( – 8xy + 2xy) + (-y2 – 2y2)
= 5x2 – 6xy – 3y2 ………………. (2)
From (1) and (2)
(2) – (1)= (5x2 – 6xy – 3y2) – ( – 2x2 – 7xy + 3y2)
= 5x2 – 6xy – 3y2 + 2x2 + 7xy – 3y2
= (5x2 + 2x2) + ( – 6xy + 7xy) + ( – 3y2 – 3y2)
= 7x2 + xy – 6y2
![]()
Question 7.
What should be added to 1 + 2x – 3x2 to get x2 – x – 1?
Solution:
Let the added algebraic expression may be ‘A say
(1 + 2x – 3x2) + A = x2 – x – 1
=A =(x2 – x – 1) – (1 + 2x – 3x2)
= x2 – x – 1 – 1 – 2x + 3x2
= (x2 + 3x2) + ( – x – 2x) +( – 1 – 1)
∴ A = 4x2 – 3x – 2
∴ The required added expression (A) = 4x2 – 3x – 2
Question 8.
What should be taken away from 3x2 – 4y2 + 5xy +20 to get – x2 – y2 + 6xy + 20.
Solution:
Let the subtracted algebraic expression may be B’ say
3x2 – 4y2 + 5xy – B = – x2 – y2 + 6xy + 20
B = (3x2 – 4y2 + 5xy) – (- x2 – y2 + 6xy + 20)
= 3x2 – 4y2 + 5xy + x2 +y2 – 6xy – 20
= (3x2 + x2) ( – 4y2 + y2) + (5xy – 6xy) – 20
∴ B = 4x2 – 3y2 – xy – 20
∴ The required subtracted expression is B = 4x2 – 3y2 – xy – 20
![]()
Question 9.
The sum of 3 expressions is 8 + 13a + 7a2. Two of them are 2a2 + 3a + 2 and 3a2 – 4a + 1. Find the third expression.
Solution:
Given that f he sum of 3 expressions is 8 + 13a + 7a2 ……………..(1)
Two of them are 2a2 + 3a + 2 and 3a2 – 4a + 1.
∴ The sum of above two expressions (2a2 + 3a + 2) + (3a2 – 4a + 1)
= 2a2 + 3a + 2 + 3a2 – 4a + 1.
= (2a2 + 3a2) + (3a – 4a) + (2 + 1)
= 5a2 – a + 3
∴ The required 3rd expression (1) – (2)
(1) – (2) =(7a2 + 13a + 8) – (5a2 – a + 3) = 7a2 + 13a + 8 – – 5a2 – a – 3
=(7a2 – 5a2) +(13a + a)+ (8 – 3)
= 2a2 + 14a + 5
Question 10.
If A = 4x2 + y2 – 6xy;
B = 3y2+ 12x2 + 8xy;
C = 6x2 + 8y2 + 6xy
Find (i) A + B + C (ii) (A – B) – C
Solution:
(i) im 7
(ii) (A – B) – C
(A – B) = (4x2 + y2 – 6xy) – (3y2 + 12x2 + 8xy)
= (4x2 – 12x2) + (y2 – 3y2) + ( – 6xy – 8xy)
A – B = – 8x2 – 2y2 – 14xy
∴ (A – B) – C = ( – 8x2 – 2y2 – 14xy) – (6x2 + 8y2 + 6xy)
= ( – 8x2 – 6x2) + -2y2 – 8y2) + ( – 14xy – 6xy)
= – 14x2 – 10y2 – 20xy
∴ (A – B) – C = – (14x2 + 10y2 + 20xy)
![]()
iii) 2A + B
2A = 2(4x2 + y2 – 6xy) = 8x2 + 2y2 – 12xy
∴ 2A + B = (8x2 + 2y2 – 12xy) + (3y2 + 12x2 + 8xy)
= (8x2 + 12x2) + (2y2 + 3y2) + ( – 12xy + 8xy)
∴ 2A + B = 20x2 + 5y2 – 4xy
iv) A – 3B
38 = 3(3y2 + 12x2 + 8xy) = 9y2 + 36x2 + 24xy
∴ A – 3B = (4x2 + y2 – 6xy) – (9y2 + 36x2 + 24xy)
= (4x2 – 36x2) (y2 – 9y2) ( 6xy – 24 xy)
= 32x2 – 8y2 – 30xy
∴ A – 3B = – 32x2 – 8y2 – 30xy (or)
= – [32x2 + 8y + 30xy]