AP SCERT 8th Class Maths Textbook Solutions Chapter 10 అనులోమ మరియు విలోమ అనుపాతములు Ex 10.3 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 10th Lesson అనులోమ మరియు విలోమ అనుపాతములు Exercise 10.3
ప్రశ్న 1.
సిరి వద్ద, కిలో 8 రూపాయల చొప్పున 5 కిలోల బంగాళ దుంపలు కొనుటకు సరిపడ డబ్బులు కలవు. బంగాళదుంపల వెల కిలో 10 రూపాయలకు పెరిగిన ఆమె వద్ద వున్న సొమ్ముతో ఎన్నికిలోలు కొనగలదు?
సాధన.
బంగాళదుంపల ధర పెరిగిన వాటిని కొను డబ్బు విలువ తగ్గును.
∴ అవి విలోమానుపాతంలో ఉంటాయి.
∴ x1y1 = x2y2
⇒ 8 × 5 = 10 × x
⇒ x = \(\frac{8 \times 5}{10}\) = 4 కిలోలు.
∴ ఆమె కిలో బంగాళదుంపలు ₹ 10 చొప్పున 4 కిలోలు కొనగలదు.
![]()
ప్రశ్న 2.
ఒక శిబిరంలో 500 మంది వ్యక్తులకు 70 రోజులకు సరిపడు ఆహార ధాన్యాల నిల్వ కలదు. ఆ శిబిరంలో అదనంగా 200 మంది చేరిన ఆ ఆహారధాన్యాల నిల్వ ఎన్ని రోజుల వరకు సరిపోతుంది?
సాధన.
వ్యక్తుల సంఖ్య, వారికి కావలసిన ఆహార పరిమాణం విలోమానుపాతంలో ఉంటాయి.
∴ x1y1 = x2y2
⇒ 500 × 70 = (500 + 200) × x
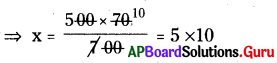
∴ x = 50 రోజులు
ప్రశ్న 3.
36గురు కూలీలు ఒక పనిని 12 రోజులలో చేయగలరు. అయిన అదే పనిని 9గురు కూలీలు ఎన్ని రోజులలో చేయగలరు?
సాధన.
కూలీల సంఖ్య, వారు పనిచేయు రోజుల సంఖ్య విలోమానుపాతంలో కలవు.
∴ x1y1 = x2y2
⇒ 36 × 12 = 9 × x
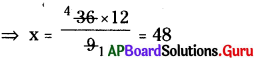
∴ x = 48 రోజులు
![]()
ప్రశ్న 4.
ఒక వ్యక్తి సైకిల్ పై 28 కి.మీ. దూరమును 2 గంటలలో చేరును. అతను అదే వేగముతో ప్రయాణించిన 56 కి.మీ. దూరమును ఎంతకాలములో చేరగలడు?
సాధన.
దూరము – కాలము అనులోమానుపాతంలో ఉంటాయి.

∴ x = 4 గం ||లు
ప్రశ్న 5.
ఒక ఓద గంటకు 16 నాటికల్ మైళ్ళ వేగముతో కొంత దూరమును 10 గంటలలో చేరగలదు. అదే దూరము 8 గంటలలో చేరవలెనన్న ఆ ఓడ ఎంత అధిక వేగముతో ప్రయాణము చేయాలి? సముద్రములపై దూరమునకు ప్రమాణము నాటికల్మై ల్ (1 నాటికల్ మైల్ = 1852 మీటర్లు)
సాధన.
వేగము – దూరం విలోమానుపాతంలో ఉంటాయి.
⇒ x1y1 = x2y2
⇒ 16 × 10 = x × 8
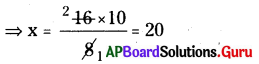
∴ ఆదనంగా పెంచాల్సిన ఓడ వేగం
= 20 – 16 = 4
= 4నాటికల్ మైళ్ళు
![]()
ప్రశ్న 6.
ఒక ట్యాంకును 5 కుళాయిలు 1\(\frac {1}{2}\) గంటల కాలములో సింపును. అదే ట్యాంకును అర్ధగంటలో నింపవలెనన్న అటువంటి కుళాయిలు ఎన్ని కావలెను?
సాధన.
కుళాయిల సంఖ్య, వాటిని నింపే కాలం విలోమాను పాతంలో ఉంటాయి.

∴ కావలసిన కుళాయిల సంఖ్య = 15
ప్రశ్న 7.
15 మంది కూలీలు ఒక గోడను 48 గంటలలో కట్టగలరు. అదే గోడను 30 గంటలలోనే కట్టవలెనన్న ఎంతమంది కూలీలు కావలెను?
సాధన.
కూలీల సంఖ్య, కాలానికి విలోమానుపాతంలో ఉంటుంది.
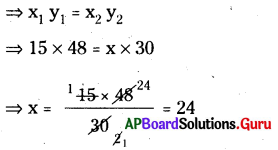
∴ కావలసిన కూలీల సంఖ్య = 24
![]()
ప్రశ్న 8.
ఒక పాఠశాలలో 45 నిమిషముల కాలవ్యవధితో 8 పీరియడ్లు కలవు. ఒక రోజులో 6 పీరియడ్లు మాత్రమే వుండవలెనన్న ఒక పీరియడు కాలవ్యవధి ఎంత వుండవలెను? (పాఠశాల పనివేళలలో మార్పులేదని భావించుము)
సాధన.
కాలానికి, పీరియడ్ల సంఖ్య విలోమానుపాతంలో ఉంటుంది.
⇒ x1y1 = x2y2
⇒ 45 × 8 = x × 6
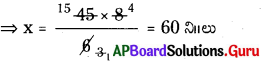
ప్రశ్న 9.
z అనే రాశి x అనే రాశితో అనులోమానుపాతంలోను, y అనే రాశితో విలోమానుపాతంలోను వుంటుంది. x రాశిలో 12% పెరుగుదల, y రాశిలో 20% తరుగుదల వున్న z రాశిలో వచ్చే పెరుగుదల శాతమును కనుగొనుము.
సాధన.
z ∝ x —————– (1)
z ∝ \(\frac {1}{y}\) ————- (2)
(1), (2) ల నుండి z ∝ \(\frac {x}{y}\)
z = k(\(\frac {x}{y}\))
⇒ k = \(\frac {yz}{x}\)
∴ \(\frac{y_{1} z_{1}}{x_{1}}=\frac{y_{2} z_{2}}{x_{2}}\) —————- (3)
∴ x1 = 100x
x2 = 112x (∵ x లో 12% పెరుగుదల)
y1 = 100y
y2 = 80y (∵ y లో 20% పెరుగుదల)
z1 = 100z z2 = ?
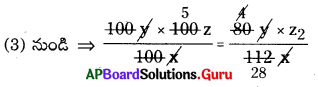
⇒ 5z = \(\frac{\mathrm{z}_{2}}{28}\)
⇒ z2 = 140z
∴ z లో పెరుగుదల శాతం = 40%
![]()
ప్రశ్న 10.
(x + 1) మంది పనివారు ఒక పనిని (x + 1) రోజులలో చేయగలరు. అయిన అదే పనిని (x + 2) మంది పనివారు ఎన్ని రోజులలో చేయగలరు?
సాధన.
పనివారి సంఖ్య, రోజుల సంఖ్యకు విలోమానుపాతంలో ఉంటుంది.
⇒ x1y1 = x2y2
⇒ (x + 1) (x + 1) = (x + 2) × k
⇒ k = \(\frac{(x+1)(x+1)}{(x+2)}\)
∴ k = \(\frac{(x+1)^{2}}{(x+2)}\) రోజులు
ప్రశ్న 11.
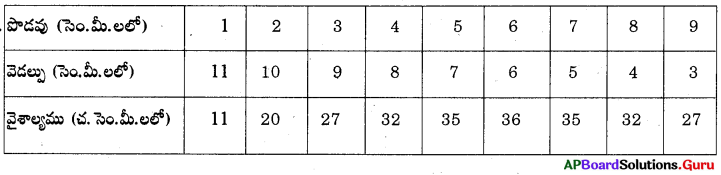
ఒక దీర్ఘచతురస్రము చుట్టుకొలత 24 మీ. దాని చుట్టుకొలతను మార్పుచేయకుండా పొడవును 1 మీ. పెంచినపుడు, దాని వెడల్పు మరియు వైశాల్యములలో మార్పు వచ్చును. క్రింది పట్టికను నింపి ఆ విలువల ఆధారంగా వెడల్పు, వైశాల్యముల విలువలు పొడవు విలువ మార్పు మీద ఏవిధంగా ఆధారపడతాయో గమనించుము. మీరు ఏమి గమనించారు? మీ పరిశీలనను నోట్ పుస్తకములో వ్రాయండి.

సాధన.