AP Board 8th Class Maths Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం InText Questions

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం InText Questions

ఇవి చేయండి

1. ఈ కింది సంఖ్యలలో దిగువ గీత గీయబడిన అంకెల యొక్క స్థాన విలువలు రాయండి. (పేజీ నెం. 312)
(i) 29879
(ii) 10344
(iii) 98725
సాధన.
(i) 29879
8 యొక్క స్థాన విలువ = 8 × 100 – 800
2 యొక్క స్థాన విలువ – 2 × 10,000 = 20,000
(ii) 10344
4 యొక్క స్థాన విలువ = 4 × 1 = 4
3 యొక్క స్థాన విలువ = 3 × 100 = 300
(iii) 98725
5 యొక్క స్థాన విలువ = 5 × 1 = 5
8 యొక్క స్థాన విలువ = 8 × 1000 = 8,000

2. కింది సంఖ్యలను విస్తరణ రూపంలో వ్రాయండి. (పేజీ నెం. 313)
(i) 65
(ii) 74
(iii) 153
(iv) 612
సాధన.
సంఖ్య – విస్తరణ రూపం
(i) 65 = 60 + 5 = (6 × 10¹) + (5 × 10⁰)
(ii) 74 = 70 + 4 = (7 × 10¹) + (4 × 10⁰)
(iii) 153 = 100 + 500 + 3 = (1 × 10²) + (5 × 10¹) + (3 × 10⁰)
(iv) 612 = 600 + 10 + 2 = (6 × 10²) + (1 × 10¹) + (2 × 10⁰)

3. కింది సంఖ్యల విస్తరణ రూపాల్ని, సాధారణ రూపంలోకి మార్చండి. (పేజీ నెం. 313)
(i) 10 × 9 + 4
(ii) 100 × 7 + 10 × 4 + 3
సాధన.
విస్తరణ రూపం – సాధారణ రూపం
(i) 10 × 9 + 4 = 90 + 4 = 94
(ii) 100 × 7 + 10 × 4 + 3 = 700 + 400 + 3 = 743

4. కింది ఖాళీలు పూరించండి. (పేజీ నెం. 313)
సాధన.
(i) 100 × 3 + 10 × _______ + 7 = 357 (5)
(ii) 100 × 4 + 10 × 5 + 1 = _______ (451)
(iii) 100 × _______ + 10 × 3 + 7 = 737 (7)
(iv) 100 × _______ + 10 × q + r = \(\overline{\mathrm{pqr}}\) (p)
(v) 100 × x + 10 × y + z = _________ (\(\overline{\mathrm{xyz}}\))

5. దిగువ 82తో ప్రారంభించి సహజసంఖ్యలను వెనుకకు 1 వరకు వ్రాయగా వచ్చు సంఖ్య ఇవ్వబడినది. మీకు ఇది తెలుసా? (పేజీ నెం. 313)
82818079787776757473727170696867666564636261605958575655545352515049484746454443424140393837363534333231302928272625242322212019181716151413
ఇందులో ఎన్ని అంకెలున్నాయి ? ఇంత పెద్దదయిన ఇది ప్రధాన సంఖ్యయో !
సాధన.
ఇందు అంకెల సంఖ్య 155

6. కింది సంఖ్యల యొక్క కారణాంకాలన్నింటిని వ్రాయండి. (పేజీ నెం. 314)
సాధన.
(a) 24 = 1, 2, 3, 4, 6, 8, 12,24
(b) 15 = 1, 3, 5, 15
(c) 21= 1, 3, 7, 21
(d) 27 = 1, 3, 9, 27
(e) 12= 1, 2, 3, 4, 6, 12
(f) 20 = 1, 2, 4, 5, 10, 20
(g) 18 = 1, 2, 3, 6, 9, 18
(h) 23 = 1, 23
(i) 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36

7. కింది సంఖ్యల యొక్క మొదటి 5 గుణిజాలు వ్రాయండి. (పేజీ నెం. 314)
(a) 5
(b) 8
(c) 9
సాధన.
(a) 5 = 5, 10, 15, 20, 25
(b) 8 = 8, 16, 24, 32, 40
(c) 9 = 9, 18, 27, 36, 45

8. కింది సంఖ్యలను ప్రధాన కారణాంకాల లబ్ధంగా వ్రాయండి. (పేజీ నెం. 314)
(a) 72
(b) 158
(c) 243
సాధన.
(a) 72 = 2 × 2 × 2 × 3 × 3
(b) 158 = 2 × 79
(c) 243 = 7 × 7 × 7

9. కింది సంఖ్యలు 10 తో నిశ్శేషముగా భాగింపబడునో, లేదో తెలపండి. (పేజీ నెం. 315)
(a) 3860
(b) 234
(c) 1200
(d) 10³
(e) 10 + 280 + 20
సాధన.
(a) 3860, (c) 1200, (d) 10³ = 1000, (e) 10 + 280 + 20 = 310ల నుండి (a), (c), (d), (e)లు 10చే నిశ్శేషంగా భాగింపబడును.
[∵ పై సంఖ్యలలో ఒకట్ల స్థానంలోని అంకె సున్న]
(b) 234, 10 చే భాగింపబడదు.
[∵ 234లో ఒకట్ల స్థానంలోని అంకె ‘0’ కాదు. కావున ఇది 10చే భాగింపబడదు. ]

10. కింది సంఖ్యలు 10 తో నిశ్శేషముగా భాగింపబడునో లేదో తెలపంది. (పేజీ నెం. 315)
(a) 10¹⁰
(b) 2¹⁰
(c) 10³ + 10¹
సాధన.
a) 10¹⁰ = 10000000000
b) 2¹⁰ = 1024
c) 10³ + 10¹ = 1000 + 10 = 1010
పై సంఖ్యలలో a, c లు 10 చే నిశ్శేషంగా భాగింపబడును.
b 10చే నిశ్శేషంగా భాగింపబడదు.
ఎందుకనగా 1024లో ఒకట్ల స్థానంలోని అంకె “సున్న” కాదు.

11. కింది సంఖ్యలు 5 చే నిశ్శేషముగా భాగింపబడునో లేదో తెలపండి. (పేజీ నెం. 315)
(a) 205
(b) 4560
(c) 402
(d) 105
(e) 235785
సాధన.
ఒక సంఖ్య ‘5’చే నిశ్శేషంగా భాగింపబడవలెనన్న ఆ సంఖ్యలోని ఒకట్ల స్థానంలోని అంకె ‘0’ లేక ‘5’ అయి ఉండవలెను.
(a) 205 (d) 105 (e) 235785 సంఖ్యలలోని ఒకట్ల స్థానంలోని అంకె ‘5’ కావునా ఇవి ‘5’చే నిశ్శేషంగా భాగింపబడును.
(b) 4560 లో ఒకట్ల స్థానంలోని అంకె ‘O’ కావున ఇది (5’చే నిశ్శేషంగా భాగింపబడుతుంది.
(c) 402 యొక్క ఒకట్ల స్థానంలోని అంకె ‘2’ కావున ఇది ‘5’చే భాగింపబడదు.

12. కింది సంఖ్యలు 3 లేక 9 లేక రెండింటితోను నిశ్శేషముగా భాగింపబడునో, లేదో భాజనీయతా నియమముల ఆధారంగా తెలపండి. (పేజీ నెం. 318)
(a) 3663
(b) 186
(c) 342
(d) 18871
(e) 120
(f) 3789
(g) 4542
(h) 5779782
సాధన.

13. కింది సంఖ్యలు ‘6’ తో నిశ్శేషముగా భాగింపబడునో లేదో తెలపండి.
(a) 1632
(b) 456
(c) 1008
(d) 789
(e) 369
(f) 258
సాధన.

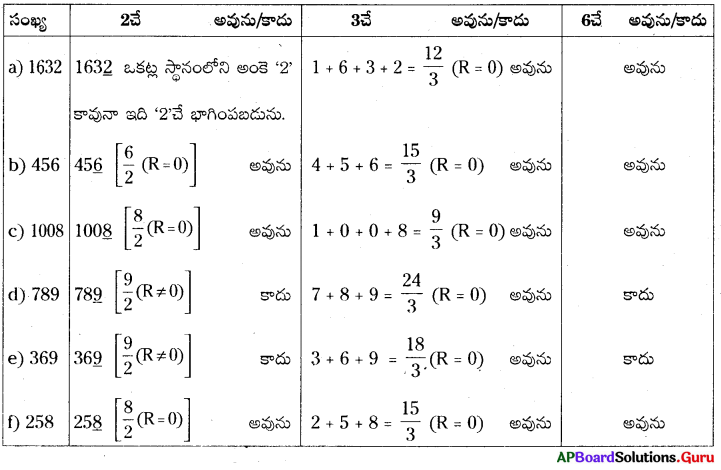
14. కింది సంఖ్యలు ‘6’చే నిశ్శేషముగా భాగింపబడునో, లేదో తెలపండి.
(a) 458 + 676
(b) 6³
(c) 6² + 6³
(d) 2² × 3²
సాధన.

15. 1, 2, 3, 4, 5, 6, 7, 8, 9 అంకెలతో, మొదటి రెండంకెలతో ఏర్పడు సంఖ్య 2చే భాగించబడునట్లు, మొదటి మూడంకెలచే ఏర్పడు సంఖ్య 3చే భాగించబడునట్లు, మొదటి నాలుగంకెలచే ఏర్పడు సంఖ్య 4చే భాగించబడునట్లు మరియు ఇదే క్రమము 9 అంకెల వరకు కొనసాగించగలుగు సంఖ్యను తయారుచేయగలదా? సాధన. 123654987 క్రమపు సంఖ్య సమస్యకు సాధనగా కనిపిస్తుంది. పరీక్షించి సరిచూడండి.
సాధన.

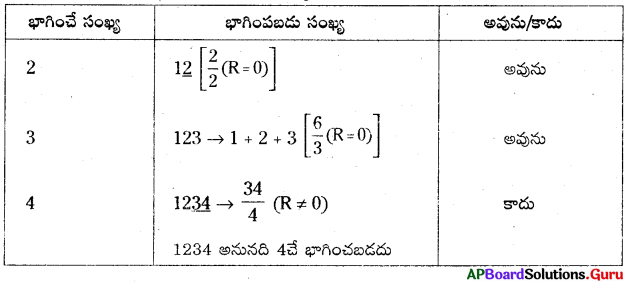
కావున ఈ సంఖ్యను 9 వరకు కొనసాగించలేము.
→ 123654987
2 : 12 → \(\frac {2}{2}\)(R = 0) 2 చే భాగింపబడును.
3 : 123 → 1 + 2 + 3 → \(\frac {6}{3}\)(R = 0) అవును
4 : 1236 → \(\frac {36}{4}\)(R = 0) అవును
5 : 12365 → \(\frac {5}{5}\)(R = 0) అవును

9 123654987 → 1 + 2 + 3 + 6 + 5 + 4 + 9 + 8 + 7 → \(\frac {45}{9}\)(R = 0) అవును
∴ 123654987 క్రమపు సంఖ్యలోని మొదటి రెండంకెలు 2తోను, మొదటి మూడంకెలు 3తోను. ఈ విధంగా చివరి
వరకు అన్ని సందర్భాలలో భాగింపబడుట లేదు.

16. కింది సంఖ్యలు 4 లేక 8 లేక రెండింటితోను భాగింపబడునో, లేదో భాజనీయతా నియమం ప్రకారం తెలపండి.
(a) 464 (b) 782 (c) 3688 (d) 100 (e) 1000 (f) 387856 (g) 4⁴ (h) 8³ (పేజీ నెం. 321)
సాధన.
ఒక సంఖ్య 4చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని చివరి రెండంకెలు ‘4’చే నిశ్శేషంగా భాగింపబడవలెను.
ఒక సంఖ్య ‘8’చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని చివరి మూడంకెలు ‘8’చే నిశ్శేషంగా భాగింపబడవలెను.

17. కింది సంఖ్యలు, 11చే భాగింపబడునో లేదో భాజనీయతా నియమము ద్వారా కనుక్కోండి. (పేజీ నెం. 323)
(i) 4867216 (ii) 12221 (iii) 100001
సాధన.
ఒక సంఖ్య ’11’చే భాగింపబడవలెనన్న “ఆ సంఖ్య యొక్క సరి స్థానాలలోని అంకెల మొత్తం మరియు బేసి స్థానాలలోని అంకెల మొత్తాల భేదం 11 యొక్క గుణిజం లేదా ‘0’ అయి ఉండవలెను.

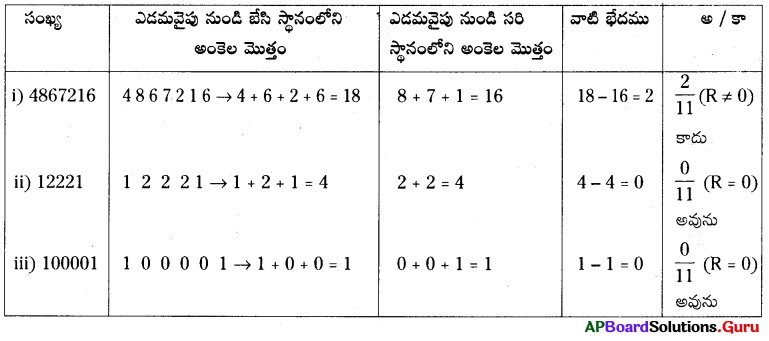
18. వివిధ సంఖ్యల జతలు తీసుకుని వాటికి పై నాలుగు నియమములు సరి చూడండి. (పేజీ నెం. 325)
సాధన.
(a) ‘a’ అను సంఖ్య ‘b’ చే భాగింపబడిన అది ‘b’ యొక్క అన్ని కారణాంకములచే భాగింపబడును.
ఉదా : 36 యొక్క కారణాంకం 18
18 యొక్క కారణాంకాలు = 1, 2, 3, 6, 9, 18
కావున 36, 18 యొక్క అన్ని కారణాంకాలచే భాగింపబడును.
(b) ‘a’, ‘b’ లు పరస్పర ప్రధానసంఖ్యలైనపుడు a మరియు b చే భాగించబడు సంఖ్య a × b తో కూడా భాగింపబడును.
ఉదా : 60 ఒక సంఖ్య. ఇది 3, 4 లచే భాగింపబడును. మరియు 3 × 4 = 12 చే కూడా 60 భాగింపబడును.
(c) “రెండు సంఖ్యలు, వేరువేరుగా మూడవ సంఖ్యతో భాగింపబడుచున్నచో, వాటి మొత్తం కూడా మూడవ సంఖ్యతో భాగింపబడును. ఉదా : ఏవైనా రెండు సంఖ్యలు 18, 9లు తీసుకొందాం. 18, 9 లు 3చే భాగింపబడును. నాటి మొత్తము 18 + 9 = 27 కూడా ‘3’ చే భాగింపబడును.
(d) “రెండు సంఖ్యలు, వేరువేరుగా మూడవ సంఖ్యతో భాగింపబడినట్లయితే, వాటి భేదం కూడా మూడవ సంఖ్యచే భాగింపబడును”.
ఉదా : 25, 30 లు ఏవేని రెండు సంఖ్యలు అనుకొనుము. ఇవి ‘5’ చే భాగింపబడును. వాటి భేదం 30 – 25 = 5 కూడా ‘5’ చే భాగింపబడును.

19. 144, 12 చే భాగించబడును. 144, 12 యొక్క అన్ని కారణాంకములచే భాగింపబడునో, లేదో పరిశీలించండి. (పేజీ నెం. 325)
సాధన.
12 యొక్క కారణాంకాలు = 1, 2, 3, 4, 6, 12
∴ 144, 12 యొక్క అన్ని కారణాంకాలచే భాగింపబడును.

20. 2³ + 2⁴ + 2⁵, 2తో భాగింపబడునో లేదో తెలపండి. వివరించండి. (పేజీ నెం. 325)
సాధన.
2³ + 2⁴ + 2⁵ = 8 + 16 + 32 = 56. ఒక సరి సంఖ్య కావునా ఇది ‘2 చే భాగింపబడును.

21. 3³ – 3², 3 తో భాగింపబడునో లేదో తెలపండి. వివరించండి. (పేజీ నెం. 325)
సాధన.
3³ – 3² = 27 – 9 = 18 → 1 + 8 = → \(\frac {9}{3}\) (R = 0) కావున ఇది ‘3’చే భాగింపబడును.

22. రాజు తలచుకున్న సంఖ్యకు బదులుగా కింది సంఖ్యలు తీసుకుని ఫలితమును సరి చూడండి.. (పేజీ నెం. 328)
(i) 37 (ii) 60 (iii) 18 (iv) 89
సాధన.
(i) 37 సంఖ్యలోని అంకెలను తారుమారు చేయగా వచ్చు సంఖ్య = 73
∴ 37 + 73 → \(\frac {110}{11}\) (R = 0) కావున ఇది ’11’చే భాగింపబడుతుంది.

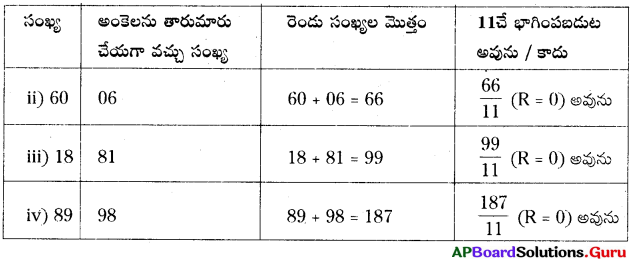
23. ఒక క్రికెట్ టీమ్ నందు 11 మంది ఆటగాళ్ళు కలరు. క్రికెట్ బోర్డు వారికి 10x + y టీ షర్ట్స్ కొనుగోలు చేసింది. తిరిగి బోర్డ్ 10y + x టీ షర్ట్స్ కొనుగోలు చేసింది. మొత్తం టీ షర్ట్స్ అందరికీ సమంగా పంచితే, ఎన్ని టీ షర్ట్స్ మిగులుతాయి? ఒక్కొక్కరికి ఎన్ని టీ షర్ట్స్ వస్తాయి? (పేజీ నెం. 328)
సాధన.
టీమ్ నందు గల ఆటగాళ్ళ సంఖ్య = 11
మొదట కొనుగోలు చేసిన టీ షర్ట్స్ సంఖ్య = 10x + y
రెండవసారి కొనుగోలు చేసిన టీ షర్ట్స్ సంఖ్య = 10y + x
∴ మొత్తం టీ షర్ట్స్ సంఖ్య = (10x + y) + (10y + x)
= 11x + 11y
∴ 11x + 11y = 11(x + y) టీ షర్టులను 11 మందికి సమంగా పంచగా ఒక్కొక్కరికి లభించు టీషర్ట్స్
= \(\frac{11(x+y)}{11}\) = (x + y)
∴ మిగిలిన టీ షర్టుల సంఖ్య = కొనుగోలు చేసిన టీషర్ట్స్ సంఖ్య – 11 × (ఒక్కొక్కరికి లభించు టీషర్ట్స్ సంఖ్య)
= 11 (x + y) – 11 (x + y) = 0

24. ఒక బుట్టలో 10a + b (a ≠ 0 మరియు a > b) పండ్లు కలవు. అందు 10b + a పండ్లు కుళ్ళినవి. మిగిలిన పండ్లను 9మందికి సమానంగా పంచగలమా ? ఒక్కొక్కరికి ఎన్ని పండ్లు వస్తాయి? (పేజీ నెం. 328)
సాధన.
ఒక బుట్టలో గల పండ్ల సంఖ్య = 10a + b
ఆ బుట్టలో కుళ్ళిన పండ్ల సంఖ్య = 10b + a
ఆ బుట్టలో మిగిలిన మంచి పండ్ల సంఖ్య = (10a + b) – (10b + a)
= 10a + b – 10b – a
= 9a – 9b = 9(a – b)
∴ 9(a – b) పండ్లను 9 మందికి సమానంగా పంచగలము.
∴ 9(a – b) పండ్లను 9 మందికి సమానంగా పంచగా ఒక్కొక్కరికి వచ్చు పండ్ల సంఖ్య = 9(a – b) + 9 = (a – b)

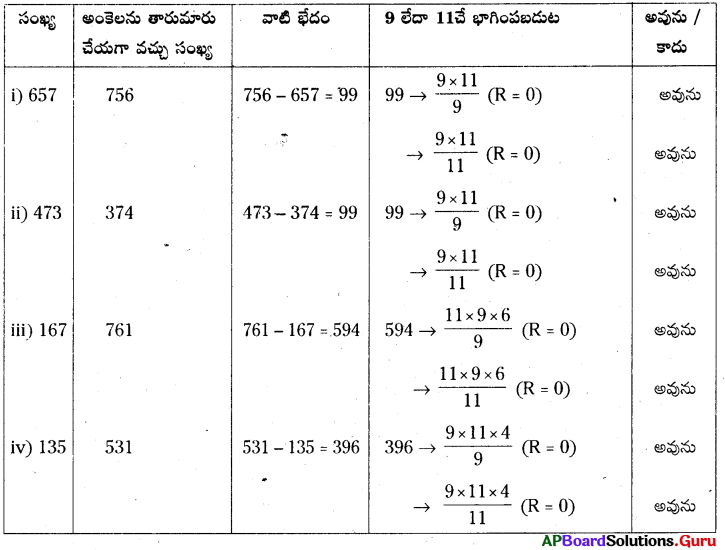
25. పై పజిల్ నందు కింది అంకెలు తీసుకుని పరిశీలించండి. (పేజీ నెం. 329)
(i) 657 (ii) 473 (iii) 167 (iv) 135
సాధన.

26. 21358AB, 99 తో భాగింపబడిన A, B విలువలు కనుక్కోండి. (పేజీ నెం. 331)
సాధన.
21358AB, 99 చే భాగింపబడవలెనన్న అది ‘9’చే మరియు ’11’చే భాగింపబడవలెను.
21358AB, 9చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం 9చే భాగింపబడవలెను.
∴ 2 + 1 + 3 + 5 + 8 + A + B = (9 × 3) = 27 అనుకొనుము.
A + B = 27 – 19 = 8 ⇒ A + B = 8 ………………. (1)
21358AB, ’11’ చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని బేసి స్థానాలలోని అంకెల మొత్తం నుండి సరి స్థానాలలోని అంకెల మొత్తాన్ని తీసివేయగా వచ్చిన దానిని ’11’ నిశ్శేషంగా భాగించవలెను.
2 1 3 5 8 A B
⇒ (2 + 3 + 8 + B) – (1 + 5 + A) = 11 × 1 అనుకొనుము.
⇒ 13 + B – 6 – A = 11
⇒ B – A = 11 – 7 = 4 ………………. (2)
(1), (2) ల నుండి A = 2, B = 6
∴ 21358AB = 2135826, 99 చే నిశ్శేషంగా భాగింపబడును.

27. 4AB8, వరుసగా 2, 3, 4, 6, 8, 9 లచే భాగింపబడిన A, B విలువలు కనుగొనుము. (పేజీ నెం. 331)
సాధన.
ఇచ్చిన సంఖ్య 4AE → \(\frac {8}{2}\) (R = 0) కావున ఇది ‘2’ చే భాగింపబడుతుంది.
4AB8 → ‘3’చే భాగింపబడవలెనన్న సంఖ్యలోని అంకెల మొత్తం 3 యొక్క గుణిజం కావలెను.
∴ 4 + A + B + 8 = 3 లేదా 6 లేదా 9/12/15/18
∴ A + B + 12 = 3/6/9/12/15/18 ………………. (1)
4AB8 → \(\frac {B8}{4}\) ⇒ B = 2, 4, 6, 8 కావలెను …………………………. (2)
4AB8 → \(\frac {AB8}{8}\) ⇒ AB = 12, 16, 24, 28, 32, 36, …….
4ABB8 → ‘9’చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం 9 యొక్క గుణిజం కావలెను.
∴ 4 + A + B + 8 = 9, 18, 27 ……
A + B + 12 = 9, 18, 27, ……. ………………….(3)
(1), (3) ల నుండి A + B + 12 = 9 లేదా 18 తీసుకోనగా
A + B + 12 = 9 అయిన A + B = – 3
∴ ఇది సరైనది కాదు
A + B + 12 = 18 అయిన
⇒ A + B = 18 – 12 = 6
∴ A + B = 6
A = 4, B = 2 అయిన
4AB8 = 4428
→ \(\frac {428}{8}\)(R ≠ 0)
∴ A = 2, B = 4
(లేదా)
A = 2, B = 4 అయిన
4AB8 = 4248
→ \(\frac {248}{8}\) (R = 0)

28. పై పద్ధతి ఉపయోగించి, 7810364 సంఖ్య, 4చే భాగింపబడుతుందో, లేదో పరిశీలించండి. (పేజీ నెం. 333)
సాధన.
ఇచ్చిన సంఖ్య = 7810364

స్థానవిలువల శేషములను, ఆ సంఖ్య అంకెలతో గుణించగా వచ్చు లబ్దాల మొత్తం = 0 + 0 + 0 + 0 + () + 12 + 4
→ \(\frac {16}{4}\)(R = 0)
∴ 7810364, 4 చే భాగింపబడును.

29. పై పద్ధతి ఉపయోగించి 963451, 6తో భాగింపబడుతుందో, లేదో పరిశీలించండి. (పేజీ నెం. 333)
సాధన.
ఇచ్చిన సంఖ్య = 963451

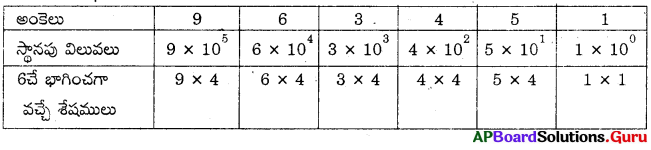
స్థాన విలువల శేషములను, ఆ సంఖ్య అంకెలతో గుణించగా వచ్చు లబ్దాల మొత్తం
= 36 + 24 + 12 + 16 + 20 + 1 → \(\frac {109}{6}\) (R ≠ 0)
∴ 963451. 6 చే భాగింపబడదు.

ప్రయత్నించండి

ప్రశ్న 1.
56Z అను సంఖ్య 10 తో భాగించిన వచ్చు శేషము 6. అయితే Z యొక్క విలువ కనుక్కోండి. (పేజీ నెం. 315)
సాధన.
56Z అను సంఖ్యలో Z = 0, 1, 2, 3, 4, …….. 9 గా తీసుకొనవలెను.
10చే భాగించగా శేషం ‘6’ రావలెనన్న Z = 6 ను తీసుకొనగా

ప్రశ్న 2.
4B ను 5 తో భాగించిన ‘1’ శేషము వచ్చును. అయిన Bకు ఏయే విలువలు ఉండవచ్చును ? (పేజీ నెం. 316)
సాధన.
4B ను 5చే భాగించగా శేషం ‘1’ రావలెనన్న B = {0, 1, 2, 3, …….. 9} నుండి అనగా 40, 41, 42, 43, 44, 45, 46, ……, 49ల నుండి 41, 46 ను తీసుకొనిన ఇవి ‘5’చే భాగించగా శేషం ‘1’ని ఇస్తాయి. ∴ B = {1, 6}

ప్రశ్న 3.
76C ను 5 తో భాగించిన ‘2’ శేషము వచ్చును. అయిన Cకు ఏయే విలువలు ఉండవచ్చును ? (పేజీ నెం. 316)
సాధన.
76C ను 5 చే భాగించగా శేషం ‘2’ వచ్చుటకు C = {0, 1, ……. 9} నుండి C = 2, 7 గా తీసుకొనిన 762, 767 లు 5చే భాగించిన శేషం ‘2’ను ఇస్తాయి. ∴ C = {2,7}

ప్రశ్న 4.
“ఒక సంఖ్య 10 తో నిశ్శేషముగా భాగింపబడిన, 5తో కూడా నిశ్శేషముగా భాగింపబడుతుంది” ఈ వాక్యము సత్యమో/ అసత్యమో తెలపండి.
దానికి తగు కారణము తెలపండి. (పేజీ నెం. 316)
సాధన.
ఇచ్చిన వాక్యం సత్యం. ఎందుకంటే ఒక సంఖ్య ’10’చే నిశ్శేషంగా భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె ‘0’ (సున్న) అయి ఉండవలెను.

అదేవిధంగా ఒక సంఖ్య ‘5’చే భాగింపబడవలెనన్న ఆ సంఖ్య యొక్క ఒకట్ల స్థానంలో 0 లేదా 5 ఉండాలి.
∴ 10చే భాగింపబడే ప్రతి సంఖ్య, 5చే కూడా భాగింపబడుతుంది.

ప్రశ్న 5.
“ఒక సంఖ్య 5తో నిశ్శేషముగా భాగింపబడిన, 10తో కూడా నిశ్శేషముగా భాగింపబడుతుంది” ఈ వాక్యము సత్యమో/ – అసత్యమో తెలపండి. దానికి తగు కారణము తెలపండి. (పేజీ నెం. 316)
సాధన.
ఇచ్చిన వాక్యం అసత్యం. ఎందుకంటే ఒక సంఖ్య 5 చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె ‘0’ (సున్న) గాని, 5 గాని ఉండవలెను. కాని 10చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకే ‘0’ (సున్న) మాత్రమే అయి ఉండవలెను.
∴ 5 చే భాగింపబడే ప్రతి సంఖ్య 10 చే భాగింపబడదు.

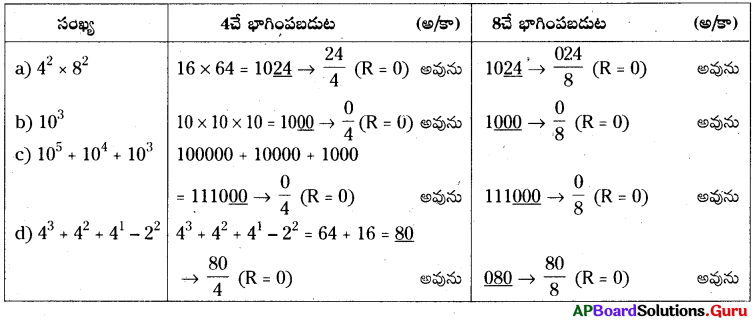
6. కింది సంఖ్యలు 4 లేక 8 లేక రెండింటితోను భాగింపబడునో లేదో తెలపండి. (పేజీ నెం. 321)
(a) 4² × 8²
(b) 10³
(c) 10⁵ + 10⁴ + 10³
(d) 4³ + 4² + 4¹ – 2²
సాధన.

7. కింది సంఖ్యలు 7చే భాగించబడుతాయా ? పరీక్షించండి. (పేజీ నెం. 322)
(a) 322 (b) 588 (c) 952 (d) 553 (e) 448
సూచన : ఒక మూడంకెల సంఖ్య ‘7’ చే భాగింపబడవలెనన్న (2a + 3b + C) ‘7’ చే భాగింపబడవలెను.
సాధన.

∴ పై సంఖ్యలన్నియూ ‘7’చే నిశ్శేషంగా భాగింపబడును.

8. నాలుగంకెల సంఖ్యను సాధారణ రూపంలో తీసుకొని ‘7తో భాజనీయతా నియమాన్ని తయారుచేయండి. (పేజీ నెం. 322)
సాధన.
నాలుగంకెల సంఖ్య abcd అనుకొనుము.

∴ ఒక నాలుగు అంకెల సంఖ్య ‘7’చే భాగింపబడవలెనన్న, (6a + 2b + 3c + d) అనేది ‘7’ చే భాగింపబడవలెను.

9. 3192, 7 యొక్క గుణకము “నీ నియమముతో” సరిచూడండి. (పేజీ నెం. 322)
సాధన.
ఇచ్చిన సంఖ్య → 3192 ⇒ a = 3, b = 1, c = 9, d = 2
6a + 2b + 3c + d = 6 × 3 + 2 × 1 + 3 × 9 + 2
= 18 + 2 + 27 + 2 = 49 → \(\frac {49}{7}\) (R= 0)
∴ 3192 నా నియమం ప్రకారం ‘7’చే భాగింపబడును.

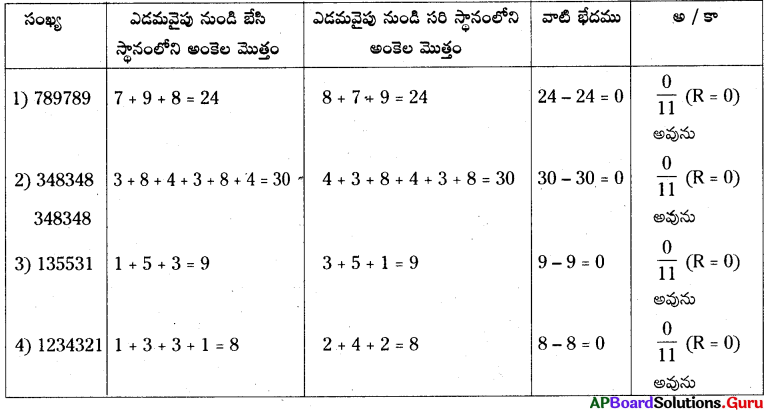
10. (1) 789789, 11చే భాగింపబడునో, లేదో పరిశీలించండి. (పేజీ నెం. 323)
(2) 348348348348, 11చే భాగింపబడునో, లేదో పరిశీలించండి.
(3) 135531 ఒక సరి పాలిండ్రోమ్ సంఖ్య. ఈ సంఖ్య 11చే భాగింపబడునో, లేదో తెలపండి.
(4) 1234321, 11చే భాగింపబడుతుందో, లేదో తెలపండి.
సాధన.

11. 1576 × 1577 × 1578 తో ఏర్పడు సంఖ్య 3తో భాగింపబడునో, లేదో కారణముతో తెలపండి. (పేజీ నెం. 325)
సాధన.
ఇచ్చిన సంఖ్య = 1576 × 1577 × 1578
ఏ మూడు వరుస సంఖ్యల లబ్దమైనా ‘3’చే భాగింపబడుతుంది.
ఉదా : 4 × 5 × 6 = 120 → \(\frac {120}{3}\) (R = 0)
∴ 1576 × 1577 × 1578 లు మూడు వరుస సంఖ్యలు కావున వాని లబ్ధం ‘3’చే భాగింపబడుతుంది.

12. పై పద్ధతి ద్వారా, 10 అంకెలు కల పెద్ద సంఖ్యను వ్రాసి 11 యొక్క భాజనీయతా సూత్రము సరిచూడండి. (పేజీ నెం. 326)
సాధన.
10 అంకెల పెద్ద సంఖ్య = 9,99,99,99,999
D C B A
∴ 9 / 999 / 999 / 999
⇒ B + D = 9 + 999 = 1008
A + C = 999 + 999 = 1998
∴ (A + C) – (B + D) = 990 → \(\frac {990}{11}\) (R = 0)
∴ ఈ భాజనీయతా సూత్రము ద్వారా “10 అంకెల పెద్ద సంఖ్య ’11’చే నిశ్శేషంగా భాగింపబడుతుంది” అని నిరూపించగలం.

13. ఒక మూడు అంకెల సంఖ్యను తీసుకుని, దాని యొక్క అంకెల అమరిక మార్చుతూ (ABC, BCA, CAB అగునట్లు) మూడు సంఖ్యలను తయారుచేయండి. ఆ మూడు సంఖ్యలను కలిపి, వచ్చు ఫలితము ఏయే సంఖ్యలతో భాగింపబడునో పరిశీలించండి. (పేజీ నెం. 329)
సాధన.

14. YE × ME = TTT అయిన Y + E + M + T ల మొత్తం కనుగొనుము. (పేజీ నెం. 332)
(సూచన : TTT = 100T + 10T + T = T(111) = T(37 × 3))
సాధన.
TTT = 100T + 10 T + T
= T(111) = T(37 × 3)
∴ YE × ME = T(37 × 3)
∴ T = {1, 2, 3, ….. 9}
కాని T = {3, 6, 9} అనునవి 3 యొక్క గుణిజాలు

∴ T(37 × 3) = 3(111), 6(111), 9(111) 3 భాగించబడును.
∴ YE × ME = 333 / 666 / 999
∴ YE × ME = 999 = 27 × 37
∴ Y = 2, M = 3, E = 7, T = 3
∴ Y + E + M + T = 2 + 7 + 3 + 3 = 15

15. 88 వస్తువుల ఖరీదు A733B అయిన A, B విలువలు కనుక్కోండి. (పేజీ నెం. 332)
సాధన.
A733B, 88 చే భాగింపబడవలెనన్న ఆ సంఖ్య 8 × 11 చే భాగింపబడవలెను.
ఒక సంఖ్య ’11’ చే భాగింపబడవలేనన్న బేసి స్థానాలలోని అంకెల మొత్తం, సరి స్థానాలలోని అంకెల మొత్తాల మధ్య గల భేదం ‘0’ లేదా 11చే భాగింపబడవలెను.
A 7 3 3 B ⇒ (A + 3 + B) – (7 + 3) = 0
⇒ A + B = 7
A733B, 8 చే భాగింపబడవలెనన్న చివరి మూడంకెలు 8చే భాగింపబడవలెను.
A733B ⇒ \(\frac {33B}{8}\)
∴ B = 6 [∵ \(\frac {336}{8}\) (R = 0)]
∴ A + B = 7 నుండి B = 6 అయిన
A + 6 = 7 ⇒ A = 7 – 6 = 1
∴ A = 1, B = 6

16. 456456456456 అను సంఖ్య 7, 11 మరియు 13తో కూడా భాగింపబడునో లేదో ప్రయత్నించి చూడండి. (పేజీ నెం. 334)
సాధన.
ఇచ్చిన సంఖ్య = 456456456456
456456456456 = 456 (1001001001) = 456 × (7 × 11 × 13) × (1000001)
∴ 456456456456 అను సంఖ్య 7, 11 మరియు 13 చే భాగింపబడుతుంది.

ఆలోచించి, చర్చించి వ్రాయండి

1. ఒక సంఖ్య 5 మరియు 2 చే భాగింపబడునపుడు వచ్చు శేషములు వరుసగా 3 మరియు 1 అయిన ఆ సంఖ్య యొక్క ఒకట్ల స్థానములోని అంకెను కనుగొనుము. (పేజీ నెం. 316)
సాధన.
ఒక సంఖ్య 5 మరియు 2 చే భాగింపబడునపుడు శేషములు 3 మరియు 1 అయిన అందలి ఒకట్ల స్థానంలోని అంకె 3. ఉదా : \(\frac {13}{5}\) ⇒ 3 శేషం \(\frac {13}{2}\) ⇒ 1 శేషం
\(\frac {23}{5}\) ⇒ 3 శేషం \(\frac {23}{2}\) ⇒ 1 శేషం

2. ఒక రెండంకెల సంఖ్యను తీసుకుని వాటి అంకెలను తారుమారు చేసి వ్రాయండి. వచ్చిన సంఖ్యలలో పెద్ద సంఖ్య నుండి చిన్న సంఖ్యను తీసివేయండి. వచ్చిన ఫలితము ఎల్లప్పుడూ 9తో భాగింపబడునా? (పేజీ నెం. 328)
సాధన.

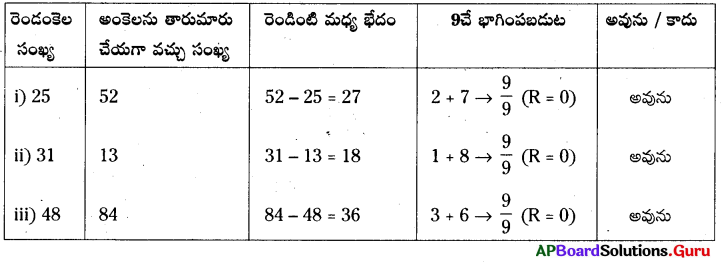
∴ ఫలితము ఎల్లప్పుడూ 9తో భాగింపబడుతుంది.

3. (1) 10²ⁿ – 1, 9 మరియు 11 చే భాగింపబడునని చెప్పగలమా ? వివరించండి.
(2) 10^{2n + 1} – 1, 11 చే భాగింపబడునో, లేదో పరిశీలించండి. (పేజీ నెం. 333)
సాధన.

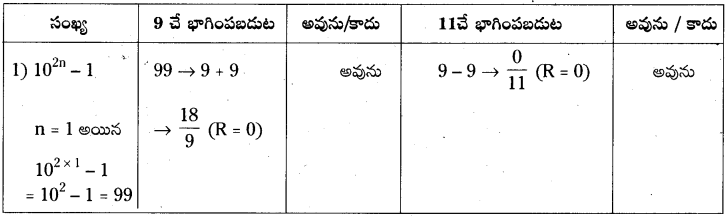
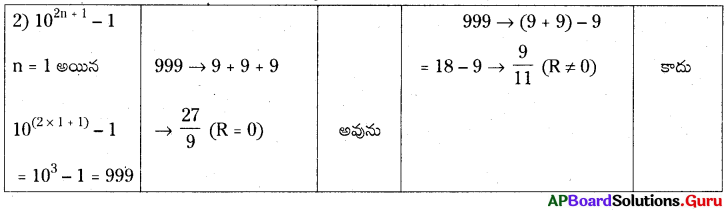
4. a⁵ + b⁵, (a + b) తో భాగింపబడుతుందో లేదో a, b విలువలు ఏవైనా సహజ సంఖ్యలుగా తీసుకుని ప్రయత్నించండి. (పేజీ. నెం. 334)
సాధన.

5. (a^{2n + 1} + b^{2n + 1}), (a + b) తో భాగింపబడునని చెప్పగలమా? (పేజీ నెం. 334)
సాధన.

∴ a^{2n + 1} + b^{2n + 1} అనునది n యొక్క అన్ని విలువలకు (a + b) చే భాగింపబడుతుంది.