SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు InText Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు InText Questions
ఇవి చేయండి
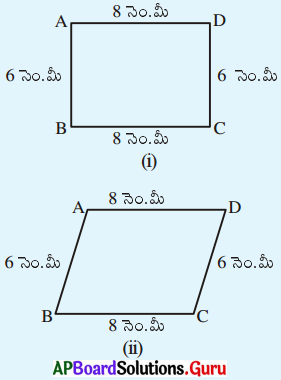
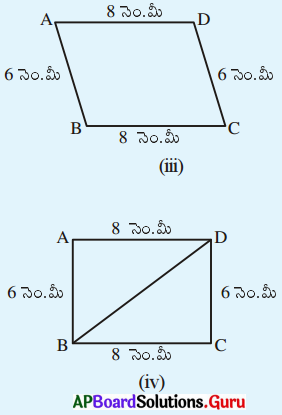
1. 8 సెం.మీ. పొడవు గల ఒక జత కర్రపుల్లలు తీసుకోండి. అదేవిధంగా 6 సెం.మీ. పొడవు గల మరొక జత కర్రపుల్లలు తీసుకోండి. వీటితో ఒక దీర్ఘచతురస్రాకారాన్ని 6 సెమీ) ఏర్పరచండి. ఈ దీర్ఘ చతురస్రం ఇవ్వబడిన 4 కొలతలతో (పుల్లలు) ఏర్పడింది. దీనిని వెడల్పు పుల్ల వెంబడి నెమ్మదిగా, కదిలించండి. ఏర్పడిన ఈ కొత్త రకం ఆకారం పూర్వపు ఆకారమేనా ? పటం (ii) లో ఏర్పడిన చతుర్భుజానికి కొత్త రూపం వచ్చింది కదా ! ముందు దీర్ఘచతురస్రం ఇప్పుడు సమాంతర చతుర్భుజం అయింది. నీవు ఏమైన కర్రపుల్లల కొలతలు మార్చావా ? లేదు కదా ! భుజాల పొడవులు అదేవిధంగా ఉన్నాయి. కొత్తగా ఏర్పడిన చతుర్భుజ రూపాన్ని మరొకసారి వ్యతిరేక దిశలో కదిలించండి. చతుర్భుజా ఏ రూపం వచ్చింది ? తిరిగి మరలా సమాంతర చతుర్భుజం వచ్చింది. కాని ఇది పూర్తిగా వొక రూపం అని పటం (iii) చూసి గమనించవచ్చు. ఈ సందర్భంలోనూ నాలుగు కొలతలు ఒకే విధంగా ఉన్నాయి. దీనిని బట్టి నాలుగు కొలతలతో ఏకైక చతుర్భుజం ఏర్పడదని తెలుసుకోవచ్చు. మరి అయిదు కొలతలు ఒక ఏకైక చతుర్భుజాన్ని ఏర్పరుస్తాయా? తిరిగి మనం కృత్యాన్ని కొనసాగిద్దాం . 8 సెం.మీ., 6 సెం.మీ. పొడవులు గల రెండు జతల పుల్లలతో దీర్ఘచతురస్రాన్ని ఏర్పరిచారు కదా ! పటం (iv) లో చూపిన విధంగా BD పొడవుకు సమానమయ్యే మరొక కర్రపుల్లను చేరుద్దాం. ఇప్పుడు ముందుగా చేసినట్లుగా వెడల్పు వెంబడి కదిపి చూడండి. ఆకారంలో మార్పు వచ్చిందా ? లేదు కదా! మార్పు చెందలేదని గమనిస్తారు. అందుచే ఐదవ కొలత (పుల్ల) దీర్ఘ చతురస్రాకారాన్ని మార్చడానికి వీలు లేకుండా చేయగలిగింది. మరొక రకమైన చతుర్భుజం ఏర్పడే అవకాశం లేకుండా ‘ (కొలతలు మార్చనంత వరకు) జరిగింది. దీనిని బట్టి ఒక చతుర్భుజం ఏకైకంగా ఏర్పడాలంటే ఐదు కొలతలు అవసరమని తెలుస్తున్నది. మరి. ఏ ఐదు కొలతలైనా ఏకైక చతుర్భుజాన్ని ఏర్పరచడానికి సరిపోతాయా ? (పేజీ నెం. 60)
సాధన.
అవును, సరిపోతాయి.
![]()
2. కావల్సిన సామగ్రి : కొలబద్ద, మూలమట్టాలు మరియు కోణమానిని. (పేజీ నెం. 61)
గుర్తుంచుకోవల్సినవి : రేఖలు సమాంతరాలో కాదో తెలుసుకొనుటకు మూలమట్టాలను మొదటి రేఖ నుండి రెండవ రేఖ వైపు జరపాలి.
కింది పటాలలో ధర్మాలను పరిశీలించడానికి తగు పరికరాలు ఎంచుకొని పరిశోధించి రాయండి.
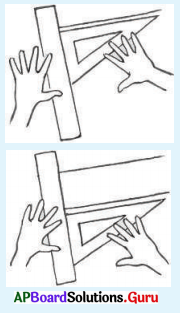
ప్రతి చతుర్భుజానికి
a) ఎదుటి భుజాలు సమాంతరమో, కాదో చూడాలి.
b) ప్రతి కోణం కొలత కనుగొనాలి.
c) ప్రతి భుజం పొడవు కనుగొనాలి.
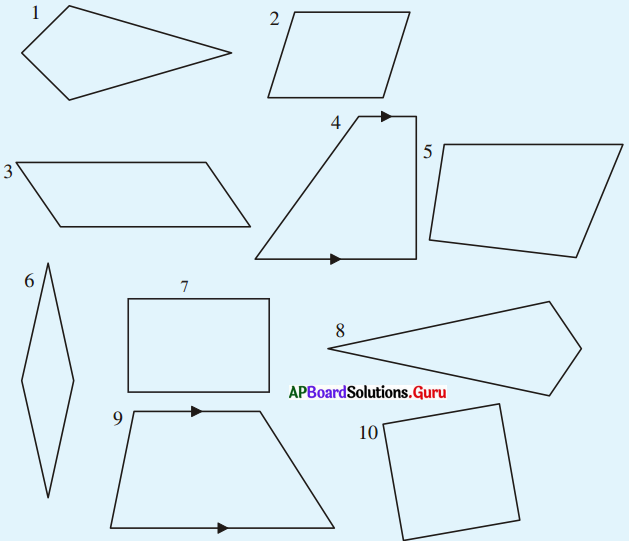
మీరు పరిశోధించి కనుగొన్న ఫలితాలను పట్టికలో నమోదు చేయండి.
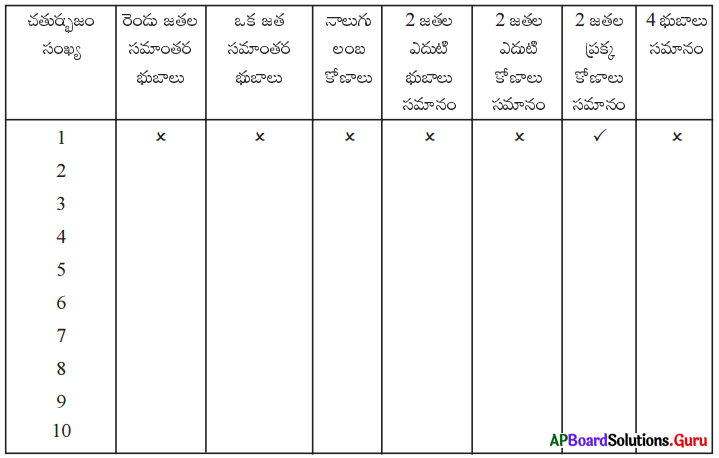
సాధన.
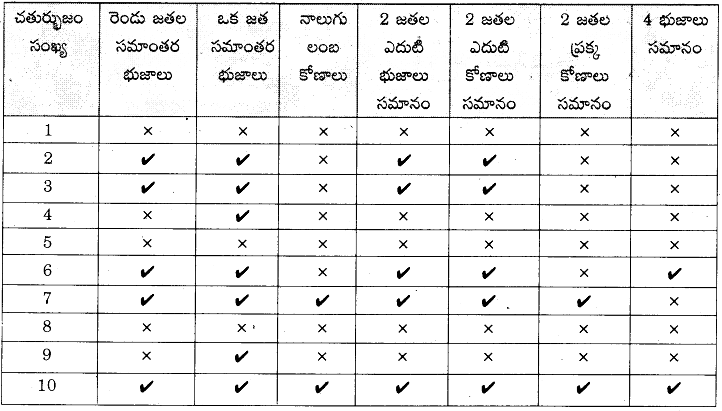
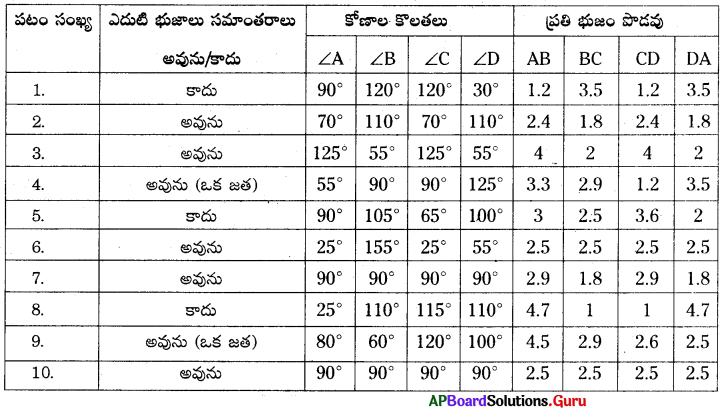
![]()
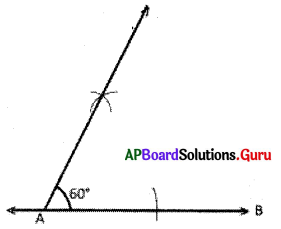
3. 60° కోణాన్ని గీయగలరా ? (పేజీ నెం. 63)
సాధన.
వృత్తలేఖిని, స్కేలును ఉపయోగించి 60° కోణాన్ని నిర్మించవచ్చు.
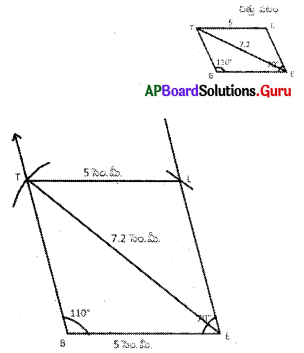
4. BELT సమాంతర చతుర్భుజాన్ని, మరి ఏ ఇతర సమాంతర చతుర్భుజ ధర్మాల ఆధారంగా నిర్మించవచ్చో తెలిపి, నిర్మించి చూడండి. (పేజీ నెం. 75)
సాధన.
ఒక భుజం, ఒక కర్ణము, ఒక కోణం ఆధారంగా సమాంతర చతుర్భుజాన్ని నిర్మించవచ్చు.
BE = 5 సెం.మీ. ⇒ LT = 5 సెం.మీ.
∠B = 110° ⇒ ∠E = 180° – 110° = 70°
TE = 7.2 సెం.మీ.
![]()
ప్రయత్నించండి (పేజీ నెం. 70)
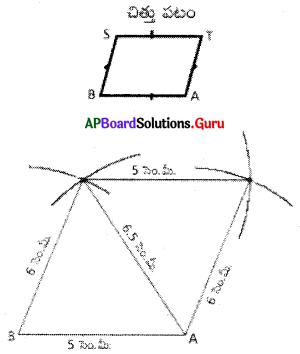
1. BA = 5 సెం.మీ., AT = 6 సెం.మీ. మరియు AS = 6.5 సెం.మీ. కొలతలతో BATS సమాంతర చతుర్భుజం గీయగలమా? వివరించండి.
సాధన.
BATS సమాంతర చతుర్భుజంలో ఎదురెదురు భుజాలు సమానాలు.
∴ BA = ST = 5 సెం.మీ., AT = BS = 6 సెం.మీ., AS = 6.5 సెం.మీ.
∴ BATS సమాంతర చతుర్భుజాన్ని నిర్మించవచ్చు.
ఎందుకనగా దీనికి 3 స్వతంత్ర కొలతలు చాలు.
2. ఒక విద్యా ర్థి PL = 3 సెం.మీ., LA = 4 సెం.మీ., AY = 4.5 సెం.మీ., PY = 2 సెం.మీ. మరియు LY = 6 సెం.మీ. కొలతలతో PLAY అనే చతుర్భుజాన్ని నిర్మించడానికి ప్రయత్నించాడు. కాని సాధ్యం కాలేదు. ఎందుకు ? నీవు కూడా చతుర్భుజాన్ని గీయడానికి ప్రయత్నించి, తగు కారణాలు తెల్పండి.
సాధన.
PLAY అను చతుర్భుజ కొలతలు
PL = 3 సెం.మీ.
LA = 4 సెం.మీ.
AY = 4.5 సెం.మీ.
PY = 2 సెం.మీ.
LY = 6 సెం.మీ.
ఇచ్చట YP + PL < YL
(త్రిభుజం YPL లో రెండు భుజాల మొత్తం 3వ భుజం కంటే ఎక్కువగా ఉండాలి. కానీ ఈ సందర్భంలో అలా సంభవించలేదు. )
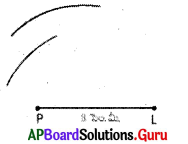
PLAY అనునది ఒక చతుర్భుజం కాదు.
(∵ YL > YP)
∴ ఇచ్చిన కొలతలతో చతుర్భుజం నిర్మించలేము.
(ఎందుకనగా L నుండి గీసిన చాపము P నుండి గీసిన చాపములు ఖండించుకొనుటలేదు. Y, P, L లు ఒకే సరళరేఖపై కలవు. )
![]()
ఆలోచించి, చర్చించి వ్రాయండి (పేజీ నెం. 63)
1. ప్రతి దీర్ఘచతురస్రం ఒక సమాంతర చతుర్భుజమేనా ? ప్రతి సమాంతర చతుర్భుజం ఒక దీర్ఘచతురస్రమేనా ?
సాధన.
అవును. ప్రతి దీర్ఘచతురస్రం ఒక సమాంతర చతుర్భుజం అగును. కాని ప్రతి సమాంతర చతుర్భుజం ఒక దీర్ఘ చతురస్రం కాదు.
2. ఉమ బెల్లం చక్కని దీర్ఘచతురస్రాకారంలో చేయాలనుకున్నది. అది దీర్ఘచతురస్రాకారంలోనే వుండాలంటే ఆమె దానిని ఎన్ని రకాలుగా పరిశీలించి ఆకారం తీసుకురావాలి ?
సాధన.
బెల్లం చక్కీని దీర్ఘచతురస్రాకారంలోనికి మార్చాలంటే దానిని i) చతుర్భుజం ii) సమలంబ చతుర్భుజం iii) సమాంతర చతుర్భుజాకారాలను పరిశీలించాలి.
3. AB = 4.5 సెం.మీ., BC = 5.2 సెం.మీ., CD = 4.8 సెం.మీ., కర్ణాలు AC = 5 సెం.మీ. మరియు BD = 5.4 సెం.మీ. కొలతలు గల ABCD చతుర్భుజాన్ని గీయడానికి ముందుగా ΔABDతో మొదలు పెట్టి నాల్గవ శీర్షం ‘C’ ని గుర్తించగలరా ? కారణాలు తెలపండి. (పేజీ నెం. 72)
సాధన.
ΔABD నిర్మించడం సాధ్యం కాదు కావునా ముందుగా ΔABD తో మొదలు పెట్టి ABCD చతుర్భుజాన్ని నిర్మించడం సాధ్యం కాదు. [∵ AD పొడవు ఇవ్వబడలేదు)
4. PQ = 3 సెం.మీ., RS = 3 సెం.మీ., PS = 7.5 సెం.మీ., PR = 8 సెం.మీ. మరియు SQ = 4 సెం.మీ. కొలతలతో PORS చతుర్భుజం నిర్మించండి. నిర్మాణం ఏవిధంగా చేస్తారో వివరించండి. (పేజీ నెం. 72)
సాధన.
PQ = 3 సెం.మీ. RS = 3 సెం.మీ. PS = 7.5 సెం.మీ. PR = 8 సెం.మీ. SQ = 4 సెం.మీ.
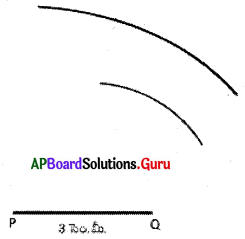
∴ ఇచ్చిన కొలతలతో PQS త్రిభుజం నిర్మించలేము.
PQ+ QS < PS
∴ S శీర్షం నిర్మించవలెనన్న P నుండి గీసిన చాపం మరియు Q నుండి గీసిన చాపాలు ఖండించుకొనుట లేదు.
∴ S శీర్షం లేకుండా PQRS చతుర్భుజ నిర్మాణం సాధ్యం కాదు.
![]()
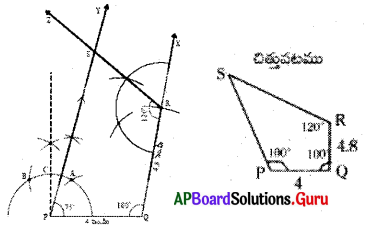
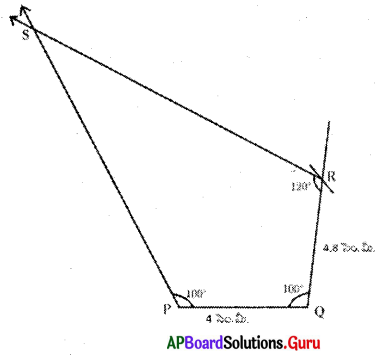
5. ప్రక్క పటంలో ఇచ్చిన కొలతలలో ∠P = 75°కు బదులు ∠P= 100° తీసుకుంటే PQRS చతుర్భుజం నిర్మించగలరా ? కారణాలు తెలపండి. (పేజీ నెం. 74)
సాధన.
PQ = 4 సెం.మీ., QR = 4.8 సెం.మీ.,
∠P = 100°, ∠Q = 100°, ∠R = 120°
∴ ఇచ్చిన కొలతలతో PQRS చతుర్భుజం నిర్మించ గలం. ఎందుకనగా 4 కోణాల మొత్తం = 360°
6. PL = 6 సెం.మీ., LA = 9.5 సెం.మీ., ∠P = 75°, L = 15° మరియు ∠A = 140° కొలతలతో PLAN చతుర్భుజం గీయగలరా ? (పేజీ నెం. 74)
(ప్రతి సందర్భంలోనూ చిత్తు పటాలను గీచి, కొలతలను విశ్లేషించండి.) మీ యొక్క సమాధానాలకు తగిన కారణాలు తెలపండి.
సాధన.
PL = 6 సెం.మీ., LA = 9.5 సెం.మీ., ∠P = 75°, ∠L = 15°, ∠A = 140°
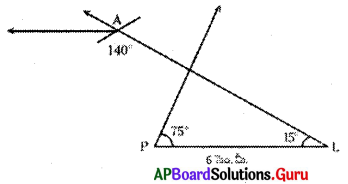
∴ ఇచ్చిన కొలతలతో PLAN చతుర్భుజం నిర్మించలేము.
7. AB = 5 సెం.మీ., BC = 4.5 సెం.మీ., CD = 6 సెం.మీ., ∠B = 100°, ∠C = 75° కొలతలు గల ABCD చతుర్భుజాన్ని BC భూమిగా తీసుకొని (AB భూమిగా కాకుండా) నిర్మించగలరా ? చిత్తుపటం గీచి నిర్మాణ సోపానాలను వివరించుము. (పేజీ నెం. 77)
సాధన.
AB = 5 సెం.మీ., BC = 4.5 సెం.మీ., CD = 6 సెం.మీ., ∠B = 100°, ∠C = 75°
నిర్మాణ క్రమం :
1. 4.5 సెం.మీ.ల వ్యాసార్ధంతో BC రేఖాఖండాన్ని నిర్మించితిని.
2. B, C లు కేంద్రాలుగా 100°; 75° వరుస కిరణాలు గీచితిని.
3. B, C లు కేంద్రాలుగా 5 సెం.మీ., 6 సెం.మీ., వ్యాసార్ధాలతో రెండు చాపాలను గీయగా అవి కిరణాలను ఖండించిన బిందువులను A, D లుగా గుర్తించితిని.
4. A, D లను కలిపితిని.
5. ∴ ABCD చతుర్భుజం ఏర్పడినది.
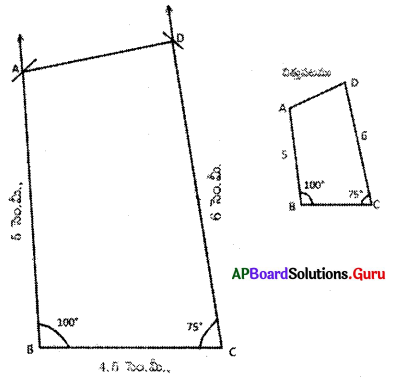
![]()
8. ప్రక్క పటంలో ABCD రాంబస్ ను AC భూమిగా తీసుకొని నిర్మించగలరా ? లేదంటే కారణాలు తెలపండి. (పేజీ నెం. 79)
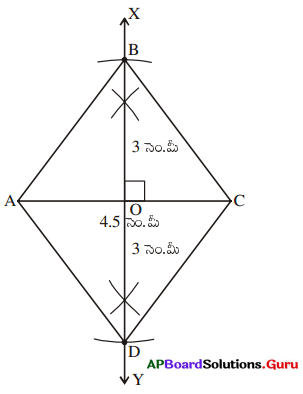
సాధన.
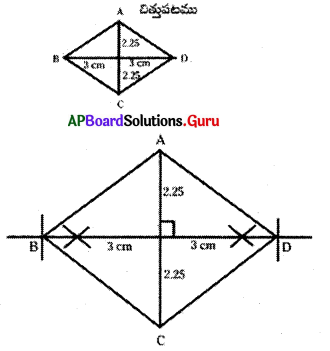
ABCD రాంబస్ లో AC భూమి కాకుండా BD ను భూమిగా తీసుకొని రాంబసను నిర్మించవచ్చు.
9. రాంబస్ లో రెండు కర్ణాల పొడవులు సమానం అయితే ఏ పటం ఏర్పడుతుంది ? చిత్తుపటం గీచి, తగు కారణాలను తెలపండి. (పేజీ నెం. 79)
(లేదా )
ఒక సమాంతర చతుర్భుజంలోని కర్ణాల పొడవులు సమానం అయిన సందర్భంలో ఏయే పటాలు ఏర్పడునో చిత్తు పటాలు గీచి, తగు కారణాలతో తెల్పండి.
సాధన.
ఒక రాంబ లోని రెండు కర్ణాల పొడవులు సమానం అయిన రాంబస్లో అన్ని భుజాలు సమానంగా ఉంటాయి కావునా అది ఒక చతురస్రం అవుతుంది. ∴ ABCD ఒక చతురస్రం.
[∵ AB = BC = CD = DA & AC = BD]