AP Board 8th Class Maths Solutions Chapter 5 అనుపాతముతో రాశులను పోల్చుట Ex 5.3

SCERT AP 8th Class Maths Solutions Chapter 5 అనుపాతముతో రాశులను పోల్చుట Ex 5.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson అనుపాతముతో రాశులను పోల్చుట Exercise 5.3

ప్రశ్న1.
సుధాకర్ తన ఇంటి మరమ్మత్తుల కొరకు బ్యాంకు నుండి ₹ 15,000 అప్పు తీసుకున్నాడు. అతడు సంవత్సరము నకు 9% వడ్డీరేటు చొప్పున 8 సంవత్సరముల కాలానికి అప్పుతీసుకొనిన, అతడు ప్రతీనెల ఎంత మొత్తము చెల్లించాలి ?
సాధన.
P = 15,000
R = 9%
T = 8 సం॥ = \(\frac {8}{12}\) నెలలు

అతడు నెలనెలా చెల్లించాల్సిన వడ్డీ = ₹ 900

ప్రశ్న2.
ఒక టెలివిజన్ ని ₹ 21,000 లకు కొన్నారు. ఒక సంవత్సరము తరువాత దాని విలువ 5% తగ్గినది (వస్తువుల వాడకము, కాలమును బట్టి వాటి విలువ తగ్గును). ఒక సంవత్సరము తరువాత ఆ టెలివిజన్ విలువ ఎంత?
సాధన.
టెలివిజన్ కొన్న విలువ = ₹ 21,000
ఒక సం॥ తరువాత దాని విలువ = 21000 – 21000 లో 5%

= 21000 – 1050
= ₹ 19,950

ప్రశ్న3.
₹ 8000 లపై 5% వడ్డీ రేటు చొప్పున ప్రతీ సంవత్సరమున కొకసారి వడ్డీ తిరగ కట్టబడిన రెండు సంవత్సరములకు అయ్యే చక్రవడ్డీని, మొత్తమును కనుగొనుము.
సాధన.
P = ₹ 8000; R = 5%
ప్రతి సం॥నకు ఒకసారి చొప్పున వడ్డీ తిరగకట్టిన రెండు సంవత్సరాలకు 2 కాల వ్యవధులు వస్తాయి.
∴ n = 2

∴ మొత్తం (A) = ₹ 8820
చక్రవడ్డీ (C.I.) = మొత్తం – అసలు
= 8820 – 8000 = ₹820

ప్రశ్న4.
₹ 6500 లపై మొదటి సంవత్సరము 5% చొప్పున రెండవ సంవత్సరము 6% వడ్డీ రేటు చొప్పున ప్రతీ సంవత్సరము వడ్డీ తిరిగకట్టబడిన 2 సంవత్సరములకు అయ్యే చక్రవడ్డీని, మొత్తమును కనుగొనుము.
సాధన.
P = ₹ 6500, R = 5%, T = 1 సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{6500 \times 5 \times 1}{100}\)
= 325
∴ A = P + I = 6500 + 325 = 6825
∴ P = 6825 (రెండవ సంవత్సరం మొదట్లో మొత్తం అసలు అగును)
R = 6%, T = 1 సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{6825 \times 6 \times 1}{100}\)
∴ A = P + I = 6825 + 409.5
∴ మొత్తము = ₹ 7234.50
చక్రవడ్డీ = ₹ 409.5

ప్రశ్న5.
ప్రతిభ ఒక ఋణ సంస్థ (ఫైనాన్స్ కంపెనీ) నుండి మొదటి కారును కొనడానికి ₹ 47000 లను 17% వడ్డీ రేటుతో 5 సంవత్సరములకు సాధారణ వడ్డీకి అప్పు తీసుకున్నది. అయిన (a) ఆమె ఋణ సంస్థకు ఎంత మొత్తము చెల్లించాలి. (b) ఆ మొత్తాన్ని సమాన వాయిదాలలో చెల్లించాలంటే ఆమె ప్రతీ నెల ఎంత మొత్తము చెల్లించాలి.
సాధన.
P = ₹47000, R = 17%, T = 5 సం॥

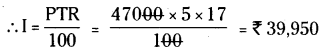
∴ చెల్లించాల్సిన మొత్తం (A) = P + I
= 47000 + 39,950 = 86950
a) ఋణసంస్థకు ఆమె చెల్లించాల్సిన మొత్తం = ₹ 86950
b) ఆ మొత్తాన్ని సమాన వాయిదాల్లో చెల్లించాలంటే ఆమె ప్రతినెల చెల్లించాల్సిన మొత్తం

ప్రశ్న6.
2011వ సంవత్సరములో హైదరాబాదు జనాభా 68,09,000 అది ప్రతీ సంవత్సరము 4.7% చొప్పున పెరుగుచున్న 2015వ సంవత్సరము. చివరి నాటికి హైదరాబాదు జనాభా ఎంత అవుతుంది ?
సాధన.
2011 లో హైదరాబాద్ జనాభా = 68,09,000
ప్రతి సం॥ అది 4.7% చొప్పున పెరుగుచున్న 2015 నాటికి హైదరాబాద్ జనాభా
= 6809000 \(\left(1+\frac{4.7}{100}\right)^{4}\)
[∵ P = 6809000, R = 4.7%, n = 4(2015 – 2011)
= 6809000 × \(\frac{104.7}{100} \times \frac{104.7}{100} \times \frac{104.7}{100} \times \frac{104.7}{100}\)
= ₹ 81,82,199

ప్రశ్న7.
₹ 10,000 లను 8\(\frac {1}{2}\)% చొప్పున సంవత్సరమున కొకసారి వడ్డీ తిరిగి లెక్కకట్టు పద్ధతిలో పొదుపుచేసిన 1 సంవత్సరము 3 నెలల కాలంలో వచ్చే చక్రవడ్డీని కనుగొనండి.
సాధన.
P = ₹ 10,000 ; R = 8\(\frac {1}{2}\)% = \(\frac {17}{2}\)%
T = 1 సం॥

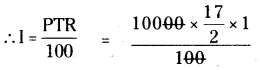
= 50 × 17 = 850
∴ I = ₹ 850
∴ A = P + I = 10,000 + 850
A = 10,850
∴ P = 10,850 ; R = 8\(\frac {1}{2}\)% = \(\frac {17}{2}\)%
T(n) = 3 నెలలు = \(\frac {3}{12}\) సం॥ = \(\frac {1}{4}\) సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{10850 \times \frac{17}{2} \times \frac{1}{4}}{100}\)
= \(\frac{10850 \times 17}{800}\)
I = ₹ 230.5625
∴ అసలు (A) = P + I
= 10850 + 230.5625
= ₹ 11080. 5625

ప్రశ్న8.
ఆరిఫ్ ఒక బ్యాంక్ నుండి ₹ 80,000 లను వడ్డీరేటు 10% చొప్పున అప్పు తీసుకొనెను. (i) సంవత్సరము మరియు (ii) 6 నెలలు తిరిగి వడ్డీ కట్టు కాల వ్యవధులుగా తీసుకొని 1\(\frac {1}{2}\) సంవత్సరములకు వడ్డీ కట్టిన ఆ రెండు మొత్తముల భేదమును కనుగొనుము.
సాధన.
P = ₹ 80,000; R = 10%; T = 1 సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{80000 \times 10 \times 1}{100}\) = 8000
∴ A = P + I = 80000 + 8000 = ₹ 88,000
మరలా 6 నె॥లకు అగు వడ్డీ :
P = 80000
R= 10%
T = 6 నె॥లు
= \(\frac {1}{2}\) సం॥
I = \(\frac{\text { PTR }}{100}\)
= \(\frac{80000 \times \frac{1}{2} \times 10}{100}\)
= 4000

i) ఒక సంవత్సరం 6 నెలల తరువాత కట్టవలసిన మొత్తం = వడ్డీ + అసలు
= 88000 + 4000
A1 = ₹ 92000

ii) 6 నెలలకొకసారి, చక్రవడ్డీ కట్టవలెనన్న 1\(\frac {1}{2}\) సం॥ చొప్పున 3 కాలవ్యవధులు వస్తాయి.
∴ n = 3 అగును.
R = \(\frac {10}{2}\) = 5%
P = ₹ 80,000

∴ రెండు మొత్తాల మధ్య భేదం = A₂ – A₁ = 92610 – 92000
= ₹ 610

ప్రశ్న9.
నేను ప్రసాద్ వద్ద నుండి ₹ 12000 లను 6% వడ్డీ రేటు చొప్పున సాధారణ వడ్డీకి 2 సంవత్సరముల కాలానికి అప్పు తీసుకున్నాను. నేను అదే మొత్తమును 6% వడ్డీ రేటు చొప్పున సంవత్సరమునకొకసారి తిరిగి వడ్డీ కట్టు పద్ధతిన అప్పు తీసుకున్నచో ఎంతసొమ్ము అదనంగా చెల్లించవలసి వస్తుంది ?
సాధన.
ప్రసాదు వద్ద నుండి తీసుకున్న సొమ్ము = (P)
= ₹ 12000
T = 2 సం॥ R = 6%
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{12000 \times 2 \times 6}{100}\)
I = ₹ 1440
మొత్తం = అసలు + వడ్డీ
A₁ = P + I = 12000 + 1440
= ₹ 13440
∴ 2 సం॥ల తరువాత సాధారణ వడ్డీ రేటు 6% చొప్పున చెల్లించాల్సిన మొత్తం = ₹ 13440
చక్రవడ్డీ చొప్పున 2 సం॥ల తరువాత చెల్లించాల్సిన మొత్తం
P = ₹ 12,000, R = 6%, n = 2 సం॥

∴ చక్రవడ్డీ, సాధారణ వడ్డీల ద్వారా వచ్చు మొత్తాలలో భేదం = 13483.2 – 13440
= ₹ 43.20

ప్రశ్న10.
ఒక ప్రయోగశాలలో, ప్రయోగమును నిర్వహించి బాక్టీరియాలో పెరుగుదల రేటు గంటకు 2.5% అని గుర్తించినారు. ప్రారంభంలో బాక్టీరియా సంఖ్య, 5,06,000 లు వున్నచో రెండు గంటల తరువాత ఆ బాక్టీరియా సంఖ్య ఎంత ?
సాధన.
ప్రారంభంలో ప్రయోగశాలలో గల బాక్టీరియాల సంఖ్య = 5,06,060
గంటకు 2.5 % రేటుతో పెరిగిన, 2 గం॥ల తరువాత ఆ బాక్టీరియాల సంఖ్య
∵ n = 2 గం॥లు

ప్రశ్న11.
కమల బ్యాంకు నుండి స్కూటరు కొనే నిమిత్తం ₹26400 లను 15% వడ్డీ రేటు చొప్పున సంవత్సరమున కొకసారి తిరిగి వడ్డీ కట్టు పద్ధతిలో అప్పు తెచ్చుకున్నది. 2 సంవత్సరముల 4 నెలల తరువాత అప్పు మొత్తము తీర్చివేయవలెనన్న ఆమె చెల్లించవలసిన మొత్తమును కనుగొనుము.
సాధన.
కమల బ్యాంకు నుండి తీసుకున్న మొత్తం = ₹ 26400
వడ్డీ రేటు (R) = 15% చొప్పున 2 సం॥లకు అగు మొత్తం

∴ తదుపరి 4 నెలలకు వడ్డీ కట్టుటకు మొత్తం (₹ 34914) అసలు అగును.
∴ P = 34914, R = 15%, T = 4 నెలలు = \(\frac {4}{22}\) సం॥
= \(\frac {1}{3}\) సం॥
I = \(\frac{\mathrm{PTR}}{100}\) = \(\frac{34914 \times 15 \times \frac{1}{3}}{100}\)
= ₹ 1745.7
∴ 2 సం॥ల 4 నెలల కాలానికి కమల బ్యాంక్ వారికి చెల్లించాల్సిన మొత్తం = 34914 + 1745.7
= ₹ 36659.7

ప్రశ్న12.
భారతి ₹ 12500 లను 12% వడ్డీ రేటు చొప్పున 3 సంవత్సరముల కాలానికి సాధారణ వడ్డీకి అప్పు తీసుకున్నది. మాధురి అదే మొత్తాన్ని అదేకాలానికి 10% వడ్డీ రేటుతో సంవత్సరమునకొకసారి తిరిగి వడ్డీ కట్టు పద్ధతిన అప్పుతెచ్చినది. ఆ ఇద్దరిలో ఎవరు ఎక్కువ వడ్డీని చెల్లించెదరు ? ఎంత ఎక్కువ వడ్డీని చెల్లించెదరు?
సాధన.
భారతి తీసుకున్న అసలు సొమ్ము
P = ₹ 12500
R = 12%
T = 3 సం॥లు
సాధారణ వడ్డీ (I) = \(\frac{\mathrm{PTR}}{100}\)
= \(\frac{12500 \times 12 \times 3}{100}\)
= 125 × 36 = 4500
∴ 3 సం॥ల తరువాత చెల్లించాల్సిన మొత్తం
A₁ = P + I = 12500 + 4500
A₁ = ₹ 17,000
మాధురి చక్రవడ్డీ చొప్పున కట్టాల్సిన మొత్తం

∴ A₁ > A₂
A₁ – A₂ = 17000 – 16637.5
= ₹ 362.5
∴ భారతి, మాధురి కంటే ₹ 362.5 ఎక్కువ వడ్డీ చెల్లించాల్సి ఉంటుంది.

ప్రశ్న13.
₹ 10000 ల విలువ గల యంత్ర సామగ్రిలో తరుగుదల రేటు 5%. అయిన 1 సంవత్సరము తరువాత దాని విలువ ఎంత ?
సాధన.
10,000 విలువ గల యంత్రసామాగ్రి 5% తరుగుదల రేటు ప్రకారం 1 సం॥ తరువాత దాని విలువ

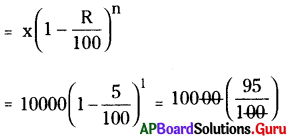
= 95 × 100 = ₹ 9500

ప్రశ్న14.
ఒక పట్టణ ప్రస్తుత జనాభా 12 లక్షలు. సంవత్సరమునకు 4% చొప్పున జనాభా పెరుగుతూ వుంటే 2 సంవత్సరముల తరువాత ఆ పట్టణ జనాభా ఎంత?
సాధన.
పట్టణ ప్రస్తుత జనాభా = 12,00,000
సం॥నకు 4% చొప్పున జనాభా పెరుగుతూ ఉంటే 2 సం॥ల తరువాత ఆ పట్టణ జనాభా

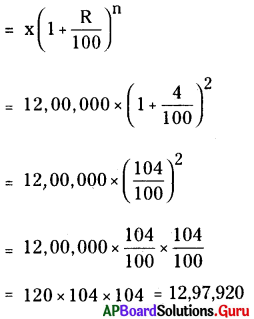
ప్రశ్న15.
₹ 1000 లను 10% వడ్డీరేటు చొప్పున త్రైమాసికంగా తిరిగి వడ్డీ కట్టు పద్ధతిన 1 సంవత్సర కాలానికి అయ్యే చక్రవడ్డీని కనుగొనండి.
సాధన.
₹ 1000 లను 10% వడ్డీ రేటు చొప్పున త్రైమాసికంగా తిరిగి వడ్డీ కట్టిన 1 సం॥కాలానికి అయ్యే మొత్తం
A = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}\)
త్రైమాసికంగా చక్రవడ్డీ కట్టవలెనన్న 1 సం॥నకు 4 కాలవ్యవధులు వస్తాయి.
∴ n = 4, P = 1000, R = \(\frac{10}{4}=\frac{5}{2}\)%
∴ A = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}\)
= \(1000 \times\left(1+\frac{5 / 2}{100}\right)^{4}\)

సం॥ కాలానికి అయ్యే చక్రవడ్డీ = 1103.81 – 1000 = ₹ 103.81