AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1

SCERT AP 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 7th Lesson పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Exercise 7.1

ప్రశ్న1.
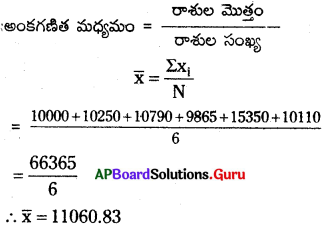
ఒక దుకాణంలో వారంలో జరిగిన అమ్మకాలు రోజు వారీగా ఇవ్వబడ్డాయి. వాటి అంకగణిత మధ్యమము కనుగొనండి.
₹ 10000, ₹ 10250, ₹ 10790, ₹ 9865, ₹ 15350, ₹ 10110
సాధన.
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 1

ప్రశ్న2.
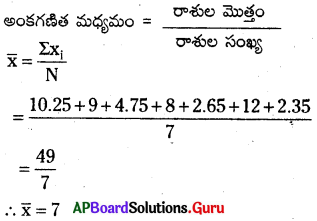
10.25, 9, 4.75, 8, 2.65, 12, 2.35 రాశుల అంకగణిత మధ్యమమెంత ?
సాధన.
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 2

ప్రశ్న3.
8 రాశుల అంకగణిత మధ్యమము 25. వాని నుండి 11 అను రాశిని తొలగించగా మిగిలిన రాశుల అంకగణిత మధ్యమమును కనుగొనండి.
సాధన.
8 రాశుల అంకమధ్యమం = 25
⇒ 8 రాశుల మొత్తం = 25 × 8 = 200
11 అను రాశిని తొలగించగా వచ్చు రాశుల మొత్తం = 200 – 11 = 189
∴ మిగిలిన 7 రాశుల అంకమధ్యమం = \(\frac {189}{7}\) = 27

ప్రశ్న4.
9 రాశుల అంకగణిత మధ్యమము 38 గా లెక్కించబడినది. కానీ అట్లు లెక్కించుటలో 72ను 27గా పొరపాటుగా తీసుకున్నారు. అయిన సరియైన అంక గణిత మధ్యమమును లెక్కించండి.
సాధన.
9 రాశుల అంకమధ్యమం = 38
9 రాశుల మొత్తం = 38 × 9 = 342
72 ను 27 గా తీసుకొనిన సరియైన అంశం 72 – 27 = 45
∴ సరియైన రాశుల మొత్తం = 342 + 45 = 387
∴ సరియైన సగటు = \(\frac {387}{9}\) = 43

ప్రశ్న5.
ఐదు సంవత్సరముల క్రిందట ఒక కుటుంబ సభ్యుల సరాసరి వయస్సు 25 సం॥లు. ప్రస్తుతము ఆ కుటుంబ సభ్యుల సరాసరి వయస్సు ఎంత ? (సభ్యుల సంఖ్యలో మార్పులేదు)
సాధన.
దత్తాంశంలోని అన్ని రాశులకు ఒక సంఖ్యను కూడినా లేక అన్ని రాశుల నుండి ఒక సంఖ్యను తీసివేసినా ఆ దత్తాంశం యొక్క అంకగణిత మధ్యమం కూడా అదే విధంగా మార్పు చెందుతుంది.
5 సం॥ల క్రిందట కుటుంబ సభ్యుల సరాసరి వయస్సు = 25 సం॥లు
ప్రస్తుతం ఆ కుటుంబ సభ్యుల సరాసరి వయస్సు = 25 + 5 = 30 సం॥
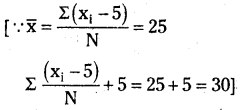
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 3

ప్రశ్న6.
రెండు సం॥ల క్రిందట ఒక సమూహములోని 40 మంది వయస్సుల సగటు వయస్సు 11 సం॥లు. ప్రస్తుతము ఆ సమూహము నుండి ఒక వ్యక్తి బయటకు వెళ్ళిపోగా మిగిలిన సభ్యుల సగటు వయస్సు 12 సం॥లు. అయిన వెళ్ళిపోయిన వ్యక్తి వయస్సు ఎంత ?
సాధన.
ఒక సమూహంలోని 40 మంది వయస్సుల ప్రస్తుత సగటు వయస్సు = (11 + 2) సం॥లు
∴ 40 మంది వయస్సుల మొత్తం = 40 × (11 + 2)
= 40 × 13 = 520 సం॥లు
40 మంది నుండి 1 వ్యక్తి బయటకు వెళ్ళగా మిగిలిన సభ్యుల సంఖ్య = 40 – 1 = 39
39 మంది సగటు వయస్సు = 12 సం॥లు
39 మంది వ్యక్తుల వయస్సుల మొత్తం = 12 × 39 = 468
∴ బయటకు వెళ్ళిన వ్యక్తి వయస్సు = 520 – 468 = 52 సం॥లు

ప్రశ్న7.
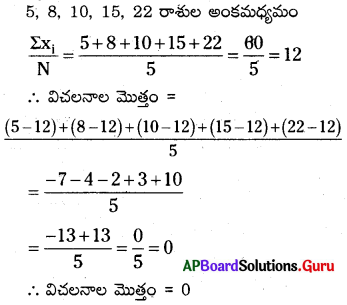
ఒక దత్తాంశములోని 5, 8, 10, 15, 22 అను రాశుల యొక్క అంకగణిత మధ్యమము నుండి వాని విచలనాల మొత్తమును కనుగొనండి.
సాధన.
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 4

ప్రశ్న8.
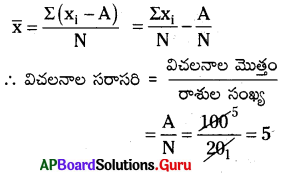
20 రాశుల సరాసరి నుండి వాని విచలనాల మొత్తము 100 అయిన, విచలనముల సరాసరి ఎంత ?
సాధన.
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 5

ప్రశ్న9.
ఒక యూనిట్ పరీక్షలో 12 మంది విద్యార్థులు సాధించిన మార్కులు 4, 21, 13, 17, 5, 9, 10, 20, 19, 12, 20, 14 అయిన ఒక విలువను ఊహించిన అంకగణిత మధ్యమంగా తీసుకొని దత్తాంశమునకు అంకగణిత మధ్యమమును కనుగొనండి. మరియొక సంఖ్యను ఊహించిన అంకగణిత మధ్యమంగా తీసుకొని మరలా సరాసరిని కనుగొనండి. రెండుసార్లు సమాన ఫలితాలు వచ్చినవా ? మీ అభిప్రాయం ఏమిటి ?
సాధన.
ఇచ్చిన రాశులు 4, 21, 13, 17, 5, 9, 10, 20, 19, 12, 20, 14
నేను ఊహించిన అంకమధ్యమం 10 అనుకొనిన,
అంకగణిత మధ్యమం = ఊహించిన అంకగణిత మధ్యమం + విచలనాల సరాసరి
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 6
\(\overline{\mathrm{x}}\) = అంకమధ్యమం = 13.67
మరొక ఊహించిన అంకమధ్యమం 12 అయిన
\(\overline{\mathrm{x}}\) అంకమధ్యమం = ఊహించిన అంకగణిత సగటు + విచలనాల సరాసరి
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 7
\(\overline{\mathrm{x}}\) = 13.67
∴ అన్ని సందర్భాలలో \(\overline{\mathrm{x}}\) = 13.67 అగును.

ప్రశ్న10.
ఒక తరగతిలో 10 మంది విద్యార్థుల మార్కుల సరాసరి 15 (25 మార్కులకు). వారిలో కరిష్మా అనే విద్యార్థి మిగిలిన 9 మంది విద్యార్థులను అడిగి తన కన్నా ఎన్ని మార్కులు ఎక్కువ లేక తక్కువ అనే వివరాలను సేకరించింది. ఆ విచలనాలు – 8, – 6, – 3, – 1, 0, 2, 3, 4, 6. అయిన ఆమెకు వచ్చిన మార్కులెన్ని?
సాధన.
10 మంది విద్యార్థుల సరాసరి = 15 (25 మార్కులకు)
మొత్తం మార్కులు = 10 × 15 = 150,
కరిష్మా మార్కులు = x
9మంది మార్కుల విచలనాలు
= -8, -6, -3, -1, 0, 2, 3, 4, 6
∴ x – 8 + x – 6 + x – 3 + x – 1 + x + 0 + x + 2 + x + 3 + x + 4 + x + 6 + x = 150
10x – 18 + 15 = 150
∴ 10x – 3 = 150
10x = 150 + 3 = 153
x = \(\frac {153}{10}\) = 15.3 మార్కులు
(లేదా)
ఇచ్చిన విచలనాలు = -8, -6, -3, -1, 0, 2, 3, 4, 6
కరిష్మా మార్కులు = x అనుకొనిన
మొత్తం మార్కులు = 10 × 15 = 150
∴ పరిశీలనాంశాలు – -8+ x, – 6 + x, -3 + x, -1 + x, 0 + x, 2 + x, 3 + x, 4 + x, 6 + x అగును.
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 8a
⇒ \(\frac{10 x-18+15}{10}\) = 15 (సగటు = 15 ఇవ్వబడినది)
⇒ 10x – 3 = 150
⇒ 10x = 150 + 3
⇒ 10x = 153
⇒ x = \(\frac {153}{10}\)
x = 15.3 మార్కులు
∴ కరిష్మా పొందిన మార్కులు = 15.3

ప్రశ్న11.
25 అను విలువ నుండి ఒక దత్తాంశములోని n రాశుల విచలనముల మొత్తము 25 మరియు 35 అను విలువ నుండి అవే రాశుల విచలనాల మొత్తం – 25 అయిన ఆ దత్తాంశము యొక్క అంకగణిత సగటు ఎంత ?
సాధన.
25 అను విలువ నుండి ఒక దత్తాంశములోని x రాశుల విచలనముల మొత్తం = Σx₁ = 25
∴ ఈ రాశుల సరాసరి = 25 + \(\frac{\Sigma x_{1}}{n}\) = 25 + \(\frac{25}{n}\)
= \(\frac{25 n+25}{n}\)
35 అను విలువ నుండి అదే రాశుల విచలనాల మొత్తం = Σx₁ = – 25
∴ ఈ రాశుల సరాసరి = 35 + \(\frac{\Sigma x_{1}}{n}\) = 35 + \(\frac{(-25)}{n}\)
= \(\frac{35 n-25}{n}\)
∴ ఆ దత్తాంశము యొక్క సగటు
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 9
(లేదా)
25 నుండి తీసుకొనబడిన విచలనాలు
= x₁, x₂, x₃, …….. x_n అనుకొనుము.
∴ కావలసిన పరిశీలనాంశాలు
= x₁ – 25, x₂ – 25, ……….. + x_n – 25 అగును.
∴ పరిశీలనాంశాల మొత్తం = Σn
⇒ x₁ – 25 + x₂ – 25 + ……….. + x_n – 25 = 25
⇒ (x₁ + x₂ + …… + x_n) – (25n) = 25
⇒ x₁ + x₂ + ……. + x_n = 25 + 25n
= 25 (1 + n) —— (1)
35 నుండి తీసుకొనబడిన విచలనాలు = x₁, x₂, x₃, ……… x_n అనుకొనుము.
∴ కావలసిన పరిశీలనాంశాలు
⇒ x₁ – 35, x₂ – 35, ……… x_n – 35 అగును.
పరిశీలనాంశాల మొత్తం = – 25
∴ (x₁ – 35) + (x₂ – 35) + ……. + (x_n – 35) = – 25
⇒ (x₁ + x₂ + x₃ + …… + x_n) – 35n = – 25
⇒ x₁ + x₂ + x₃ + …… + x_n = – 25 + 35n —— (2)
(1), (2) ల నుండి
25 + 25n = – 25 + 35n
⇒ 10n = 50 ⇒ n = 5
∴ మొత్తం పరిశీలనాంశాల సగటు
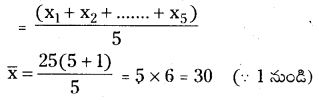
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 10

ప్రశ్న12.
3.3, 3.5, 3.1, 3.7, 3.2, 3.8 రాశుల యొక్క మధ్యగతము ఎంత ?
సాధన.
3. 3, 3. 5, 3. 1, 3.7, 3.2, 3.8 ల ఆరోహణ క్రమం
= 3.1, 3.2, 3.3, 3.5, 3.7, 3.8
n = 6 (సరిసంఖ్య)
కావున మధ్యగతం = \(\frac{n}{2},\left(\frac{n}{2}+1\right)\) ల సరాసరి
= \(\frac{6}{2},\left(\frac{6}{2}+1\right)\)
= 3, 4 రాశుల సరాసరి
= \(\frac{3.3+3.5}{2}\)
= \(\frac {6.8}{2}\)
= 3.4

ప్రశ్న13.
ఆరోహణ క్రమములోనున్న రాశులు .10, -12, 14, x – 3, x, x + 2, 25 ల మధ్యగతము 15 అయిన x విలువ ఎంత ?
సాధన.
ఇచ్చిన రాశులు 10, 12, 14, x – 3, x, x + 2, 25
⇒ n = 7 (బేసి సంఖ్య)
∴ మధ్యగతం = \(\frac{\mathrm{n}+1}{2}=\frac{7+1}{2}\) = 4వ పదం
= x – 3
⇒ x – 3 = 15
x = 15 + 3
∴ x = 18

ప్రశ్న14.
10, 12, 11, 10, 15, 20, 19, 21, 11, 9, 10 రాశుల యొక్క బాహుళకము ఎంత ?
సాధన.
ఇచ్చిన రాశులు : 10, 12, 11, 10, 15, 20, 19, 21, 11, 9, 10
పై రాశులలో అత్యధికంగా పునరావృతమయ్యే సంఖ్య 10.
∴ బాహుళకం = 10

ప్రశ్న15.
కొన్ని రాశుల బాహుళకము x, దత్తాంశములోని అన్ని రాశుల నుండి 3 తీసివేయగా, కొత్త దత్తాంశమునకు బాహుళకము ఎంత ?
సాధన.
కొన్ని రాశుల బాహుళకం = x
దత్తాంశంలోని అన్ని రాశుల నుండి 3 తీసివేసిన వచ్చు బాహుళకం = x – 3

ప్రశ్న16.
1 నుండి 100 వరకు సహజ సంఖ్యలను వ్రాయుటలో ఉపయోగించు అంకెలన్నింటి యొక్క బాహుళకము ఎంత ?
సాధన.
1 నుండి 100 వరకు గల అంకెలు
1, 2, 3, …….. 99, 100 వరకు గల సహజ సంఖ్యల బాహుళకం = 0
ఒక్కొక్క సంఖ్య యొక్క బాహుళకం = 1
(∵ ఒక్కొక్క సంఖ్య ఒకసారి మాత్రమే వస్తుంది)

ప్రశ్న17.
ఒక దత్తాంశములోని రాశులు 5, 28, 15, 10, 15, 8, 24. నాలుగు రాశులను కలుపగా దత్తాంశము యొక్క సరాసరి, మధ్యగతములో మార్పులేదు కానీ బాహుళకము 1 పెరిగినది. అయిన కలిపిన 4 సంఖ్యలేవి ?
సాధన.
ఇచ్చిన రాశులు 5, 28, 15, 10, 15, 8, 24
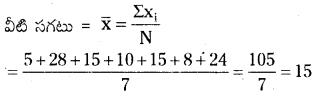
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 11
మధ్యగతం = 5, 8, 10, 15, 15, 24, 28 (n = 7)
= \(\frac{\mathrm{n}+1}{2}=\frac{7+1}{2}\) = 4 వ రాశి = 15
బాహుళకం = 15
దత్తాంశానికి కలుపవలసిన 4 రాశులు x₁, x₂, x₃, x₄ అనుకొనుము.
బాహుళకం ‘1’ పెరిగినది. అనగా 3 సంఖ్యలు సమానాలు అని అర్థం.
∴ x₁ = x₂ = x₃ = x అనుకొనుము.
∴ 5, 8, 10, 15, 15, 24, 28, x, x, x, x₄ యొక్క సగటు
⇒ \(\frac{x+x+x+x_{4}+105}{11}\) = 15
⇒ 3x + x₄ = 165 – 105 = 60
3x + x₄ = 60 ——— (1)
5, 8, 10, 15, 15, 24, 28, x, x, x, x₄ యొక్క బాహుళకం = x అగును.
కానీ లెక్క ప్రకారం 4 సంఖ్యలను కొత్తగా కలుపగా ఏర్పడు బాహుళకం ‘1’ పెరిగినచో
∴ x = 15 + 1 = 16 అగును.
∴ x = 16 ——- (2)
(1), (2) ల నుండి
∴ 3x + x₄ = 60 ⇒ x₄ = 60 – 48
∴ x₄ = 12
∴ కావలసిన సంఖ్యలు వరుసగా x, x, x, x₄ = 16, 16, 16, 12 అగును.

ప్రశ్న18.
x₁, x₂, ……., ……. x₁₀ రాశుల సరాసరి 20 అయిన x₁ + 4, x₂ + 8, x₃ + 12, ….., X₁₀ + 40 రాశుల సరాసరి కనుగొనుము.
సాధన.
x₁, x₂, ………… x₁₀ రాశుల సరాసరి
\(\frac{\Sigma \mathrm{x}_{10}}{\mathrm{~N}}\) = 20 ……. (1)
x₁ + 4, x₂ + 8, x₃ + 12, …… x₁₀ + 40 ల సరాసరి
= \(\frac{x_{1}+4+x_{2}+8+\ldots \ldots . x_{10}+40}{N}\)
AP Board 8th Class Maths Solutions Chapter 7 పౌనఃపున్య విభాజన పట్టికలు, రేఖాచిత్రములు Ex 7.1 12

ప్రశ్న19.
9 పూర్ణసంఖ్యల జాబితాలో 6 పూర్ణసంఖ్యలు 7, 8, 3, 5, 9 మరియు 5 లు అయిన ఆ 9 పూర్ణసంఖ్యలకు గల గరిష్ఠ మధ్యగతము కనుగొనండి.
సాధన.
9 పూర్ణసంఖ్యలలో ఇచ్చిన 6 పూర్ణసంఖ్యలు
7, 8, 3, 5, 9, 5
వీటి ఆరోహణ క్రమం
⇒ 3, 5, 5, 7, 8, 9
మిగిలిన 3 పూర్ణసంఖ్యలు x₁, x₂, x₃ లు అనుకొనుము.
∴ 3, 5, 5, 7, 8, 9, x₁, x₂, x₃ ల మధ్యగతం
= \(\frac{\mathrm{n}+1}{2}\) (n = 9 ఒక బేసి సంఖ్య)
\(\frac{9+1}{2}\) = 5 వ రాశి = 8
∴ ఇచ్చిన రాశుల గరిష్ఠ మధ్యగతం = 8

ప్రశ్న20.
9 వేర్వేరు రాశుల మధ్యగతము 20. అందుగల నాలుగు మిక్కిలి పెద్ద సంఖ్యలకు ప్రతి రాశికి 2 కలపగా వచ్చు కొత్త రాశుల మధ్యగతము కనుగొనండి.
సాధన.
9 రాశులు x₁ < x₂ < x₃ < x₄ < x₅ < x₆ < x₇ < x₈ < x₉ అనుకొనుము.
వీటి మధ్యగతం = \(\frac{\mathrm{n}+1}{2}\) [n = 9 ఒక బేసి సంఖ్య ]
\(\frac{9+1}{2}\) = 5 వ రాశి = x₅ = 20
∴ x₅ = 20
చివరి 4 పెద్ద రాశులకు ప్రతి సంఖ్యకు 2ను కలుపగా వచ్చు రాశులు x₁, x₂, x₃, x₄, x₅, x₆ + 2, x₇ + 2, x₈ + 2, x₉ + 2 ∴ మధ్యగతం = \(\frac{\mathrm{n}+1}{2}\) (n ఒక బేసి సంఖ్య)
= \(\frac{9+1}{2}\) = 5వ రాశి
∴ x₅ = 20