AP Board 8th Class Maths Solutions Chapter 8 జ్యామితీయ పటాల అన్వేషణ Ex 8.1

SCERT AP 8th Class Maths Solutions Chapter 8 జ్యామితీయ పటాల అన్వేషణ Ex 8.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 8th Lesson జ్యామితీయ పటాల అన్వేషణ Exercise 8.1

ప్రశ్న1.
నిత్యమూ ఉపయోగించే మూడు జతల సర్వసమాన వస్తువులను పేర్కొనండి.
సాధన.
నిత్యం ఉపయోగించే సర్వసమాన వస్తువులు :
i) చెవి రింగుల జత
ii) సైకిల్ చక్రాలు
iii) భుజాల పొడవులు సమానంగా గల రెండు చతురస్రాకార కేకులు

ప్రశ్న2.
a) రెండు సర్వసమాన పటాలను గీయండి. అవి సరూపాలవుతాయా ? వివరించండి.
b) రెండు సరూప పటాలను’ తీసుకోండి. వాటిని జరిపినా, భ్రమణం చెందించినా లేదా త్రిప్పిన అవి సరూపాలుగానే ఉంటాయా ?
సాధన.
a) ∴ ΔABC ≅ ΔPQR

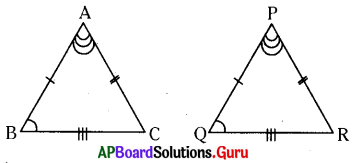
∴ ΔAB = PQ
AC = PR
BC = QR
∠A = ∠P
∠B = ∠Q
∠C = ∠R
∴ సర్వసమాన త్రిభుజాలు సరూపాలు అగును. కాని సరూప త్రిభుజాలు సర్వసమాన త్రిభుజాలు కావు.

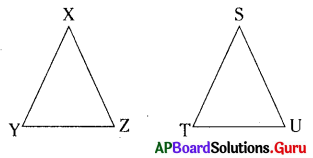
∴ ΔXYZ ~ ΔSTU ల నుండి ఇవి సరూప పటాలు వీటిని భ్రమణం చెందించిన అవి మరలా సరూపాలు గానే ఉంటాయి. (∵ సరూపకత స్థిరత్వం).

ప్రశ్న3.
ΔABC ≅ ΔNMO అయిన అనురూప భుజాలను, అనురూప కోణాల జతలను తెల్పండి.
సాధన.

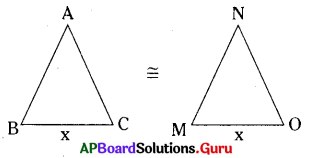
ΔABC ≅ ΔNMO సర్వసమాన త్రిభుజాల నుండి
AB = NM
BC = MO
AC = NO
∠A = ∠N
∠B = ∠M
∠C = ∠O

ప్రశ్న4.
క్రింది ప్రవచనాలు సత్యమవుతాయో, లేదో తెల్పండి. కారణాలను వివరించండి.
i) 3 సెం.మీ. భుజాలుగా గల రెండు చతురస్రాలలో ఒకదానిని 45° మేర భ్రమణం చెందించిన, అవి సర్వసమానాలు.
ii) 5 సెం.మీ. కర్ణాలుగా గల రెండు లంబకోణ త్రిభుజాలు సర్వసమానాలు.
iii) 4 సెం.మీ. వ్యాసార్థంగా గల రెండు వృత్తాలు సర్వసమానాలు.
iv) 4 సెం.మీ. భుజంగా గల రెండు సమబాహు – త్రిభుజాలు ΔABC మరియు ΔLHN లు సర్వసమానాలు కావు.
v) ఒక బహుభుజి మరియు దాని ప్రతిబింబములు సర్వసమానాలు.
సాధన.
i) సత్యం, ఒక చతురస్రాన్ని 45° మేర భ్రమణం చెందించిన అది మొదటి చతురస్రం వలె ఉండును. అపుడు అవి సర్వసమానాలు అగును.
ii) సత్యం, రెండు లంబకోణ త్రిభుజాల కర్ణాలు సమానమైన వాని అనురూప భుజాలు, కోణాలు కూడా సమానంగా ఉండును.
∴ రెండు త్రిభుజాలు సర్వసమానంగా ఉండును.

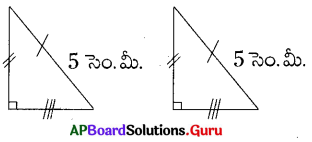
iii) సత్యం, రెండు వృత్త వ్యా సార్ధాలు (r1 = r2 = 4cm) సమానమైన అవి సర్వసమానాలు.
iv) అసత్యం.

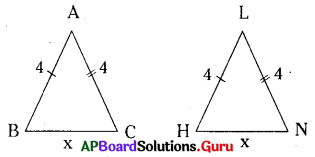
ఒక త్రిభుజంలోని రెండు భుజాలు రెండవ త్రిభుజంలోని రెండు అనురూప భుజాలకు సమానమైన మూడవ భుజాలు కూడా అనుపాతంలో ఉంటాయి.
∴ ΔABC ≅ Δ LHN
కాని ΔABC ≠ ΔLHN అని ఇచ్చారు. కావునా ఇది అసత్యం .
v) సత్యం
ఒక బహుభుజి మరియు దాని ప్రతిబింబాలు ఒకదానికొకటి ఏకీభవిస్తాయి కావునా అవి సర్వసమానాలు.

ప్రశ్న5.
ఒక చతురస్ర బిందు మాపనిపై బహుభుజిని ఒకదానిని గీయండి. మరియు దాని వివిధ దిశలలో సర్వసమాన పటాలు మరియు ప్రతిబింబ పటాన్ని గీయండి.
సాధన.

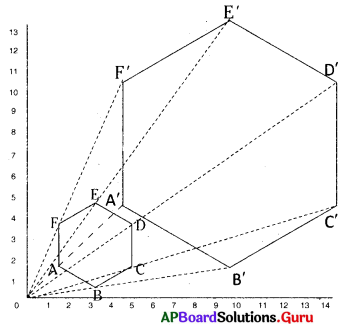
∴ ABCDEF ~ A’B’C’D’E’F’

ప్రశ్న6.
ఒక గ్రాఫ్ కాగితంపై లేదా చతురస్ర బిందు మాపనిపై ఒక దీర్ఘచతురస్రాన్ని గీయండి. దానికి సరూప పటాన్ని నిర్మించండి. ఈ రెండు పటాల వైశాల్యాలు మరియు చుట్టుకొలతలు కనుగొని వాటి వాటి నిష్పత్తులను దీర్ఘచతురస్రాల భుజాల నిష్పత్తులతో పోల్చండి.
సాధన.

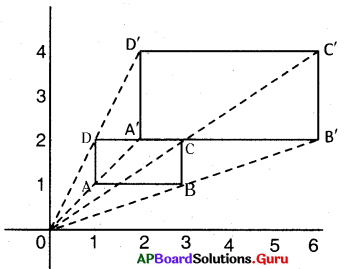
ప్రశ్న7.
ఒక ఇనుప కమ్మీ 7 స్థంభాలపై పటంలో చూపినట్లుగా ఉంచబడింది. ఏ రెండు స్థంభాల మధ్య దూరమైనా 1 మీ.కి సమానం మరియు చివరి స్థంభం ఎత్తు 10.5 మీ. అయిన అన్ని స్థంభాల ఎత్తులను కనుగొనండి.

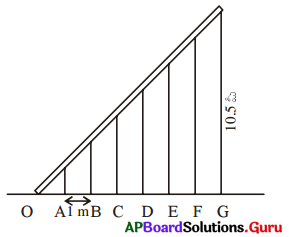
సాధన.

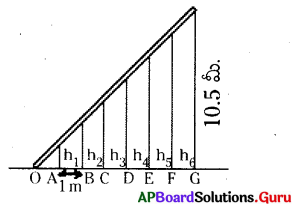
మొదటి స్థంభం ఎత్తు h₁ = \(\frac {1}{7}\) × 10.5 = 1.5 మీ.
2వ స్థంభం ఎత్తు h₂ = \(\frac {2}{7}\) × 10.5 = 3 మీ.
3వ స్తంభం ఎత్తు h₃ = \(\frac {3}{7}\) × 10.5 = 4.5 మీ.
4వ స్తంభం ఎత్తు h₄ = \(\frac {4}{7}\) × 10.5 = 6 మీ.
5వ స్థంభం ఎత్తు h₅ = \(\frac {5}{7}\) × 10.5 = 7.5 మీ.
6వ స్థంభం ఎత్తు h₆ = \(\frac {6}{7}\) × 10.5 = 9 మీ.

ప్రశ్న8.
3 మీ. ఎత్తుగల ఒక నిలువు స్థంభం నుండి 5 మీ. దూరంలో నిలబడి, సుధ, ఒక భవనం పైభాగము మరియు స్థంభం పైభాగం ఒకే సరళరేఖలో ఉన్నట్లు గమనించినది. భవనం మరియు స్థంభాల మధ్య దూరం 10 మీ. అయిన భవనం ఎత్తు అంచనా వేయుము. (సుధ ఎత్తును లెక్కలోనికి తీసుకోకుండా)
సాధన.
ΔOAD ~ ΔOCD
రెండు సరూప త్రిభుజాల
అనురూప భుజాలు
అనుపాతంలో ఉంటాయి.

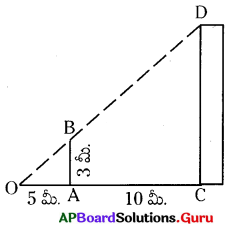
∴ \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{AB}}{\mathrm{CD}}\)
⇒ \(\frac{5}{15}=\frac{3}{h}\)
⇒ \(\frac{1}{3}=\frac{3}{h}\)
⇒ h = 3 × 3 = 9
h = భవనం ఎత్తు = 9 మీ.

ప్రశ్న9.
ఏదేని ఒక చతుర్భుజాన్ని గీయండి. సూచీ భిన్నం 3 ఉండునట్లు దాని విస్తరణ పటాన్ని గీయండి. వాటి అనురూప భుజాలను కొలిచి ఆ రెండు పటాలు సరూపాలేమో సరిచూడండి.
సాధన.

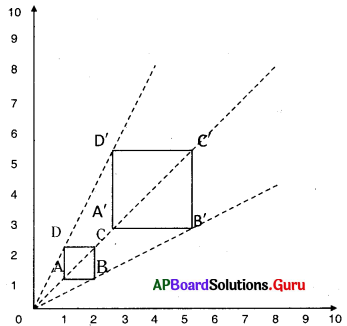
పై పటం నుండి ☐ ABCD ఒక చతుర్భుజం గ్రాఫ్ కాగితం పై గీయబడినది.
అన్ని శీర్షాలు A B C D లు 0 నుండి కలుపబడి వాటికి మూడు రెట్ల దూరాలు వరుసగా A’B’C’D’ లకు కలుపగా ☐ ABCD కు 3 రెట్లు కొలతలు గల చతుర్భుజాన్ని ఏర్పరచినవి.
ఇక్కడ ‘0’ ను విస్తరణ కేంద్రం అని
మరియు = \(\frac{\mathrm{OA}^{\prime}}{\mathrm{OA}}=\frac{3}{1}\) = 3 ను సూచీ భిన్నం అని అంటారు.
∴ □ ABCD ~ □ A’B’C’D’
(∵ వాని అనురూప భుజాలు సమానాలు)
\(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CD}}{\mathrm{C}^{\prime} \mathrm{D}^{\prime}}=\frac{\mathrm{DA}}{\mathrm{D}^{\prime} \mathrm{A}^{\prime}}\)