AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.4

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.4

Question 1.
Simple the following expressions.
i) (5 + √7) (2 + √5)
Solution:
(5 + √7) (2 + √5)
= 10 + 5√5 + 2√7 + √35

ii) (5 + √5) (5 – √5)
Solution:
(5 + √5) (5 – √5)
= 5² + (√5)²
= 25 – 5 = 20

(iii) (√3 + √7)²
Solution:
(√3 + √7)²
= (√3)² + (√7)² + 2(√3)(√7)
= 3 + 7 + 2√21
= 10 + 2√21

iv) (√11 – √7) (√11 + √7)
= (√11)² – (√7)²
= 11 – 7 = 4

Question 2.
Classify the following numbers as rational or irrational.
i) 5 – √3
ii) √3 + √2
iii) (√2 – 2)²
iv) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
v) 2π
vii) (2 +√2) (2 – √2)
Solution:
i) 5 – √3 – irrational
ii) √3 + √2 – irrational
iii) (√2 – 2)² – irrational
iv) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\) – rational
v) 2π – Transcendental number. (not irrational)
vi) \(\frac{1}{\sqrt{3}}\)– irrational
vii) (2 +√2) (2 – √2) – rational

Question 3.
In the following equations, find whether variables x, y, z etc., represents rational or irrational numbers.
i) x² = 7
ii) y² = 16
iii) z² = 0.02
iv) u² = \(\frac{17}{4}\)
v) w² = 27
vi) t⁴ = 256
Solution:
i) x² = 7
⇒ x = √7 is an irrational number.
ii) y² = 16 ⇒ y = 4 is a rational number.
iii) z² = 0.02 ⇒ z = \(\sqrt{0.02}\) is an irrational number.
iv) u² = \(\frac{17}{4}\) ⇒ x = \(\frac{\sqrt{17}}{2}\) is an irrational number.
v) w² = 27 ⇒ w = \(3 \sqrt{3}\) an irrational number.
vi) t⁴ = 256 ⇒ t² = \(\sqrt{256}\) = 16
⇒ t = \(\sqrt{16}\) = 4 is a rational number

Qeustion 4.
The ratio of circumference to the diameter of a circle c/d is represented by π. But we say that π is an irrational number. Why?

Question 5.
Rationalise the denominators of the following.
i) \(\frac{1}{3+\sqrt{2}}\)
Solution:

ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
Solution:

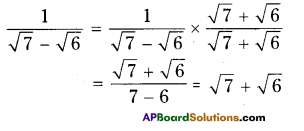
iii) \(\frac{1}{\sqrt{7}}\)
Solution:

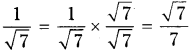
iv) \(\frac{\sqrt{6}}{\sqrt{3}-\sqrt{2}}\)
Solution:

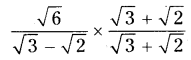
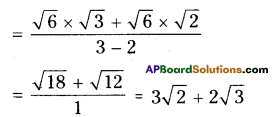
Question 6.
Simplify each of the following by rationalising the denominator.
i) \(\frac{6-4 \sqrt{2}}{6+4 \sqrt{2}}\)
Solution:

ii) \(\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}\)
Solution:

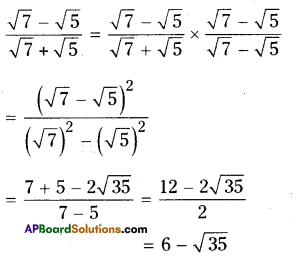
iii) \(\frac{1}{3 \sqrt{2}-2 \sqrt{3}}\)
Solution:

iv) \(\frac{3 \sqrt{5}-\sqrt{7}}{3 \sqrt{3}+\sqrt{2}}\)
Solution:

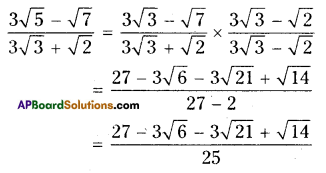
Question 7.
Find the value of \(\frac{\sqrt{10}-\sqrt{5}}{2 \sqrt{2}}\) upto three decimal places. (take \(\sqrt{2}\) = 1.414, \(\sqrt{3}\) = 1.732 and \(\sqrt{5}\) = 2.236).
Solution:

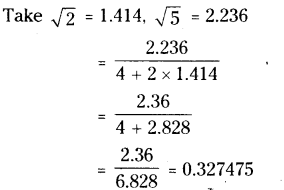
Question 8.
Find
i) 64^1/6
Solution:
= (2⁶)^1/6
= 6

ii) 32^1/5
Solution:
32^1/5
= (2⁵)^1/5
= 2

iii) 625^1/4
625^1/5
= (5⁴)^1/4
= 5

iv) 16^3/2
Solution:
16^3/2
= (4²)^3/2

v) 243^2/5
Solution:
243^2/5
= (3⁵)^2/5

vi) (46656)^-1/6
Solution:

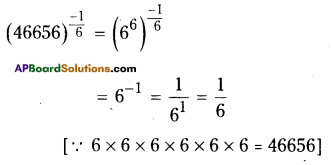
Question 9.
Simplify \(\sqrt[4]{81}-8 \sqrt[3]{343}+15 \sqrt[5]{32}+\sqrt{225}\)
Solution:

Question 10.
If ‘a’ and ‘b’ are rational numbers, find the values of a and b in each of the following equations.
i) \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\mathbf{a}+\mathbf{b} \sqrt{6}\)
Solution:
Given that \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\mathbf{a}+\mathbf{b} \sqrt{6}\)
Rationalising the denominator we get

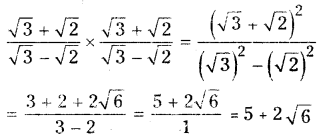
Comparing 5 + 2√6 with a + b√6
We have a = 5 and b = 2

ii) \(\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}=a-b \sqrt{15}\)
Solution:
Given that \(\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}=a-b \sqrt{15}\)
Rationalising the denominator we get

AP Board 9th Class Maths Solutions