AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.5

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.5 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.5

Question 1.
Use suitable identities to find the following products.
i) (x + 5) (x + 2)
Solution:
(x + 5) (x + 2)
= x² + (5 + 2)x + 5 x 2
[ ∵ (x + a) (x + b) = x² + (a + b) x + ab]
= x² + 7x + 10

ii) (x – 5) (x – 5)
Solution:
(x – 5) (x – 5)
= (x – 5)² = x² – 2(x) (5) + 5²
[ ∵(x – y)² = x² – 2xy + y²]
= x² – 10x + 25

iii) (3x + 2) (3x – 2)
Solution:
(3x + 2) (3x – 2) = (3x)² – (2)²
[∵ (x + y) (x – y) =x² – y²]
= 9x² – 4

iv) \(\left(x^{2}+\frac{1}{x^{2}}\right)\left(x^{2}-\frac{1}{x^{2}}\right)\)
Solution:

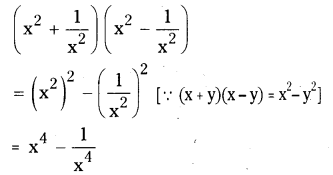
v) (1 + x) (1 + x)
Solution:
(1 + x) (1 + x)
= (1 + x)² = 1² + 2 (1) (x) + x²
[∵(x + y)² = x² + 2xy + y²]
= 1 + 2x + x²

Question 2.
Evaluate the following products with¬out actual multiplication.
i) 101 x 99
Solution:
101 x 99
= (100 + 1) (100 – 1)
= 100² – 1²
= 10000 – 1
= 9999

ii) 999 x 999
Solution:
999 x 999
= 999²
= (1000 – 1)²
= 1000² – 2 x (1000) x 1 + 1²
= 1000000-2000 + 1
= 998001

iii) \(50 \frac{1}{2} \times 49 \frac{1}{2}\)
Solution:

iv) 501 x 501
Solution:
501 x 501
= (500 + 1) (500 + 1)
= (500 + 1)²
= 500² + 2 x (500) x 1 + 1²
= 250000 + 1000 + 1 = 251001

v) 30.5 x 29.5 = (30 + 0.5) (30 – 0.5)
= 30² – (0.5)²
= 900 – 0.25
= 899.75

Question 3.
Factorise the following using appro-priate identities.
i) 16x² + 24xy + 9y²
Solution:
16x² + 24xy + 9y2
= (4x)² + 2 (4x) (3y) + (3y)²
= (4x + 3y)² = (4x + 3y) (4x + 3y)
[ ∵ (x + y)² = x² + 2xy + y²]

ii) 4y² – 4y + 1
Solution:
4y² – 4y + 1
= (2y)² – 2 (2y) (1) + (1)²
[ ∵ (x -y)² = x² – 2xy + y²]
= (2y -1)² = (2y – 1) (2y-1)

iii) \(4 x^{2}-\frac{y^{2}}{25}\)
Solution:

iv) 18a² – 50
Solution:
18a² – 50 = 2 (9a² – 25)
= 2[(3a)² – (5)²]
[ ∵ x² – y² = (x + y) (x – y)]
= 2 (3a + 5) (3a – 5)

v) x² + 5x + 6
Solution:
x² + 5x + 6 = x² + (3 + 2) x + 3 x 2
[ ∵ (x + a) (x + b) = x² + (a + b) x + a . b]
= (x + 3) (x + 2)

vi) 3p² – 24p + 36
Solution:
3p² – 24p + 36
= 3[p² – 8p + 12]
= 3[p² + (- 6 – 2)p + (- 6) (- 2)]
[ ∵ (x + a) (x + b) = x² + (a + b) x + ab]
= 3 (p – 6) (p – 2)

Question 4.
Expand each of the following, using suitable identities.
i) (x + 2y + 4z)2
(x + 2y + 4z)² = (x)² + (2y)² + (4z)² + 2(x) (2y) + 2 (2y) (4z) + 2 (4z) (x)
[ ∵ (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx]
= x² + 4y² + 16z² + 4xy + 16yz + 8zx

ii) (2a – 3b)³
Solution:
(2a – 3b)³ = (2a)³ – 3 (2a)² (3b) + 3 (2a) (3b)² – (3b)³
[ ∵ (a – b)³ = a³ – 3a²b + 3ab² – b³]
= 8a³ – 3(4a²) (3b) + 3 (2a) (9b²) – 27b³
= 8a³ – 36a²b + 54ab²-27b³
(or)
∵ (a – b)³ = a³ – b³– 3ab (a – b)]
= (2a)³ – (3b)³ – 3(2a) (3b) (2a – 3b)
= 8a³ – 27b³ – 18ab (2a – 3b)

iii) (- 2a + 5b – 3c)²
Solution:
(- 2a + 5b – 3c)²
= (- 2a)² + (5b)² + (- 3c)² + 2 (- 2a) (5b) + 2 (5b) (- 3c) + 2 (- 3c) (- 2a)
= 4a² + 25b² + 9c² – 20ab – 30bc + 12ca
[ ∵ (x + y + z)² = x² + y² + z² + 2xy +2yz +2za]

iv) \(\left[\frac{a}{4}-\frac{b}{2}+1\right]^{2}\)
Solution:

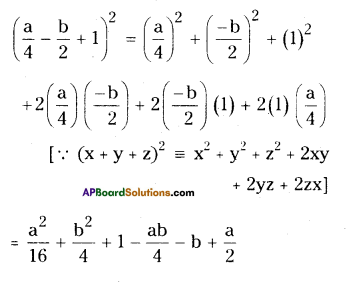
v) (p + 1)³
Solution:
(p + 1)³
= (P)³ + 3 (p)² (1) + 3 (p) (1)² + (1)³
[ ∵ (x + y)³ = x³ + 3x²y + 3xy² + y³]
= p³ + 3p² + 3p + 1

vi) \(\left(x-\frac{2}{3} y\right)^{3}\)
Solution:

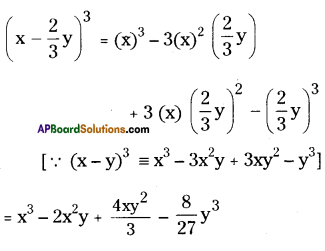
Question 5.
Factorise
i) 25x² + 16y² + 4z² – 40xy + 16yz – 20xz
Solution:
25x² + 16y² + 4z² – 40xy + 16yz – 20xz
= (5x)² + (- 4y)² + (- 2z)² + 2(5x) (- 4y) + 2 (- 4y) (- 2z) + 2 (- 2z) (5x)
= (5x – 4y – 2z)² = (- 5x + 4y +, 2z)²

ii) 9a² + 4b² + 16c² + 12ab – 16bc – 24ca
Solution:
9a² + 4b² + 16c² + 12ab – 16bc -24ca
= (3a)² + (2b)² + (- 4c)²+ 2 (3a) (2b) + 2 (2b) (- 4c) + 2(- 4c) (3a)
= (3a + 2b – 4c)²

Question 6.
If a + b + c = 9 and ab + be + ca = 26, find a² + b² + c².
Solution:
Given that a + b + c = 9
Squaring on both sides,
(a + b + c)² = 9²
⇒ a²+ b² + c²+ 2 (ab + be + ca) = 81 ⇒ a² + b² + c² = 81 – 2 (ab + be + ca)
(by problem)
= 81 – 2 x 26
= 81 – 52 = 29

Question 7.
Evaluate the following by using suit¬able identities. m EachgM)
i) (99)³
Solution:
(99)² = (100 – 1)³
= 100³ – 3 (100)² (1) + 3 (100) (1)² – 1³
[ ∵ (x – y)³ = x³ – 3x²y + 3xy² + y³]
= 1000000 – 30000 + 300 – 1
= 970299

ii) (102)³
Solution:
(102)³ = (100 + 2)³
= 100³ + 3 (100)² (2) + 3 (100) (2)² + 2³
[ ∵ (x + y)³ = x³ + 3x²y + 3xy² + y³]
= 1000000 + 60000 + 1200 + 8
= 1061208

iii) (998)³
Solution:
(998)³ =(1000 – 2)³
[ ∵ (x – y)³ = x³ – 3x²y + 3xy² – y³] = 1000³– 3(1000)²(2) + 3(1000)(2)²– 2³
= 1000000000 – 6000000 + 12000 – 8
= 994011992

iv) (1001)³
Solution:
(1001)³ = (1000 + 1)³ .
[ ∵ (x + y)³ = x³ + 3x²y + 3xy² + y³] = 1000³ + 3(1000)²(1) + 3(1000) (1)² + 1³
= 1000000000 + 3000000 + 3000 + 1
= 1003003001

Question 8.
Factorise each of the following.
i) 8a³ + b³ + 12a² b + 6ab²
Solution:
8a³ + b³ + 12a² b + 6ab²
= (2a)³ + (b)³ + 3 (2a)² (b) + 3 (2a) (b)²
= (2a + b)³

ii) 8a³ – b³ – 12a² b + 6ab²
Solution:
8a³ – b³ – 12a² b + 6ab²
= (2a)³ – (b)³ – 3 (2a)² (b) + 3 (2a) (b)²
= (2a – b)³

iii) 1 – 64a³ -12a + 48a²
Solution:
1 – 64a³ – 12a + 48a²
= (1)³ – (4a)³ – 3(1)² (4a) + 3(1) (4a)²
= (1 – 4a)³

iv) \(8 p^{3}-\frac{12}{5} p^{2}+\frac{6}{25} p-\frac{1}{125}\)
Solution:

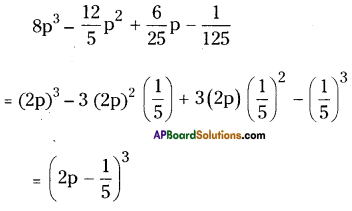
Question 9.
Verify i) x³ + y³ = (x + y) (x² – xy + y²);
ii) x³ – y³ = (x – y) (x² + xy + y²)
Using some non-zero positive integers and check by actual multiplication. Can you
call these as identities ?
i) x³ + y³ = (x + y) (x² – xy + y²)
Solution:
Given x³ + y³ = (x + y) (x² – xy + y²)
L.H.S = x³ + y³
R.H.S = (x + y) (x² – xy + y²)
= x (x² – xy + y²) + y (x² – xy + y²)
= x³ -x²y + xy² + x²y – xy² + y³
= x³ + y³
= L.H.S
∴ L.H.S = R.H.S

Take x = 3, y = 2
L.H.S = 3³ + 2³ = 27 + 8 = 35
R.H.S = (3 + 2) (3² – 3 x 2 + 2²)
= 5 x (9 – 6 + 4)
= 5 x 7 = 35
∴ L.H.S = R.H.S

ii) x³ – y³ = (x – y) (x² + xy + y²)
Solution:
Given that x³ – y³ = (x – y) (x² + xy + y²)
L.H.S = x³ – y³
R.H.S = (x – y) (x² + xy + y²)
= x (x² + xy + y²) – y (x² + xy + y²)
= x³ + x²y + xy² – x²y – xy² – y³
= x³ – y³= L.H.S

L.H.S = 3³ – 2³ = 27 – 8 = 19
R.H.S = (3 – 2) (3² + 3 x 2 + 2²)
= 1 x (9 + 6 + 4)
= 1 x 19 = 19
∴ L.H.S = R.H.S
We can call the above two expressions as identities

Question 10.
Factorise by using the above results (identities).
i) 27a³ + 64b³
Solution:
27a³+ 64b³ = (3a)³ + (4b)³
= (3a + 4b) {(3a)² – (3a) (4b) + (4b)²}
= (3a + 4b) (9a² – 12ab + 16b²)

ii) 343y³ – 1000
Solution:
343y³ – 1000 = (7y)³ – (10)³
= (7y – 10) [(7y)² + (7y) (10) + (10)²]
= (7y – 10) (49y² + 70y + 100)

Question 11.
Factorise 27x³ + y³ + z³ – 9xyz using identity.
Solution:
Given 27x³ + y³ + z³ – 9xyz
= (3x)³ + (y)³ + (z)³ – 3 (3x) (y) (z)
= (3x + y + z)
[(3x)² + y² + z² – (3x) (y) – (y) (z) – (z) (3x)]
[ ∵ (x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z²– xy – yz – zx)
= (3x + y + z) (9x² + y² + z² – 3xy – yz – 3xz)

Question 12.
Verify that x³+ y³ + z³ – 3xyz = 1/2 (x + y + z) [(x – y)² + (y – z)² + (z – x)² ]
(OR)
Verify that
p³ + q³ + r³ – 3pqr = 1/2 (p + q + r)
[(p – q)² + (q – r)² + (r – p)²]
Solution:
Given x³+ y³ + z³ – 3xyz = 1/2 (x + y + z) [(x – y)² + (y – z)² + (z – x)² ]
R-H.S = 1/2 (x + y + z) [(x – y)² + (y – z)²+ (z – x)²]
= 1/2 (x + y + z) [x² + y² – 2xy + y² + z² – 2yz + z² + x² – 2xz]
= 1/2 (x + y + z) [2x² + 2y² + 2z² – 2xy – 2yz – 2zx]
= 1/2 (x + y + z) (2) [x² + y² + z² – xy – yz – zx]
= (x + y + z) (x² + y² + z² – xy – yz – zx)
= L.H.S
Hence proved.

Question 13.
If x + y + z = 0, show that x³ + y³ + z³ = 3xyz
Solution:
Given x + y + z = 0
To prove x³ + y³ + z³ = 3xyz
We have an identity
(x + y + z) (x² + y² + z² – xy – yz – zx)
= x³ + y³ + z³ – 3xyz
Substituting x + y + z = 0in the above equation, we get
0 x (x² + y² + z² -xy-yz-zx)
= x³ + y³ + z³ – 3xyz
⇒ x³ + y³ + z³ – 3xyz = 0
⇒ x³ + y³ + z³ = 3xyz

Question 14.
Without actual calculating the cubes, find the value of each of the following.
i) (- 10)³ + 7³ + 3³
Solution:
Given (-10)³ + 7³ + 3³
Sum of the bases = -10 + 7 + 3 = = 0
∴ (- 10)³ + 7³ + 3³
= 3 (- 10) x (7) x 3
= -630
[ ∵ x + y + z = 0 then x³ + y³ + z³ = 3xyz]

ii) (28)³ + (- 15)³ + (- 13)³
Solution:
Given (28)³ + (- 15)³+ (- 13)³
Sum of the bases = 28 + (- 15) + (- 13) = 0
∴ (28)³ + (- 15)³ + (- 13)³
= 3 x 28 x (- 15) x (- 13)
= 16380

iii) \(\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{3}\right)^{3}-\left(\frac{5}{6}\right)^{3}\) read it as \(\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{3}\right)^{3}+\left(\frac{-5}{6}\right)^{3}\)
Solution:

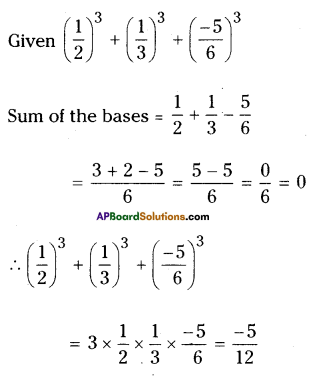
iv) (0.2)³ – (0.3)³ + (0.1)³
Solution:
Given that (0.2)³ – (0.3)³ + (0.1)³
= (0.2)³ + (- 0.3)³ + (0.1)³
Sum of the bases = 0.2 – 0.3 + 0.1 = 0
∴ (0.2)³ + (-0.3)³ + (0.1)³
= 3 x (0.2) (- 0.3) (0.1)
= -0.018

Question 15.
Give possible expressions for the length and breadth of the rectangle whose area is given by
i) 4a² + 4a – 3
Given that area = 4a² + 4a – 3
= 4a² + 6a – 2a – 3
= 2a (2a + 3) – 1 (2a + 3)
= (2a – 1) (2a + 3)
∴ Length = (2a + 3); breadth = (2a – 1).

ii) 25a² – 35a + 12
Solution:
Given that area = 25a² – 35a +12
= 25a² – 20a – 15a + 12
= 5a (5a – 4) – 3 (5a – 4)
= (5a – 4) (5a – 3)
∴ (5a – 4) (5a – 3) are the length and breadth.

Question 16.
What are the possible polynomial expressions for the dimensions of the cuboids whose volumes are given below ?
i) 3x³ – 12x
Solution:
Volume = 3x³ – 12x
= 3x (x² – 4)
= 3x (x + 2) (x – 2) are the dimensions.

ii) 12y² + 8y – 20
Solution:
Given that volume = 12y² + 8y – 20
= 4 (3y² + 2y – 5)
= 4 [3y² + 5y – 3y – 5]
= 4 [y (3y + 5) – 1 (3y + 5)]
= 4 (3y + 5) (y – 1)
Hence 4, (3y + 5) and (y – 1) are the dimensions.

Question 17.
Show that if 2 (a² + b² ) = (a + b)² then a = b
Solution:
Given that 2 (a² + b² ) = (a + b)²
To prove a = b
As 2 (a² + b² ) = (a + b)²
We have
2a² + 2b² = a² + 2ab + b²
2a² – a² + 2b² – b² = 2ab
a² + b² = 2ab
This is possible only when a = b
∴ a = b