AP State Syllabus AP Board 9th Class Maths Solutions Chapter 8 Quadrilaterals Ex 8.4 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 8th Lesson Quadrilaterals Exercise 8.4
Question 1.
ABC is a triangle. D is a point on AB such that AD = \(\frac { 1 }{ 4 }\) AB and E is a point on AC such that AE = \(\frac { 1 }{ 4 }\) AC. If DE = 2 cm find BC.
Solution:
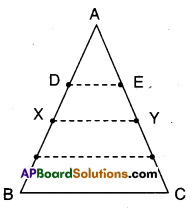
Given that D and E are points on AB and AC.
Such that AD = \(\frac { 1 }{ 4 }\) AB and AE = \(\frac { 1 }{ 4 }\) AC
Let X, Y be midpoints of AB and AC.
Joint D, E and X, Y.
Now in ΔAXY; D, E are the midpoints of sides AX and AY.
∴ DE // XY and DE = \(\frac { 1 }{ 2 }\) XY
⇒ 2 cm = \(\frac { 1 }{2 }\) XY
⇒ XY = 2 x 2 = 4cm
Also in ΔABC; X, Y are the midpoints of AB and AC.
∴ XY//BC and XY = \(\frac { 1 }{2 }\) BC
4 cm = \(\frac { 1 }{2 }\) BC
⇒ BC = 4 x 2 = 8 cm
![]()
Question 2.
ABCD is a quadrilateral. E, F, G and H are the midpoints of AB, BC, CD and DA respectively. Prove that EFGH is a parallelogram.
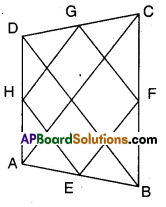
Solution:
Given that E, F, G and H are the midpoints of the sides of quad. ABCD.
In ΔABC; E, F are the midpoints of the sides AB and BC.
∴ EF//AC and EF = \(\frac { 1 }{2 }\) AC
Also in ΔACD; HG // AC
and HG = \(\frac { 1 }{ 2 }\) AC
∴ EF // HG and EF = HG
Now in □EFGH; EF = HG and EF // HG
∴ □EFGH is a parallelogram.
![]()
Question 3.
Show that the figure formed by joining the midpoints of sides of a rhom¬bus successively is a rectangle.
Solution:
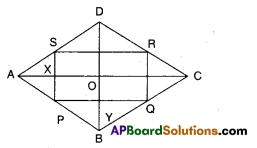
Let □ABCD be a rhombus.
P, Q, R and S be the midpoints of sides of □ABCD
In ΔABC,
P, Q are the midpoints of AB and BC.
∴ PQ//AC and PQ = \(\frac { 1 }{2 }\)AC …………………..(1)
Also in ΔADC, ,
S, R are the midpoints of AD and CD.
∴ SR//AC and SR = \(\frac { 1 }{2 }\)AC ………………(2)
From (1) and (2);
PQ // SR and PQ = SR
Similarly QR // PS and QR = PS
∴ □PQRS is a parallelogram.
As the diagonals of a rhombus bisect at right angles.
∠AOB – 90°
∴ ∠P = ∠AOB = 90°
[opp. angles of //gm PYOX] Hence □PQRS is a rectangle as both pairs of opp. sides are equal and parallel, one angle being 90°.
![]()
Question 4.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.
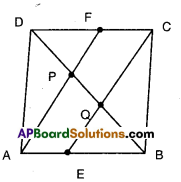
Solution:
□ABCD is a parallelogram. E and F are the mid points of AB and CD.
∴ AE = \(\frac { 1 }{2 }\)AB and CF = \(\frac { 1 }{2 }\)CD
Thus AE = CF [∵ AB – CD]
Now in □AECF, AE = CF and AE ||CF
Thus □AECF is a parallelogram.
Now in ΔEQB and ΔFDP
EB = FD [Half of equal sides of a //gm]
∠EBQ = ∠FDP[alt. int.angles of EB//FD]
∠QEB = ∠PFD
[∵∠QED = ∠QCF = ∠PFD]
∴ ΔEQB ≅ ΔFPD [A.S.A. congruence]
∴ BQ = DP [CPCT] ……………… (1)
Now in ΔDQC; PF // QC and F is the midpoint of DC.
Hence P must be the midpoint of DQ
Thus DP = PQ …………….. (2)
From (1) and (2), DP = PQ = QB
Hence AF and CE trisect the diagonal BD.
![]()
Question 5.
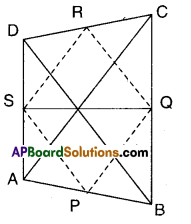
Show that the line segments joining the mid points of the opposite sides of a quadrilateral and bisect each other.
Solution:
Let ABCD be a quadrilateral.
P, Q, R, S are the midpoints of sides of □ABCD.
Join (P, Q), (Q, R), (R, S) and (S, P).
In ΔABC; P, Q are the midpoints of AB and BC.
∴ PQ // AC and PQ = \(\frac { 1 }{2 }\)AC ………….(1)
Also from ΔADC
S, R are the midpoints of AD and CD
SR // AC and SR = \(\frac { 1 }{2 }\) AC …………………(2)
∴ From (1) & (2)
PQ = SR and PQ //SR
∴ □PQRS is a parallelogram.
Now PR and QS are the diagonals of □ PQRS.
∴ PR and QS bisect each other.
![]()
Question 6.
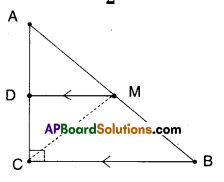
ABC is a triangle right angled at’C’. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that
i) D is the midpoint of AC
ii) MD ⊥ AC
iii) CM = MA= \(\frac { 1 }{2 }\)AB
Solution:
Given that in ΔABC; ∠C = 90°
M is the midpoint of AB.
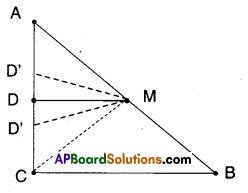
i) If ‘D’ is the midpoints of AC.
The proof is trivial.
Let us suppose D is not the mid point of AC.
Then there exists D’ such that AD’ = D’C
Then D’M is a line parallel to BC through M.
Also DM is a line parallel to BC through M.
There exist two lines parallel to same line through a point M.
This is a contradiction.
There exists only one line parallel to a given line through a point not on the line.
∴ D’ must coincides with D
∴ D is the midpoint of AC
ii) From (i) DM // BC
Thus ∠ADM = ∠ACB = 90°
[corresponding angles]
⇒ MD ⊥ AC
![]()
iii) In ∆ADM and ∆CDM
AD = CD [ ∵ D is midpoint from (i)]
∠ADM = ∠MDC (∵ 90° each)
DM = DM (Common side)
∴ ∆ADM = ∆CDM (SAS congruence)
⇒ CM = MA (CPCT)
CM = \(\frac { 1 }{2 }\) AB (∵ M is the midpoint of AB)
∴ CM = MA = \(\frac { 1 }{2 }\)AB