AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 1 ప్రమేయాలు Exercise 1(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Exercise 1(a)

Question 1.
f(x) = \(\left\{\begin{array}{l}
x+2, x>1 \\
2,-1 \leq x \leq 1 \\
x-1,-3<x<-1 \end{array}\right.\) గా నిర్వచిస్తే, కింది విలువలు కనుక్కోండి.
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(-2)
(v) f(-5)
Solution:
(i) f(3)
x > 1, f(x) = x + 2
∴ f(3) = 3 + 2 = 5

(ii) f(0)
-1 ≤ x ≤ 1, f(x) = 2
∴ f(0) = 2

(iii) f(-1.5)
-3 < x < -1, f(x) = x – 1
∴ f(-1.5) = -1.5 – 1 = 2.5

(iv) f(2) + f(-2)
x > 1, f(x) = x + 2
∴ f(2) = 2 + 2 = 4
-3 < x < -1, f(x) = x – 1
∴ f(-2) = -2 – 1 = -3
∴ f(2) + f(-2) = 4 + (-3) = 1

(v) f(-5)
f ప్రదేశం {x/x ∈ (-3, ∞)} కనుక f(-5) నిర్వచితం కాదు.

Question 2.
f: R – (0) → R ను f(x) = \(x^3-\frac{1}{x^3}\) గా నిర్వచిస్తే, f(x) + f(\(\frac{1}{x}\)) = 0 అని చూపండి.
Solution:
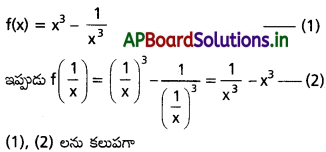
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) I Q2

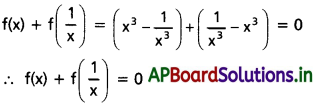
Question 3.
f: R → R ను f(x) = \(\frac{1-x^2}{1+x^2}\), గా నిర్వచిస్తే, f(tan θ) = cos 2θ అని చూపండి.
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) I Q3

Question 4.
f : R – {±1} → R f(x) = \(\log \left|\frac{1+x}{1-x}\right|\) గా నిర్వచిస్తే, \(f\left(\frac{2 x}{1+x^2}\right)\) = 2 f(x) అని చూపండి.
Solution:
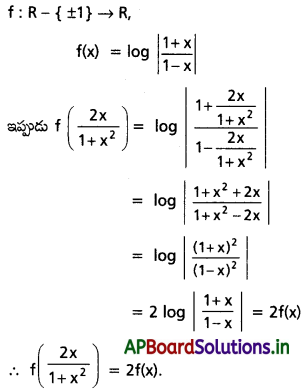
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) I Q4

Question 5.
A = {-2, -1, 0, 1, 2), అయితే f : A → B సంగ్రస్త ప్రమేయం f(x) = x² + x + 1 గా నిర్వచిస్తే, B కనుక్కోండి.
Solution:
A = {-2, -1, 0, 1, 2}
f: A → B, f(x) = x² + x + 1
f : A → B సంగ్రస్త ప్రమేయం కనుక
f(-2) = (-2)² + (-2) + 1 = 4 – 2 + 1 = 3
f(-1) = (-1)² + (-1) + 1 = 1 – 1 + 1 = 1
f(0) = 0² + 0 + 1 = 0 + 0 + 1 = 1
f(1) = 1² + 1 + 1 = 1 + 1 + 1 = 3
f(2) = 2² + 2 + 1 = 4 + 2 + 1 = 7
∴ B = f(A) = {3, 1, 7}

Question 6.
A = {1, 2, 3, 4}, అయితే f : A → R ను f(x) = \(\frac{x^2-x+1}{x+1}\) గా నిర్వచిస్తే f వ్యాప్తి కనుక్కోండి.
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) I Q6

Question 7.
f(x + y) = f(xy) ∀ x, y అయితే f స్థిరప్రమేయం అని చూపండి.
Solution:
f(x + y) = f(xy), x, y ∈ R
x = y = 0 అనుకొంటే
⇒ f(0) = f(0) …….(1)
అప్పుడు x = 1, y = 0
⇒ f(1) = f(0) …….(2)
Let x = 1, y = 1
f(2) = f(1) …….(3)
(1) ,(2), (3) నుండి
f(0) = f(1) = f(2)
⇒ f(0) = f(2)
⇒ f(3) = f(0)
⇒ f(4) = f (0)
.
.
.
f(n) = f(0)
∴ f అనునది స్థిర ప్రమేయము.

II.

Question 1.
A = {x/-1 ≤ x ≤ 1}, f(x) = x², g(x) = x³, గా నిర్వచిస్తే, కింది ప్రమేయాలలో ఏవి సంగ్రస్తాలు?
(i) f : A → A
(ii) g : A → A
Solution:
(i) f : A → A
∵ A = {x/-1 ≤ x ≤ 1], f(x) = x²
⇒ f(x) అనేది A నుంచి A కు ప్రమేయం
(i.e.,) f : A → A
y ∈ A అనుకొందాం.
f(x) = y అయ్యేటట్లుగా x² = y అవుతుంది.
⇒ x = √y
y = -1 అయితే x = √-1 ∉ A
కనుక f : A → A సంగ్రస్త ప్రమేయం కాదు.

(ii) g : A → A
∵ A = {x/-1 ≤ x ≤ 1], g(x) = x³
⇒ g : A → A
y ∈ A అనుకొందాం.
అప్పుడు g(x) = y
⇒ x³ = y
⇒ x = \(y^{1 / 3}\) ∈ A
y = -1 అయితే x = -1 ∈ A
y = 0 అయితే x = 0 ∈ A
y = 1 అయితే x = 1 ∈ A
∴ g : A → A సంగ్రస్త ప్రమేయం.

Question 2.
కింది వాటిలో ఏవి సంగ్రస్తం, అన్వేకం, ద్విగుణం అవుతాయో నిర్ణయించండి.
(i) f : R → R ను f(x) = \(\frac{2 x+1}{3}\) గా నిర్వచించాం. [Mar. ’15]
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) II Q2(i)

(ii) f : R → (0, ∞) ను f(x) = 2^x గా నిర్వచించాం.
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) II Q2(ii)

(iii) f : (0, ∞) → R ను f(x) = log_ex గా నిర్వచించాం.
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) II Q2(iii)

(iv) f : [0, ∞) → [0, ∞) ను f(x) = x² గా నిర్వచించాం.
Solution:
x₁, x₂ ∈ [0, ∞) (i.e.,) f ప్రదేశం .
f(x₁) = f(x₂)
⇒ \(\mathrm{x}_1^2=\mathrm{x}_2^2\)
⇒ x₁ = x₂ [∵ x₁, x₂ ≥ 0]
∴ f(x) = x², f : {0, ∞) → {0, ∞) అన్వేకం
y ∈ (0, ∞), (సహ ప్రదేశం) కు
y = x²
⇒ x = √y, [∵y ≥ 0]
అప్పుడు f(x) = x²
= (√y)²
= y
∴ f : (0, ∞) → (0, ∞) సంగ్రస్తం
∴ f ద్విగుణ ప్రమేయం

(v) f : R → [0, ∞) ను f(x) = x² గా నిర్వచించాం.
Solution:
x₁, x₂ ∈ R.
f(x₁) = f(x₂)
⇒ \(\mathrm{x}_1^2=\mathrm{x}_2^2\)
⇒ x₁ = ±x₂, [∵ x₁, x₂ ∈ R]
f అన్వేకం కాదు.
y ∈ [0, ∞)
y = x²
⇒ x = √y, y ∈ [0, ∞)
అప్పుడు f(x) = x²
= (√y)²
= y
∴ f : R → (0, ∞) సంగ్రస్తం కనుక f ద్విగుణ ప్రమేయం కాదు.

(vi) f : R → R ను f(x) = x² గా నిర్వచించాం.
Solution:
x₁, x₂ ∈ R, (f ప్రదేశం)
∴ f(x₁) = f(x₂)
⇒ \(\mathrm{x}_1^2=\mathrm{x}_2^2\)
⇒ x₁ = ±x₂, [∵ x₁, x₂ ∈ R]
∴ f(x) అన్వేకం కాదు.
(-∞, 0) సహప్రదేశంలో ఉన్న మూలకానికి పూర్వబింబం లేదు. కనుక f సంగ్రస్తం కాదు.
∴ f ద్విగుణ ప్రమేయం కాదు.

Question 3.
g = {(1, 1), (2, 3), (3, 5), (4, 7)}. ఇది A = {1, 2, 3, 4} నుంచి B = {1, 3, 5, 7} ప్రమేయం అవుతుందా? g(x) = ax + b గా నిర్వచిస్తే, a, b విలువలు కనుక్కోండి.
Solution:
A = {1, 2, 3, 4}; B = {1, 3, 5, 7}
g = {(1, 1), (2, 3), (3, 5), (4, 7)}
కనుక g(1) = 1, g(2) = 3, g(3) = 5, g(4) = 7
A లో ప్రతీ a ∈ A కి అనురూపంగా (a, b) ∈ g అయ్యేటట్లు B లో ఒకే ఒక్క b వ్యవస్థితం అవుతుంది.
కనుక g : A → B ప్రమేయం అవుతుంది.
ఇప్పుడు g(x) = ax + b,
g(1) = a(1) + b = 1
⇒ a + b = 1 ……(1)
g(2) = a(2) + b
⇒ 2a + b = 3 …….(2)
(1), (2) ను సాధించగా a = 2, b = -1.

Question 4.
f : R → R ను f(x) = \(\frac{3^x+3^{-x}}{2}\) గా నిర్వచిస్తే, f(x + y) + f(x – y) = 2 f(x) f(y) అని చూపండి.
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) II Q4

Question 5.
f : R → R ను f(x) = \(\frac{4^x}{4^x+2}\) గా నిర్వచిస్తే f(1 – x) = 1 – f(x) అని చూపండి. f(1/4) + 2f(1/2) + f(3/4) విలువ రాబట్టండి.
Solution:
f : R → R, f(x) = \(\frac{4^x}{4^x+2}\)
ఇప్పుడు f(1 – x) = \(\frac{4^{1-x}}{4^{1-x}+2}\)
AP Inter 1st Year Maths 1A Solutions Chapter 1 ప్రమేయాలు Ex 1(a) II Q5

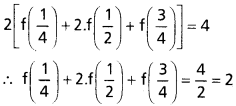
Question 6.
f : (-1, 1) → (0, 2) ను f(x) = ax + b గా నిర్వచించిన ప్రమేయం సంగ్రస్తమయితే a, b విలువలు కనుక్కోండి.
Solution:
f : {-1, 1} → {0, 2}, f(x) = ax + b సంగ్రస్తం కనుక
f(-1) = 0, f(1) = 2 (or) f(-1) = 2, f(1) = 0
సందర్భం (i) f(-1) = 0, f(1) = 2
∴ a(-1) + b = 0 ⇒ a + b = 0 ……..(1)
a(1) + b = 2 ⇒ a + b = 2 ………(2)
(1), (2) ల నుండి a = 1, b = 1
సందర్భం (ii) f(-1) = 2, f(1) = 0
a(-1) + b = 2 ⇒ -a + b = 2 ……..(3)
a(1) + b = 0 ⇒ a + b = 0 ………(4)
(3), (4) ల నుండి a = -1, b = 1
∴ a = ±1, b = 1

Question 7.
f(x) = cos(log x) అయితే \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]\) = 0 అని చూపండి.
Solution:
f(x) = cos (log x)
\(f\left(\frac{1}{x}\right)=\cos \left(\log \left(\frac{1}{x}\right)\right)\)
= cos (log 1 – log x)
= cos (-log x)
= cos (log x)
ఇదే విధంగా
f(\(\frac{1}{y}\)) = cos (log y)
f(\(\frac{x}{y}\)) = cos log (\(\frac{x}{y}\))
= cos (log x – log y)
f(xy) = cos log(xy)
= cos (log x + log y)
f(\(\frac{x}{y}\)) + f(xy) = cos (log x – log y) + cos (log x + log y)
= 2 cos (log x) cos (log y)
∴ cos (A – B) + cos (A + B) = 2 cos A . cos B
LHS = \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]\)
= cos (log x) cos (log y) – \(\frac{1}{2}\) [2 cos (log x) cos (log y)]
= 0