AP Inter 1st Year Maths 1B Solutions Chapter 4 సరళరేఖాయుగ్మాలు Ex 4(b)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 4 సరళరేఖాయుగ్మాలు Exercise 4(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 4 సరళరేఖాయుగ్మాలు Exercise 4(b)

అభ్యాసం – 4 (బి)

I.

ప్రశ్న 1.
2x² + xy – 6y² + 7y – 2 = 0 లు సూచించే సరళ రేఖల మధ్యకోణం కనుక్కోండి.
సాధన:
దత్త సమీకరణము 2x² + xy – 6y² + 7y – 2 = 0
2x² + xy – 6y² = 2x² + 4xy – 3xy – 6y²
= 2x (x + 2y) – 3y (x + 2y)
= (2x – 3y) (x + 2y)
2x² + xy – 6y² + 7y – 2 = 0 = (2x – 3y + c₁) (x + 2y + c₂)
x గుణకాలు సమానం చేస్తే c₁ + 2 = 0
y గుణకాలు సమానం చేస్తే 2c₁ – 3c₂ = 7
సాధించగా c₁ = 2, c₂ = -1
సరళరేఖల సమీకరణాలు 2x – 3y + 2 = 0, x + 2y – 1 = 0

ప్రశ్న 2.
2x² + 3xy – 2y² + 3x + y + 1 = 0 సమీకరణం ఒక లంబరేఖాయుగ్మాన్ని సూచిస్తుందని నిరూపించండి.
సాధన:
a = 2, f = 1/2
b = -2 , g = 3/2
c = 1, h = 3/2
abc + 2fgh – af² – bg² – ch²
= 2(-2)(1) + 2.\(\frac{1}{2}\) . \(\frac{31}{2}\) . \(\frac{3}{2}\) – 2 . \(\frac{1}{4}\) + 2 . \(\frac{9}{4}\) – 1 \(\frac{9}{4}\)
= -4 + \(\frac{9}{4}\) – \(\frac{1}{2}\) + \(\frac{18}{4}\) – \(\frac{9}{4}\)
= -4 + \(\frac{9}{4}\) – \(\frac{1}{2}\) + \(\frac{9}{2}\) – \(\frac{9}{4}\)
= 0
h² – ab = \(\frac{9}{4}\) + 4 = \(\frac{25}{4}\) > 0,
g² – ac = \(\frac{9}{4}\) – 2 = \(\frac{1}{4}\) > 0,
f² – bc = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
a + b = 2 – 2 = 0 దత్తరేఖలు లంబంగా ఉన్నాయి.

II.

ప్రశ్న 1.
3x² + 7xy + 2y² + 5x + 5y + 2 సమీకరణం ఒక సరళరేఖాయుగ్నాన్ని సూచిస్తుందని నిరూపించి, ఆ సరళరేఖల ఖండన బిందువును కనుక్కోండి
సాధన:
3x² + 7xy +2y² + 5x + 5y + 2 = 0
పోల్చగా a= 3 ; 2f = 5 ⇒ f = \(\frac{5}{2}\)
b = 2 ; 2g = 5 ⇒ g = \(\frac{5}{2}\)
c = 2 ; 2h = 7 ⇒ h = \(\frac{7}{2}\)
∆ = abc + 2fgh – af² – bg² – ch²
= 3(2) (2) + 2 . \(\frac{5}{2}\) . \(\frac{5}{2}\) . \(\frac{7}{2}\)– 3 . \(\frac{25}{4}\) – 2 . \(\frac{25}{4}\) – 2 . \(\frac{49}{4}\)
= \(\frac{1}{2}\) (48 + 175 – 75 – 50 – 98)
= \(\frac{1}{2}\) (223 – 223) = 0
h² – ab = \(\left(\frac{7}{2}\right)^2\) – 2.6 = \(\frac{49}{4}\) – 12 = \(\frac{1}{4}\) > 0
f² – bc = \(\left(\frac{5}{2}\right)^2\) – 2.2 = \(\frac{25}{4}\) – 4 = \(\frac{9}{4}\) > 0
g² – ac = \(\left(\frac{5}{2}\right)^2\) – 3.2 = \(\frac{25}{4}\) – 6 = \(\frac{1}{4}\) > 0
∴ దత్త సమీకరణము రేఖాయుగ్మాన్ని సూచించే ఖండన బిందువు

ప్రశ్న 2.
2x² + kxy – 6y² + 3x + y + 1 = 0 సమీకరణం ఒక సరళరేఖాయుగ్మాన్ని సూచిస్తే K విలువ కనుక్కోండి. K యొక్క ఆ విలువకు ఆ సరళరేఖల ఖండన బిందువును, వాటి మధ్యకోణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణము
2x² + kxy – 6y² + 3x + y + 1 = 0
a = 2. ; 2f = 1 ⇒ f = \(\frac{1}{2}\)
b = -6 ; 2g = 3 ⇒ g = \(\frac{3}{2}\)
c = 1 ; 2h = k ⇒ h = \(\frac{k}{2}\)
దత్త సమీకరణము రేఖాయుగ్మాన్ని సూచిస్తే
abc + 2fgh – af² – bg² – ch² = 0
-12 + 2 . \(\frac{1}{2}\) . \(\frac{3}{2}\) . (+\(\frac{k}{2}\)) – 2 . \(\frac{1}{4}\) + 6 . \(\frac{9}{4}\) – \(\frac{k^2}{4}\) = 0
-48 + 3k – 2 + 54 – k² = 0
-k² + 3k + 4 = 0 ⇒ k² – 3k – 4 = 0
(k – 4) (k + 1) = 0
k = 4 లేదా. – 1.
సందర్భం i) : k = -1
ఖండన బిందువు

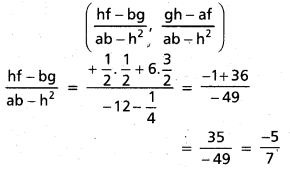
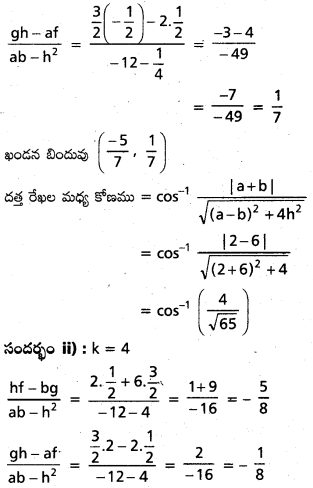
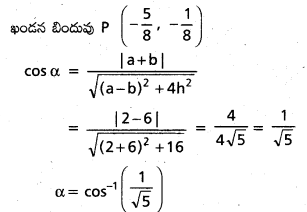
ప్రశ్న 3.
x² – y² – x + 3y – 2 0 సమీకరణం రెండు లంబరేఖలను సూచిస్తుందని నిరూపించి, వాటి సమీకరణాలను కనుక్కోండి.
సాధన:
పోల్చగా a = 1 ; f = \(\frac{3}{2}\)
b = -1 ; g = –\(\frac{1}{2}\)
c = -2 ; h = 0
abc + 2fgh – af² – bg² – ch²
= 1 (-1) (-2) + 0 – 1 . \(\frac{9}{4}\) + 1 . \(\frac{1}{4}\) + 0
= +2 – \(\frac{9}{4}\) + \(\frac{1}{4}\) = 0
h² – ab = 0 – 1 (-1) = 1 > 0,
f² – bc = \(\frac{9}{4}\) – 2 = \(\frac{1}{4}\) > 0
g² – ac = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
a + b = 1 – 1 = 0
దత్త సమీకరణము లంబరేఖా యుగ్మాన్ని సూచిస్తుంది.
x² – y² – x + 3y – 2 = (x + y + c₁) (x – y + c₂)
x గుణకాలు సమానం చేయగా,
⇒ c₁ + c₂ = -1
y గుణకాలు సమానం చేయగా,
⇒ -c₁ + c₂ = 3
కూడగా 2c₂ = 2 ⇒ c₂ = 1
c₁ + c₂ = 1 ⇒ c₁ + 1 = -1
c₁ = -2
రేఖల సమీకరణాలు x + y – 2 = 0 మరియు x – y + 1 = 0

ప్రశ్న 4.
x² + 2xy – 35y² – 4x + 44y – 12 = 0 సూచించే రేఖాయుగ్మం 5x + 2y – 8 = 0 అనే సరళరేఖ అనుషక్తాలవుతాయని చూపండి.
సాధన:
దత్త రేఖల సమీకరణాలు
x² + 2xy – 35y² – 4x + 44y – 12 = 0
a = 1 ; f = 22
b = -35 ; g = -2
c = – 12 ; h = 1

P బిందువు 5x + 2y – 8 = 0 రేఖ మీద ఉంది.
∴ దత్త రేఖలు అనుషక్తాలు.

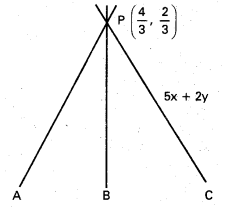
ప్రశ్న 5.
క్రింద ఇచ్చిన సమాంతర రేఖాయుగ్మాల మధ్య దూరాలను కనుక్కోండి.
i) 9x² – 6xy + y² + 18x – 6y + 8 = 0
సాధన:
సమాంతర రేఖల మధ్య దూరం = 2\(\sqrt{\frac{g^2-a c}{a(a+b)}}\)
= \(2 \sqrt{\frac{9^2-9.8}{9(9+1)}}=2 \sqrt{\frac{9}{9.10}}\)
= \(\sqrt{\frac{4}{10}}=\sqrt{\frac{2}{5}}\)

ii) x² + 2\(\sqrt{3}\)xy + 3y² – 3x – 3\(\sqrt{3}\)y – 4 = 0
సాధన:
సమాంతర రేఖల మధ్య దూరం = 2\(\sqrt{\frac{g^2-a c}{a(a+b)}}\)
= \(2 \sqrt{\frac{\frac{9}{4}+4}{1(1+3)}}=2 \sqrt{\frac{25}{4.4}}=\frac{5}{2}\)

ప్రశ్న 6.
3x² + 8xy – 3y² = 0, 3x² + 8xy – 3y² + 2x – 4y – 1 = 0 అనే రేఖాయుగ్మాలతో ఒక చతురస్రం ఏర్పడుతుందని నిరూపించండి.

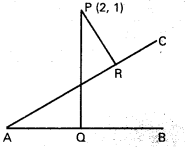
సాధన:
OA, OB ల ఉమ్మడి సమీకరణాలు
3x² + 8xy – 3y²
(x + 3y) (3x – y) = 0
3x – y = 0, x + 3y = 0
OA సమీకరణము 3x – y = 0 ……………….. (1)
OB సమీకరణము x + 3y = 0 ………………. (2)
CA, CB ల ఉమ్మడి సమీకరణాలు
3x² + 8xy – 3y² + 2x – 4y + 1 = 0
3x² + 8xy – 3y² + 2x – 4y + 1 = (3x – y + c₁)(x + 3y + c₂)
x గుణకాలను సమానం చేయగా c₁ + 3c₂ = 2
y గుణకాలను సమానం చేయగా 3c₁ + c₂ = – 4

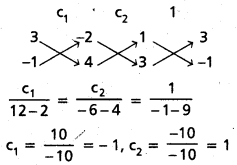
BC సమీకరణం 3x – y – 1 = 0 ……………… (3)
AC సమీకరణం x + 3y + 1 = 0 ……………… (4)
OA, BC లు సమీకరణాలు స్థిరపదాలలో మాత్రమే చేధిస్తున్నా
⇒ OA, BC లు సమాంతరాలు
OB, CA లు సమీకరణాలు స్థిరపదాలలో మాత్రమే చేధిస్తున్నా
⇒ OB, AC లు సమాంతరాలు
OA, OB ల ఉమ్మడి సమీకరణము.
a + b = 3 – 3 = 0, OACB దీర్ఘచతురస్రం.
OA = 0నుండి AC మీదకు లంబదూరము
= \(\frac{|0+0+1|}{\sqrt{1+9}}=\frac{1}{\sqrt{10}}\)
OB = 0 నుండి BC మీదకు లంబదూరము
= \(\frac{|0+0-1|}{\sqrt{9+1}}=\frac{1}{\sqrt{10}}\)
OA = OB మరియు OACB దీర్ఘచతురస్రం
OACB చతురస్రం.

III.

ప్రశ్న 1.
(2, 1) బిందువు నుంచి 12x² + 25xy + 12y² 10x + 11y + 2 = 0 సూచించే సరళరేఖలకు ఉన్న లంబ. దూరాల లబ్దం కనుక్కోండి.

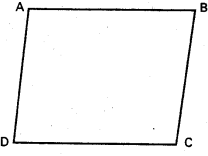
సాధన:
AB, AC ల ఉమ్మడి సమీకరణాలు
12x² + 25xy + 12y² + 10x + 11y + 2 = 0
12x² + 25xy + 12y²
= 12x² + 16xy + 9xy + 12y² = 0
= 4x (3x+4y) + 3y (3x+4y)
= (3x + 4y) (4x + 3y)
12x² + 25xy + 12y² + 10x + 11y + 2
= (3x + 4y + c₁) (4x + 3y + c₂)
x గుణకాలను సమానం చేయగా,
4c₁ +3c₂ = 10 ……………. (1)
y గుణకాలను సమానం చేయగా,
3c₁ + 4c₂ = 11 ……………… (2)
i.e., 4c₁ + 3c₂ – 10 = 0
3c₁ + 4c₂ – 11 = 0

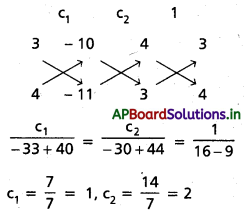
AB సమీకరణం 3x + 4y + 1 = 0
AC సమీకరణం 4x + 3y + 2 = 0
PQ = P నుండి AB మీదకు లంబదూరము
AB = \(\frac{6+4+1}{\sqrt{9+16}}=\frac{11}{5}\)
PR = P నుండి AC మీదకు లంబదూరము
AC = \(\frac{|8+3+2|}{\sqrt{16+9}}=\frac{13}{5}\)
లంబదూరాల లబ్దము
= PQ × PR = \(\frac{11}{5}\) × \(\frac{13}{5}\) = \(\frac{143}{25}\)

ప్రశ్న 2.
y² – 4y + 3 = 0, x² + 4xy + 4y² + 5x + 10y + 4 = 0 అనే సరళరేఖాయుగ్మాలతో ఒక సమాంతర చతుర్భుజం ఏర్పడుతుందని నిరూపించి, దాని భుజాల పొడవులను కనుక్కోండి.

సాధన:
మొదటి రేఖాయుగ్మం సమీకరణం y² – 4y + 3 = 0
(y – 1) (y – 3) = 0
y – 1 = 0 లేదా y – 3 = 0
AB సమీకరణం y – 1 = 0 …………… (1)
CD సమీకరణం y – 3 = 0 ……………. (2)
AB, CDల సమీకరణాలలో స్థిరపదంలో మాత్రమే తేడా ఉంది.
∴ AB, CD లు సమాంతరాలు.
రెండవ రేఖా యుగ్మం సమీకరణం
x² + 4xy + 4y² + 5x + 10y + 4 = 0
(x + 2y)² + 5(x + 2y ) + 4 = 0
(x + 2y)² + 4 (x + 2y) + (x + 2y) + 4 = 0
(x + 2y)(x + 2y + 4) + 1 (x + 2y + 4) = 0
(x + 2y + 1) (x + 2y + 4) = 0
x + 2 y + 1 = 0, x + 2 y + 4 = 0
AD సమీకరణం x + 2y + 1 = 0 ……………… (3)
BC సమీకరణం x + 2 y + 4 = 0 …………….. (4)
AD, BC లు సమాంతరాలు.
(1); (3) లను సాధించగా x + 2 + 1 = 0
x = -3
A నిరూపకాలు (-3, 1)
x = 3
(2), (3) లను సాధించగా x + 6 + 1 = = 0
x = -7
D నిరూపకాలు (-7, 3)
(1), (4) లను సాధించగా x + 2 + 4 = 0
x = – 6
B నిరూపకాలు (−6, 1)
AB = \(\sqrt{(-3+6)^2+(1-1)^2}\)
= \(\sqrt{9+0}\)
= 3
AD = \(\sqrt{(-3+7)^2+(1-3)^2}\)
= \(\sqrt{16+4}\)
= \(\sqrt{20}=2 \sqrt{5}\)
సమాంతర చతుర్భుజ భుజాల పొడవులు 3, \(2 \sqrt{5}\).

ప్రశ్న 3.
ax² + 2hxy + by² + 2gx + 2fy + c = 0 అనే సమీకరణం రేఖాయుగ్మాన్ని సూచిస్తే, మూలబిందువు నుంచి ఈ సరళరేఖలకు ఉన్న దూరాల లబ్ధం \(\frac{|c|}{\sqrt{(a-b)^2+4 h^2}}\) అని నిరూపించండి.
సాధన:
ax² + 2hxy + by² + 2gx + 2fy + c = 0
రేఖాయుగ్మాన్ని సూచిస్తుంది.
l₁ x + m₁y + n₁ = 0 ………………… (1)
l₂ x + m₂y + n₂ = 0 ………………. (2)
⇒ ax² + 2hxy + by² + 2gx + 2fy + c
= (l₁ x + m₁y + n₁)(l₂ x + m₂y + n₂)
l₁l₂ = a,
m₁m₂ = b, l₁m₂ + l₂m₁ = 2h,
l₁n₂ + l₂n₁ = 2g,
m₁n₂ + m₂n₁ = 2f,
n₁n₂ = c
మూలబిందువు నుండి (1) కి లంబదూరము = \(\frac{\left|n_1\right|}{\sqrt{l_1^2+m_1^2}}\)
మూలబిందువు నుండి (2) కి లంబదూరము = \(\frac{\left|n_2\right|}{\sqrt{l_2^2+m_2^2}}\)
లంబాల లబ్ధం

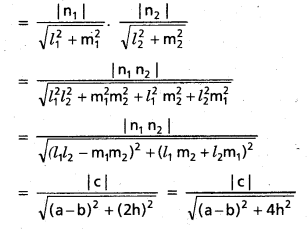
ప్రశ్న 4.
ax² + 2hxy + by² + 2gx + 2fy + c = 0 అనే సమీకరణం ఒక వ్యతిచ్ఛేదక రేఖాయుగ్మాన్ని సూచిస్తే, మూలబిందువు నుంచి వీటి ఖండన బిందువు దూరానికి వర్గం \(\frac{c(a+b)-f^2-g^2}{a b-h^2}\) అవుతుందని చూపండి. దత్త సరళరేఖలు లంబంగా ఉంటే ఈ దూరం యొక్క వర్గం \(\frac{f^2+g^2}{h^2+b^2}\) అని కూడ నిరూపించండి.
సాధన:
ax² + 2hxy + by² + 2gx + 2fy + c = 0
రేఖాయుగ్మాన్ని సూచిస్తుందనుకొందాం.
l₁x + m₁y + n₁ = 0 ……………… (1)
l₂x + m₂y + n₂ = 0 ………………. (2)
(l₁x + m₁y + n₁)(l₂x + m₂y + n₂)
= ax² + 2hxy + by² + 2gx + 2fy + c
l₁l₂ = a, m₁m₂ = b, n₁n₂ = c
l₁m₂ + l₂m₁ = 2h, l₁n₂ + l₂n₁, = 2g,
m₁n₂ + m₂n₁ = 2f
(1); (2) లను సాధించగా