AP Inter 1st Year Maths 1B Solutions Chapter 9 అవకలనం Ex 9(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 9 అవకలనం Exercise 9(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 9 అవకలనం Exercise 9(a)

అభ్యాసం – 9 (ఎ)

I. క్రింది ప్రమేయాలకు అవకలజాలను కనుక్కోండి.

i) \(\sqrt{x}\) + \(2 x^{\frac{3}{4}}\) + \(3 x^{\frac{5}{6}}\) (x > 0)
సాధన:
y = \(\sqrt{x}\) + \(2 x^{\frac{3}{4}}\) + \(3 x^{\frac{5}{6}}\) (x > 0)
\(\frac{d y}{d x}\) = \(\frac{1}{2} \cdot x^{-1 / 2}\) + 2. \(\frac{3}{2}\) . x^-1/4 + 3. \(\frac{3}{2}\) . x^-1/6]

ii) \(\sqrt{2 x-3}\) + \(\sqrt{7-3 x}\) (T.S Mar. ’15)
సాధన:

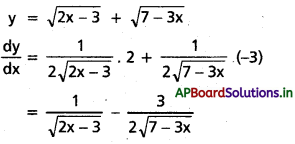
iii) (x² – 3) (4x³ + 1)
సాధన:
y = (x² – 3) (4x³ + 1)
\(\frac{d y}{d x}\) = (x² – 3) – (4x³ + 1)
\(\frac{d y}{d x}\) = (x² – 3) \(\frac{\mathrm{d}}{\mathrm{dx}}\)(4x³ + 1) + (4x³ + 1)\(\frac{\mathrm{d}}{\mathrm{dx}}\)(x² – 3)
= (x² – 3) (12x²) + (4x³ + 1) (2x)
= 12x⁴ – 36x² + 8x⁴ + 2x
= 20x⁴ – 36x² + 2x

iv) (\(\sqrt{x}\) – 3x) (x + \(\frac{1}{x}\))
సాధన:

v) (\(\sqrt{x}\) + 1)(x² – 4x + 2)(x > 0)
సాధన:
y = (\(\sqrt{x}\) + 1) (x² – 4x + 2) (x > 0)
x దృష్ట్యా అవకలనము చేయగా,

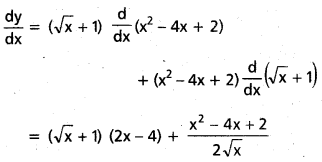
vi) (ax + b)ⁿ (cx + d)^m.
సాధన:

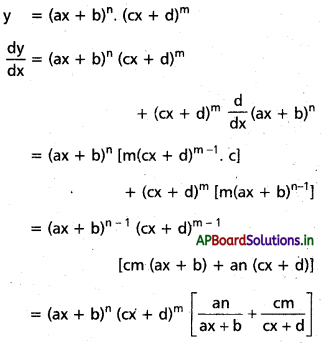
vii) 5 sin x + e^x log.x
సాధన:
y = 5 sin x + e^x. log x
\(\frac{d y}{d x}\) = 5 cos x + e^x. \(\frac{d}{d x}(\log x)\) + log x \(\frac{d}{d x}\left(e^x\right)\)
= 5 cos x + e^x . \(\frac{1}{x}\) + (log x) (e^x)

viii) 5^x + log x + x³ e^x
సాధన:
y = 5x + log x + x³ e^x
\(\frac{d y}{d x}\) = 5^x . log 5 + \(\frac{1}{x}\) + x³.e^x + e^x.3x²
= 5^x.l0g 5 + \(\frac{1}{x}\) + x³ e^x + 3x² e^x

ix) e^x + sin x cos x
సాధన:
y = e^x + sin x. cos x
\(\frac{\mathrm{d} y}{\mathrm{dx}}\) = \(\frac{d}{d x}\)(e^x) + \(\frac{d}{d x}\)(sin x. cos x)
= e^x + sin x \(\frac{\mathrm{d}}{\mathrm{dx}}\) (cos x) + cos x \(\frac{\mathrm{d}}{\mathrm{dx}}\) (sin x)
= e^x – sin² x + cos² x
= e^x + cos 2x

x)
\(\frac{\mathbf{p} x^2+\mathbf{q} x+\mathbf{r}}{\mathbf{a x}+\mathbf{b}}\)(|a| + |b| ≠ 0)
సాధన:

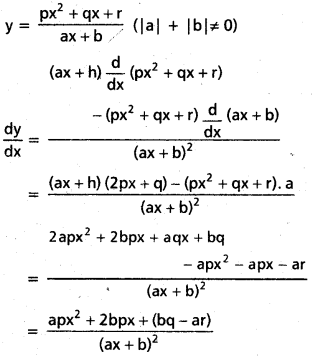
xi) log₇ (log x) (x > 0)
సాధన:
y = log₇ (log x) (x > 0)
\(\frac{d y}{d x}\) = \(\frac{1}{\log _7} \cdot \frac{1}{\log x} \cdot \frac{1}{x}\)
= \(\frac{1}{x(\log x)\left(\log _e^7\right)}\) = \(\frac{\log _7{ }^e}{x \log _e x}\)

xii)
\(\frac{1}{a x^2+b x+c}\) (|a| + |b| + |c| ≠ 0)
సాధన:

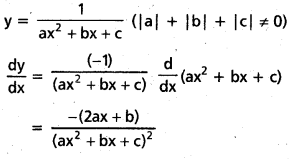
xiii) e^2x log (3x + 4) (x > \(\frac{-4}{3}\)) (May ’13)
సాధన:
y = e^2x. log (3x + 4) (x > –\(\frac{4}{3}\))
x దృష్ట్యా అవకలనము చేయగా,

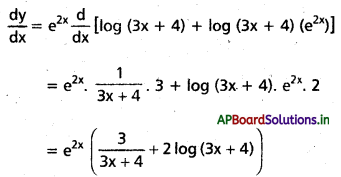
xiv) (4 + x²) e^2x
సాధన:
\(\frac{d y}{d x}\) = (4 + x²) \(\frac{\mathrm{d}}{\mathrm{dx}}\)(e^2x) + e^2x\(\frac{d}{d x}\)(4 + x²)
= (4 + x²). 2e^2x + e^2x (0 + 2x)
= 2e^2x (4 + x² + x]
= 2e^2x (x² + x + 4)

xv) \(\frac{a x+b}{c x+d}\) [|c| + |d| ≠ 0] (May 12)
సాధన:
y = \(\frac{a x+b}{c x+d}\) [|c| + |d| ≠ 0]
x దృష్ట్యా అవకలనము చేయగా

xvi) a^x. e^x2
సాధన:
y = a^x. e^x2
x దృష్ట్యా అవకలనము చేయగా,

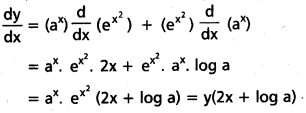
ప్రశ్న 2.
f(x) = 1 + x + x² + …. + x^1oo, అయితే f'(1) విలువ కనుక్కోండి.
సాధన:
f(x) = 1 + 2x + 3x²……… + 100 x⁹⁹
f'(1) = 1 + 2 + 3 …….. + 100
= \(\frac{100 \times 101}{2}\) = 5050 (Σx = \(\frac{x(x+1)}{2}\))

ప్రశ్న 3.
f(x) = 2x² + 3x – 5 అయితే f'(0) + 3f'(-1) = 0 అని చూపండి.
సాధన:
f'(x) = 4x + 3
f'(0) = 0 + 3 = 3
f'(-1) = – 4 + 3 = -1
f(0) + 3f'(-1) 3 + 3(-1) = 3 – 3 = 0

II.

ప్రశ్న 1.
అవకలజం ప్రాథమిక సూత్రం నుంచి కింది ప్రమేయాలు అవకలజాలను కనుక్కోండి. (T.S Mar. ’15)

i) x³
సాధన:

ii) x² + 4
సాధన:
f(x) = x² + 4
f(x + h) – f(x) = ((x + h)⁴ + 4) – (x⁴ + 4)
= ((x + h)⁴ + 4 – x⁴ – 4
= x⁴ + 4x³h + 6x²h² + 4xh³ + h⁴ – x⁴

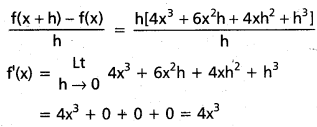
iii) ax² + bx + c
సాధన:
f(x) = ax² + bx + c
f(x + h) = a(x + h)² + b(x + h) + c
= a(x² + 2hx + h²) + b(x + h) + c
= ax² + 2ahx + ah² + bx + bh + c
f(x + h) – f(x) = ax² + 2ahx + ah² + bx + bh + c – ax² – bx – c
= h[2ax + ah + b]

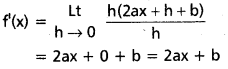
iv) \(\sqrt{x+1}\)
సాధన:

v) sin 2x (May ’13)
సాధన:
f(x) = sin 2x = f(x + h) – f(x)
= sin 2(x + h) – sin 2x
= 2cos \(\frac{2 x+2 h+2 x}{2}\) . sin \(\frac{2 x+2 h-2 x}{2}\)
= 2. cos (2x + h). sin h

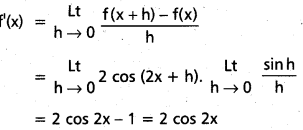
vi) cos ax (Mar. ’13, ’11)
సాధన:

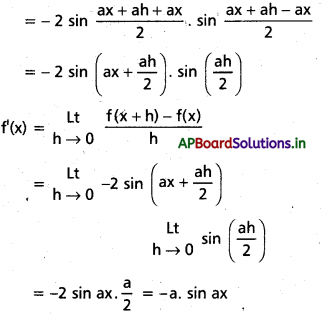
vii) tan 2x
సాధన:

viii) cot x
సాధన:
f(x) = cot x
f(x + h) – f(x) = cot (x + h) – cot x

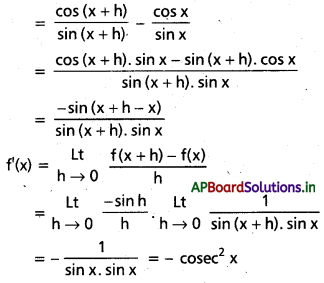
ix) sec 3x
సాధన:
f(x) = sec 3x
f(x + h) − f(x) = sec 3(x + h) – sec 3x

x) x sin x
సాధన:
f(x) = x sin x.
f(x + h) – f(x) = (x + h) sin (x + h) – x sin x
= x (sin (x + h) – sin x) + h. sin (x + h)
= x[2 cos\(\frac{x+h+x}{2}\).sin \(\frac{x+h-x}{2}\)) + h. sin(x + h)

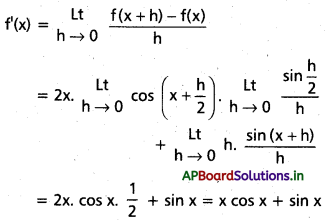
xi) cos² x
సాధన:
f(x) = cos² x
f(x + h) f(x) = cos² (x + h) – cos² x
= -(cos² x – cos² (x + h))
= -sin (x + h + x) sin (x + h – x)

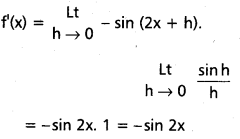
ప్రశ్న 2.
క్రింది ప్రమేయాలకు అవకలజాలను కనుక్కోండి.

i) \(\frac{1-x \sqrt{x}}{1+x \sqrt{x}}\) (x > 0)
సాధన:

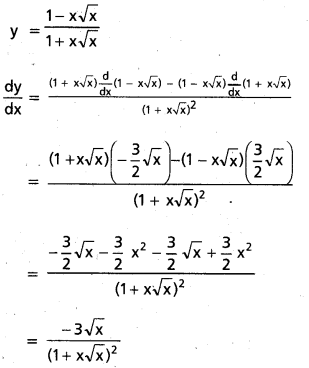
ii) xⁿ. n^x. log (nx) (x > 0, n ∈ N)
సాధన:

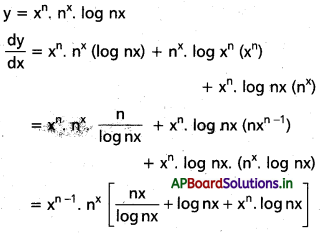
iii) ax²ⁿ. log x + bxⁿ e^-x
సాధన:
y = ax²ⁿ. log x + bxⁿ e^-x

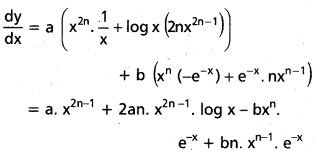
iv) (\(\frac{1}{x}\) – x)³. e^x
సాధన:

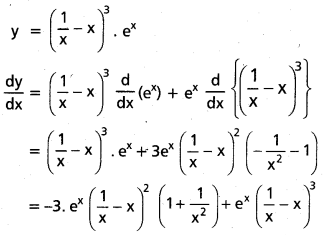
ప్రశ్న 3.
ప్రమేయం f(x) = |x| + |x – 1], x ∈ R, 0, 1ల వద్ద తప్ప అన్ని వాస్తవ సంఖ్యల వద్ద అవకలనీయం అని చూపండి.
సాధన:
f(x) = │x| + |x – 1| ∀ x ∈ R
f(x) = x + x − 1 = 2x − 1, x ≥ 1
= x – (x − 1) = x – x + 1, = 1, 0 < x < 1
= -x – (x – 1) = -x – x + 1 = 1 – 2x, x ≤ 0
∴ f(x) = 2x – 1, x ≥ 1
= 1, 0 < x < 1 = 1 – 2x, x ≤ 0 x > 1, అయితే f(x)= 2x – 1 = x² లో బహుపది
f(x) అన్ని x > 1 లకు అవకలనీయము.
0 < x < 1, అయితే f(x) = 1
∴ f(x), 0 < x < 1 కు అవకలనీయము.
x < 1, అయితే f(x) = 1 – 2x = x లో బహుపది
∴ f(x) అన్ని x < 1 వద్ద అవకలనీయము
సందర్భం i) : x = 0

∴ f'(0) వ్యవస్థితం కాదు.
f(x) అవకలనీయము కాదు x = 0 వద్ద
సందర్భం ii) : x = 1

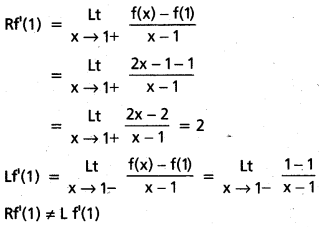
f(x), x = 1 వద్ద అవకలనీయము కాదు.
∴ f(x), 0, 1 వద్ద తప్ప x వాస్తవ విలువలన్నింటి వద్ద అవకలనీయము

ప్రశ్న 4.
క్రింది ప్రమేయం 1, 3 ల వద్ద అవకలనీయమేమో చూపండి.

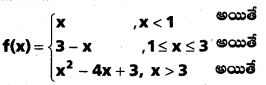
సాధన:
సందర్భం i) : x = 1

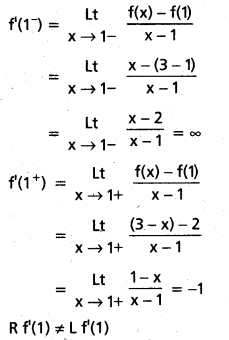
f(x), x = 1 వద్ద x = 1 అవకలనీయం కాదు
సందర్భం ii) : x = 3

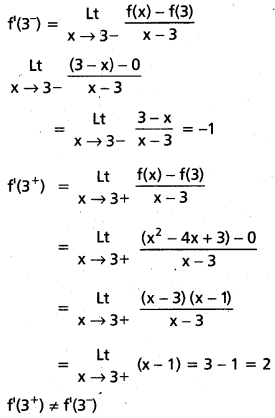
f(x) వద్ద x = 3 అవకలనీయం కాదు

ప్రశ్న 5.
క్రింది ప్రమేయం 2 వద్ద అవకలనీయమా ? సరి చూడండి.

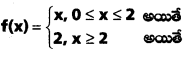
సాధన:


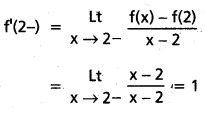
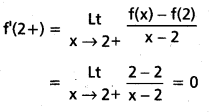
f'(2-) ≠ f'(2⁺) ; f(x) ప్రమేయం x = 2 వద్ద ఆవకలనీయం కాదు.