AP Inter 2nd Year Maths 2A Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Ex 10(a)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(a)

అభ్యాసం – 10(ఎ)

I.

ప్రశ్న 1.
ఒక విచ్ఛిన్న యాదృచ్ఛిక చలరాశి సంభావ్యతా విభాజన ప్రమేయం, x = 0, 1, 2 బిందువుల వద్ద మినహా తక్కిన అన్ని చోట్ల సున్న అవుతుంది. ఈ బిందువుల వద్ద, దాని విలువ P(0) = 3c³, P(1) = 4c – 10c², P(2) = 5c – 1, c > 0. c విలువ కనుక్కోండి.
సాధన:
P(X = 0) + P(X = 1) + P(X = 2) = 1
⇒ 3c³ + 4c – 10c² + 5c – 1 = 1
⇒ 3c³ – 10c² + 9c – 2 = 0
⇒ (c – 1) (c – 2) (3c – 1) = 0
⇒ c = 1 లేదా 2 లేదా \(\frac{1}{3}\)
c = 1, 2 అయిన P(0) > 1
∴ c = \(\frac{1}{3}\)

ప్రశ్న 2.
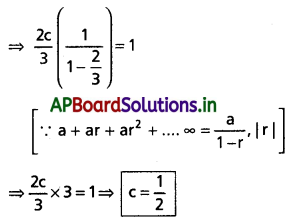
F(x) = \(c\left(\frac{2}{3}\right)^x\), x = 1, 2, 3 …….. ఒక విచ్ఛిన్న యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజన ప్రమేయాన్ని తృప్తిపరచేటట్లుగా, స్థిరరాశి c విలువను కనుక్కోండి.
సాధన:
దత్తాంశం నుండి

ప్రశ్న 3.

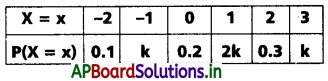
అనేది ఒక యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజనం k విలువ, X విస్తృతులను కనుక్కోండి. [Mar.’06]
సాధన:
సంభావ్యతల మొత్తం = 1
⇒ 0.1 + k + 0.2 + 2k + 0.3 + k = 1
⇒ 4k + 0.6 = 1
⇒ 4k = 1 – 0.6 = 0.4
⇒ k = \(\frac{0.4}{4}\) = 0.1
అంకమాధ్యమం (μ) = (-2) (0.1) + (-1) (k) + 0(0.2) + 1(2k) + 2(0.3) + 3k
= -0.2k + 0 + 2k + 0.6 + 3k
= 4k + 0.4
=4(0.1) + 0.4
= 0.4 + 0.4
= 0.8
μ = 0.8
విస్తృతి (σ²) = \(\sum_{i=1}^n x_i^2 P\left(x=x_i\right)\) – μ²
∴ విస్తృతి = 4(0.1) + 1(k) + 0(0.2) + 1(2k) + 4(0.3) + 9k – μ²
= 0.4 + k + 0 + 2k + 4(0.3) + 9k – μ²
= 12k + 0.4 + 1.2 – (0.8)²
= 12(0.1) + 1.6 – 0.64
= 1.2 + 1.6 – 0.64
∴ σ² = 2.8 – 0.64 = 2.16

ప్రశ్న 4.

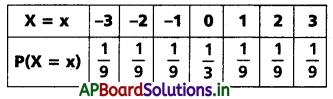
అనేది ఒక యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజనం. అయితే X విస్తృతిని కనుక్కోండి.
సాధన:

ప్రశ్న 5.
ఒక యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజనం ఈ క్రింది విధంగా ఉంది. [A.P. & T.S. Mar. ’16]

(i) k విలువ (ii) X అంకమధ్యమం (iii) P(0 < x < 5) లను కనుక్కోండి.
సాధన:
సంభావ్యతల మొత్తం = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k² + 10k – k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (10k – 1) (k + 1) = 0
⇒ k = \(\frac{1}{10}\), -1
∵ k > 0
∴ k = \(\frac{1}{10}\)
(i) k = \(\frac{1}{10}\)
(ii) X అంక మధ్యమం (μ) = \(\sum_{i=1}^n x_i P\left(x=x_i\right)\)
∴ μ = 0(0) + 1(k) + 2(2k) + 3(2k) + 4(3k) + 5(k²) + 6(2k²) + 7(7k² + k)
= 0 + k + 4k + 6k + 12k + 5k² + 12k² + 49k² + 7k
= 66k² + 30k
= \(66\left(\frac{1}{100}\right)+30 \times\left(\frac{1}{10}\right)\)
= 0.66 + 3
= 3.66
(iii) P(0 < x < 5)
P(0 < x < 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k
= 8 × \(\frac{1}{10}\)
= \(\frac{4}{5}\)

II.

ప్రశ్న 1.
ఒక యాదృచ్ఛిక చలరాశి వ్యాప్తి X = {0, 1, 2}. P(X = 0) = 3c³, P(X = 1) = 4c – 10c², P(X = 2) = 5c – 1 అయినప్పుడు (i) c విలువ (ii) P(X < 1), P(1 < X ≤ 2), P(0 < X ≤ 3) లను కనుక్కోండి. [Mar. ’13, ’11, ’07, ’05; May ’11]
సాధన:
P(X = 0) + P(X = 1) + P(X = 2) = 1
⇒ 3c³ + 4c – 10c² + 5c – 1 = 1
⇒ 3c³ – 10c² + 9c – 2 = 0
⇒ (c – 1) (c – 2) (3c – 1) = 0
⇒ c = 1 లేదా 2 లేదా \(\frac{1}{3}\)
c = 1, 2 అయిన P(X = 0) > 1
∴ c = \(\frac{1}{3}\)
(i) P(X < 1) = P(X = 0)
= 3 . c³
= 3 . \(\left(\frac{1}{3}\right)^3\)
= \(\frac{1}{9}\)
(ii) P(1 < X ≤ 2) = P(X = 2)
= 5c – 1
= \(\frac{5}{3}\) – 1
= \(\frac{2}{3}\)
(iii) P(0 < x ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3)
= 4c – 10c² + 5c – 1 + 0
= 9c – 10c² – 1
= \(\text { 9. } \frac{1}{3}-10 \cdot \frac{1}{9}-1\)
= \(\frac{8}{9}\)

ప్రశ్న 2.
ఒక యాదృచ్ఛిక చలరాశి X వ్యాప్తి (1, 2, 3, ………} P(X = K) = \(\frac{c^{\mathbf{k}}}{k !}\); (k = 1, 2, 3,…) అయితే c విలువను, P(0 < X < 3) ని కనుక్కోండి.
సాధన:
సంభావ్యతల మొత్తం = 1