Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(b) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(b)
అభ్యాసం – 10(బి)
I.
ప్రశ్న 1.
ఒక నాణేన్ని n సార్లు ఎగరవేసే ప్రయోగంలో, బొమ్మలు పడే సంఖ్యను, చలరాశి X సూచిస్తుంది. P(X = 4), P(X = 5), P(X = 6) లు అంకశ్రేఢి లో ఉన్నాయి. అప్పుడు n కనుక్కోండి.
సాధన:
X ద్విపద విభాజనాన్ని పాటిస్తుంది.
p = \(\frac{1}{2}\), q = \(\frac{1}{2}\) (∵ నాణేన్ని ఎగరవేస్తే)
Hint: a, b, c లు A.P. లో ఉంటే 2b = a + c (లేదా) b – a = c – a
P(X = 4), P(X = 5), P(X = 6) లు A.P. లో ఉన్నాయి.

⇒ 2 × 30(n – 4) = 5[30 + n2 – 9n + 20]
⇒ 12n – 48 = n2 – 9n – 50
⇒ n2 – 21n + 98 = 0
⇒ n2 – 14n – 7n + 98 = 0
⇒ n(n – 14) – 7(n – 14) = 0
⇒ (n – 7) (n – 14) = 0
∴ n = 7 లేదా 14
![]()
ప్రశ్న 2.
కనీసం ఒక బొమ్మ పడుతూ, సంభావ్యత కనీసం 0.8 కావడానికి, ఒక నిష్పాక్షిక నాణేన్ని ఎగరవేయాల్సిన గరిష్ఠ సంఖ్యను కనుక్కోండి.
సాధన:
ఒక నిష్పాక్షిక నాణేన్ని n సార్లు ఎగరవేసితిమి అనుకోండి.
బొమ్మల సంఖ్యను చలరాశి X సూచిస్తుంది.
X ద్విపద విభాజనాన్ని పాటిస్తుంది. n, p లు పరామితులు.
ఇచ్చట p = \(\frac{1}{2}\)
దత్తాంశం నుండి P(X ≥ 1) ≥ 0.8
⇒ 1 – P(X = 0) ≥ 0.8
⇒ P(X = 0) ≤ 0.2
⇒ \({ }^n C_o\left(\frac{1}{2}\right)^n\) ≤ 0.2
⇒ \(\left(\frac{1}{2}\right)^n \leq \frac{1}{5}\)
n ≥ ౩ అయిన పై అసమీకరణం సత్యం కనుక n గరిష్ఠ విలువ 3.
ప్రశ్న 3.
ఒక బాంబు, ఒక వంతెనను కూల్చివేసే సంభావ్యత \(\frac{1}{2}\), వంతెనను కూల్చడానికి 3 సార్లు (వరుసగా కానవసరం లేదు) నేరుగా కొట్టవలసి వస్తుంది. వంతెన కూలే సంభావ్యత 0.9 కంటే ఎక్కువ కావడానికి కావలసిన బాంబుల కనిష్ట సంఖ్యను కనుక్కోండి.
సాధన:
వంతెనను కూల్చడానికి కావలసిన బాంబుల కనిష్ట సంఖ్య n, యాదృచ్ఛిక చలరాశి X బాంబుల సంఖ్యను తెలిపితే,
p = \(\frac{1}{2}\)
ఇప్పుడు P(X ≥ 3) > 0.9
⇒ 1 – P(X < 3) > 0.9
⇒ P(X < 3) < 0.1
⇒ P(X = 0) + P(X = 1) + P (X = 2) < 0.1


⇒ 5(n2 + n + 2) < 2n
యత్నదోష పద్ధతిన n ≥ 9 పై అసమీకరణాన్ని తృప్తి పరుస్తుంది.
∴ కనిష్ట విలువ 9.
ప్రశ్న 4.
ఒక ద్విపద చలరాశి మధ్యమం, విస్తృతుల మధ్య భేదం \(\frac{5}{9}\) అయితే, ప్రయోగాన్ని 5 సార్లు నిర్వహించినప్పుడు 2 సార్లు సఫలం అయ్యే ఘటన సంభావ్యతను కనుక్కోండి.
సాధన:
n = 5, p లు ద్విపద విభాజనానికి పరామితులు
మధ్యమం – విస్తృతి = \(\frac{5}{9}\)

∴ 2 సార్లు సఫలం అయ్యే ఘటన సంభావ్యత = \(\frac{80}{243}\)
![]()
ప్రశ్న 5.
ప్రయాణానికి సంసిద్ధమైన 9 ఓడలలో ఒకటి మునిగిపోయే ప్రమాదం ఉంది. 6 ఓడలు ప్రయాణానికి సంసిద్ధమైతే (i) కనీసం ఒకటి క్షేమంగా చేరడానికి (ii) సరిగ్గా 3 క్షేమంగా చేరడానికి గల సంభావ్యతలను కనుగొనండి. [Mar. ’08]
సాధన:
p = ఓడ మునిగిపోవటానికి సంభావ్యత = \(\frac{1}{9}\)
q = 1 – p
= 1 – \(\frac{1}{9}\)
= \(\frac{8}{9}\)
ఓడల సంఖ్య = n = 6

ప్రశ్న 6.
ఒక ద్విపద చలరాశి X అంకమధ్యం, విస్తృతులు వరుసగా 2.4, 1.44 అయితే, P(1 < X ≤ 4) ను కనుక్కోండి. [May ’06]
సాధన:
X అంకమధ్యమం = np = 2.4 ……(1)
విస్తృతి = npq = 1.44 ………(2)
(2) ను (1) చే భాగించగా
\(\frac{n p q}{n p}=\frac{1.44}{2.4}\)
q = 0.6 = \(\frac{3}{5}\)
p = 1 – q
= 1 – 0.6
= 0.4
= \(\frac{2}{5}\)
(1) లో వ్రాయగా
n(0.4) = 2.4
n = \(\frac{2.4}{0.4}\) = 6
P(1 < X ≤ 4) = P(X = 2) + P(X = 3) + P(X = 4)
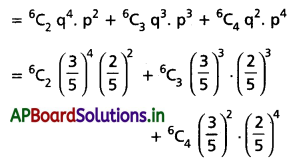

ప్రశ్న 7.
ఒక కంపెనీ తయారు చేసే విద్యుత్ (ఎలక్ట్రిక్) బల్బులలో 10 శాతం లోపం ఉన్నవని ఇచ్చారు. 20 బల్బులలో 2 కంటే ఎక్కువ బల్బులు లోపం ఉన్నవి కాగల సంభావ్యతను కనుక్కోండి.
సాధన:
p = బల్బు లోపం కలది కావటానికి సంభావ్యత = \(\frac{1}{10}\)
q = 1 – p
= 1 – \(\frac{1}{10}\)
= \(\frac{9}{10}\)
n = బల్బుల సంఖ్య = 20
P(X > 2) = 1 – P(X ≤ 2)
= 1 – [P(X = 0) + P(X = 1) + P(X = 2)]

![]()
ప్రశ్న 8.
సగటున ప్రతి 30 రోజులలో 12 రోజులు వర్షం కురిస్తే, ఒక వారంలో 3 రోజులు వర్షం కురిసే సంభావ్యతను కనుక్కోండి.
సాధన:
p = \(\frac{12}{30}=\frac{2}{5}\) (దత్తాంశము నుండి)
q = 1 – p
= 1 – \(\frac{2}{5}\)
= \(\frac{3}{5}\)
n = 7, r = 3
వారంలో 3 రోజులు వర్షం కురిసే సంభావ్యత P(X = 3)

ప్రశ్న 9.
అంకమధ్యమం 6, విస్తృతి 2 గల ఒక ద్విపద విభాజనం లోని మొదటి రెండు పదాలను కనుక్కోండి.
సాధన:
n, p లు ద్విపద విభాజన పరిమితులు.
మధ్యమం (np) = 6 …..(1)
విస్తృతి (npq) = 2 …..(2)
అప్పుడు \(\frac{\mathrm{npq}}{\mathrm{np}}=\frac{2}{6}\)
q = \(\frac{1}{3}\)
p = 1 – q
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
(1) నుండి nP = 6
n(\(\frac{2}{3}\)) = 6
n = \(\frac{18}{2}\) = 9
విభాజనంలో మొదటి పదం P(X = 0) = \({ }^9 C_0\left(\frac{1}{3}\right)^9=\frac{1}{3^9}\)
రెండవ పదం P(X = 1) = \({ }^9 C_1\left(\frac{1}{3}\right)^8\left(\frac{2}{3}\right)=\frac{2}{3^7}\)
ప్రశ్న 10.
ఒక నగరంలో 50 రోజుల వ్యవధిలో 10 ప్రమాదాలు సంభవిస్తాయి. ప్రమాదాల సంఖ్య ఒక పాయిజాన్ విభాజనాన్ని అనుసరిస్తుందనుకుంటే, ఒక్క రోజులో 3 లేదా అంతకంటే ఎక్కువ ప్రమాదాలు జరగగల సంభావ్యతను కనుక్కోండి.
సాధన:
రోజులో సగటు ప్రమాదాల సంఖ్య
λ = \(\frac{10}{50}=\frac{1}{5}\) = 0.2
రోజులో 3 లేదా అంతకంటే ఎక్కువ ప్రమాదాలు జరగగల సంభావ్యత
P(X ≥ 3) = \(\sum_{k=3}^{\infty} \mathrm{e}^{-\lambda} \cdot \frac{\lambda^k}{k !}\), λ = 0.2
II.
ప్రశ్న 1.
5 నాణేలను 320 సార్లు ఎగరవేశారు. బొమ్మల సంఖ్యకు పౌనఃపున్య విభాజనాన్ని కనుక్కుని, ఫలితాన్ని పట్టికగా రాయండి.
సాధన:
5 నాణేలను 320 సార్లు ఎగరవేశారు.
బొమ్మ రావడానికి సంభావ్యత
p = \(\frac{1}{2}\)
n = 5
q = 1 – p
= 1 – \(\frac{1}{2}\)
= \(\frac{1}{2}\)
X బొమ్మలు రావటానికి సంభావ్యత

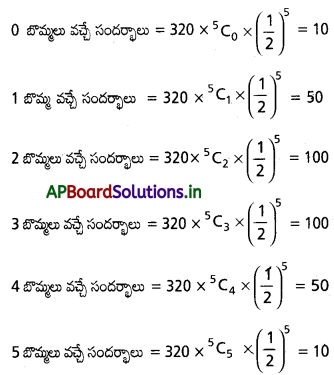

ప్రశ్న 2.
ఒక ప్రశ్నాపత్రంలోని 10 సమాధానాలకు కనీసం సరైనవిగా ఊహించగల సంభావ్యత కింది సందర్భాలలో కనుక్కోండి. [Mar. ’14]
(i) ప్రశ్నాపత్రంలో తప్పు, ఒప్పులు గల ప్రశ్నలు ఉన్నప్పుడు
(ii) ప్రశ్నాపత్రంలో 4 ఐచ్ఛిక సమాధానాలుండే బహుళైచ్ఛిక ప్రశ్నలున్నప్పుడు
సాధన:
(i) ఒప్పు లేదా తప్పులు సమాధానాలు కనుక
సఫల సంభావ్యత p = \(\frac{1}{2}\)
విఫల సంభావ్యత q = \(\frac{1}{2}\)
10 సమాధానాలలో 6 సరియైనట్టివిగా ఊహించగల సంభావ్యత
P(X = 6) = \({ }^{10} C_6\left(\frac{1}{2}\right)^{10-6}\left(\frac{1}{2}\right)^6\)
= \({ }^{10} C_6\left(\frac{1}{2}\right)^{10}\)
(ii) 4 సాధ్యమయ్యే సమాధానాలు ఉన్న ప్రశ్నలు
కనుక సఫల సంభావ్యత p = \(\frac{1}{4}\)
విఫల సంభావ్యత q = \(\frac{3}{4}\)
10 సమాధానాలలో 6 సరియైనట్టివిగా ఊహించగల సంభావ్యత
P(X = 6) = \({ }^{10} C_6\left(\frac{3}{4}\right)^{10-6}\left(\frac{1}{4}\right)^6\)
= \({ }^{10} C_6 \cdot \frac{3^4}{4^{10}}\)
![]()
ప్రశ్న 3.
ఒక నిముషంలో ఒక సినిమా టికెట్ కౌంటర్ వద్దకు వచ్చి చేరే వ్యక్తుల సంఖ్య, 6 పరామితితో ఒక పాయిజాన్ విభాజనంగా ఉంటుంది.
(i) ఒక నిర్దిష్ట నిమిషంలో ఏ ఒక్కరూ క్యూలో చేరని
(ii) ఒక నిమిషంలో ఇద్దరు లేదా అంతకంటే ఎక్కువ మంది క్యూలో వచ్చి చేరే సంభావ్యతలను కనుక్కోండి.
సాధన:
λ = 6
(i) ఒక నిర్దిష్ట నిమిషంలో ఏ ఒక్కరూ క్యూలో చేరని సంభావ్యత
P(X = 0) = \(\frac{\mathrm{e}^{-\lambda} \lambda^0}{0 !}\) = e-6
(ii) ఒక నిముషంలో ఇద్దరూ లేదా అంతకంటే ఎక్కువ మంది క్యూలో వచ్చి చేరే సంభావ్యత
P(X ≥ 2) = 1 – P(X ≤ 1)
= 1 – [P(X = 0) + P(X = 1)]
= 1 – \(\left[\mathrm{e}^{-\lambda} \frac{\lambda^0}{0 !}+\frac{e^{-\lambda} \cdot \lambda^1}{1 !}\right]\)
= 1 – \(\left[\mathrm{e}^{-6}+\frac{\mathrm{e}^{-6} \cdot(6)}{1 !}\right]\)
= 1 – 7e-6