Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 3 వర్గసమాసాలు Exercise 3(c) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 3 వర్గసమాసాలు Exercise 3(c)
అభ్యాసం – 3(సి)
I.
ప్రశ్న 1.
క్రింది అసమీకరణాలను బీజీయ పద్ధతిలో సాధించండి.
(i) 15x2 + 4x – 4 ≤ 0
సాధన:
15x2 + 4x – 4 ≤ 0
15x2 – 6x + 10x – 4 ≤ 0
3x(5x – 2) + 2(5x – 2) ≤ 0
(3x + 2) (5x – 2) ≤ 0
x2 గుణకం = 15 > 0,
దత్త సమాసం విలువ x ≤ 0 కనుక
\(\frac{-2}{3}, \frac{2}{5}\) ల మధ్య ఉంటుంది.
i.e., \(\frac{-2}{3} \leq x \leq \frac{2}{5}\)
(ii) x2 – 2x + 1 < 0
సాధన:
(x – 1)2 < 0
x యొక్క ఏ వాస్తవ విలువపై అసమీకరణాన్ని ధృవీకరించదు.
కనుక సాధన సమితి = φ లేదా దత్త అసమీకరణానికి సాధన లేదు.
![]()
(iii) 2 – 3x – 2x2 ≥ 0
సాధన:
-(2x2 + 3x – 2) ≥ 0
⇒ -(2x2 + 4x – x – 2) ≥ 0
⇒ [2x(x + 2) – 1(x + 2)] ≥ 0
⇒ -(2x – 1) (x + 2) ≥ 0
x2 గుణకం = -2 < 0, సమాసం ≥ 0
⇒ x విలువ -2, \(\frac{1}{2}\) ల మధ్య ఉంటుంది.
i.e., -2 ≤ x ≤ \(\frac{1}{2}\)
(iv) x2 – 4x – 21 ≥ 0
సాధన:
x2 – 4x – 21 ≥ 0
x2 – 7x + 3x – 21 ≥ 0
x(x – 7) + 3(x – 7) ≥ 0
(x + 3)(x – 7) ≥ 0
x2 గుణకం = 1 > 0, సమాసం ≥ 0
x విలువ -3, 7 ల మధ్య ఉండదు.
i.e., x ∈ (-∞, -3] ∪ [7, ∞)
II.
ప్రశ్న 1.
క్రింది అసమీకరణాలను రేఖాచిత్ర పద్ధతిలో సాధించండి.
(i) x2 – 7x + 6 > 0
సాధన:
f(x) = x2 – 7x + 6
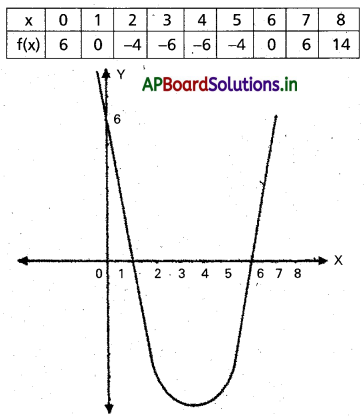
f(x) > 0 ⇒ y > 0
కనుక సాధన x < 1 మరియు x > 6.
(ii) 4 – x2 > 0
సాధన:
f(x) = 4 – x2 అనుకొనుము.
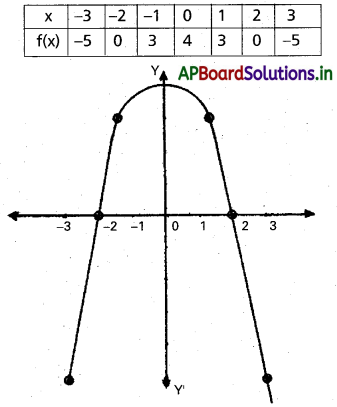
f(x) > 0 ⇒ y > 0
సాధన సమితి = {x/-2 < x < 2}
(iii) 15x2 + 4x – 4 ≤ 0
సాధన:
f(x) = 15x22 + 4x – 4 అనుకోండి.
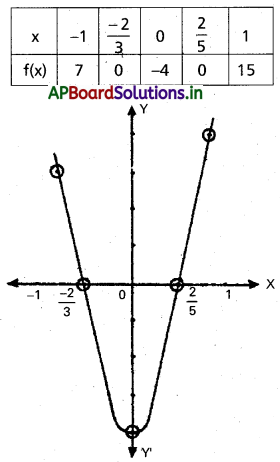
f(x) ≤ 0 ⇒ y ≤ 0
సాధన సమితి = \(\left\{x / \frac{-2}{3} \leq x \leq \frac{2}{5}\right\}\)
![]()
(iv) x2 – 4x – 21 ≥ 0
సాధన:
f(x) = x2 – 4x – 21 అనుకోండి.
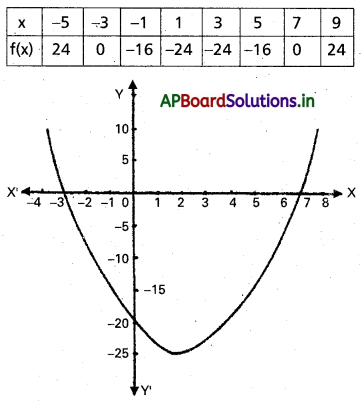
f(x) ≥ 0 ⇒ y ≥ 0
సాధన సమితి = {x/x ∈ (-∞, -3] ∪ [7, ∞)}
ప్రశ్న 2.
క్రింది అసమీకరణాలను సాధించండి.
(i) \(\sqrt{3 x-8}\) < -2
సాధన:
దత్త అసమీకరణానికి L.H.S. ధనాత్మకము, R.H.S. ఋణాత్మకము.
కనుక సాధన సమితి = φ లేదా సాధన సమితి వ్యవస్థితం కాదు.
(ii) \(\sqrt{-x^2+6 x-5}\) > 8 – 2x
సాధన:
\(\sqrt{-x^2+6 x-5}\) > 8 – 2x
⇔ -x2 + 6x – 5 ≥ 0
మరియు (i) 8 – 2x < 0 లేదా (ii) 8 – 2x ≥ 0
-x2 + 6x – 5 = -(x2 – 6x + 5) = -(x – 1) (x – 5)
కాబట్టి -x2 + 6x – 5 ≥ 0 ⇔ x ∈ [1, 5]
(i) -x2 + 6x – 5 ≥ 0 మరియు 8 – 2x < 0
⇔ x ∈ [1, 5] మరియు x > 4
⇔ x ∈ [4, 5] ……..(1)
(ii) -x2 + 6x – 5 ≥ 0 మరియు 8 – 2x ≥ 0
∵ \(\sqrt{\left(-x^2+6 x-5\right)}\) > 8 – 2x
⇔ -x2 + 6x – 5 > (8 – 2x)2, మరియు 8 – 2x ≥ 0
⇔ -x2 + 6x – 5 > 64 + 4×2 – 32x, x ≤ 4
⇔ 5x2 – 38x + 69 < 0, x ≤ 4
⇔ 5x2 – 15x – 23x + 69 < 0, x ≤ 4
⇔ (5x – 23) (x – 3) < 0, x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)), x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)) ∧ (-∞, 4)
⇔ x ∈ (3, 4) …….(2)
కాబట్టి (1), (2) ల నుండి, దత్త సమీకరణానికి సాధన సమితి
x ∈ (4, 5) ∪ (3, 4)
⇒ x = (3, 5) లేదా 3 < x ≤ 5