AP Inter 2nd Year Maths 2B Solutions Chapter 6 సమాకలనం Ex 6(e)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 6 సమాకలనం Exercise 6(e) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 6 సమాకలనం Exercise 6(e)

అభ్యాసం 6(ఇ)

I. కింది సమాకలనులను గణించండి.

ప్రశ్న 1.
∫\(\frac{x-1}{(x-2)(x-3)}\) dx
సాధన:

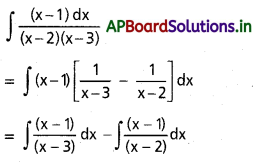
= ∫\(\left(1+\frac{2}{x-3}\right)\) dx – ∫\(\left(1+\frac{1}{x-2}\right)\) dx
= x + 2ln |x – 3| – x – ln |x – 2| + C
= 2log |x – 3| – log |x – 2| + C

ప్రశ్న 2.
∫\(\frac{x^2}{(x+1)(x+2)^2}\) dx
సాధన:
\(\frac{x^2}{(x+1)(x+2)^2}\) ≡ \(\frac{A}{x+1}\) + \(\frac{B}{x+2}\) + \(\frac{C}{(x+2)^2}\)
⇒ x² = A(x + 2)² + B(x + 1)(x + 2) + C (x + 1)
x = -2 లో (1)
(-2)² = A(0) + B(0) + C(-2 + 1) ⇒ C = -4
x = -1 లో (1)
(-1)² = A(-1 + 2)² + 8(0) + C(0)
⇒ A = 1
(1) లో x² గుణకాలను సమానం చేయండి.
1 = A + B
⇒ B = 1 – A = 1 – 1 = 0

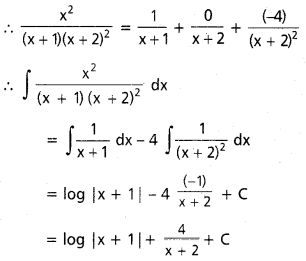
ప్రశ్న 3.
∫\(\frac{x+3}{(x-1)\left(x^2+1\right)}\) (May 07)
సాధన:
\(\frac{x+3}{(x-1)\left(x^2+1\right)}\) = \(\frac{A}{x-1}\) + \(\frac{\mathrm{Bx}+\mathrm{C}}{\mathrm{x}^2+1}\) అనుకొనుము
⇒ (x + 3) = A(x² + 1) + (Bx + C) (x – 1) – (1)
(1 ) లో x = 0 ప్రతిక్షేపించగా
3 = A(1) + C(-1)
⇒ A – C = 3 ⇒ C = A – 3 = 2 – 3 = 1
(1) లో x² గుణకాలను సమానం చేయండి.
0 = A + B
⇒ B = -A = -2

ప్రశ్న 4.
∫\(\frac{d x}{\left(x^2+a^2\right)\left(x^2+b^2\right)}\)
సాధన:

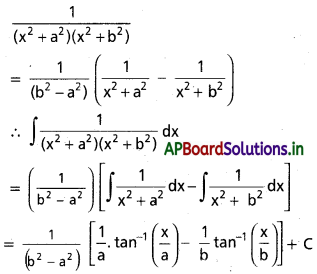
ప్రశ్న 5.
∫\(\frac{d x}{e^x+e^{2 x}}\)
సాధన:

ప్రశ్న 6.
∫\(\frac{d x}{(x+1)(x+2)}\)
సాధన:

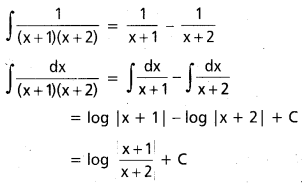
ప్రశ్న 7.
∫\(\frac{1}{e^x-1}\) dx
సాధన:

ప్రశ్న 8.
∫\(\frac{1}{(1-x)\left(4+x^2\right)}\) dx
సాధన:
∫\(\frac{1}{(1-x)\left(4+x^2\right)}\) = \(\frac{A}{1-x}\) + \(\frac{B x+C}{4+x^2}\) అనుకోండి
⇒ 1 = A(4 + x²) + (Bx + C)(1 – x) —- (1)
(1) లో x = 1 ప్రతిక్షేపించగా
1 = A(4 + 1) ⇒ A = \(\frac{1}{5}\)
(1) లో x = 0 ప్రతిక్షేపించగా
1 = A(4) + C(1)
⇒ C = 1 – 4A = 1 – 4\(\left(\frac{1}{5}\right)\) = \(\frac{5-4}{5}\) = \(\frac{1}{5}\)
(1) లో x² గుణకాలను సమానం చేయగా
0 = A – B
⇒ B = A = \(\frac{1}{5}\)

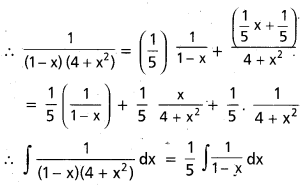
ప్రశ్న 9.
∫\(\frac{2 x+3}{x^3+x^2-2 x}\) dx
సాధన:

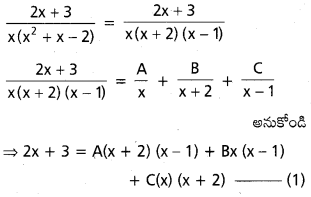
⇒ (1) లో x = 0 ప్రతిక్షేపించగా
3 = A(2)(-1) + B(0) + C(0)
⇒ A = –\(\frac{3}{2}\)
(1) లో x = 1 ప్రతిక్షేపించగా
2 + 3 = A(0) + B(0) + C(1)(3)
⇒ C = \(\frac{5}{3}\)
(1) లో x = -2 ప్రతిక్షేపించగా
2(-2) + 3 = A(0) + B(-2)(-2 – 1) + C(0)
⇒ -1 = 6B ⇒ B = \(\frac{-1}{6}\)

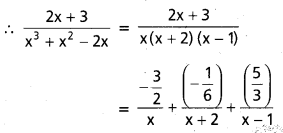
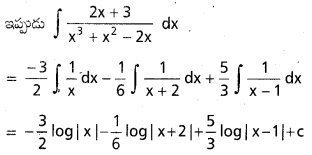
II. కింది సమాకలనులను గణించండి.

ప్రశ్న 1.
∫\(\frac{d x}{6 x^2-5 x+1}\)
సాధన:

ప్రశ్న 2.
∫\(\frac{d x}{x(x+1)(x+2)}\)
సాధన:
\(\frac{1}{x(x+1)(x+2)}\) ≡ \(\frac{A}{x}\) + \(\frac{\mathrm{B}}{\mathrm{x}+1}\) + \(\frac{c}{x+2}\)
⇒ 1 ≡ A(x + 1)(x + 2) + B(x)(x + 2) + C(x)(x + 1)
x = 0 ప్రతిక్షేపించగా
1 = A(1) (2) + B(0) + C(0) ⇒ A = \(\frac{1}{2}\)
x = -1 ప్రతిక్షేపించగా
1 = A(0) + B(-1)(-1 + 2) + C(0)
⇒ 1 = -B ⇒ B = -1
x = -2 ప్రతిక్షేపించగా

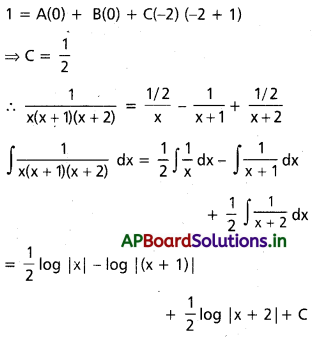
ప్రశ్న 3.
∫\(\frac{3 x-2}{(x-1)(x+2)(x-3)}\) dx
సాధన:
\(\frac{3 x-2}{(x-1)(x+2)(x-3)}\) ≡ \(\frac{A}{x-1}\) + \(\frac{B}{x+2}\) + \(\frac{c}{x-3}\)
⇒ 3x – 2 = A(x + 2) (x – 3) + B(x – 1)(x – 3) + C(x – 1)(x + 2)
x = 1 ప్రతిక్షేపించగా
3(1) – 2 = A(1 + 2)(1 – 3) + B(0) + C(0)
⇒ A = \(\frac{-1}{6}\)
x = 3 ప్రతిక్షేపించగా
3(3) – 2 = A(0) + B(0) + C (3 – 1) (3 + 2)
C = \(\frac{7}{10}\)
x = -2 ప్రతిక్షేపించగా
3(-2) – 2 = A(0) + B(-2-1)(-2-3) + C(0) – 8
= 15B ⇒ B = \(\frac{-8}{15}\)

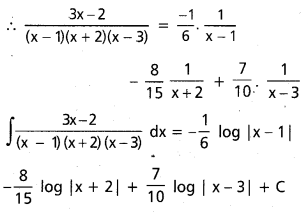
ప్రశ్న 4.
∫\(\frac{7 x-4}{(x-1)^2(x+2)}\) dx
సాధన:
\(\frac{7 x-4}{(x-1)^2(x+2)}\) ≡ \(\frac{A}{x-1}\) + \(\frac{B}{(x-1)^2}\) + \(\frac{c}{x+2}\)
⇒ 7x – 4 = A(x – 1) (x + 2) + B(x + 2) + C(x – 1)² —- (1)
x = 1 లో ప్రతిక్షేపించగా
7 – 4 = A(0) + B(1 + 2) ⇒ B = 1
x = -2 లో (1) ప్రతిక్షేపించగా
7(-2) – 4 = A(0) + B(0) + C(-2-1)²
⇒ -18 = 9C ⇒ C = -2

III. కింది సమాకలనులను గణించండి.

ప్రశ్న 1.
∫\(\frac{1}{(x-a)(x-b)(x-c)}\) dx
సాధన:

x = b ప్రతిక్షేపించగా
1 = A(0) + B(b – a) (b – c) + C(0)

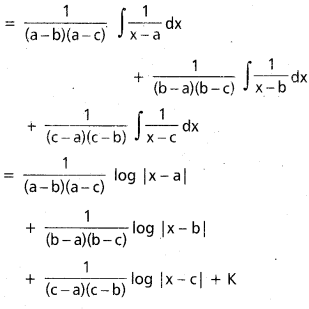
ప్రశ్న 2.
∫\(\frac{2 x+3}{(x+3)\left(x^2+4\right)}\) dx
సాధన:
\(\frac{2 x+3}{(x+3)\left(x^2+4\right)}\) = \(\frac{A}{x+3}\) + \(\frac{B x+C}{x^2+4}\) అనుకోండి
2x + 3 = A(x² + 4) + (Bx + C) (x + 3)
x = -3 ⇒ -3 = A(9 + 4) = 13 A
A = –\(\frac{3}{13}\)
x² గుణకాలు సమానం చేయగా
0 = A + B ⇒ B = -A = \(\frac{3}{13}\)
స్థిరపదాలు సమానం చేయగా
3 = 4A + 3C
3C = 3 – 4A = 3 + \(\frac{12}{13}\) = \(\frac{39+12}{13}\) = \(\frac{51}{13}\)

ప్రశ్న 3.
∫\(\frac{2 x^2+x+1}{(x+3)(x-2)^2}\) dx
సాధన:
\(\frac{2 x^2+x+1}{(x+3)(x-2)^2}\) = \(\frac{A}{x+3}\) + \(\frac{B}{x-2}\) + \(\frac{C}{(x-2)^2}\) అనుకోండి
2x² + x + 1 = A(x – 2)² + B(x + 3) (x – 2) + C(x + 3)
x = 2 ⇒ 8 + 2 + 1 = C(2 + 3) = 5C
⇒ C = \(\frac{11}{5}\)
x = -3 ⇒ 18 – 3 + 1
= A(-5)² = 25A ⇒ A = \(\frac{16}{25}\)
x² గుణకాలు సమానం చేయగా

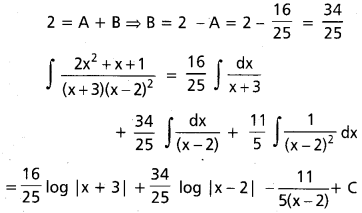
ప్రశ్న 4.
∫\(\frac{d x}{x^3+1}\)
సాధన:

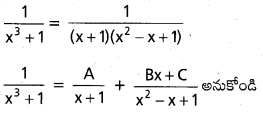
⇒ 1 = A(x² – x + 1) + (Bx + C)(x + 1) —– (1)
(1) లో x = -1 ప్రతిక్షేపించగా
1 = A(1 + 1 + 1) + (-B + C)(0)
⇒ 3A = 1 ⇒ A = \(\frac{1}{3}\)
(1) లో x = 0 ప్రతిక్షేపించగా
1 = A(1) + C(1)
⇒ C = 1 – A = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
x² గుణకాలు సమానం చేయగా
O = A + B ⇒ B = -A = –\(\frac{1}{3}\)

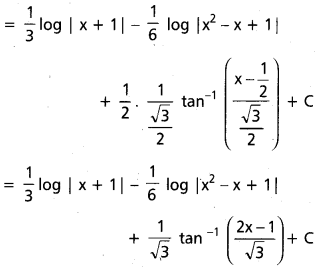
ప్రశ్న 5.
∫\(\frac{\sin x \cos x}{\cos ^2 x+3 \cos x+2}\) dx
సాధన:
cos x = t ⇒ – sin x dx = dt
∫\(\frac{\sin x \cdot \cos x d x}{\cos ^2 x+3 \cos x+2}\) = ∫\(\frac{-t d t}{t^2+3 t+2}\)

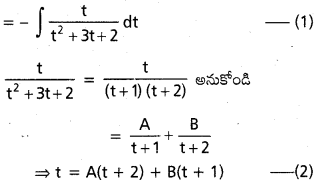
(2) లో t = -1 ప్రతిక్షేపించగా
-1 = A(-1 + 2) ⇒ A = -1
(2) లో t = -2 ప్రతిక్షేపించగా
-2 = B(-2 + 1) ⇒ B = 2