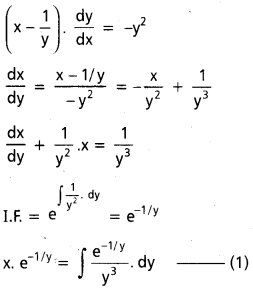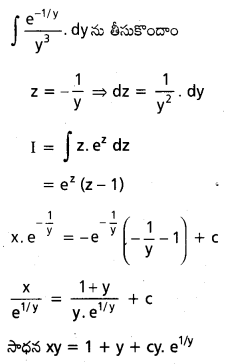AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Ex 8(e)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(e) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(e)

అభ్యాసం – 8(ఇ)

క్రింది అవకలన సమీకరణాలను ఏకఘాతీయ సమీకరణ రూపంలో రాసి I.F. లను కనుక్కోండి.

ప్రశ్న 1.
x \(\frac{d x}{d y}\) – y = 2x² sec² 2x
సాధన:
x \(\frac{d x}{d y}\) – y = 2x² sec² 2x
\(\frac{d x}{d y}\) – \(\frac{1}{x} \cdot y\) = 2x. sec² 2x
x లో రేఖీయ సమీకరణము
I.F. = \(\int_e-\frac{1}{x} \log x\) = e^{-log x} = e^{log 1/x} = \(\frac{1}{x}\)

ప్రశ్న 2.
y \(\frac{d x}{d y}\) – x = 2y³
సాధన:
y \(\frac{d x}{d y}\) – x = 2y³
\(\frac{d x}{d y}\) – \(\frac{1}{y} \cdot x\) = 2y²
I.F. = \(e^{\int-\frac{1}{y}} d y\) = e^{-log y} = \(e^{\log \frac{1}{y}}\) = \(\frac{1}{y}\)

II. క్రింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
\(\frac{d y}{d x}\) + y tan x = cos³ x (May ’11)
సాధన:
I.F. = \(e^{\int \tan x d x}\) = e^{log sec x} = sec x
y. sec x = \(\int \sec x \cdot \cos ^3 x d x\)
= \(\int \cos ^2 x d x\)
= \(\frac{1}{2} \int(1+\cos 2 x) d x\)
= \(\frac{1}{2}\left(x+\frac{\sin 2 x}{2}\right)\) + c
సాధన 2y = x cos x + sin x. cos² x + c. cos x

ప్రశ్న 2.
\(\frac{d y}{d x}\) + y sec x = tan x
సాధన:

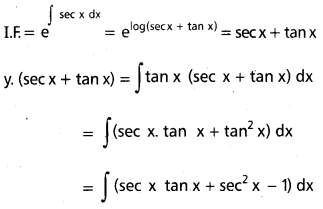
సాధన
y(sec x + tan x) = sec x + tan x – x + c

ప్రశ్న 3.
\(\frac{d y}{d x}\) – y tan x = e^x sec x.
సాధన:
I.F. = \(e^{-\int \tan x d x}\) = e^{log cos x} = cos x
y. cos x = ∫e^x. sec x. cos x dx = ∫ e^x dx
= e^x + c

ప్రశ్న 4.
x. \(\frac{d y}{d x}\) + 2y = log x.
సాధన:
I.F. = \(e^{\int \frac{2}{x} d x}\) = e^{2 log x} = e^{log x}2 = x²
= ∫x log x dx
= ∫log x. \(\left(\frac{x^2}{2}\right)\) – \(\frac{1}{2} \int x^2 \cdot \frac{1}{x} d x\)
= \(\frac{x^2}{2}\) log x – \(\frac{x^2}{4}\) + c

ప్రశ్న 5.
(1 + x²)\(\frac{\mathbf{d y}}{\mathbf{d x}}\) + y = \(e^{\tan ^{-1} x}\). (May ’07) (A.P. Mar. ’16)
సాధన:
\(\frac{d y}{d x}\) + \(\frac{1}{1+x^2}\).y = \(\frac{e^{\tan ^{-1} x}}{1+x^2}\)

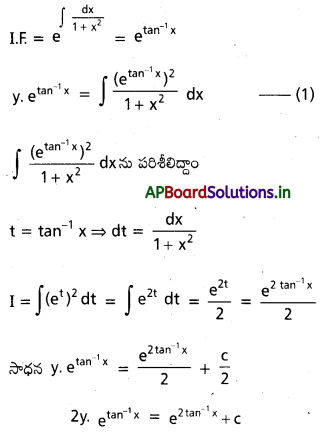
ప్రశ్న 6.
\(\frac{d y}{d x}\) + \(\frac{2 y}{x}\) = 2x²
సాధన:
I.F. = \(e^{\int \frac{2}{x} d x}\) = e^{2 log x} = \(e^{\log x^2}\) = x²
y. x² = ∫2x⁴ dx = \(\frac{2 x^5}{5}\) + c

ప్రశ్న 7.
\(\frac{d y}{d x}\) + \(\frac{4 x}{1+x^2} y\) = \(\frac{1}{\left(1+x^2\right)^2}\)
సాధన:

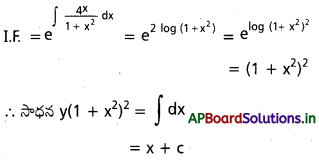
ప్రశ్న 8.
x\(\frac{d y}{d x}\) + y = (1 + x)e^x
సాధన:

ప్రశ్న 9.
\(\frac{d y}{d x}\) + \(\frac{3 x^2}{1+x^3}\)y = \(\frac{1+x^2}{1+x^3}\)
సాధన:

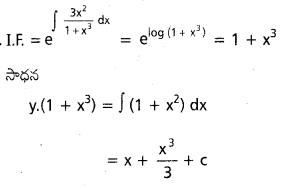
ప్రశ్న 10.
\(\frac{d y}{d x}\) – y = -2e^-x.
సాధన:
I.F = \(e^{\int-d x}\) = e^-x
y. e^-x = -2∫e^2xdx = e^-2x + c
y = e^-x + c. e^x

ప్రశ్న 11.
(1 + x²)\(\frac{d y}{d x}\) + y = tan^-1x.
సాధన:

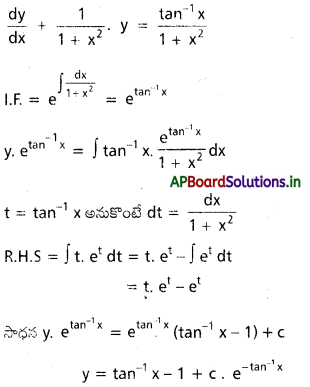
ప్రశ్న 12.
\(\frac{d y}{d x}\) + y tan x = sin x. [T.S. Mar. 16]
సాధన:
I.F. e^{∫tan x dx} = e^{log sec x} = sec x
y. sec x = ∫sin x. sec x dx = ∫tan x dx
= log sec x + c

III. ఈ క్రింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
cos x. \(\frac{d y}{d x}\) + y sin x = sec² x
సాధన:
\(\frac{d y}{d x}\) + tan x. y = sec³ x
I.F. = e^{∫tan x dx} = e^{log sec x} = sec x
y. sec x = ∫sec⁴x dx = ∫(1 + tan² x) sec² x dx
= tan x + \(\frac{\tan ^3 x}{3}\) + c

ప్రశ్న 2.
sec x. dy = (y + sin x) dx.
సాధన:

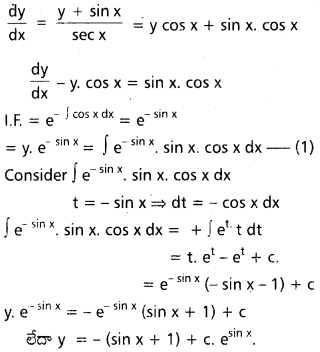
ప్రశ్న 3.
x log x. \(\frac{d y}{d x}\) + y = 2 log x
సాధన:

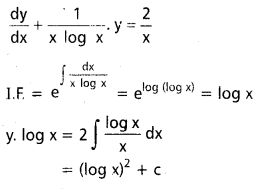
ప్రశ్న 4.
(x + y + 1)\(\frac{d y}{d x}\) = 1 (Mar. 05)
సాధన:
\(\frac{d x}{d y}\) = x + y + 1
\(\frac{d x}{d y}\) – x = y + 1
I.F. = e^∫-dy = e^-y
x. e^-y = ∫e^-y (y + 1) dy
= -(y + 1). e^-y + ∫e^-y. dy
= -(y + 1) e^-y – e^-y
= -(y + 2) e^-y + c
x = -(y + 2) + c. e^y

ప్రశ్న 5.
x(x – 1)\(\frac{d y}{d x}\) – y = x³(x – 1)³
సాధన:

ప్రశ్న 6.
(x + 2y³)\(\frac{d y}{d x}\) = y
సాధన:

ప్రశ్న 7.
(1 – x²)\(\frac{d y}{d x}\) + 2xy = x\(\sqrt{1-x^2}\)
సాధన:

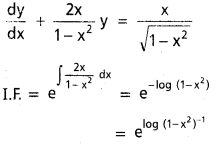
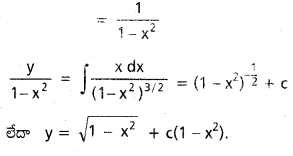
ప్రశ్న 8.
x(x – 1)\(\frac{d y}{d x}\) – (x – 2)y = x³(2x – 1)
సాధన:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) – \(\frac{x-2}{x(x-1)} y\) = \(\frac{x^3(2 x-1)}{x(x-1)}\)
I.F. = \(e^{\int \frac{2-x}{x(x-1)}} d x\)
\(\frac{2-x}{x(x-1)}\) = \(\frac{A}{x}\) + \(\frac{B}{x-1}\)
2 – x = A(x – 1) + B.x
x = 0 ⇒ 2 = -A ⇒ A = -2
x = 1 ⇒ 1 – B ⇒ B = 1

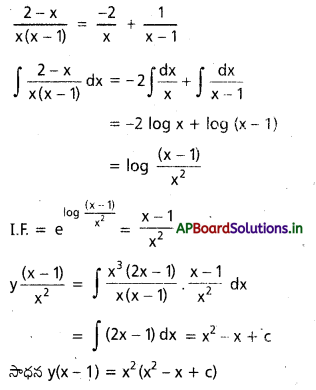
ప్రశ్న 9.
\(\frac{d y}{d x}\)(x²y³ + xy) = 1 (Mar. ’11)
సాధన:
\(\frac{d x}{d y}\) =xy + x²y³
ఇది బెర్నౌలీ సమీకరణము
x^-2. \(\frac{d x}{d y}\) – \(\frac{1}{x} \cdot y\) = y³
z = \(-\frac{1}{x}\) అనుకొంటే \(\frac{\mathrm{dz}}{\mathrm{dy}}\) = \(\frac{1}{x^2} \frac{d x}{d y}\)

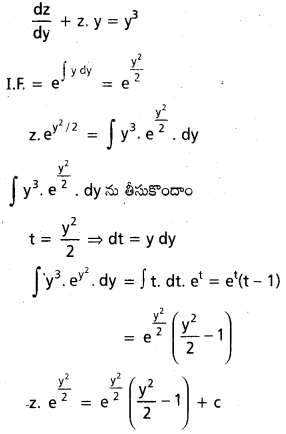
ప్రశ్న 10.
\(\frac{d y}{d x}\) + x sin 2y = x³ cos² y
సాధన:

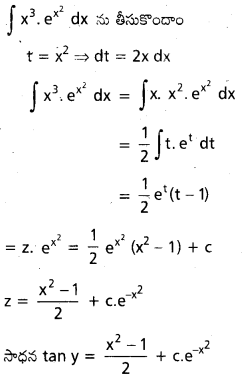
ప్రశ్న 11.
y² + (x – \(\frac{1}{y}\))\(\frac{d y}{d x}\) = 0
సాధన: