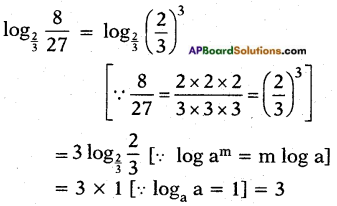AP SSC 10th Class Maths Solutions Chapter 1 Real Numbers InText Questions

AP State Syllabus SSC 10th Class Maths Solutions 1st Lesson Real Numbers InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 1 Real Numbers InText Questions and Answers.

10th Class Maths 1st Lesson Real Numbers InText Questions and Answers

Do this

Question 1.
Find q and r for the following pairs of positive integers a and b, satisfying a = bq + r. (Page No. 3)
i) a = 13, b = 3
Answer:
13 = 3 × 4 + 1
here q = 4 ; r = 1
ii) a = 8, b = 80
Answer:
Take a = 80, b = 8
80 = 8 × 10 + 0 here q = 10 ; r = 0
iii) a = 125, b = 5
Answer:
125 = 5 × 25 + 0
here q = 25 ; r = 0
iv) a = 132, b = 11
Answer:
132 = 11 × 12 + 0
here q = 12 ; r = 0

Question 2.
Find the HCF of the following by using Euclid division lemma,
i) 50 and 70 (Page No. 4)
Answer:
For given two positive integers a > b;
there exists unique pair of integers q and r satisfying a = bq + r; 0≤r<b.
∴ 70 = 50 × 1 + 20
Here a = 70, b = 50, q = 1, r = 20.
Now consider 50, 20
50 = 20 × 2 + 10
Here a = 50, b = 20, q = 2, r = 10.
Now taking 20 and 10.
20 = 10 × 2 + 0
Here the remainder is zero.
∴ 10 is the HCF of 70 and 50.

ii) 96 and 72
Answer:
96 = 72 × 1 + 24
72 = 24 × 3 + 0
∴ HCF = 24

iii) 300 and 550
Answer:
550 = 300 × 1 + 250
300 = 250 × 1 + 50
250 = 50 × 5 + 0
∴ HCF = 50

iv) 1860 and 2015
Answer:
2015 = 1860 × 1 + 155
1860 = 155 × 12 + 0
∴ HCF = 155

Think & Discuss

Question 1.
From the above questions in ‘DO THIS’, what is the nature of q and r? (Page No. 3)
Answer:
Given: a = bq + r
q > 0 and r lies in between 0 and b
i.e. q > 0 and 0 ≤ r < b

Question 2.
Can you find the HCF of 1.2 and 0.12? Justify your answer. (Page No. 4)
Answer:
Given: 1.2 and 0.12
we have 1.2 = \(\frac{12}{10}\) = \(\frac{120}{100}\)
0.12 = \(\frac{12}{100}\)
Now considering the numerators 12 and 120, their HCF is 12.
∴ HCF of 1.2 and 0.12 is \(\frac{12}{100}\) = 0.12
i.e., if x is a factor of y then x is the HCF of x and y.

Question 3.
If r = 0, then what is the relationship between a, b and q in a = bq + r of Euclid divison lemma? (Page No. 6)
Answer:
Given: r = 0 in a = bq + r then a = bq
i.e., b divides a completely.
i.e., b is a factor of a.

Do this

Question 1.
Express 2310 as a product of prime factors. Also see how your friends have factorized the number. Have they done it as you ? Verify your final product with your friend’s result. Try this for 3 or 4 more numbers. What do you conclude? (Page No. 7)
Answer:
Given: 2310
2310 = 2 × 1155
= 2 × 3 × 385
= 2 × 3 × 5 × 77
2310 = 2 × 3 × 5 × 7 × 11

We notice that this prime factorization is unique.
And also notice that prime factorization of any number is unique i.e., every composite number can be expressed as a product of primes and this factorization is unique.
E.g: 144 = 2 × 72
= 2 × 2 × 36
= 2 × 2 × 2 × 18
= 2 × 2 × 2 × 2 × 9
= 2 × 2 × 2 × 2 × 3 × 3
= 24 × 32
320 = 2 × 160
= 2 × 2 × 80
= 2 × 2 × 2 × 40
= 2 × 2 × 2 × 2 × 20
= 2 × 2 × 2 × 2 × 2 × 10
= 2 × 2 × 2 × 2 × 2 × 2 × 5
= 26 × 5
125 = 5 × 25
= 5 × 5 × 5
= 5³

Question 2.
Find the HCF and LCM of the following given pairs of numbers by prime factorization, (Page No. 8)
i) 120, 90
Answer:
We have 120 = 2 × 2 × 2 × 3 × 5
= 2³ × 3 × 5
90 = 2 × 3 × 3 × 5
= 2 × 3² × 5

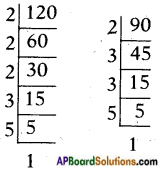
∴ HCF = 2 × 3 × 5 = 30
LCM = 2³ × 3² × 5 = 360

ii) 50, 60
Answer:
We have
50 = 2 × 5 × 5 = 2 × 5²
60 = 2 × 2 × 3 × 5 = 2² × 3 × 5

∴ HCF = 2 × 5 = 10
LCM = 2² × 3 × 5² = 300

iii) 37, 49
Answer:
We have
37 = 1 × 37
49 = 7 × 7 = 7²
∴ HCF = 1
LCM = 37 × 7²
Note: H.C.F. of two relatively prime numbers is 1 and LCM is equal to product of the numbers.

Try this

Question 1.
Show that 3ⁿ × 4^m cannot end with the digit 0 or 5 for any natural numbers ‘n’ and’m’. (Page No. 8)
Answer:
Given number is 3⁴ × 4^m.
So the prime factors to it are 3 and 2 only.
I: but if a number want to be end with zero it should have 2 and 5 as its prime factors, but the given hasn’t ‘5’ as its prime factor.
So it cannot be end with zero.
II : now if a number went to be end with 5 it should have ‘5’ as its one of prime factors. But given 3ⁿ × 4^m do not have 5 as a factor.
So it cannot be end with 5.
Hence proved.

Do this

Question 1.
Write the following terminating decimals in the form of p/q, q ≠ 0 and p, q are co-primes.
i) 15.265
ii) 0.1255
iii) 0.4
iv) 23.34
v) 1215.8
What can you conclude about the denominators through this process? (Page No. 10)
Answer:
i) 15.265

ii) 0.1255

iii) 0.4
0.4 = \(\frac{4}{10}\) = \(\frac{2}{5}\)
iv) 23.34

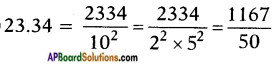
v) 1215.8

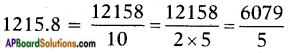
Two and five are the factors for the denominator.

Question 2.
Write the following rational numbers in the form of p/q, where q is of the form 2ⁿ.5^m where n, m are non-negative integers and then write the numbers in their decimal form. (Page No. 11)
i) \(\frac{3}{4}\)
ii) \(\frac{7}{25}\)
iii) \(\frac{51}{64}\)
iv) \(\frac{14}{25}\)
v) \(\frac{80}{100}\)
Answer:
i) \(\frac{3}{4}\)
\(\frac{3}{4}\) = \(\frac{3}{2 \times 2}\) = \(\frac{3}{2^{2}}\)

Decimal form of \(\frac{3}{4}\) = 0.75

ii) \(\frac{7}{25}\)
\(\frac{7}{25}\) = \(\frac{7}{5 \times 5}\) = \(\frac{7}{5^{2}}\)

Decimal form of \(\frac{7}{25}\) = 0.28

iii) \(\frac{51}{64}\)
\(\frac{51}{64}\) = \(\frac{51}{2^{6}}\)
[∵ 64 = 2 × 32
= 2² × 16
= 2³ × 8
= 2⁴ × 4 = 2⁵ × 2 = 2⁶]

Decimal form of \(\frac{51}{64}\) = 0.796875

iv) \(\frac{14}{25}\)

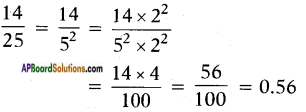
v) \(\frac{80}{100}\)
\(\frac{80}{100}\) = \(\frac{80}{2^{2} \times 5^{2}}\) = \(\frac{80}{10^{2}}\) = 0.80

Question 3.
Write the following rational numbers as decimal form and find out the block of repeating digits in the quotient. (Page No. 11)
i) \(\frac{1}{3}\)
ii) \(\frac{2}{7}\)
iii) \(\frac{5}{11}\)
iv) \(\frac{10}{13}\)
Answer:
i) \(\frac{1}{3}\)
\(\frac{1}{3}\) = 0.3333…. = \(0 . \overline{3}\)
Block of digits, repeating in the quotient = period = 3.

ii) \(\frac{2}{7}\)
Decimal form of \(\frac{2}{7}\) = 0.285714….
Repeating part/period = 285714
∴ \(\frac{2}{7}\) = \(0 . \overline{285714}\)

iii) \(\frac{5}{11}\)
Period = 45
Decimal form of \(\frac{5}{11}\) = 0.454545.
= \(0 . \overline{45}\)

iv) \(\frac{10}{13}\)
Decimal form of \(\frac{10}{13}\) = 0.769230.
= \(0 . \overline{769230}\)
Period = 769230

Do this

Question 1.
Verify the statement proved above for p = 2, p = 5 and for a² = 1, 4, 9, 25, 36, 49, 64 and 81. (Page No. 14)
Answer:


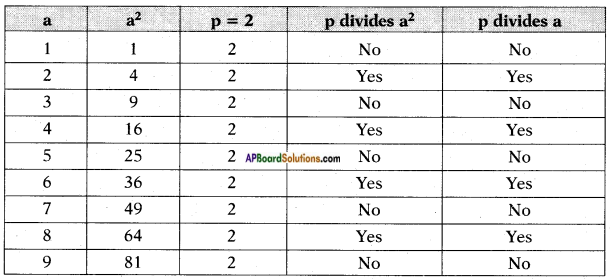
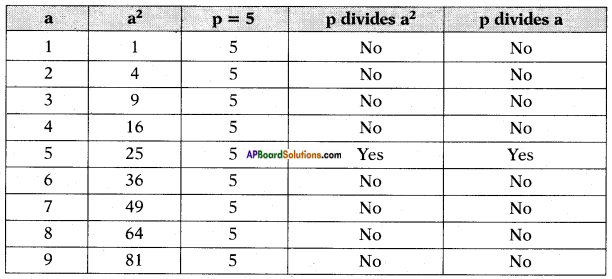
From the above we can conclude that if a prime number ‘p’ divides a², then it also divides a.

Think and Discuss

Question 1.
Write the nature of y, a and x in y = a^x. Can you determine the value of x for a given y? Justify your answer. (Page No. 17)
Answer:
y = a^x here a ≠ 0
We can determine the value of ‘x’ for a given y.
for example y = 5, a = 2
We cannot express y = a^x for y = 5, a = 2 and for y = 7, a = 3, we cannot express seven (7) as a power of 3.

Question 2.
You know that 2¹ = 2, 4¹ = 4, 8¹ = 8 and 10¹ = 10. What do you notice about the values of log₂ 2, log₄ 4, log₈ 8 and log₁₀ 10? What can you generalise from this?  (Page No. 18)
Answer:
From the graph log₂ 2 = log₄ 4 = log₈ 8 = log₁₀ 10 = 1
We conclude that log_a a = 1 where a is a natural number.

Question 3.
Does log₁₀ 0 exist? (Page No. 18)
Answer:
No, log₁₀ 0 doesn’t exist, i.e a^x ≠ 0 ∀ a, x ∈ N.

Question 4.
We know that, if 7 = 2^x then x = log₂ 7. Then what is the value of \(2^{\log _{2} 7}\)? Justify your answer. Generalise the above by taking some more examples for \(\mathbf{a}^{\log _{\mathrm{a}} \mathbf{N}}\). (Page No. 21)
Answer:
We know that if 7 = 2^x then x = log₂ 7
We want to find the value of \(2^{\log _{2} 7}\);
Now put log₂ 7 = x in the given
∴ \(2^{\log _{2} 7}\) = 2^x = 7 (given)
∴ \(2^{\log _{2} 7}\) = 7
Thus \(\mathbf{a}^{\log _{\mathrm{a}} \mathbf{N}}\) = N

a) \(3^{\log _{3} 8}\)
Answer:
If x = \(3^{\log _{3} 8}\) then
log₃ x = log₃ 8
⇒ x = 8

b) \(5^{\log _{5} 10}\)
Answer:
If y = \(5^{\log _{5} 10}\)
then log₅ y = log₅ 10
⇒ y = 10

Do this

Question 1.
Write the powers to which the bases to be raised in the following.  (Page No. 18)
i) 64 = 2^x
Answer:
64 = 2^x
We know that
64 = 2 × 32
= 2 × 2 × 16
= 2 × 2 × 2 × 8
= 2 × 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2 × 2
64 = 2⁶
⇒ x = 6

ii) 100 = 5^b
Answer:
Here also 100 cannot be written as any power of 5.
i.e., there exists no integer for b such that 5^b = 100

iii) \(\frac{1}{81}\) = 3^c
Answer:
We know that 81 = 3 x 27
= 3 × 3 × 9
= 3 × 3 × 3 × 3
= 34
∴ \(\frac{1}{81}\) = 3^-4   [∵ a^-m = \(\frac{1}{\mathrm{a}^{\mathrm{m}}}\)]
∴ c = – 4

iv) 100 = 10^z
Answer:
100 = 10²
z = 2

v) \(\frac{1}{256}\) = 4^a
Answer:
We know that 256 = 4 × 64
= 4 × 4 × 16
= 4 × 4 × 4 × 4
∴ \(\frac{1}{256}\) = 4^-4
∴ a = – 4

Question 2.
Express the logarithms of the following into sum of the logarithms.   (Page No. 19)
i) 35 × 46
Answer:
log xy = log x + log y
log₁₀35 × 46 = log₁₀35 + log₁₀46

ii) 235 × 437
Answer:
log₁₀235 × 437 = log₁₀235 + log₁₀437   [∵ log xy = log x + log y]

iii) 2437 × 3568
Answer:
log₁₀ 2437 × 3568 = log₁₀2437 + log₁₀3568   [∵ log xy = log x + log y]

Question 3.
Express the logarithms of the follow¬ing into difference of the logarithms.   (Page No. 20)
i) \(\frac{23}{34}\)
Answer:
log₁₀ = \(\frac{23}{34}\) = log₁₀ 23 – log₁₀ 34
[∵ log \(\frac{x}{y}\) = log x – log y]

ii) \(\frac{373}{275}\)
Answer:
log₁₀ = \(\frac{373}{275}\) = log₁₀ 373 – log₁₀ 275
[∵ log \(\frac{x}{y}\) = log x – log y]

iii) \(\frac{4525}{3734}\)
Answer:
log₁₀ = \(\frac{4525}{3734}\) = log₁₀ 4525 – log₁₀ 3734
[∵ log \(\frac{x}{y}\) = log x – log y]

iv) \(\frac{5055}{3303}\)
Answer:
log₁₀ = \(\frac{5055}{3303}\) = log₁₀ 5055 – log₁₀ 3303
[∵ log \(\frac{x}{y}\) = log x – log y]

Question 4.
By using the formula log_axⁿ = n log_a x, convert the following.   (Page No. 21)
i) log₂ 7²⁵
Answer:
log₂ 7²⁵ = 25 log₂ 7

ii) log₅ 8⁵⁰
Answer:
log₅ 8⁵⁰ = 50 log₅ 8 = 50 log₅ 23
= 3 × 50 log₅2 = 150 log₅2

iii) log 5²³
Answer:
log 5²³ = 23 log 5

iv) log 1024
Answer:
log 1024 = log 2¹⁰ [∵ 1024 = 2¹⁰]
= 10 log 2

Try this

Question 1.
Write the following relation in exponential form and find the values of respective variables.   (Page No. 18)
i) log₂32 = x
Answer:
log₂32 = x
⇒ log₂2⁵ = x     [∵ 32 = 2⁵]
⇒ 5 log₂2 = x     [∵ log a^m = m log a]
⇒ 5 × 1 = x      [∵ log_a a = 1]
∴ x = 5

ii) log₅625 = y
Answer:
log₅625 = y
⇒ log₅4 = y    [∵ 625 = 5⁴]
⇒ 4 log₅ 5 = y     [∵ log a^m = m log a]
⇒ 4 × 1 = y     [∵ log_a a = 1]
∴ y = 4

iii) log₁₀10000 = z
Answer:
log₁₀10000 = z
=> log₁₀10⁴ = z     [∵ 10000 = 10 × 10 × 10 × 10 = 10⁴]
=> 4 log₁₀10 = z     [∵ log a^m = m log a]
=> 4 × 1 = z     [∵ log_a a = 1]
∴ z = 4

iv) \(\log _{7} \frac{1}{343}\) = -a
Answer:

Question 2.
i) Find the value of log₂32. (Page No. 21)
Answer:
log₂ 32 = log₂ 2⁵
[∵ 32 = 2 × 2 × 2 × 2 × 2 = 2⁵]
= 5 log₂ 2 [∵ log a^m = m log a]
= 5 × 1 [∵ log_a a = 1]
= 5

ii) Find the value of log_c √c.
Answer:

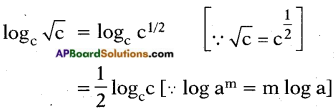
= \(\frac{1}{2}\) × 1 [∵ log_a a = 1]
= \(\frac{1}{2}\)

iii) Find the value of log₁₀0.001
Answer:

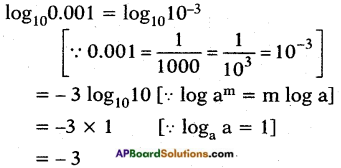
iv) Find the value of \(\log _{\frac{2}{3}} \frac{8}{27}\)
Answer: