SCERT AP 8th Class Biology Study Material Pdf 1st Lesson విజ్ఞానశాస్త్రం అంటే ఏమిటి? Textbook Questions and Answers.
AP State Syllabus 8th Class Biology 1st Lesson Questions and Answers విజ్ఞానశాస్త్రం అంటే ఏమిటి?
8th Class Biology 1st Lesson విజ్ఞానశాస్త్రం అంటే ఏమిటి? Textbook Questions and Answers
I. విషయావగాహన
ప్రశ్న 1.
విజ్ఞానశాస్త్రం అందించిన కొన్ని ఆధునిక ఫలితాలు తెలపండి.
జవాబు:
- విజ్ఞానశాస్త్రం మానవుని సుఖమయ జీవనానికి అనేక వస్తువులు, వసతులు అందించినది.
- కంప్యూటర్లు, మొబైల్ ఫోన్లు, ఇంటర్నెట్, అంతరిక్ష నౌకలు, సంకరజాతి ఆహారధాన్యాలు, రొబోటిక్స్, వైద్యం ఈ కోవలోనికి వస్తాయి.
ప్రశ్న 2.
విజ్ఞానశాస్త్రం అంటే ఏమిటి ?
జవాబు:
మనచుట్టూ ఉన్న ప్రాకృతిక ప్రపంచం ఎలా పనిచేస్తుందో తెలుసుకోవడానికి దాని పూర్వాపరాలను అవగాహన చేసుకోవడానికీ అందుబాటులో ఉన్న సౌకర్యాలతో, ఆధారాలతో మనం చేసే ప్రయత్నాలను అన్నింటినీ కలిపి విజ్ఞానశాస్త్రం (Science) అంటారు.
ప్రశ్న 3.
చాలా సందర్భాలలో శాస్త్రవేత్తలు ఇంతకు ముందు కనుగొన్న అంశాల మీదనే తిరిగి ప్రయోగాలు చేస్తుంటారు. ఇలా ఎందుకు చేస్తుంటారు ? ఉదహరించండి.
జవాబు:
- కొత్త ఆలోచనలను పరీక్షించుకోవడానికి ప్రయత్నించడం లేదా పాత భావనలను తోసిపుచ్చడం ద్వారా కొత్త విషయాలను కనుగొనవచ్చు.
- దీనివల్ల శాస్త్రవేత్తలు విజ్ఞానశాస్త్ర చరిత్రలో స్థానం సంపాదించిన వారవుతారు.
- ఇలా కనుగొన్న నూతన భావనలు మన ఆలోచనా విధానాన్ని మార్చేస్తాయి.
- ఉదాహరణకు నెప్ట్యూనను మనం ఇంతకాలం వరకు గ్రహంగా గుర్తించాం కాని నూతన పరిశోధనలు అది గ్రహం కాదని నిర్ధారించాయి.
- అలాగే కడుపులో అల్సర్లకు ఆహారపు అలవాట్లు, వ్యాకులత కారణమని అనుకుంటుండేవాళ్ళం. కానీ దీనికి బ్యాక్టీరియా కారణమని నేడు కనుగొన్నారు.
![]()
ప్రశ్న 4.
శాస్త్రవేత్తలకు సమాజం బోలెడన్ని వనరులను ఎందుకు సమకూర్చుతుంది ?
జవాబు:
- శాస్త్రవేత్తల పరిశోధనలు సామాన్య మానవులు మంచి జీవితం గడపటానికి దోహదం చేస్తాయి.
- సమాజం ఎదుర్కొంటున్న అనేక సమస్యలకు శాస్త్రవేత్తలు పరిష్కారం చూపుతారు.
- శాస్త్ర ఆవిష్కరణలు మానవ జీవితాన్ని మరింత సుఖమయం చేస్తాయి.
- శాస్త్ర పరిశోధనలు మానవ జీవితాన్ని ఆధునీకరిస్తాయి.
అందుచేత సమాజం శాస్త్రవేత్తలకు వనరులను సమకూర్చుతుంది.
ప్రశ్న 5.
శాస్త్రవేత్తలు సమాజం కోసం తమ జీవితాలను త్యాగం చేయటానికి ప్రేరేపించే అంశం ఏమిటి ?
జవాబు:
- శాస్త్రవేత్తలు ప్రజల జీవన విధానం మెరుగుపర్చాలనే తపన కలిగి ఉంటారు.
- సమస్యను పరిష్కరించటం వలన శాస్త్రవేత్తలు తృప్తి పొందుతారు.
- సాధారణంగా శాస్త్రవేత్తలు అన్వేషణ దృక్పథం కలిగి ఉంటారు. వారు పనిలో ఆనందం పొందుతారు.
- దీని వలన వారు పరిశోధనల కొరకు జీవితాలను త్యాగం చేయగలరు.
ప్రశ్న 6.
ప్రజల ఆర్థిక స్థితిగతులను అభివృద్ధి చేయటంలో శాస్త్రవేత్తల పాత్ర ఏమిటి ?
జవాబు:
ప్రజల ఆర్థిక స్థితిగతులను అభివృద్ధి చేయడం. దీని కోసం చాలామంది శాస్త్రవేత్తలు ప్రకృతి వనరులైన పెట్రోలియం, ఖనిజాలను కనుగొనడం లేదా పునరుత్పత్తి చేయడంలో సరైన, సమర్థవంతమైన మార్గాల కోసం అన్వేషిస్తారు. వృక్ష శాస్త్రవేత్తలు కొత్త జాతుల పంటలు, పండ్ల మొక్కలు కనుగొనడం ద్వారా తక్కువ ధరల్లో పోషకాహారం అందించి ఆరోగ్యవంతమైన జాతిని రూపొందించడానికి ప్రయత్నిస్తారు.
ప్రశ్న 7.
ఈ కింది పదాలను నిర్వచించండి.
ఎ) శాస్త్రీయ పద్ధతి
బి) శాస్త్రీయ ప్రక్రియా నైపుణ్యాలు
సి) విజ్ఞాన శాస్త్రం
జవాబు:
ఎ) శాస్త్రీయ పద్ధతి : శాస్త్రవేత్తలు గుర్తించిన సమస్యలకు, ప్రశ్నలకు కొన్ని క్రమపద్ధతులు వినియోగిస్తారు. వీటినే శాస్త్రీయ పద్ధతులు అంటారు.
బి) శాస్త్రీయ ప్రక్రియా నైపుణ్యాలు : శాస్త్రీయ పద్ధతిలో వాడే ప్రణాళికను అర్థం చేసుకోవడానికి కొన్ని నైపుణ్యాలు అవసరం. వీటిని శాస్త్రీయ ప్రక్రియా నైపుణ్యాలు అంటారు.
ఉదా : సేకరణ, నిర్వహణ, విశ్లేషణ మొదలగునవి.
సి) విజ్ఞాన శాస్త్రం : ప్రకృతిలో దాగివున్న రహస్యాలను, నిజాలను, కారణాలను తెలుసుకోవడానికి ఉపయోగపడే చక్కటి, స్పష్టమైన మార్గాన్ని ‘విజ్ఞాన శాస్త్రం’ అంటారు.
![]()
ప్రశ్న 8.
శాస్త్రీయ పద్ధతిలో వున్న సోపానాలను పేర్కొనండి.
జవాబు:
శాస్త్రీయ పద్ధతిలో ఈ క్రింది సోపానాలు కలవు. అవి
- ప్రశ్నించటం
- పరికల్పన చేయటం
- ప్రణాళిక చేయటం
- ప్రయోగం నిర్వహించటం
- ఫలితాలను ప్రదర్శించటం
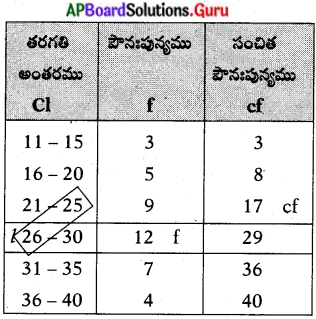
ప్రశ్న 9.
శాస్త్రీయ పద్ధతిలోని సోపానాలను ఉదాహరణలతో వివరించండి.
జవాబు:
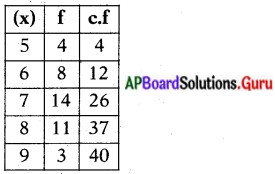
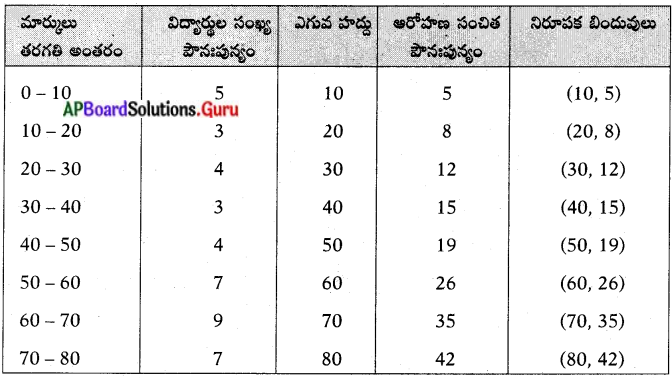
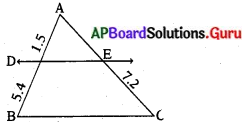
| సోపానాలు | వివరణ | ఉదాహరణ |
| 1. పరిశీలన | వస్తువు, సంఘటనలను గురించి నేర్చు కోవడంలో జ్ఞానేంద్రియాలను వాడటం. | ఉదా : విత్తనాలు నేలలో మొలకెత్తుతాయి. కానీ ఏ నేల విత్తనాలు మొలకెత్తటానికి అనుకూలం? |
| 2. పరికల్పన | ఒక సమస్యకు సమాధానాలు ఊహించటం | తోట నేలలో గింజలు బాగా మొలకెత్తుతాయని అనుకొంటున్నాను. |
| 3. ప్రయోగం కోసం ప్రణాళిక | పరికల్పనను నిరూపించటానికి ప్రయోగ విధానాన్ని రూపొందించుకోవటం. | మూడు వేరు వేరు నేలలలో ఒకే రకం విత్తనాలు నాటి, పరిశీలించాలి. |
| 4. ప్రయోగ నిర్వహణ | ప్రణాళిక ప్రకారం చరరాశులను నియంత్రిస్తూ ప్రయోగం చేయటం. ఫలితాలను నమోదుచేయటం. | మూడు కుండీలలో వేరు వేరు మట్టి తీసుకొని విత్తనాలు నాటి, నీరు పోశాను. 21 రోజుల తరువాత అన్ని మొక్కల పొడవు కొలిచాను. |
| 5. నిర్ధారించటం | ప్రయోగ ఫలిత సమాచారాన్ని విశ్లేషించి పరికల్పన సరైనదా కాదా అని నిర్ణయించడం. | ప్రయోగంలో ఇసుకమట్టి, తోట మట్టిలో మొక్కలు బాగా పెరిగాయి. బంకమట్టిలో విత్తనాలు మొలకెత్తలేదు. |
![]()
ప్రశ్న 10.
నీకు తెలిసిన ఏవైనా ఐదు ప్రక్రియా నైపుణ్యాలు రాయండి.
జవాబు:
శాస్త్రీయ పద్ధతిలో వాడే కొన్ని పనులే ప్రక్రియా నైపుణ్యాలు. అవి :
- కొలవటం
- సేకరించటం
- నమోదు చేయటం
- ప్రదర్శించటం
- ఊహించటం
ప్రశ్న 11.
పరికల్పన అనగానేమి?
జవాబు:
పరీక్షించటానికి వీలున్న సాధ్యమయ్యే సమాధానాన్ని పరికల్పన అంటారు.
ఉదా : బండి ఆగిపోయినపుడు పెట్రోలు అయిపోయి ఉండవచ్చు అని భావించుట.
ప్రశ్న 12.
‘చరరాశులు’ అనగానేమి?
జవాబు:
‘పరిశోధనా ఫలితాన్ని ప్రభావితంచేసే అంశాలను చరరాశులు అంటారు. చరరాశులన్ని నియంత్రించటం వలన కచ్చితమైన ఫలితాలు పొందవచ్చు.
ప్రశ్న 13.
అన్వేషణా పద్ధతిలోని సోపానాలను ఉదాహరణతో వివరించండి.
జవాబు:
సమస్యను పరిష్కరించటంలో పాటించే క్రమమైన పద్ధతులను అన్వేషణా పద్ధతి అంటారు. దీనిలో ఈ క్రింది సోపానాలు ఉంటాయి.
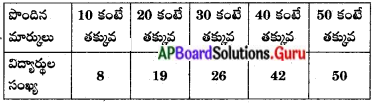
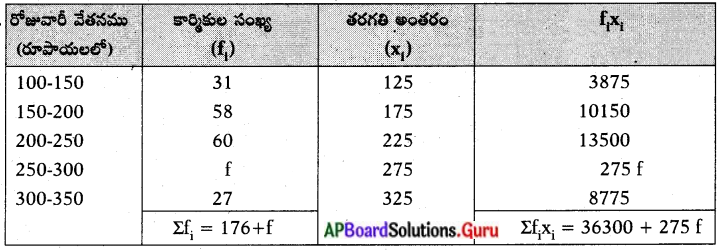
| సోపానము | ఉదాహరణ |
| 1. సమస్యను గుర్తించటం | గదిలో లైటు వెలగకపోవటం |
| 2. పరికల్పనలు చేయటం |
|
| 3. సమాచారాన్ని సేకరించటం | టెస్టర్, స్మూడైవర్, ఇన్సులేషన్, టేప్, కరెంట్ తీగలు, బ్లేడు, చెక్కస్కేలు, సేకరించుకోవటం |
| 4. సమాచారాన్ని విశ్లేషించటం | సేకరించిన వస్తువులను ప్రయోగాలకు, పరిశీలనకు అమర్చుకోవటం |
| 5. ప్రయోగాలు చేయటం |
|
| 6. ఫలితాల విశ్లేషణ | ఫిలమెంట్ కాలిపోలేదు బాగానే ఉంది కాబట్టి ఫ్యూజ్ పరిశీలించాలి. ఫ్యూజ్ వైరు తెగిపోయి ఉంది. కాబట్టి ఫ్యూజ్ తీగను మార్చాలి. తీగను మార్చినపుడు బల్బు వెలిగింది. |
| 7. నిర్ధారణకు రావటం | ఫ్యూజ్ పోవటం వలన బల్బు వెలగలేదు. |
![]()
II. ప్రశ్నించటం, పరికల్పన చేయటం
ప్రశ్న 1.
ప్రభుత్వం శాస్త్రవేత్తలకు బోలెడన్ని వనరులు ఇచ్చి ప్రజలు ఎదుర్కొంటున్న సమస్యలకు పరిష్కారం చూపాలని అడగటం సమంజసమేనా ? వివరించండి.
జవాబు:
- ప్రజల జీవన విధానాన్ని మెరుగుపరచటానికి ప్రతి శాస్త్రవేత్త తపిస్తాడు.
- దీని కోసం వారు తమ జీవితాలను సైతం త్యాగం చేస్తారు.
- దీని ద్వారా అనేక కొత్త అంశాలు కనుగొనబడ్డాయి.
- దీనితో ప్రజల స్థితిగతులు మెరుగుపడ్డాయి.
- ఈ పరిశోధనా ఫలితాలు మానవాళి ఉన్నతికి చాలా ఉపయోగపడతాయి.
- ఆహార ఉత్పత్తి అభివృద్ధి, జన్యు సమాచారం, సునామీ, తుపానులను ముందే గ్రహించే అవకాశం కలిగింది.
- అందువల్ల ప్రభుత్వం శాస్త్రవేత్తలకు వనరులను అందించటం సమంజసమే అని నా అభిప్రాయం.
ప్రశ్న 2.
కార్ల్ పాపర్ మాటల్లో “సరిదిద్దబడ్డ తప్పుల చరిత్రనే సైన్స్” అంటారు. దీనిని నీవు ఎలా సమర్ధిస్తావు ?
జవాబు:
- విజ్ఞానశాస్త్రం నిత్య నూతనంగా ఉంటుంది.
- ఈ రోజు ఆవిష్కరణ రేపటి కొత్త ఆలోచనలకు పునాది అవుతుంది.
- ఏ శాస్త్రవేత్త కూడా ఇదే అసలు పరిష్కారం అని భావించరు.
- దీని కన్నా మంచి ‘సౌకర్యం’ మరింత సౌలభ్యంగా ఉంటుందనుకుంటారు.
- ప్రస్తుత పరిశోధనలో తప్పులు సరిచేసుకుంటూ మంచి ఫలితం కోసం ప్రయత్నం చేస్తారు.
ఉదా : 19వ శతాబ్దం మొదట్లో బస్సు గరిష్ఠ వేగం గంటకు 20 కి.మీ. నుండి 30 కి.మీ. మాత్రమే. కానీ ఇప్పుడు వొల్వో బస్సు వేగం గంటకు 300 నుండి 360 కి.మీ. ఇది శాస్త్ర ప్రగతికి మంచి ఉదాహరణ. - బస్సు ఇంజనులో ఉన్న చిన్న చిన్న సమస్యలను సరిచేసుకుంటూ ఈనాటి బస్సులను అభివృద్ధి చేసారు.
- అందువల్ల నేను కార్ల్ పాపర్ మాటలను సమర్ధిస్తాను.
ప్రశ్న 3.
వివిధ శాస్త్రవేత్తలు చేసే పనులు, వారి పేర్లు తెలుసుకోవటానికి ఎటువంటి ప్రశ్నలు అడుగుతారు ?
1. ఖగోళ శాస్త్రవేత్త అని ఎవరిని అంటారు ?
జవాబు:
ఆకాశంలోని నక్షత్రాలు, గ్రహాల సమాచారం తెలిపేవారు.
2. భూగర్భ శాస్త్రవేత్త అని ఎవరిని అంటారు ?
జవాబు:
శిలాజాలు, ఖనిజాలు గురించి చెప్పేవారు.
3. జీవుల ప్రవర్తన గురించి ఎవరు అధ్యయనం చేస్తారు ?
జవాబు:
పర్యావరణ శాస్త్రవేత్త
![]()
ప్రశ్న 4.
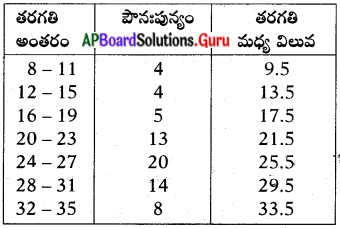
ఈ కింద ఇవ్వబడిన శాస్త్ర విభాగాన్ని చదివి, అవి పరిశీలించే అంశాలు రాయండి.
| వ.సం. | శాస్త్ర విభాగం | పరిశీలించే అంశం |
| 1. | వృక్షశాస్త్రం | |
| 2. | సిస్మాలజీ | |
| 3. | శిలాజ శాస్త్రం | |
| 4. | మానవ శాస్త్రం | |
| 5. | శరీర ధర్మశాస్త్రం | |
| 6. | వాతావరణ శాస్త్రం |
జవాబు:
| వ.సం. | శాస్త్ర విభాగం | పరిశీలించే అంశం |
| 1. | వృక్షశాస్త్రం | మొక్కల నిర్మాణం, పెరుగుదల వ్యాధులు మొ॥ |
| 2. | సిస్మాలజీ | భూకంపాల గురించి |
| 3. | శిలాజ శాస్త్రం | వృక్ష, జంతు సంబంధ శిలల గురించి చెప్పేది. |
| 4. | మానవ శాస్త్రం | ప్రాచీన, ఆధునిక మానవుల జీవన విధానాలు. |
| 5. | శరీర ధర్మశాస్త్రం | జీవుల శరీర నిర్మాణాలు, అవి పని చేసే విధానాలు. |
| 6. | వాతావరణ శాస్త్రం | వాతావరణంలోని గతులు-మార్పులు గురించి తెలిపేది. |
![]()
III. ప్రయోగాలు, క్షేత్ర పరిశీలనలు
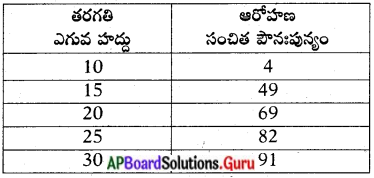
ప్రశ్న 1.
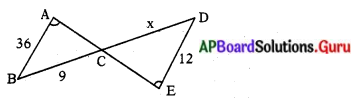
చరిత రాయి ఆకృతి పరిమాణంలో మార్పునకు గల కారణాలు ఎలా కనుగొన్నది ?
జవాబు:
- చరిత మూడు రాళ్ళను సేకరించింది.
- వాటి ద్రవ్యరాశులను కొలిచింది.
- ఈ రాళ్లను నీరు, ఇసుక గల గ్లాసులో ఉంచింది.
- రోజూ ఒకసారి ఊపుతూ ఒక వారం రోజుల పాటు చేసింది.
- వారం తర్వాత ఆమె రాళ్లు, ఇసుక, జాడి ద్రవ్యరాశులను కొలిచింది. వచ్చిన సమాచారాన్ని విశ్లేషించింది.
- రాళ్లు ఇసుకతో రుద్దడం వల్ల అవి పెచ్చులుగా విడిపోతాయని నిర్ధారించింది.
ప్రశ్న 2.
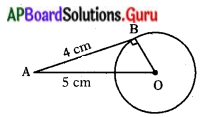
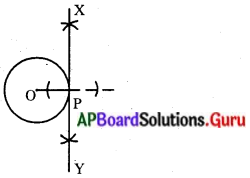
‘స్విచ్’ పనిచేసే విధానాన్ని నీవు ఎలా తెలుసుకొంటావు ?
జవాబు:
- బ్యాటరీ, తీగెలు, బల్బుతో ఒక విద్యుత్ వలయం ఏర్పర్చాను.
- ఒక డ్రాయింగ్ బోర్డుమీద రెండు డ్రాయింగ్ పిన్నులు గుచ్చి దానికి విద్యుత్ తీగలు కలిపాను.
- రెండు పిన్నుల మధ్య లోహపు తీగె ఉంచినపుడు వలయం పూర్తిఅయి బల్బు వెలిగింది.
- లోహపు తీగెను తీసినపుడు వలయం తెరుచుకొని బల్బు ఆరిపోయింది.
- బల్బును ఆర్పటానికి, వెలిగించటానికి లోహపుతీగె స్విచ్ లా పనిచేసింది.
ప్రశ్న 3.
ఏ తువ్వాలు ఎక్కువ నీటిని పీల్చుకుంటుందో ఎలా నిర్ధారిస్తావు ?
జవాబు:
- ఈ ప్రయోగానికి నేను మూడు రకాల టవల్స్ ఎన్నుకొన్నాను.
- మూడు బీకర్లు తీసుకొని, ఒక్కొక్కదానిలో ఒక లీటరు నీరు పోశాను.
- మూడు రకాల టవలను వేరు వేరు బీకర్లలో 10 సెకండ్ల పాటు ఉంచాను.
- నీటి నుండి టవలను తీసి ప్రక్కన ఉంచాను.
- బీకరులో మిగిలిన నీటిని గమనిస్తే ఏ టవల్ ఎక్కువ నీటిని పీల్చుకున్నదో అర్థమైనది.
![]()
ప్రశ్న 4.
మీ ఇంటిలోని వంటగదిలో ఉన్న ఆలుగడ్డను వారం రోజులు పరిశీలించి, నీ పరిశీలనలను నమోదు చేయండి.
జవాబు:
| పరిశీలన | |
| మొదటి రోజు |
|
| రెండవ రోజు | అక్కడక్కడా మొగ్గలు నెమ్మదిగా పెరుగుతుండటం గమనించాను. |
| నాల్గవ రోజు | గుంతల్లా వున్న భాగాల నుంచి సన్నని కాడ మరియు చిన్న చిన్న ఆకులు రావటం గమనించాను. |
| ఉపాధ్యాయుడు : గుంతలున్న భాగాన్ని కోసి మరలా నాటితే ఏమవుతుందో చూడండి ! | |
| ఎనిమిదవ రోజు | అది కొత్త మొక్కగా అభివృద్ధి చెందిందని గమనించాను. “వీటిని కాండ మొగ్గలు” అంటారు. ఇవి రూపాంతరం చెందాయి. |
ప్రశ్న 5.
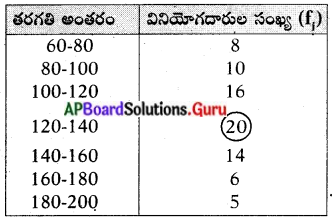
మీ గ్రామ జనాభా వివరాలు సేకరించి కమ్మీ చిత్రాల ద్వారా దానిని ప్రదర్శించండి.
జవాబు:
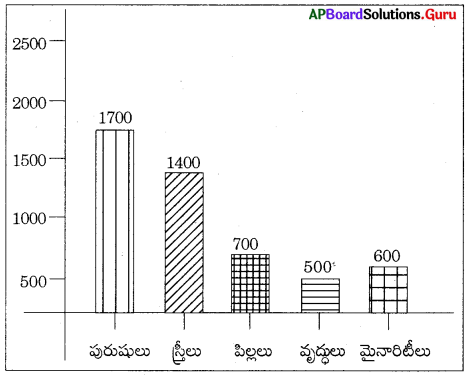
పురుషులు – 1700
స్త్రీలు – 1400
పిల్లలు – 700
వృద్ధులు – 500
మైనారిటీలు – 600
![]()
IV. సమాచార సేకరణ నైపుణ్యాలు, ప్రాజెక్ట్ పనులు
ప్రశ్న 1.
మీ బడిలోని ప్రయోగశాలను చూసి దానిలో మీరు తీసుకున్న భద్రతా వివరాలు రాయండి.
జవాబు:
- మా పాఠశాలలో ఉన్న ప్రయోగశాలను మా సైన్సు ఉపాధ్యాయులు నిర్వహిస్తారు.
- పెద్ద హాలు వంటి నిర్మాణంలో సగం జీవశాస్త్ర సంబంధ నమూనాలు, చార్టులు మొ॥నవి, రెండవ సగంలో భౌతిక, రసాయన శాస్త్రానికి సంబంధించిన పరికరాలు ఉన్నాయి.
- భద్రత పరంగా మా ప్రయోగశాల సురక్షితమైనది. ఎందుకంటే –
- ప్రయోగశాలలో నీటి సౌకర్యం ఉంది. దీనితో ప్రయోగ అనంతరం చేతులు, పరికరాలు శుభ్రంగా కడుక్కోవచ్చు.
- తగిన సంఖ్యలో పెద్ద కిటికీలు ఉన్నాయి. దీని ద్వారా తగిన గాలి, వెలుతురు ప్రయోగశాలలో ఉంటుంది.
- ప్రయోగశాలలో మేమందరం క్రమశిక్షణతో, నిశ్శబ్దంగా ఉంటాం.
- మా సైన్సు మాష్టారి అనుమతి లేనిదే ఏమీ ముట్టుకోము. ఇది భద్రత పరంగా ఎంతో ముఖ్యం.
- ప్రయోగ సమయంలో మా ఉపాధ్యాయులు చెప్పిన భద్రతా సూత్రాలు తప్పక పాటిస్తాం.
- తలుపులు, కిటికీలు బయటకు తెరుచుకునేలా మా ప్రధానోపాధ్యాయులు జాగ్రత్త తీసుకున్నారు.
దీనివల్ల ఏదైనా అనుకోని సంఘటన జరిగితే మేమందరం సురక్షితంగా బయటపడవచ్చు.
ప్రశ్న 2.
నీ స్నేహితులు శాస్త్ర విషయాలు చదివేటప్పుడు ఎదుర్కొనే సమస్యలపై ప్రాజెక్టు పనిని చేయండి.
జవాబు:
సమస్య : లలిత్, అభయ్ లు శాస్త్ర విషయాలు చదివేటప్పుడు కొన్ని సమస్యలు ఎదుర్కొంటున్నారు. అవి :
- అవగాహన త్వరగా జరగటంలేదు.
- శాస్త్రీయ పదాలు గుర్తుండటం లేదు.
దీనిపై వారు వారి మిత్రుడు శ్రావణ్ ను సంప్రదించారు.
ప్రాథమిక సమాచారం :
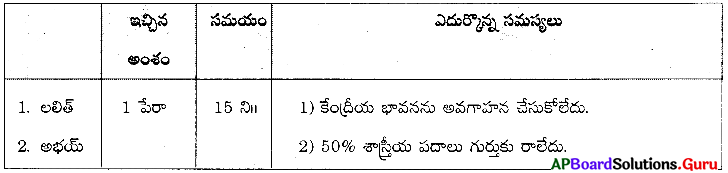
దీన్ని విశ్లేషించి ఈ కింది సూచనలు చేశారు.
- ఇచ్చిన అంశాన్ని బిగ్గరగా చదవటం.
- దానిలోని శాస్త్రీయ పదాలను 5 లేదా 10సార్లు (imposition) రాయటం.
పై విధంగా 10 రోజులు సాధన తరువాత ద్వితీయ సమాచారం సేకరించడమైనది.

![]()
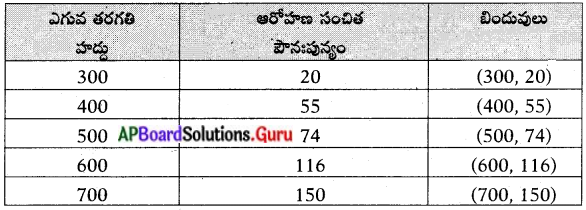
ప్రశ్న 3.
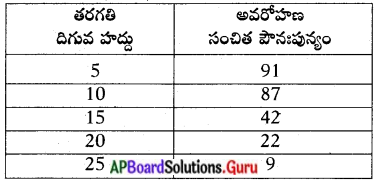
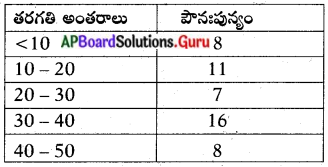
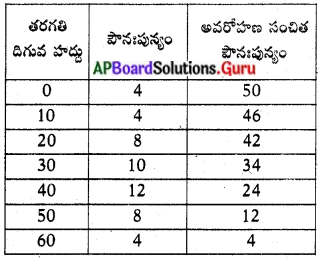
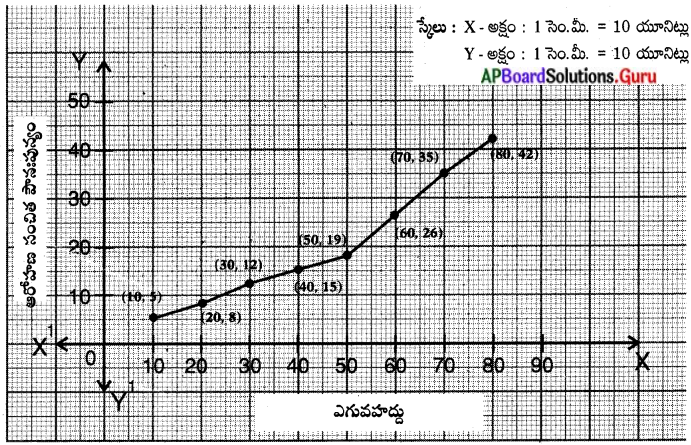
ప్రక్క ‘బార్ గ్రాఫ్’ ను పరిశీలించి మీరు గ్రహించిన సమాచారం తెలపండి.
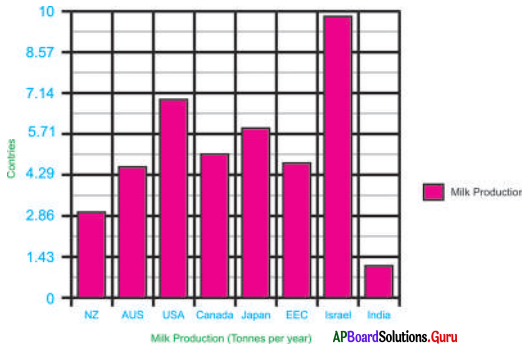
జవాబు:
- ఈ బార్ గ్రాఫ్. వివిధ దేశాలలోని పాల ఉత్పత్తిని తెలుపుతుంది.
- పాల ఉత్పత్తిలో ఇజ్రాయెల్ అగ్రస్థానంలో ఉంది.
- ఇజ్రాయెల్ తరువాత, అమెరికా, జపాన్ ద్వితీయ, తృతీయ స్థానాలలో కొనసాగుతున్నాయి.
- పాల ఉత్పత్తిలో భారతదేశం గణనీయంగా వెనుకబడి ఉంది.
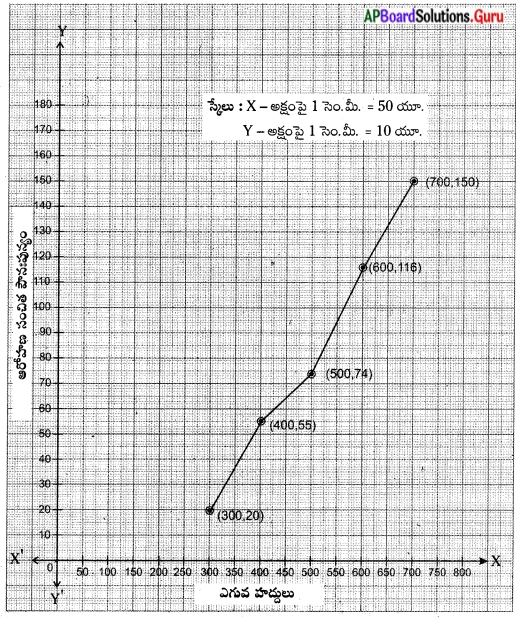
ప్రశ్న 4.
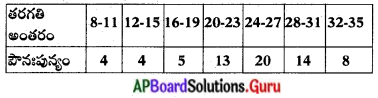
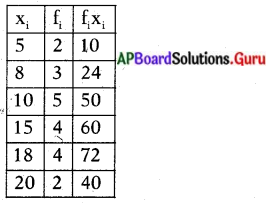
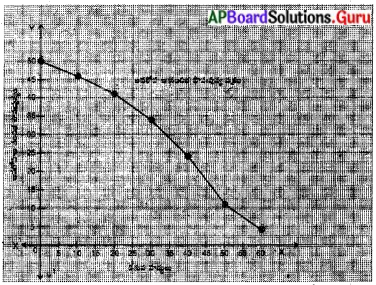
ప్రక్క గ్రాఫ్ నుండి నీవు గమనించిన అంశాలు ఏమిటి?
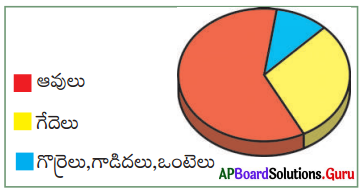
జవాబు:
- పై చార్టు వివిధ జంతువుల పాల వినియోగం తెలుపుతుంది.
- మనం, ఆవులు, గేదెలు, గొర్రెలు, గాడిదలు, ఒంటెల గేదెలు నుండి పాలు వినియోగిస్తున్నాం.
- పాల వినియోగంలో అధిక శాతం ఆవుల నుండి లభిస్తుంది.
- ఆవుల తరువాత, గేదెల పాల ‘మీద మనం అధికంగా ఆధారపడ్డాము.
- గొర్రె, ఒంటె పాలను తక్కువ మంది జనాభా వినియోగిస్తున్నారు.
V. బొమ్మలు గీయడం, నమూనాలు తయారుచేయడం
ప్రశ్న 1.
పరిశోధనా ప్రణాళికలోని సోపానాలను ప్రవాహ పటం ద్వారా చూపుము.
జవాబు:
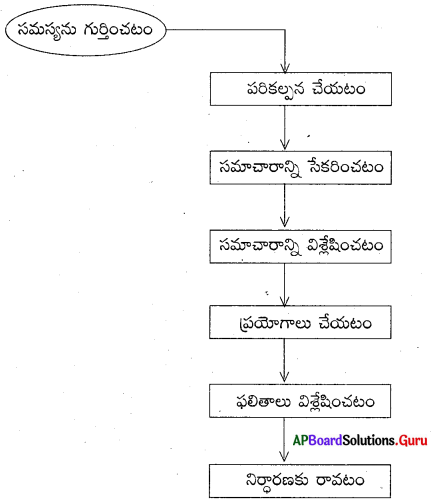
![]()
VI. అభినందించటం, సౌందర్యాత్మక స్పృహ కలిగి ఉండటం, విలువలు పాటించడం
ప్రశ్న 1.
శాస్త్రవేత్తల కృషిని మీరు చదివినప్పుడు ఎలాంటి అనుభూతి పొందారు ?
జవాబు:
- శాస్త్రవేత్తలు ప్రకృతిని పరిశీలించి, వాటిని నమోదు చేసి, విశ్లేషించి ప్రకృతి నియమాలను విపులంగా అర్థం చేసుకుంటారు.
- ఈ క్రమంలో ఎన్నో నూతన ఆవిష్కరణలు చేస్తారు.
- అవి మానవాళికి వారి జీవన విధానం మెరుగుపరచుకోవటానికి ఎంతో దోహదపడుతుందని అర్థం అయినప్పుడు, ఎంతో సంతోషం, ఉత్తేజంగా అనిపిస్తుంది.
- కానీ ఈ అన్వేషణలో వారు తమ జీవితాలను ప్రయోగశాలలకే అంకితం చేస్తారు. వారి త్యాగం వెల కట్టలేనిది.
- ఉదా : ఐన్ స్టీన్ ను అతని వ్యక్తిగత వైద్యుడు పరీక్షించి “మీరు బాగా అలసిపోతున్నారు. కాబట్టి మీ మనసుకు హాయి అనిపించే ప్రదేశానికి వెళ్ళండి” అని చెప్తే, ఐన్ స్టీన్ మరలా తన ప్రయోగశాలకే వెళ్ళాడు. దీనిని చదివినప్పుడు శాస్త్రవేత్తలు పడే శ్రమ, తపన అర్థం అవుతుంది. మనం కూడా భవిష్యత్తులో మంచి శాస్త్రవేత్త అవుదామని అనిపిస్తుంది.
ప్రశ్న 2.
శాస్త్రాభివృద్ధి మానవ జీవితంలో తెచ్చిన మార్పులను నీవు ఎలా అభినందిస్తావు ?
జవాబు:
- అనాగరికంగా, ఆదిమానవుడులా సంచరించే మానవుడు శాస్త్ర విజ్ఞానం వలన ఆధునిక మానవుడుగా అవతరించాడు.
- నిప్పును కనుగొని ప్రకృతి శక్తులను తన చేతులలోనికి తీసుకోవటం ప్రారంభించాడు.
- తరువాత కనుగొన్న చక్రం మానవ జీవితాన్ని ప్రగతి బాటన నడిపింది.
- దీని వలన రోడ్డు రవాణా సౌకర్యాలు ప్రారంభమయ్యాయి.
- ఆధునిక ఆవిష్కరణలో కంప్యూటర్ ఒక అద్భుత పరికరం.
- ఇది ఇంటర్నెట్ ద్వారా ప్రపంచాన్ని కుగ్రామంగా మార్చింది.
- రోదసి యాత్రలు, మానవ పరిధిని భూగోళం దాటించాయి.
- నేడు మనం వాడుతున్న అన్ని పరికరాలూ శాస్త్ర విజ్ఞానం వల్లనే లభించాయి.
ఈ సౌకర్యవంత జీవనానికి శాస్త్రరంగాన్ని అభినందిద్దాము.
![]()
VII. నిజజీవిత వినియోగం, జీవ వైవిధ్యం పట్ల సానుభూతి కలిగి ఉండటం
ప్రశ్న 1.
నిజ జీవితంలో నీకు పనికి వస్తున్న శాస్త్ర విజ్ఞాన విషయాలను, వస్తువులను పట్టిక రూపంలో రాయండి.
జవాబు:
| వ.సం. | వస్తువు పేరు | తెలుసుకోదగిన అంశం |
| 1. | ఉల్లిగడ్డ |
|
| 2. | కరివేపాకు | వేరు మొగ్గలకు ఉదాహరణ |
| 3. | నిమ్మరసం |
|
| 4. | బెలూన్లు | గాలి అన్నివైపులా ఒత్తిడిని సమంగా కలిగిస్తుందని తెలుసుకోవటం. |
| 5. | అగ్గిపుల్లలు | నానబెట్టి, పొరలు తీసి సూక్ష్మదర్శిని సాయంతో కణాల అన్వేషణ |
ప్రశ్న 2.
సైన్సు ప్రయోగశాలలో పాటించే జాగ్రత్తలు ఏమిటి ?
జవాబు:
పాటించాల్సిన జాగ్రత్తలు :
- ముందుగా ఆలోచించండి : పరిశోధనలోని సోపానాలను అధ్యయనం చేయటం వలన మీరు ఏమి ఆశిస్తున్నారో తెలుసుకోవచ్చు. మీరు ఏవైనా ప్రశ్నలను అడగాలనుకుంటే ఉపాధ్యాయుడిని అడగండి. మీకు చూపించిన భద్రత గుర్తులను బాగా అవగాహన చేసుకోండి.
- శుభ్రంగా ఉండండి : మీరు పనిచేసే ప్రాంతం శుభ్రంగా ఉంచండి. మీకు పొడవైన వెంట్రుకలుంటే వెనుకకు నెట్టండి. ముందుకు పడకుండా చూసుకోండి. పొడవైన చొక్కా చేతులను మడుచుకోండి. లేకపోతే ప్రయోగం నిర్వహించేటప్పుడు జుట్టు లేదా చొక్కా చేతులు తగిలి పదార్థాలు ఒలికిపోవచ్చు.
- అడగండి : మీరు ఏదైనా పారేయాలన్నా, పగలగొట్టాలన్నా, కత్తిరించాలన్నా మీ ఉపాధ్యాయునికి తప్పని సరిగా చెప్పండి.
- మీ కళ్ళు జాగ్రత్త : భద్రతనిచ్చే కళ్లజోళ్లను వాడండి. మీ కళ్ళలో ఏమైనా పడితే మీ ఉపాధ్యాయునికి వెంటనే చెప్పండి.
- రుచి చూడవద్దు : సైన్స్ కృత్యాలు నిర్వహించేటప్పుడు మీ ఉపాధ్యాయుని అనుమతి లేకుండా ఏ పదార్థాన్ని త్రాగకండి, తినకండి.
- షాక్ నుండి దూరంగా ఉండండి : విద్యుత్ పరికరాలు ఉపయోగించేటప్పుడు జాగ్రత్త పడండి. విద్యుత్ పరికరాలను భద్రంగా ఉంచండి. విద్యుత్ ప్రవాహానికి ఆటంకం కలగకుండా ప్లగ్గులు, వైర్లు ఉపయోగించండి. ప్లగ్గులు పెట్టేటప్పుడు, తీసేటప్పుడు జాగ్రత్తగా ఉండండి.
- శుభ్రంగా ఉంచండి : పని ముగించిన వెంటనే ప్రయోగ బల్లను శుభ్రంగా ఉంచండి. అన్ని వస్తువులు ఎక్కడివి అక్కడ సర్ది పెట్టండి. మీరు పనిచేసే ప్రాంతాన్ని తుడవండి. మీ చేతులు కడుక్కోండి.