AP 10th Class Maths Important Questions Chapter 14 సాంఖ్యక శాస్త్రం

These AP 10th Class Maths Chapter Wise Important Questions 14th Lesson సాంఖ్యక శాస్త్రం will help students prepare well for the exams

AP Board 10th Class Maths 14th Lesson Important Questions and Answers సాంఖ్యక శాస్త్రం

ప్రశ్న 1.
5, 3, 4, – 4, 6, 7, 0 దత్తాంశ మధ్యగతము ఎంత?
సాధన.
ఇవ్వబడిన పరిశీలనాంశములు 5, 3, 4, – 4, 6, 7, 0.
పరిశీలనాంశములను ఆరోహణ క్రమంలో వ్రాయగా – 4, 0, 3, 4, 5, 6, 7.
మొత్తము 7 పరిశీలనాంశములున్నవి. కనుక \(\frac{7+1}{2}\) = 4వ పరిశీలనాంశము మధ్యగతమగును.
∴ మధ్యగతము = 3.

ప్రశ్న 2.
5, 6, 9, 6, 12, 3, 6, 11, 6, 7 ల బాహుళకం ఎంత ?
సాధన.
5, 6, 9, 6, 12, 3, 6, 11, 6, 7 లలో 6 యొక్క పౌనఃపున్యము గరిష్టం కావున పై దత్తాంశానికి బాహుళకం = 6.

ప్రశ్న 3.
మొదటి n సహజ సంఖ్యల సగటు కనుగొనుము.
సాధన.
సగటు = మొదటి ‘n’ సహజ సంఖ్యల మొత్తం / n
= \(\frac{\Sigma \mathrm{n}}{\mathrm{n}}=\frac{\mathrm{n}(\mathrm{n}+1)}{2} \cdot \frac{1}{\mathrm{n}}=\left[\frac{\mathrm{n}+1}{2}\right]\)
∴ మొదటి ‘n’ సహజ సంఖ్యల సగటు = \(\frac{n+1}{2}\)

ప్రశ్న 4.
వర్గీకృత దత్తాంశము యొక్క అంకగణితపు సగటు \(\bar{x}=a+\frac{\sum f_{1} d_{i}}{\Sigma f_{i}}\) అయిన f_i మరియు d_i పదాలు వేటిని సూచిస్తాయి ?
సాధన.
f_i = తరగతి పౌనఃపున్యం
d_i = విచలనము = x_i – a

ప్రశ్న 5.
5, 6, 9, 10, 6, 12, 3, 6, 11, 10 ల దత్తాంశపు సగటు ఎంత ?
సాధన.
దత్తాంశం సగటు = ఇచ్చిన రాశుల మొత్తం / ఇచ్చిన రాశుల సంఖ్య
= \(\frac{5+6+9+10+6+12+3+6+11+10}{10}\)
= \(\frac{78}{10}\) = 7.8.

ప్రశ్న 6.
క్రింది దత్తాంశానికి ఆరోహణ సంచిత మరియు అవరోహణ సంచిత పౌనఃపున్య పట్టికలు వ్రాయండి.

సాధన.
ఆరోహణ సంచిత పౌనఃపున్య పట్టిక

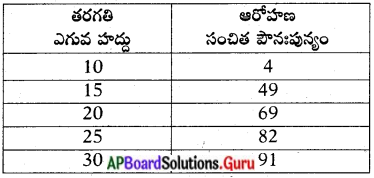
అవరోహణ సంచిత పౌనఃపున్య పట్టిక

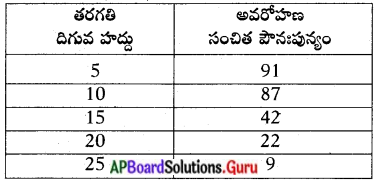
ప్రశ్న 7.
క్రింది పౌనఃపున్య విభాజన. పట్టికకు మధ్య విలువలు • వ్రాయండి.

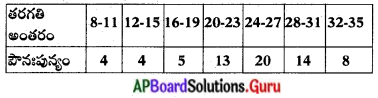
సాధన.

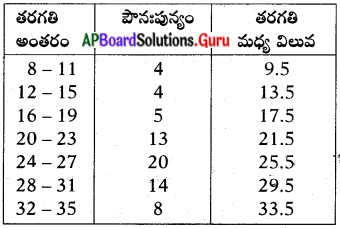
ప్రశ్న 8.
క్రింది దత్తాంశమునకు మధ్యగతమును కనుగొనుము.

సాధన.

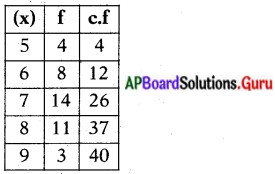
n = 40
మధ్యగతము = \(\frac{n+1}{2}=\frac{40+1}{2}=\frac{41}{2}\) = 20.
5వ పదము = 7.

ప్రశ్న 9.
ఈ క్రింది దత్తాంశమునకు తరగతి అంతరములను ఉపయోగించి పౌనఃపున్య విభాజన పట్టికను తయారు చేయుము. .

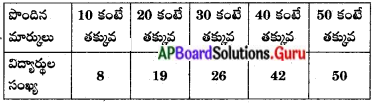
సాధన.

ప్రశ్న 10.
క్రింది దత్తాంశం యొక్క అంకమధ్యమాన్ని కనుగొనండి.

సాధన.

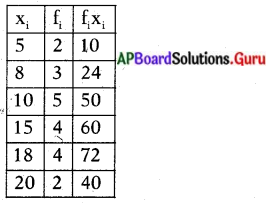
Σf_ix_i = 256; Σf_i = 20
అంకమధ్యమం = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{256}{20}\) = 12.8.

ప్రశ్న 11.
క్రింది దత్తాంశమునకు బాహుళకము కనుగొనండి.

సాధన.

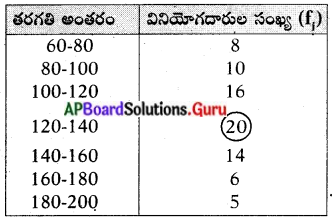
ఎక్కువ మంది వినియోగదారులు 120 – 140.
తరగతికి చెందినవారు కనుక బాహుళకపు తరగతి. 120 – 140.
బాహుళకపు తరగతి దిగువహద్దు (l) = 120
తరగతి పరిమాణము (h) = 20
బాహుళకపు తరగతి పౌనఃపున్యం (f₁) = 20
బాహుళకపు తరగతికి పూర్వపు తరగతి పౌనఃపున్యం (f₀) = 16.
బాహుళకపు తరగతికి తర్వాత పౌనఃపున్యం (f₂) = 14.
సూత్రమునుపయోగించి,
బాహుళకము = l + \(\left[\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{2 \mathrm{f}_{1}-\mathrm{f}_{0}-\mathrm{f}_{2}}\right]\) × h

= 120 + \(\left[\frac{20-16}{2 \times 20-16-14}\right]\) × 20

= 120 + \(\left[\frac{4}{40-30}\right]\) × 20

= 120 + \(\left[\frac{4}{10}\right]\) × 20
= 120 + 8 = 128.

ప్రశ్న 12.
క్రింది దత్తాంశానికి “అవరోహణ సంచిత పౌనఃపున్య వక్రం” గీయండి.

సాధన.
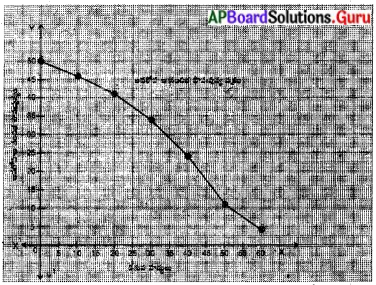
అవరోహణ సంచిత పౌనఃపున్య వక్రం

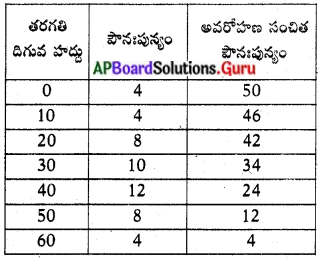
X- అక్షంపై దిగువ హద్దులు, మరియు Y – అక్షంపై అవరోహణ సంచిత పౌనఃపున్యం గుర్తించుము.

X- అక్షంపై 1 సెం.మీ. = 5 యూ.
Y – అక్షంపై 1 సెం.మీ. = 5 యూ.

ప్రశ్న 13.
క్రింది దత్తాంశమునకు బాహుళకము కనుక్కోండి. ”

సాధన.

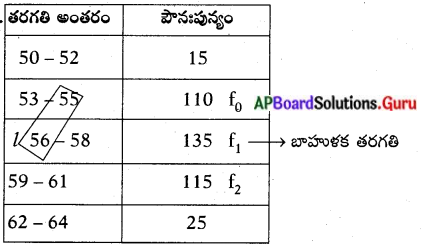
బాహుళకము = l + \(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\) × h;
l = 55.5; f₀ = 110; f₁ = 135; f₂ = 115; h = 3

బాహుళకము = 55.5 + \(\frac{25}{270-225}\) × 3

= 55.5 + \(\frac{25}{45}\) × 3

= 55.5 + \(\frac{5}{3}\) × 3

= 55.50 + 1.67 = 57.17.

ప్రశ్న 14.
దిగువనీయబడిన దత్తాంశమునకు ‘మధ్యగతము’ కనుగొనండి.

సాధన.

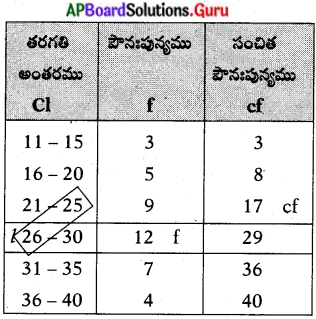
n = 40, \(\frac{n}{2}\frac{40}{2}\) = 20
l = 25.5, f = 12, cf = 17, h = 5
మధ్యగతము = l + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
= 25.5 + (\(\frac{20-17}{12}\)) × 5
= 25.5 + (\(\frac{3}{12}\) × 5)
= 25.50 + \(\frac{5}{4}\)
= 25.50 + 1.25 = 26.75.

ప్రశ్న 15.
ఈ క్రింది పట్టికను, ఆరోహణ సంచిత పౌనఃపున్య పట్టికగా మార్చి దానినుపయోగించి ‘ఓజివ్’ వక్రమును గ్రాఫ్ ద్వారా చూపుము.

సాధన.

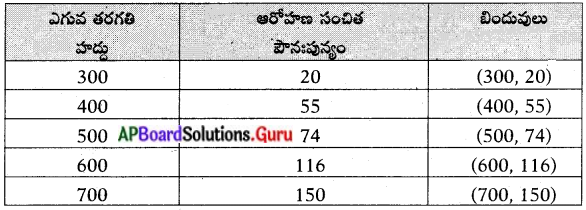
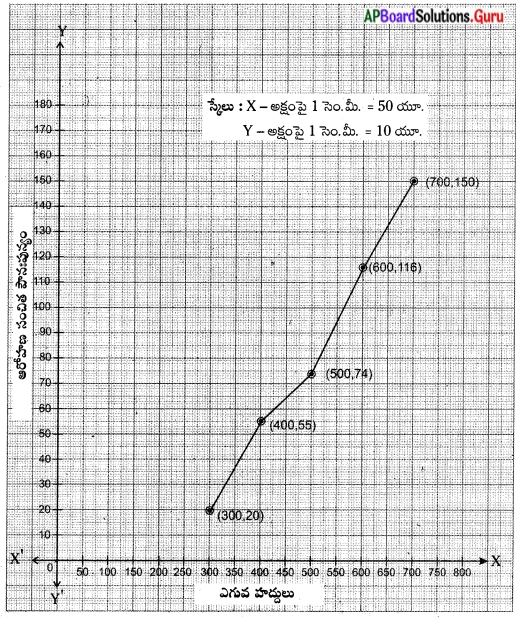
ప్రశ్న 16.
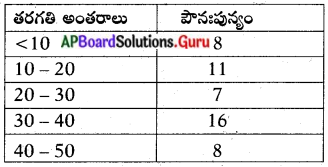
క్రింద ఇవ్వబడిన పట్టికలో 25 కుటుంబాలు ఆహారానికి వెచ్చించే దినసరి ఖర్చులు ఇవ్వబడినవి. ఆ దత్తాంశానికి బాహుళకంను కనుగొనండి.

సాధన.

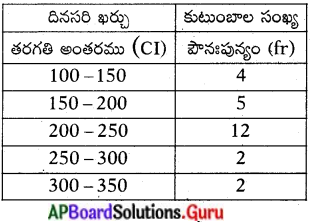
భాహుళకము = l + \(\left(\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{2 \mathrm{f}_{1}-\mathrm{f}_{0}-\mathrm{f}_{2}}\right)\) × h

‘l’ = బాహుళక తరగతి దిగువ హద్దు = 200
‘f₁‘ – బాహుళక తరగతి పౌనఃపున్యం = 12
‘f₀‘ – బాహుళక తరగతికి ముందున్న ఉన్న తరగతి పౌనఃపున్యం = 5
‘f₂‘ – బాహుళక తరగతికి తరువాత ఉన్న తరగతి పౌనఃపున్యం = 2
‘h’ – బాహుళక తరగతి పొడవు = 50 200-250 250-300
∴ బాహుళకము = 200 + (\(\frac{12-5}{24-5-2}\)) × 50
= 200 + \(\frac{7 \times 50}{17}\)
= 200 + \(\frac{350}{17}\)
= 200 + 20.58
∴ బాహుళకము = 220.58.

ప్రశ్న 17.
ఒక పరీక్షలో 53 మంది విద్యార్థులకు వచ్చిన మార్కులు క్రింది పట్టికలో ఇవ్వబడినవి. ఆ దత్తాంశానికి “ఆరోహణ సంచిత పౌనఃపున్య వక్రం”ను గీయండి.

సాధన.

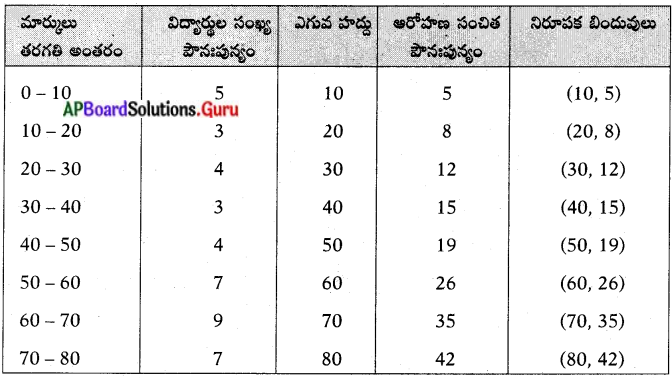
ఆరోహణ సంచిత పౌనఃపున్య ఓజీవ్ వక్రం గీయుట కొరకు X-అక్షంపై తరగతి ఎగువ హద్దును, Y-అక్షంపై ఆరోహణ సంచిత పౌనఃపున్యమును తీసుకొనవలెను.

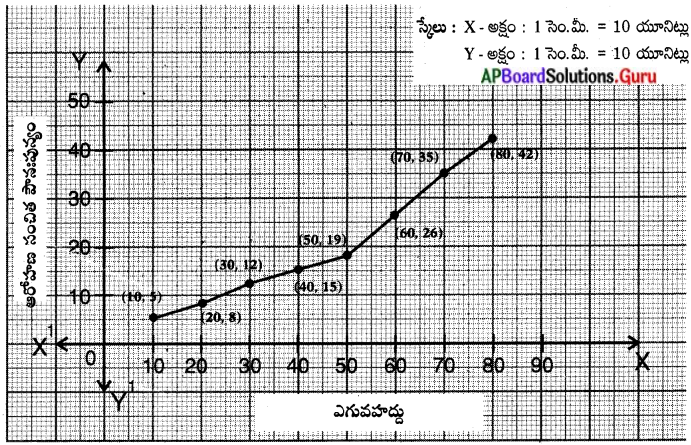
ప్రశ్న 18.
ఒక వాణిజ్య సంస్థ యందు కార్మికుల రోజువారీ వేతనములు క్రింది పౌనఃపున్య విభాజనము నందు ఇవ్వబడినవి. ఈ విభాజనము యొక్క సగటు ₹ 220. అయితే ఇందు లోపించిన పౌనఃపున్యం f ను కనుగొనుము.

సాధన.

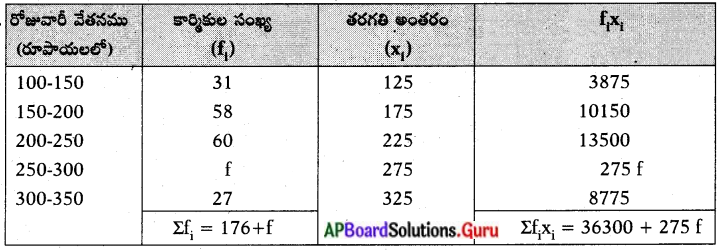
ఇచ్చినది, x_i = 220
\(\overline{\mathrm{X}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{X}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\)
⇒ 220 = \(\frac{36300+275 \mathrm{f}}{176+\mathrm{f}}\)
⇒ 220(176 + f) = 36300 + 275f
⇒ 38720 + 220 f = 36300 + 275 f
⇒ 220 f – 275 f = 36300 – 38720
⇒ – 55 f = – 2420
⇒ f = \(\frac{2420}{55}\) = 44.