Mahesh

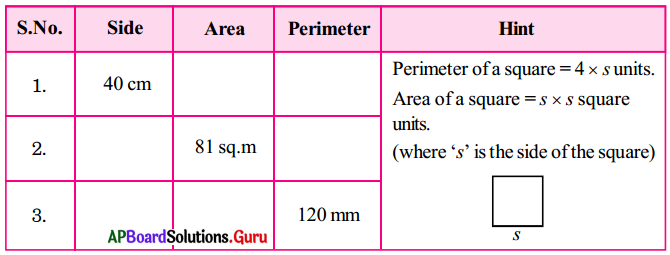
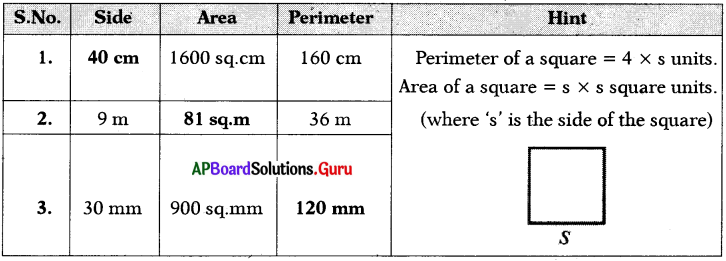
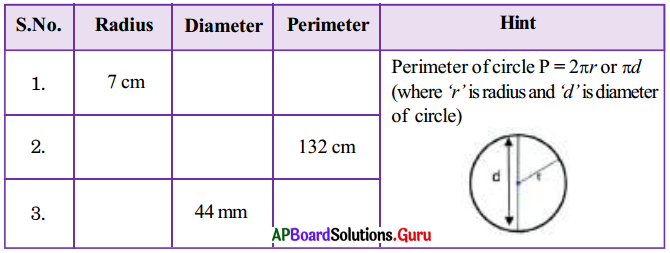
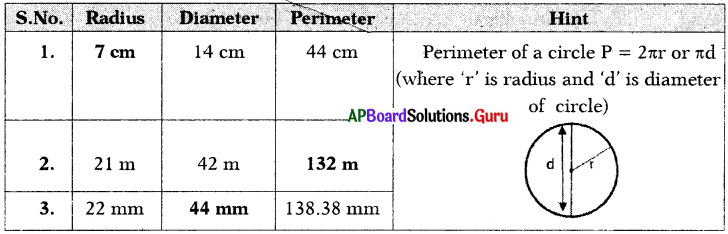
These AP 7th Class Science Important Questions 2nd Lesson Nature of Substances will help students prepare well for the exams.

AP Board 7th Class Science 2nd Lesson Important Questions and Answers Nature of Substances

Question 1.
From which language does the word ‘Acid’ derived?
Answer:
The word acid came from the Latin word ‘acere’ means sour.

Question 2.
Give some examples for substances containing acids.
Answer:
Tamarind, Lemon, Tomato, Apple, Curd, Raw mango etc.

Question 3.
What is the chemical name of vitamin C?
Answer:
The chemical name of vitamin C is Ascorbic acid.

Question 4.
Name some substance in which vitamin C is available.
Answer:
Vitamin C is available in citrus fruits and in amla (usiri).

Question 5.
What will happen when carbon dioxide is added to water?
Answer:
When carbon dioxide is added to water, it become carbonic acid/soda.

Question 6.
How are bases to touch?
Answer:
Bases are slippery to touch.

Question 7.
Which base is used to prepare bath soap?
Answer:
Bath soap is prepared using potassium hydroxide.

Question 8.
Which base is used to prepare detergent soap?
Answer:
Detergent soap for washing clothes is prepared using Sodium hydroxide.

Question 9.
What are the main components in the tooth paste?
Answer:
Main components in the tooth paste are calcium carbonate, aluminum hydroxide and sodium bi carbonate. All these chemicals are bases.

Question 10.
What are alkalis?
Answer:
Bases that can dissolve in water are called alkalis.

Question 11.
Give some examples for alkalis.
Answer:
Some examples of alkalis are sodium hydroxide, potassium hydroxide and calcium hydroxide.

Question 12.
What are neutral substances?
Answer:
The substance which is neither an acid nor a base is known as neutral substance.

Question 13.
Give examples for neutral substances.
Answer:
Distilled water, salt solution, sugar solution etc are example for neutral substances.

Question 14.
Who gave the most modern definition of acids and alkalis?
Answer:
Svante Arrhenius Swedish physical chemist gave the most modern definition of acids and alkalis.

Question 15.
What are indicators?
Answer:
Substances which are used to test acids or bases are called acid base indicators.

Question 16.
From what does litmus extracted?
Answer:
Litmus is extracted from lichens.

Question 17.
What are olfactory indicators?
Answer:
Substances which change their smell when mixed with acid or base are known as olfactory indicators. Ex: onion, vanilla and clove oil.

Question 18.
What happens when a metal piece is dropped in an acid?
Answer:
If you drop a metal piece in an acid it reacts with acid and releases hydrogen gas.

Question 19.
How can you test hydrogen gas?
Answer:
Hydrogen gas make the flair e to put off with a pop sound.So we can test it by introduc¬ing a incense stick into the mouth of the container having gas.

Question 20.
Why does balloon fill with hydrogen gas fly?
Answer:
Hydrogen gas has less weight than air. So balloon fill with hydrogen gas flies high.

Question 21.
How can you test carbon dioxide gas?
Answer:
Carbon dioxide gas put off the fire. So we can test it by introducing a lighting match stick into the mouth of the container having gas.

Question 22.
What is neutralization reaction?
Answer:
Reaction of an acid and a base is called neutralization reaction.

Question 23.
What are the substances formed in neutralization reaction?
Answer:
The substances formed in neutralization reaction are water and salt.

Question 24.
What do antacids contain?
Answer:
Antacids contain bases, eg: aluminum hydroxide, milk of magnesia.

Question 25.
Why do we get pain and itching, when an ant bites us?
Answer:
When an ant bites us, it injects formic acid into our skin. It causes pain and itching.

Question 26.
What is Acid rain?
Answer:
Rain water with slight acidic nature is called Acid rain.

Question 27.
All alkalis are bases but all bases are not alkalis. Give one example in support of this statement.
Answer:
Zinc hydroxide is a base but not an alkali. It doesn’t dissolve in water.

7th Class Science 2nd Lesson Nature of Substances Short Questions and Answers

Question 1.
Mention some food items containing acids and write the name of the acid present in them.
Answer:

Question 2.
What are mineral acids? Give examples.
Answer:

1. Some acids are prepared artificially from minerals which are extracted from the earth. Such acids are known as mineral acids or synthetic acids.
2. Hydrochloric acid, sulphuric acid and nitric acids are examples for mineral acids.

Question 3.
Mention any four daily life situations where acids are being used.
Answer:

1. Hydrochloric acid is used for bath room cleaning.
2. Sulphuric acid is used in batteries.
3. Soda water and cool drinks contain carbonic acids.
4. Fatty acids are used in manufacturing of soaps.
5. Citric acid, tartaric acid, acetic acid etc, are used in the preparation and preserva¬tion of some foods.

Question 4.
Mention any four daily life situations where bases are being used.
Answer:

1. Bath soap is prepared using potassium hydroxide.
2. Detergent soap for washing clothes is prepared using Sodium hydroxide.
3. Aluminium hydroxide is used in the preparation of tooth paste.
4. Aluminium hydroxide and milk of magnesia are used in preparation of antacids.
5. Quick lime and Potassium hydroxide are used to treat acidic soils.

Question 5.
Is it possible to test all the acids and bases simply by tasting or touching them? Why?
Answer:

1. No, It is not possible to test all the acids and bases simply by tasting or touching them.
2. Some acids like hydrochloric acid, sulphuric acid, nitric acids and bases like so¬dium hydroxide, potassium hydroxide are very harmful and strong.
3. We cannot test them by touch or taste.
4. We should use indicators to test them.

Question 6.
How to prepare turmeric indicator?
Answer:

1. Take a table spoon of turmeric powder in a plate.
2. Add little water and make it into a paste.
3. Take a white paper and apply the paste over it on both sides and let it dry.
4. After drying, cut the paper into strips.
5. Now turmeric paper strips are ready for use as indicator.

Question 7.
Do the turmeric strip act as a indicator? How?
Answer:

1. Yes, turmeric strip act as a indicator.
2. This is because turmeric is a natural indicator.
3. The colour of turmeric strip will change into reddish brown in basic solutions.
4. It remain yellow in acidic solutions.

Question 8.
How can you identify acids and bases using hibiscus indicator?
Answer:

1. Hibiscus is a natural indicator that changes its colour in acids and bases.
2. It changes its colour from violet to pink in acids.
3. It changes its colour from violet to green in bases.
4. Thus it can be used to identify acids and bases.

Question 9.
Mention the colours of different indicators in acidic and basic mediums.
Answer:

Question 10.
Magicians bring blood out of a lemon when they cut it with a knife. How is it pos-sible?
Answer:

1. It is simply a science trick.
2. Magician prepares a knife by applying an indicator like methyl orange or hibiscus solution on it.
3. Then he cut the lemon before us.
4. Due to the reaction the lemon juice (acid) turns red and we are made to believe that blood is coming out of the lemon.

Question 11.
Who introduced pH scale? How is it used?
Answer:

1. pH scale was introduced by Sorensen.
2. Strength of acid or base solution is measured in pH scale.
3. The range of pH scale is from 0 to 14.
4. pH of acids is less than 7, pH of bases is more than 7 and pH of neutral substance is 7.
5. Strength of acids decreases from 0 to 7 and strength of bases increases from 7 to 14.

Question 12.
Classify the following in to strong acid, weak acid, strong base, weak base.
Hydrochloric acid, Acetic acid, oxalic acid, Sodium hydroxide, Sulphuric acid, Po-tassium Hydroxide, Nitric acid, Ammonium hydroxide,Citric acid.
Answer:

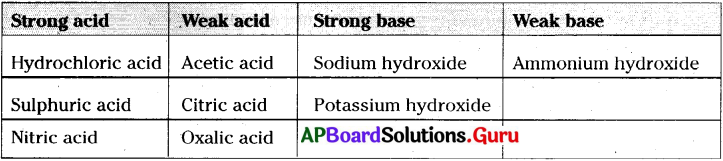
Question 13.
Pickles are not stored in aluminum or steel or copper vessels. Why?
Answer:

1. Pickles contain acids.
2. These acids react with metal containers and releases toxic substances.
3. So, we should store them in metal containers.
4. Generally, they are stored in ceramic or glass containers which do not react.

Question 14.
How can you prove carbon dioxide releases when acid reacts with calcium carbonate?
Answer:

1. Take some crushed egg shells in a test tube and pour dilute sulphuric acid until the egg shells completely sink. Egg shell is made of calcium carbonate.
2. We will observe that a gas being released.
3. Bring a lighting match stick near the mouth of test tube.
4. The gas that put off the lighting match stick indicating that the gas is carbon diox¬ide.
5. This confirms that carbon dioxide releases when acid reacts with calcium carbon¬ate.

Question 15.
What is neutralization? Give examples for neutralization reaction from day-to-day life.
Answer:

1. Neutralization is a chemical reaction where acid and base react with each other to form salt and water.
2. The bases in the antacids neutralize gastric juice and give us relief from acidity.
3. When an ant bites, it injects formic acid into the skin. It causes pain and itching. We can neutralize the acid by rubbing the paste of baking soda on the place of bite. Baking Soda is a base and it neutralizes the formic acid.
4. When soil becomes too acidic, farmers neutralize it by adding basic substances like quick lime (sunnam), potassium hydroxide etc,.
5. When soil becomes too basic they neutralize it with organic substances like com¬post which release acidic substances into the soil.

Question 16.
What is acid rain? How is it caused?
Answer:

1. Rain water with slight acidic nature is called Acid rain.
2. Air pollution is a major cause of acid rains.
3. Fuels like coal and petroleum emissions have sulphur dioxide and nitrogen dioxide etc. which react with rain water droplets and form sulphuric acid and nitric acid.
4. These acids come along with rain water to cause acid rain.

Question 17.
Bhasker said that some plants help us to find out the nature (pH)of the soil. Do you support his statement?
Answer:

1. Yes, I support his statement.
2. Hydrangea plants have different colours of flowers based on the pH of the soil.
3. If the pH of the soil is below 5.5 it gives blue flowers.
4. If the pH of the soil is below 6.5 it gives pink flowers.
5. Thus, they helps us to find the nature (pH) of soil.

Question 18.
Why do Neem/ miswak/ kanuga sticks are used as chew sticks from olden days?
Answer:

1. Neem, miswak, kanuga sticks are used as chew sticks (pandupulla) from olden days.
2. Because they have basic substances.
3. The bases in these sticks neutralizes the acids released by the bacteria in our mouth.
4. Thus they protect our oral health.

Question 19.
Write some acids and there uses in our daily life in the form of a table.
Answer:

Question 20.
Write some bases and their uses in our daily life in the form of a table.
Answer:

Question 21.
What is soap? How is it prepared?
Answer:

1. Soap is a salt with basic nature.
2. It is prepared by adding fatty acids like coconut oils to alkalis like Sodium hydroxide or Potassium hydroxide.
3. Detergent soap used to wash cloths contains Sodium hydroxide.
4. Bath soap contains Potassium hydroxide.

Question 22.
What are the precautions to be taken while handling chemicals?
Answer:

1. Do not taste and smell. Do not let it fall on the body.
2. Use a dropper while transferring acid from bottle.
3. While adding water to make dilution, pour small quantities of acid slowly into water taken in a beaker.
4. Use a holder to hold a test tube.
5. Read the precautions given on the containers of substances.

Question 23.
What precautions should be taken if the body burns due to chemicals?
Answer:

1. Start first aid immediately.
2. Remove contaminated clothes from the person.
3. Wash the affected area with plenty of water.
4. Don’t pierce the blisters.
5. Shift the person to hospital.

7th Class Science 2nd Lesson Nature of Substances Long Questions and Answers

Question 1.
Write the properties of Acids.
Answer:

1. Acids are sour to taste.
2. They turn blue litmus to red colour, methyl orange to red colour, hibiscus indicator to pink colour.
3. They don’t change the colour of phenolphthalein and turmeric indicators.
4. pH of acids is less than 7.
5. Acids react with metals and release hydrogen gas.
6. Acids react with calcium carbonate to release carbon dioxide.
7. Acids react with base to form water and salt. This reaction is called neutralisation reaction.
8. Hydrochloric acid, sulphuric acid and nitric acid are examples for acids.

Question 2.
Write the properties of Bases.
Answer:

1. Bases are bitter to taste.
2. They are slippery to touch.
3. They turn red litmus to blue colour, methyl orange to yellow colour, phenolphtha- lein to pink and hibiscus indicator to green colour.
4. They change the colour of turmeric indicator to reddish brown.
5. pH of acids is more than 7.
6. Bases like sodium hydroxide react with metals and releases hydrogen gas.
7. Bases react with acid to form water and salt. This reaction is called neutralisation reaction.
8. Sodium hydroxide, magnesium hydroxide, potassium hydroxide and calcium hy-droxide are examples for bases.

Question 3.
How can you demonstrate the neutralisation reaction in the laboratory?
Answer:
Aim: To demonstrate the neutralisation reaction.

What you need:
1) Conical flask, 2) Dropper, 3) Sodium hydroxide solution, 4) Hydro-chloric acid, 5) Phenolphthalein indicator

How to do:
Take sodium hydroxide solution in a conical flask and observe its colour. Now add 2-3 drops of phenolphthalein indicator to it. Now observe the colour. It is pink in colour. Using a dropper add dilute hydrochloric acid drop by drop to this solution, and stir gently.

What you see:
The pink colour of the solution disappears. On crystallisation water evaporates from this solution leaving the salt in the flask.

What you learn:
In this reaction acid and base reacts with each other to form salt and water. Such reactions are called neutralisation reactions.
Hydrochloric acid + sodium hydroxide → sodium chloride + water

Question 4.
Take the following solutions in to test tubes. Test them with a) red litmus, b) blue litmus, c) methyl orange and d) phenolphthalein indicators. Tabulate your results. 1)Dilute hydrochloric acid, 2) Sodium hydroxide, 3) Acetic acid, 4) Salt solution, 5) Sugar solution and 6) Soap water
Answer:

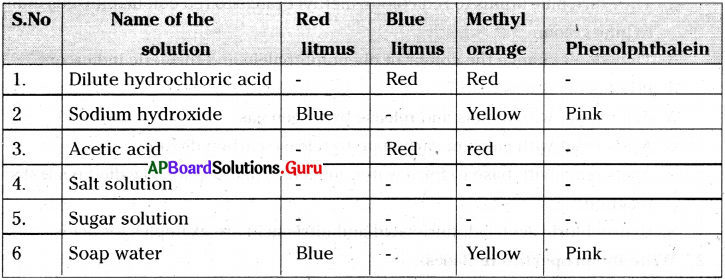
Question 5.
How can you prove that hydrogen gas releases when acid reacts with metals?
(or)
How can you produce hydrogen gas in the laboratory?
Answer:
Aim: Acid reacts with metals and produces hydrogen gas.

Materials required:
Conical flask, hydrochloric acid, zinc pieces, incense stick, match box.

Procedure:
Take 5g of zinc metal pieces in a conical flask. Pour 20 ml of dilute hydro-chloric acid into it. Now, observe what happens.

Observation:
The zinc pieces reacted with the hydrochloric acid and releases a gas. Test for hydrogen gas

Now, introduce a incense stick into mouth of the conical flask. The flame of burning stick will put off with a pop sound. This is a test for hydrogen gas. Hydrochloric acid reacts with zinc metal and forms zinc chloride, releases hydrogen gas. This reaction can be written as a word equation,
Zinc + hydrochloric acid → zinc chloride + hydrogen

Conclusion:
Hence, we can conclude that acids react with metals and release hydrogen gas.

AP Board 7th Class Science 2nd Lesson 1 Mark Bits Questions and Answers Nature of Substances

I. Multiple Choice Questions

1. Table salt contains
A) Sodium chloride
B) Sodium bicarbonate
C) Potassium chloride
D) Sodium hydroxide
Answer:
A) Sodium chloride

2. Baking soda contains
A) Sodium chloride
B) Sodium bicarbonate
C) Potassium chloride
D) Sodium hydroxide
Answer:
B) Sodium bicarbonate

3. Gastric juice means
A) Sulphuric acid
B) Citric acid
C) Antacid
D) Hydrochloric acid
Answer:
D) Hydrochloric acid

4. Sulphuric acid reacts with eggshell and releases
A) Carbondioxide
B) Hydrogen
C) Oxygen
D) None
Answer:
A) Carbondioxide

5. Substance/s formed in a neutralization reaction is/are
A) Water
B) Salt
C) A and B
D) Hydrogen
Answer:
C) A and B

6. Which of the following does not contain acid?
A) lemon
B) Bitter gourd
C) Amla
D) Tomato
Answer:
B) Bitter gourd

7. This acid is present in cool drinks
A) Sulphuric acid
B) Hydrochloric acid
C) Carbonic acid
D) Vinegar
Answer:
C) Carbonic acid

8. Bath soap is prepared using
A) Sodium hydroxide
B) Aluminum hydroxide
C) Calcium carbonate
D) Potassium hydroxide
Answer:
D) Potassium hydroxide

9. Olfactory indicator from the following
A) Hibiscus
B) Phenolphthalein
C) Clove oil
D) Methyl orange
Answer:
C) Clove oil

10. lichens are used in the preparation of
A) Litmus
B) Methyl blue
C) Phenolphthalein
D) Olfactory indicators
Answer:
A) Litmus

11. Phenolphthalein shows colour change with
A) Acids
B) Bases
C) both A & B
D) Neutral substances
Answer:
B) Bases

12. Which of the following is a strong acid?
A) Citric acid
B) Acetic acid
C) Sulphuric acid
D) Malic acid
Answer:
C) Sulphuric acid

13. This gas is lighter than air
A) Hydrogen
B) Nitrogen
C) Oxygen
D) Carbon dioxide
Answer:
A) Hydrogen

14. Product of neutralisation
A) Salt
B) Water
C) Both A & B
D) Acid
Answer:
C) Both A & B

15. Example for salt
A) Common salt
B) Antacid
C) Tooth paste
D) Clove oil
Answer:
A) Common salt

16. Acid produced in stomach
A) Sulphuric acid
B) Hydrochloric acid
C) Nitric acid
D) Carbonic acid
Answer:
B) Hydrochloric acid

17. This can be used to treat ant bite
A) Baking soda
B) Common salt
C) Vinegar
D) Turmeric
Answer:
A) Baking soda

18. pH of bases
A) 0-14
B) 7
C) more than 7
D) less than 7
Answer:
C) more than 7

19. This is responsible for acid rains
A) Sulphur dioxide
B) Nitrogen dioxide
C) Both A & B
D) Oxygen
Answer:
C) Both A & B

20. Flowers that change their colour according to the nature of soil
A) Hydrangea
B) Marigold
C) Hibiscus
D) Jasmine
Answer:
A) Hydrangea

II. Fill in the blanks.

1. Rain with slight ………….. nature is called acid rains.
2. Wash the affected burning area on skin with ………….. .
3. ………….. will be prepared by adding fatty acids to alkalis.
4. ………….. are used in making soaps.
5. ………….. are used to test the nature of substances.
6. ………….. acid is also called as Vitamin C.
7. ………….. acid is used for bath room cleaning.
8. ………….. acid is used in batteries.
9. Soda water and cool drinks contain ………….. acids.
10. Bases are ………….. to taste.
11. Bath soap is prepared using ………….. .
12. Detergent soap is prepared using
13. Bases that can dissolve in water are called ………….. .
14. The substance which is neither an acid nor a base is known as ………….. .
15. Purewater is a ………….. substance.
16. Substances which are used to test acids or bases are called ………….. .
17. Indicators obtained from natural sources are called as ………….. .
18. The most commonly used natural indicator is ………….. .
19. The colour of turmeric strip will change into ………….. in soap water.
20. Soda water turns into ………….. on adding hibiscus indicator.
21. Soap solutions turns ………….. on adding hibiscus indicator.
22. An indicator prepared from artificialsources is known as ………….. .
23. Methyl orange turns in acids and ………….. in bases.
24. Phenolphthalein turns ………….. in bases, but ………….. in acids.
25. Substances which change their smell when mixed with acid or base are known as ………….. .
26. ………….. is a mixture of different indicators and shows different colours in different solutions.
27. ………….. can show the strength of acid or alkaline substance.
28. Strength of acid or base solution is measured in ………….. scale.
29. pH of acids is ………….. .
30. pH of bases is ………….. .
31. pH of neutral substance is ………….. .
32. Natural acids are ………….. acids.
33. Acids react with metals and release gas.
34. Acids react with ………….. and release carbon dioxide gas.
35. Reaction of an acid and a base is called ………….. reaction.
36. The substances formed in neutralization reaction are ………….. and ………….. .
37. Antacids contain ………….. .
38. When an ant bites, it injects acid into the skin.
39. When soil becomes too acidic, farmers treat it by adding
40. When soil becomes too basic,farmers treat it with
41. Rain water with slight acidic nature is called
42. ………….. acid is used in the preservation of pickles and other food substances.
43. ………….. acid is used in the production of ink and leather.
44. Base used in windows cleaner is ………….. .
45. Magnesium hydroxide is used in ………….. and ………….. .
Answer:

1. acidic
2. plenty of water
3. Soap
4. Bases
5. Indicators
6. Ascorbic
7. Hydrochloric
8. Sulphuric
9. carbonic
10. bitter
11. potassium hydroxide
12. Sodium hydroxide
13. alkalis
14. neutral substance
15. Neutral
16. acid base indicators
17. Natural indicators.
18. litmus
19. reddish brown
20. pink
21. green
22. Synthetic indicator.
23. red, yellow
24. pink, does not change
25. olfactoryin dicators.
26. Universal indicatoris
27.  Universal indicator
28. pH
29. less than 7
30. more than 7
31. 7
32. weak
33. hydrogengas.
34. calcium carbonate
35. neutralization reaction.
36. water, salt
37. bases.
38. formic
39. quick lime/ potassium hydroxide.
40. compost.
41. Acid rain.
42. Acetic
43. Tannic
44. Ammonium hydroxide
45. antacid and laxative

III. Match the following

1.

Answer:

2.

Answer:

3.

Answer:

Do You Know?

Arrhenius
→ Svante Arrhenius Sweadish physical chemist gave the most modern definition of acids and alkalis. He got Noble prize in 1903 for his contribution in chemistry.

BLOOD IN LEMON…!
→ You might have seen the trick by magicians … blood coming out from a lemon when cut with a knife. This is made possible by applying an indicator like Methyl orange or hibiscus flower solution on the knife before cutting the lemon. The indicator reacts with lemon juice to give out red coloured juice. Next time you see such a trick reveal the secret.

→ Hydrangea plants have different colours of flowers based on the pH of the soil. If the pH of the soil is below 5.5 it gives blue flowers. If the pH of the soil is below 6.5 it gives pink flowers. This may helps us to find the nature of soil.

→ Neem, miswak, kanuga sticks are used as chew sticks (pandu pulla) from olden days.
Do you know why? Because they have basic substances. The bases in these sticks neutralizes the acids released by the bacteria in our mouth.

→ Soap is a salt with basic nature. It is prepared by adding fatty acids like cocohut oils to alkalis like Sodium hydroxide or Potassium hydroxide. Detergent soap is used to wash cloths contains Sodium hydroxide where as bath soap contains Potassium hydroxide. Zinc hydroxide is a. base but not an alkali. This is used in cosmetic products. All alkalis are bases but all bases are not alkalis. Discuss with your friends.

These AP 7th Class Science Important Questions 1st Lesson Food for Health will help students prepare well for the exams.

AP Board 7th Class Science 1st Lesson Important Questions and Answers Food for Health

Question 1.
What is the objective of providing mid-day meals to the school children?
Answers:
The main objective of providing a mid-day meal is to provide nutritious food to the growing children.

Question 2.
Name the food items that are served in a mid-day meal?
Answer:
Rice, Tomato dal, boiled egg, chickpea, sambar, sweet Pongal, etc.

Question 3.
What are macro nutrients?
Answer:
Nutrients that are required in large quantities to our body are called “macro nutrients”. Carbohydrates, proteins and fats are the macronutrients.

Question 4.
Why do minerals and vitamins are called micro nutrients?
Answer:
Minerals and vitamins are required in very less quantities to our body. Hence they are called “micro nutrients”.

Question 5.
Why do sports persons take glucose?
Answer:
Glucose is a type of carbohydrate that gives instant energy. For this instant energy, sports persons take glucose.

Question 6.
Give some examples for Carbohydrate rich food items.
Answer:
Rice, jowar, finger millet, maize and potato are some examples for carbohydrate rich food items.

Question 7.
In what form does the carbohydrates present in our foods?
Answer:
Carbohydrates are usually present m the form of starch and sugars in the food.

Question 8.
What is the importance of carbohydrates in our diet?
Answer:
Carbohydrates are important in our diet as they are main source of energy for the body. They are called energy giving rut rients.

Question 9.
What chemical is used to test the presence of starch?
Answer:
Iodine is used to test the presence of starch.

Question 10.
Which test will you suggest to confirm the presence of sugars?
Answer:
I will suggest “Benedict’s reagent test” to confirm the presence of sugars.

Question 11.
Sravya was lean, So the doctor suggested her to take milk, egg and pulses everyday. Can you guess why he did suggest so? Which components do they contain?
Answer:
Doctor suggested so because Sravya was lean and suffering from Protein deficiency. Milk, egg and pulses contain proteins.

Question 12.
What are body building nutrients? Why they are called so?
Answer:
Proteins are called body building nutrients. Because they are required for the formation of muscles and other body organs.

Question 13.
Give some examples for protein rich foods.
Answer:
Meat, fish, eggs, milk, pulses, soya beans etc. are some of the protein rich foods.

Question 14.
Mention some traditional food items that are rich in proteins.
Answer:
Our traditional food items like pesarattlu, minapattlu, gaarelu, vada, punugulu, sunnundalu, idly etc., are rich in proteins.

Question 15.
Does all the food items contain carbohydrates? How can we confirm this?
Answer:
No. All the food items doesn’t contain carbohydrates. We can confirm this by conducting Iodine test.

Question 16.
What are organic foods?
Answer:
The food items made of fruits and vegetables grown under organic farming are called Organic foods.

Question 17.
Which components of food are called protective food. Why?
Answer:
Minerals and vitamins are called protective nutrients because they protect our body and give good health.

Question 18.
What may happen if sea-foods and iodized salt are not included m our diet?
Answer:
If sea-foods and iodized salt are not included in our diet, it may lead to Iodine deficiency and goitre disease.

Question 19.
What measures are taken by the government to prevent anaemia among the chil-dren studying in class I – XII? ‘
Answer:
Weekly Iron Folic Acid Supplementation (WIFS) Scheme was launched in 2012 to pre-vent anaemia. Under this programme iron tablets (pink/ blue tablets) are given to children studying in class I – XII.

Question 20.
What food should be taken to prevent night blindness?
Answer:
Vitamin – A rich food such as carrot, moringa, milk products, liver oils etc, should be taken to prevent night blindness.

Question 21.
What happens due to deficiency of Vitamin K?
Answer:
Deficiency of Vitamin K leads to delay in clotting of blood.

Question 22.
What food materials will you suggest to a person suffering from scurvy?
Answer:
I will suggest to eat Vitamin C rich foods such as citrus fruits, papaya, moringa, sprouts.

Question 23.
Parveen thought that only sour fruits contain Vitamin C. Is it true?
Answer:
No, its not true. Sour fruits are rich in vitamin C but they are not the only source. Certain non-sour food materials such as papaya,moringa, sprouts are also contained vitamin C.

Question 24.
Ranga observed some fine strands or thread like structures in the boiled sweet potato. What are those? What is their importance in our digestive tract?
Answer:
Those are dietary fibres also known as roughage. They help in free bowel movement in the digestive tract and prevents constipation.

Question 25.
Give examples of food items that have dietary fibers.
Answer:
Vegetables, leafy vegetables, tubers, fruits, sprouts are the main sources of roughage. Some food materials like orange, sweet potato are rich in fibres.

Question 26.
Mention the sources of roughage.
Answer:
Vegetables/leafy vegetables, tubers, fruits, sprouts are the main sources of roughage. Some food materials like orange, sweet potato are also rich in dietary fibres.

Question 27.
Give some examples for fat rich food items.
Answer:
Butter, Ghee, Almond oil, Cooking oil.

Question 27.
Do you think drinking water is the only way to provide water to our body?
Answer:
No, many food items like milk, fruits, vegetables etc. are rich in water. They also provide water to our body.

Question 28.
What happens if we take a diet that lacks some nutrients?
Answer:
If we take a diet that lacks some nutrients, it leads to deficiency diseases.

Question 29.
What is balanced diet?
Answer:
A diet that contains all the nutrients in required quantity is called balanced diet.

Question 30.
Expand NIN.
Answer:
National Institute of Nutrition.

Question 31.
According to the ‘My plate of the day’ by NIN, which food materials should we take in large quantity?
Answer:
Vegetables should be taken in large quantity according to the ‘My plate of the day’ by NIN.

Question 32.
According to the ‘My plate of the day’ by NIN, which food materials should we take in less quantity?
Answer:
Oils arid fats Should be taken in less quantity according to the ‘My plate of the day’ by NIN.

Question 33.
What are deficiency diseases?
Answer:
Diseases caused by deficiency of certain nutrients are called deficiency diseases.

Question 34.
What happens if the proteins are inadequate in children’s diet for a long time?
Answer:
If the proteins are inadequate in children’s diet for a long time it causes a disease called Kwashiorkor.

Question 35.
What happens if the proteins and carbohydrates are not taken adequately for a long time?
Answer:
If the proteins and carbohydrates are not taken adequately for a long time it causes Marasmus disease.

Question 36.
What happens if we take food containing too much fats daily?
Answer:
If we take food containing too much fats daily, it leads to obesity. Obesity causes many health problems.

Question 37.
What is organic farming?
Answer:
The method of farming using biofertilizers and biopesticides to keep the soil alive is called Organic farming.

7th Class Science 1st Lesson Food for Health Short Questions and Answers

Question 1.
Why different food items are being served in Mid-day meal? Is it only for taste?
Answer:

1. Every food item is made up of one or more ingredients.
2. Every ingredient has one or more nutrients / components.
3. These nutrients give us energy, keep us healthy and helps in the growth and repair of our body
4. So, different food items are being served in Mid-day meal. It is not only for taste.

Question 2.
Do you know about the nutrients present in chikki? Is it same as the nutrients present in egg? Discuss.
Answer:

1. Chikki consisting of carbohydrates (Sugars), dietary fibres, vitamins and minerals.
2. It is not same as the nutrients present in egg.
3. Egg consisting of proteins and fats along with Vitamins and minerals.

Question 3.
What are the nutritive components of our food? How are they classified?
Answer:

1. Carbohydrates, Proteins, Fats, Minerals and Vitamins are the nutritive components of our food.
2. They are classified into macro and micro nutrients basing on the quantities they required to our body.
3. Carbohydrates, proteins and fats are required in large quantities. Hence, they are called ‘Macro nutrients’.
4. Minerals and vitamins are required in very less quantity. So, they are called ‘Micro-nutrients’.

Question 4.
Why do our body required proteins?
Answer:

1. Proteins are required for the formation of muscles and other body organs.
2. They regulate biochemical reactions in the body.
3. Proteins repair and heal the wounds on the body.
4. They help to build the immunity against diseases.

Question 5.
Why do elders suggest us to take green leafy vegetables regularly?
Answer:

1. Green leafy vegetables are rich source of vitamins and minerals.
2. Vitamins and minerals are protective nutrients that protect our body and give good health.
3. They also have dietary fibres which prevents constipation.
4. To be healthy green leafy vegetables should be included in our food. So elders suggest us to take green leafy vegetables regularly.

Question 6.
What are the reasons for anaemia? How can it be prevented?
Answer:

1. Anaemia is caused due to the deficiency of Iron.
2. It can be prevented by including iron-rich food materials such as meat, dry fruits, green leafy vegetables etc. in our food.

Question 7.
Why do some students get vision problems? How can it be prevented?
Answer:

1. One of the reasons for vision problems in students is Vitamin-A deficiency.
2. Vitamin-A helps in the health of the eye, hair and skin.
3. Its deficiency may lead to vision problems such as dry eyes, night blindness, cornea failure.
4. This can be prevented by including vitamin-A rich foods such as carrot, moringa, milk products, liver oils etc. in our food.

Question 8.
What are vitamins? How they ewe classified?
Answer:

1. Vitamins are micronutrients that protect our body and give good health.
2. They are of two basic types
   i) Fat soluble vitamins: A, D, E, K.
   ii) Water soluble vitamins: C, B complex

Question 9.
Why are infants exposed to mild sunlight for a short time in the morning?
Answer:

1. Exposure to the mild sunlight for a short time in the morning helps in the formation of vitamin D in the body.
2. Vitamin D helps to maintain the health of bone and teeth.
3. In infants it not only helps in formation of healthy bones and teeth but also prevents a disease called rickets.
4. So in order to provide vitamin D to infants, they are exposed to mild sunlight for a short time in the morning.

Question 10.
How can we estimate the quantity of Vitamin C m different fruits?
Answer:

1. Take the equal size slices of different fruits.
2. Keep each slice on a separate Iodine paper.
3. The fruit which made the iodine paper more discoloured contains more vitamin C,

Question 11.
Why it was advised to take Vitamin C in €owid-19 period. Discuss.
Answer:

1. During the period of Covid-I9, our immune system play key rote in cope up with the situation.
2. It fight with the coronavirus and protect us.
3. Vitamin C helps to improve our immune system.
4. As vitamin C is a immune booster, it was advised to take it in Covid -19 period.

Question 12.
Is it good to eat fruits and vegetables along with their peels? Discuss.
Answer:

1. Yes, in most of the cases it is good to eat fruits and vegetables along with their peel.
2. Because peels of fruits and vegetables contain dietary fibres.
3. They prevents constipation and keeps our digestive track healthy.
4. But we should wash fruits and vegetables thoroughly with clean water before consuming.

Question 13.
How do the infants grow by taking only milk for few months?
Answer:

1. Mother milk contains all nutrients necessary for the baby’s healthy physical development.
2. It contains carbohydrates, fats and proteins, minerals, water and vitamins in their right proportions. So it is called whole food.
3. Breast milk also contains factors that are important for protecting the infant against infection and inflammation, and contributing to healthy development of the immune system.
4. Thus mothers’ milk is naturally adapted to meet your baby’s needs so they can grow by taking only milk for few months.

Question 14.
Rupa said that boiled tap water is better than packaged / bottled water. Do you support this statement? Why/ why not?
Answer:
I support this statement because.

1. Bottled water is nothing but filtered water using reverse osmosis. This not only removes microbes but also all the minerals required for our body from water. If the tap water is boiled and filtered normally harmful microbes will be killed and removed but required minerals will not be removed. So it is better to drink boiled water than bottled water.
2. Further the empty water bottle and packets also causes pollution to our environment.

Question 15.
What is constipation? What are the causes for this? How can be it prevented?
Answer:

1. Constipation refers to bowel movements that are irregular.
2. It is a very common gastrointestinal disorder experienced by most people at some time during their life.
3. Constipation may be just due to a poor diet with insufficient fibre, poor fluid intake or a side effect of certain medication.
4. It can be prevented by taking fibre rich food and required amount of water.

Question 16.
Who proposed and recommended ‘My plate for the day’? What is its purpose?
Answer:

1. My plate for the day, is a diet plan showing the required quantities of food needed by our body.
2. This is recommended by National Institute of Nutrition (NIN) Hyderabad to promote health, prevent hidden hunger and protect us from diseases.

Question 17.
Some of our traditional foods are healthy. Support this statement with an example.
Answer:

1. Sunnundalu, boorelu made at our house during the festive season are comes under the list of complete nutrient food.
2. Black gram (protein), jaggery (carbs, iron), ghee (fats) and pressed into dows to make sunnundalu.
3. Boiled chenadal is mixed with jaggery to make poornam. It is dipped in the mixture of black gram and rice flour and water. Now this balls of poornam are cooked in oil to make boorelu (poornalu)
4. These help children to grow well as they have all the required nutrients.

7th Class Science 1st Lesson Food for Health Long Questions and Answers

Question 1.
Write a short notes on different components of food.
Answer:

1. The major nutrients in our food are. carbohydrates, proteins, fats, vitamins and minerals.
2. Carbohydrates, proteins and fats are required in large quantities. Hence, they are called Macronutrients.
3. Minerals and Vitamins are required in very less quantity. So, they are called Micro-nutrients.
4. Carbohydrates and fats mainly provide energy to our body.
5. Proteins are needed for the growth and maintenance of our body.
6. Minerals and Vitamins help in protecting our body against diseases.
7. Food also contains dietary fibres and water.
8. We may face some digestion problems like constipation due to inadequate fibres and water in the food.

Question 2.
Study the given table and answer the following questions.

1. Which minerals are required to maintain strong bones and teeth?
2. How is iron useful to our body?
3. Why should we take iodized salt?
4. Mention the source of sodium and its importance.
Answer:

1. Calcium and Phosphorus are required to maintain strong bones and teeth.
2. Iron is useful for blood production and transfer of oxygen in our body
3. We should take iodized salt to prevent iodine deficiency and Goitre disease.
4. Common salt is the major source of sodium. Sodium helps to retain water needed in our body.

Question 3.
How can you confirm the presence of vitamin C in lemon?
Answer:
Aim: To confirm the presence of vitamin C in lemon.

What you need:
1) Lemon, 2) Iodine solution, 3) Piece of white paper, 4) Knife, 5) Dropper.

How to do:
Slice a citrus fruit. Place two or three drops of iodine solution on a piece of paper.

Keep the cut side of the slice on the paper. Leave it for 15 minutes and observe. If vitamin C is present, the portion of the paper under the slice will get discoloured.

What you see :
The colour of paper under the lemon slice (discoloured)

What you learn :
Vitamin C is in lemon. (present)

Question 4.
Study the given table and answer the following questions.

1. What are the deficiency diseases caused due to deficiency of B complex vita mins?
2. Which vitamin is needed for the health of the nerves and blood cells?
3. What food materials will you suggest to a person suffering Tom scurvy?
4. Mention the deficiency diseases of vitamin A.
Answer:

1. Beri beri, fits, pellagra, scaly skin, photophobia, loss oi memory are the deficiency diseases caused due to deficiency of B complex vitamins.
2. Vitamin E is needed for the health of the nerves and blood cells.
3. I will suggest him to eat vitamin C rich foods such as citrus fruits, papaya, moringa, sprouts etc.
4. Dry eyes, night blindness, cornea failure the deficiency diseases of vitamin A.

Question 5.
Write a short notes on disadvantages of junk food.
Answer:

1. Pizza, burgers, chips, fast foods, noodles, cool drinks etc. are junk foods.
2. They consists of more fats and no fibres.
3. They cannot he digested easily.
4. Eating junk food on a regular basis damages our digestive system.
5. Our body is being deprived of the other required nutrients.
6. It leads to an increased risk of obesity and other health issues.

Question 6.
Give reasons for the following.
A) Eating whole grains like maize, barley, ragi, bajra, wheat, etc. is healthy.
B) Removing fiber from wheat flour to make chapatis is unhealthy.
C) Drinking butter milk, lassi, sharbat, lemon water is healthy.
D) Eating white bread, buns and noodles daily is unhealthy.
E) Drinking tea/coffee immediately before or after eating food is unhealthy.
F) Consuming jaggery and chikki is healthy.
G) Eating sprouts is healthy.
H) Eating street food like samosa, chaat on regular basis is unhealthy.
I) Checking date of manufacture, date of expiry, MRP, etc.,while buying packaged food is healthy.
J) Eating fruits without washing them is unhealthy.
Answer:
A) Whole grains are nutritious and available locally. Grains like bajra and ragi are rich in calcium and iron. Unlike these, refined flour has very little to no nutrients and less fiber.

B) Fiber is important for digestive health and regular bowel movements. It is required for a healthy gut.

C) These locally available drinks are healthy and nutritious. Packaged cold drinks are high in sugar and do not have any nutrients. They also contain high amounts of acid, which is bad fpr the teeth and bones.

D) These are made of refined flour and hence have no micronutrients and fiber. Therefore,consumption of these in too much quantity regularly is not good for health.

E) One should not drink tea coffee before and after eating food at least for one hour as it impairs the absorption of iron in the body.

F) Jaggery and chikki are easily available locally. Jaggery is a good source %of iron. Chikki is rich in Vitamin A, protein, iron and calcium.

G) Sprouted grains and pulses have plenty of micronutrients and are a good source of energy and proteins. Taking sprouts daily will be good to meet the growth require-ments of children.

H) Street food like samosa, chowmein, momos, chaat, etc. could be prepared in the open and so are exposed to dirt, dust and insects and carry the risk of infections. Also this food is low in fiber, high in fat and sugar. Eating too much of it, an give rise to obesity and other diseases like diabetes.

I) No food item should be consumed after the expiry date as it is not fit for consump-tion. One should not pay more than the MRP. So it is essential to check these details.

J) Fruits and vegetables may contain bacteria and pesticides, therefore, should be washed before consumption. It is equally important to wipe all packages, tins, bottles before storing and consuming.

Question 7.
Healthy eating habits play a vital role in maintaining proper health. Certain eating habits are given in the following table, mention whether they are healthy or unhealthy.
Answer:

Question 8.
Write about the 7 C’s prescribed by FSSAI to prevent foods contamination.
Answer:
Food hygiene is as important as healthy eating habits. To prevent foods contamination FSSAI prescribed seven food hygiene practices in the form of 7C’s. There are

1. Check : Select food that is fresh.
2. Clean : Wash and wipe all containers before storing food.
3. Cover : Keep all food and drinking water covered in the storage area.
4. Cross contamination avoided : Keep raw and cooked food apart.
5. Cook : Cook food thoroughly and ensure it is freshly cooked.
6. Cool/ Chill : Refrigerate or freeze meat, poultry, eggs and other perishables.
7. Consume : Serve food in a clean environment and use clean utensils.

AP Board 7th Class Science 1st Lesson 1 Mark Bits Questions and Answers Food for Health

I. Multiple Choice Questions

1. Which of the following is good for health?
A) Sprouts
B) Packaged cool drinks
C) Junk foods
D) Above all
Answer:
A) Sprouts

2. Chikki (Chickpea) contains
A) Proteins
B) Iron
C) Calcium
D) Above all
Answer:
D) Above all

3. Street food have
A) rich in fibre
B) rich in fat
C) rich in minerals
D) above all
Answer:
B) rich in fat

4. Which water is better to drink?
A) Packaged drinking water
B) Tap water
C) Boiled water
D) Above all
Answer:
C) Boiled water

5. Ascorbic acid is called as
A) Vitamin A
B) Vitamin C
C) Vitamin K
D) Vitamin E
Answer:
B) Vitamin C

6. This gives instant energy to the body.
A) Chicken
B) Egg
C) Glucose
D) Ghee
Answer:
C) Glucose

7. Which of the following is the main source of energy for our body?
A) carbohydrates
B) proteins
C) fats
D) vitamins
Answer:
A) carbohydrates

8. Identify the energy giving food.
A) carbohydrates
B) proteins
C) fats
D) A & C
Answer:
D) A & C

9. Identify the food item rich in carbohydrates.
A) Pulses
B) Groundnut
C) Potato
D) Almond
Answer:
C) Potato

10. Reagent used to test the presence of starch
A) Benedict’s reagent
B) Iodine
C) Copper sulphate solution
D) All the above
Answer:
B) Iodine

11. Starch turn in to this colour when it come in contact with iodine solution
A) Blue black
B) Violet
C) Pink
D) Reddish green
Answer:
A) Blue black

12. Which of the following food sample gives blue black colour with iodine solution?
A) Jowar
B) Rice
C) Maize
D) All the above
Answer:
D) All the above

13. Reagent used to test the presence of sugar
A) Benedict’s reagent
B) Iodine
C) Copper sulphate solution
D) Sodium hydroxide solution
Answer:
A) Benedict’s reagent

14. Which of the following are called body building nutrients?
A) carbohydrates
B) proteins
C) fats
D) A & C
Answer:
B) proteins

15. Identify the functions of proteins from the following.
A) Helps in the formation of muscles and other body organs.
B) Regulate biochemical reactions in the body.
C) Repair and heal the wounds on the body.
D) All the above
Answer:
D) All the above

16. Find the odd one out.
A) Meet
B) Maize
C) Egg
D) Soya been
Answer:
B) Maize

17. Animal source of protein ….
A) Milk
B) Fish
C) Pulses
D) A & B
Answer:
D) A & B

18. What colour change will you observe when egg white reacts with 2% copper sulphate and 10% sodium hydroxide solutions
A) White to blue black
B) White to violet
C) White to pink
D) White to reddish green
Answer:
B) White to violet

19. Which of the following gives more energy when they are taken in equal quantities?
A) carbohydrates
B) proteins
C) fats
D) vitamins
Answer:
C) fats

20. Groundnuts paste turns white paper in to
A) Transparent
B) Translucent
C) Opaque
D) Violet colour
Answer:
B) Translucent

21. What tablets will you suggest to an anaemia patient?
A) Calcium
B) Iron
C) Vitamin D
D) Phosphorus
Answer:
B) Iron

22. Minerals and vitamins are called
A) Energy giving nutrients
B) Body building nutrients
C) Protective nutrients
D) Anutritive components
Answer:
C) Protective nutrients

23. Mineral element responsible for strong bones and teeth
A) Calcium
B) Iron
C) Phosphorus
D) A & C
Answer:
D) A & C

24. Mineral element responsible for blood production and transfer of oxygen
A) Calcium
B) Iron
C) Phosphorus
D) Sodium
Answer:
B) Iron

25. Deficiency of this mineral causes Goitre disease.
A) Calcium
B) Iron
C) Iodine
D) Sodium
Answer:
C) Iodine

26. Milk, curd are rich in
A) Calcium
B) Iron
C) Iodine
D) Sodium
Answer:
A) Calcium

27. This mineral helps in retaining the water needed for our body.
A) Calcium
B) Iron
C) Phosphorus
D) Sodium
Answer:
D) Sodium

28. Common salt is the major source for
A) Calcium
B) Sodium
C) Phosphorus
D) Iron
Answer:
B) Sodium

29. Iodized salt helps in preventing
A) Anaemia
B) Goitre
C) Night blindness
D) Scurvy
Answer:
B) Goitre

30. Which of the following is not a fat-soluble vitamin?
A) Vitamin – A
B) Vitamin – B
C) Vitamin – D
D) Vitamin – E
Answer:
B) Vitamin – B

31. Which of the following is a water-soluble vitamin?
A) Vitamin – A
B) Vitamin – K
C) Vitamin – E
D) Vitamin – C
Answer:
D) Vitamin – C

32. Deficiency of vitamin – A causes
A) Dry Eyes
B) Night blindness
C) Cornea failure
D) All the above
Answer:
D) All the above

33. Which of the following is not a deficiency disease of vitamin – B complex?
A) Beri-Beri
B) Scurvy
C) Fits
D) Pellagra
Answer:
B) Scurvy

34. Deficiency of vitamin – D causes
A) Rickets
B) Scurvy
C) Night blindness
D) Fertility disorders
Answer:
A) Rickets

35. Scurvy caused due to the deficiency of
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
C) Vitamin – C

36. Fertility disorders may be due to the deficiency of
A) Vitamin – A
B) Vitamin – B
C) Vitamin – D
D) Vitamin – E
Answer:
D) Vitamin – E

37. Somu is suffering from delay in blood clotting during injuries. What might be the reason?
A) Vitamin – A deficiency
B) Vitamin – K deficiency
C) Vitamin – D deficiency
D) Vitamin – E deficiency
Answer:
B) Vitamin – K deficiency

38. This vitamin is responsible for health of the bone and teeth.
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
D) Vitamin – D

39. Function of vitamin A
A) Health of Nerves
B) Formation of RBC
C) Health of Bone and teeth
D) Health of eye, hair and skin
Answer:
D) Health of eye, hair and skin

40. This vitamin is responsible for health of gums.
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
C) Vitamin – C

41. Vitamin – E is responsible for
A) Health of Nerves
B) Formation of RBC
C) Health of Bone and teeth
D) Health of eye, hair and skin
Answer:
A) Health of Nerves

42. Citrus fruits are the rich source of this vitamin.
A) Vitamin – C
B) Vitamin – B
C) Vitamin – A
D) Vitamin – K
Answer:
A) Vitamin – C

43. Sunlight is required to form this vitamin in our body.
A) Vitamin – A
B) Vitamin – B
C) Vitamin – D
D) Vitamin – E
Answer:
C) Vitamin – D

44. Eating carrots can prevent
A) Rickets
B) Scurvy
C) Night blindness
D) Fertility disorders
Answer:
C) Night blindness

45. This vitamin play an important role in increasing immunity.
A) Vitamin – A
B) Vitamin – C
C) Vitamin – D
D) Vitamin – K
Answer:
B) Vitamin – C

46. Which vitamin discolourises the iodine paper?
A) Vitamin – A
B) Vitamin – B
C) Vitamin – C
D) Vitamin – D
Answer:
C) Vitamin – C

47. Dietary fibres prevent
A) Rickets
B) Scurvy
C) Night blindness
D) Constipation
Answer:
D) Constipation

48. Anutritive component of our food is
A) carbohydrates
B) proteins
C) fats
D) water
Answer:
D) water

49. Weight of the water in our body is nearly
A) 2/3 of our body weight
B) 3/2 of our body weight
C) 1/5 of our body weight
D) 14 of our body weight
Answer:
A) 2/3 of our body weight

50. Function of water in our body
A) Maintains the temperature of our body
B) Helps in excretion of wastes
C) Helps in easy movement of the food in digestive track
D) All the above
Answer:
D) All the above

51. Irregular bowel movements refer to
A) Rickets
B) Constipation
C) Night blindness
D) Scurvy
Answer:
B) Constipation

52. This may be the cause for constipation
A) poor diet with insufficient fibre
B) poor fluid intake
C) side effect of certain medication blindness
D) all the above
Answer:
D) all the above

53. Food component present more in Black gram
A) carbohydrates
B) proteins
C) fats
D) all the above
Answer:
B) proteins

54. Jaggery is a rich source of
A) Calcium
B) Iron
C) Iodine
D) Sodium
Answer:
B) Iron

55. National Institute of Nutrition (NIN) is located at
A) Delhi
B) Mumbai
C) Pune
D) Hyderabad
Answer:
D) Hyderabad

56. Inadequate proteins in children’s diet for a long-time cause
A) Marasmus
B) Constipation
C) Kwashiorkor
D) Obesity
Answer:
C) Kwashiorkor

57. Inadequate carbohydrates and proteins in children’s diet for a long-time cause
A) Marasmus
B) Constipation
C) Kwashiorkor
D) Obesity
Answer:
A) Marasmus

58. Taking food containing too much fat leads to
A) Marasmus
B) Constipation
C) Kwashiorkor
D) Obesity
Answer:
D) Obesity

59. Which of the following should be taken more in our diet?
A) Cereals
B) Pulses
C) Vegetables
D) Obesity
Answer:
C) Vegetables

60. Which of the following should be taken in very less quantity in our diet?
A) Cereals
B) pulses
C) Vegetables
D) Oils
Answer:
D) Oils

61. How much quantity of milk /curd should be taken every day?
A) 300 ml
B) 100 ml
C) 500 ml
D) 1000 ml
Answer:
A) 300 ml

62. Grains like bajra and ragi are rich in
A) Calcium
B) iron
C) Both A&B
D) Calcium
Answer:
C) Both A&B

63. Which of the following is not a C from the 7 C’s prescribed by FSSAI?
A) Check
B) Clean
C) Control
D) Cover
Answer:
C) Control

II. Fill in the blanks.

1. Eating junk food on a regular basis damages our ………….. system.
2. Grains like bajra and ragi are rich in ………….. and ………….. .
3. Packaged cold drinks contain high amounts of ………….., which is bad for the teeth and bones.
4. Drinking of tea/ coffee less than one hour before and after eating food impairs the absorption of ………….. in the body.
5. Jaggery is a good source of ………….. .
6. Carbohydrates, proteins and fats are required in ………….. quantity. Hence, they are called ………….. .
7. Minerals and Vitamins are required in very ………….. quantity. So, they are called ………….. .
8. Carbohydrates and fats mainly provide ………….. to our body.
9. Sports persons take glucose as it gives ………….. .
10. Carbohydrates are usually present in the form of ………….. and ………….. in the food.
11. Presence of starch is confirmed by doing test.
12. Starch turns into in colour when it come in contact with Iodine solution.
13. ………….. test confirms the presence of sugars.
14. ………….. are needed for the growth and maintenance of our body.
15. ………….. are called body building nutrients.
16. repair and heal the wounds on the body.
17. Proteins turn into ………….. colour when they react with 2% copper sulphate solution and 10% sodium hydroxide solution.
18. Pulses are rich in ………….. .
19. ………….. give more energy when compared to the same amount of carbohydrates.
20. Fats turn the white paper ………….. .
21. ………….. and ………….. help in protecting our body against diseases.
22. ………….. and ………….. are required for strong bones and teeth.
23. ………….. is the mineral responsible for blood production and transfer of oxygen.
24. ………….. is the mineral required for the thyroid hormone secretions.
25. Sea foods are rich source of ………….. .
26. ………….. is the mineral that helps to retain water needed for the body.
27. Weekly Iron Folic Acid Supplementation Scheme was launched to prevent
28. Vitamins – A, D, E, K are ………….. soluble Vitamins.
29. Vitamins – C, B complex are ………….. soluble Vitamins.
30. Health of eye, hair and skin is maintained by the vitamin ………….. .
31. Dry eyes is caused due to the deficiency of the vitamin ………….. .
32. Pellagra is caused due to the deficiency of the vitamin ………….. .
33. Health of skin, teeth, gums and blood cells is maintained by the vitamin ………….. .
34. Eating Citrus fruits can prevent the diseases ………….. .
35. Sun light is required to form the vitamin in our body.
36. ………….. is the disease caused due to the deficiency of vitamin D.
37. Vitamin E is responsible for the health of ………….. .
38. Deficiency of Vitamin E causes ………….. .
39. Vitamin ………….. helps in the clotting of blood when we get wounded.
40. Vitamin ………….. plays an important role in increasing disease resistant or immunity.
41. ………….. paper gets discoloured with vitamin C.
42. The substances which made the iodine paper more discoloured contains more vitamin ………….. .
43. ………….. help in free bowel movement in the digestive tract and prevent the constipation.
44. Water constitutes nearly ………….. of our body weight.
45. ………….. refers to bowel movements that are irregular.
46. A diet that contains all the nutrients in required quantity is called ………….. .
47. NIN is located at ………….. .
48. According to ‘My plate for the day’ by NIN quantity of nuts and seeds recommended is ………….. .
49. Diseases caused by deficiency of certain nutrients are called ………….. .
50. Healthy eating habits and also play a key role in maintaining of health.
51. If the proteins are inadequate in children’s diet for a long time it causes ………….. .
52. If the proteins and carbohydrates are not taken adequately for a long time it causes ………….. .
53. If we take food containing too much fats daily, it leads to ………….. .
Answer:

1. digestive
2. Calcium and iron
3. acid
4. iron
5. iron
6. More, Macro nutrients
7. Less micro nutrients
8. energy
9. instant energy
10. Starch and sugars
11. iodine
12. black blue
13. Benedict’s reagent
14. Proteins
15. Proteins
16. Proteins
17. violet
18. Proteins
19. fat
20. translucent
21. Minerals and Vitamins
22. Calcium and Phosphate
23. Iron
24. Iodine
25. Iodine
26. Sodium
27. Anemia
28. Fat
29. water
30. A
31. A
32. B
33. C
34. scurvy
35. D
36. rickets
37. nerves and blood cells
38. Fertility disorders
39. K
40. C
41. iodine
42. C
43. Dietary fibres / roughage
44. 2/3
45. Constipation
46. balanced diet
47. Hyderabad
48. 30 gms/day
49. Deficiency diseases
50. hygiene
51. Kwashiorkor
52. Marasmus
53. obesity

III. Match the following

1.

Answer:

2.

Answer:

3.

Answer:

4.

Answer:

Do You Know?

→ Weekly Iron Folic Acid Supplementation (W1FS) Scheme was launched in 2012 to prevent anaemia. Under this programme iron tablets (pink/ blue tablets) are given to children studying in classes I-XII. This service is delivered through school teachers. These tablets should be consumed after the main meal of the day otherwise side effects such as nausea may occur. Folic acid is a supplement and needs a food to mix with before entering the blood stream.

CONSTIPATION
→ It is a disorder condition resembling Vibandha described in Ayurveda. It refers to bowel movements that are irregular. It is a very common gastro-intestinal disorder experienced by most people at some time during their life. Constipation may be just due to a poor diet with insufficient fibre, poor fluid intake or a side effect of certain medication.

HEALTH AND HAPPINESS WITH TRADITIONAL FOODS
→ Sunnundalu, boorelu made at our house during the festive season are comes under the list of complete nutrient food. Have you seen the ingredients that your mother uses to make sunnundalu? Add black gram (protein), jaggery (carbs, iron), ghee(fats) and pressed into dough to make sunnundalu. Boiled chenadal is mixed with jaggery to make poornam. It is dipped in the mixture of black gram and rice flour and water.Now this balls of poornam are cooked in oil to make boorelu (poornalu). These help children to grow well. That is why these must be cooked and shared with everyone. Most of the eateries available at Sweet Stalls are not just whole foods, they are not just real nutrients. So eat homemade janthikalu, garelu, sunnundalu, laddus well.

→ Pizza, burgers, chips, fast foods, noodles, cool drinks etc., are junk foods. They consists of more fats and no fibres. They cannot be digested easily. Eating junk food on a regular basis damages our digestive system.Our body is being deprived of the other required nutrients. It leads to an increased risk of obesity and other health issues.

ORGANIC FOODS
→ The method of farming using biofertilizers and biopesticides to keep the soil alive is called Organic farming. The food items made of fruits and vegetables grov under organic farming are called Organic foods. These are good for health. Now a days farmers and people are showing interest on organic farming and organic food items.

These AP 8th Class Physical Science Important Questions 11th Lesson కొన్ని సహజ దృగ్విషయాలు will help students prepare well for the exams.

AP Board 8th Class Physical Science 11th Lesson Important Questions and Answers కొన్ని సహజ దృగ్విషయాలు

8th Class Physics 11th Lesson కొన్ని సహజ దృగ్విషయాలు 1 Mark Important Questions and Answers

ప్రశ్న 1.
భూకంపం ద్వారా విడుదలయ్యే విధ్వంస శక్తిని దేనితో కొలుస్తారు?
జవాబు:
భూకంపం ద్వారా విడుదలయ్యే విధ్వంస శక్తిని “భూకంప లేఖిని” లేదా “భ్రామక పరిమాణ స్కేలు’ ద్వారా కొలుస్తారు.

ప్రశ్న 2.
రెండు వస్తువులు ఒకే ఆవేశం కలిగి ఉంటే ఏం జరుగుతుంది? తెల్పండి.
జవాబు:
రెండు వస్తువులు ఒకే ఆవేశం కలిగి ఉంటే వాటి మధ్య వికర్షణ బలం ఉంటుంది.

ప్రశ్న 3.
రెండు వస్తువులు వేరు వేరు ఆవేశాలు కలిగి ఉంటే ఏం జరుగుతుందో తెల్పండి?
జవాబు:
రెండు వస్తువులు వేరు వేరు ఆవేశాలు కలిగి ఉంటే వాటి మధ్య ఆకర్షణ బలం ఉంటుంది.

ప్రశ్న 4.
వస్తువుకున్న ఆవేశాన్ని గుర్తించడానికి ఏ పరికరం ఉపయోగిస్తారు?
జవాబు:
ఒక వస్తువు ఆవేశాన్ని గుర్తించడానికి విద్యుదర్శినిని ఉపయోగిస్తారు.

ప్రశ్న 5.
సహజ దృగ్విషయాలు అని వేటిని అంటారు?
జవాబు:
వరదలు, తుపాన్లు, వడగండ్ల వర్షం, మెరుపులు, ఉరుములు, భూకంపాలు, సునామీలు మరియు అగ్ని పర్వతాలు పేలడం వంటివి సంభవించే వాటిని సహజ దృగ్విషయాలు అని అంటారు.

ప్రశ్న 6.
విద్యుత్ ఆవేశ బలాల సూత్రాలను రాయండి.
జవాబు:

1. సజాతి ఆవేశాల మధ్య వికర్షణ బలాలు ఉంటాయి.
2. విజాతి ఆవేశాల మధ్య ఆకర్షణ బలాలు ఉంటాయి.

ప్రశ్న 7.
ఆవేశం గల ఒక వస్తువును ఆవేశం లేని వస్తువు దగ్గరకు తీసుకొస్తే ఆకర్షణకు గురి అవుతుంది. ఎందుకు?
జవాబు:
ఆవేశం గల ఒక వస్తువును ఆవేశం లేని వస్తువు దగ్గరకు తీసుకు వస్తే ఆవేశం లేని వస్తువుపై, వ్యరేక ఆవేశం ప్రేరేపింపబడి అది ఆకర్షణకు గురవుతుంది.

ప్రశ్న 8.
ఒక వస్తువుపై ఆవేశం ఉన్నదో లేదో గుర్తించడానికి ఏ ధర్మం సరియైనది?
జవాబు:
ఒక వస్తువుపై ఆవేశం ఉన్నదో లేదో గుర్తించడానికి వికర్షణ ధర్మం సరియైనది.

ప్రశ్న 9.
భూకంప తరంగాలు అనగానేమి?
జవాబు:
భూ అంతర్భాగంలో కదలికలు భూ ఉపరితలంపై తరంగాలను ఉత్పత్తి చేస్తాయి. ఈ తరంగాలను భూకంప తరంగాలు అంటారు.

ప్రశ్న 10.
భూకంప తరంగాలను దేని ద్వారా గుర్తిస్తారు?
జవాబు:
భూకంప తరంగాలను భూకంప లేఖిని ద్వారా గుర్తిస్తారు.

ప్రశ్న 11.
ఉత్తర భారతదేశంలో భూకంప ప్రభావిత ప్రాంతాలు ఏవి?
జవాబు:
భారతదేశంలో కాశ్మీర్, పశ్చిమ మరియు మధ్య హిమాలయాలు, ఈశాన్య ప్రాంతాలు, కచ్ తీరం. రాజస్థాన్. గంగా పరీవాహక ప్రాంతాలు అత్యంత భూకంప ప్రభావిత ప్రాంతాలు.

ప్రశ్న 12.
భూమిలో ఎన్ని పొరలు ఉంటాయి? అవి ఏవి?
జవాబు:
భూమిలో ముఖ్యంగా మూడు పొరలు ఉంటాయి. అవి :

1. భూపటలం
2. ప్రావారం
3. భూకేంద్రం.

భూకేంద్రంలో రెండు పొరలు ఉంటాయి. అవి :

1. అంతర్ భూకేంద్రం,
2. బాహ్య భూకేంద్రం

ప్రశ్న 13.
భూకంప ప్రభావిత ప్రాంతాలు అనగానేమి?
జవాబు:
భూమి లోపల గల పలకల కదలిక వల్ల కొన్ని ప్రాంతాలలో భూకంపాలు తరచుగా రావడానికి అవకాశం ఉంటుంది. భూ ఉపరితలంపై ఈ పలకలకు దరిదాపుల్లో ఉండే ఈ బలహీన ప్రాంతాలను సెస్మిక్ ప్రాంతాలు లేదా భూరు ప్రభావిత ప్రాంతాలు అంటారు.

ప్రశ్న 14.
తటిద్వాహకం అనగానేమి?
జవాబు:
పిడుగుల (మెరుపు) ల నుండి పెద్ద పెద్ద భవనాలను, కట్టడాలను రక్షించడానికి ఉపయోగించే దానిని తటిద్వాహకం అంటారు.

ప్రశ్న 15.
కాగితంతో రుద్దిన రబ్బరు బెలూనను చిన్న కాగితపు ముక్కల దగ్గరకు తీసుకువచ్చినపుడు నీవు గమనించిన కిషయాలు ఏమిటి?
జవాబు:

1. రబ్బరు బెలూన్ కాగితం ముక్కలను ఆకర్షించును.
2. రబ్బరు బెలూన్ కాగితం ముక్కలపై ప్రభావం చూపదు.

8th Class Physics 11th Lesson కొన్ని సహజ దృగ్విషయాలు 2 Marks Important Questions and Answers

ప్రశ్న 1.
ఏదైనా ఒక వస్తువును ఆవేశపరచడానికి మూడు పద్ధతులను రాయండి.
జవాబు:

1. ఒక వస్తువును మరొక వస్తువుతో రాపిడికి గురిచేయడం వలన ఆవేశపరచవచ్చును.
2. ఒక వస్తువును ఆవేశం గల వస్తువు దగ్గరకు తెచ్చినపుడు ఆ వస్తువులో ఆవేశం ప్రేరేపించడం వలన ఆవేశ పరచవచ్చును.
3. ఒక వస్తువుకు, ఆవేశ వస్తువును తాకించడం వలన ఆవేశం గల వస్తువు నుండి ఆ వస్తువులోకి ఆవేశం బదిలీ అగుట వలన ఆవేశ పరచవచ్చును.

ప్రశ్న 2.
భ్రామక పరిమాణ స్కేలు గురించి కొన్ని ఉపయోగాలు రాయండి.
జవాబు:

1. భ్రామక పరిమాణ స్కేలు భూకంప తీవ్రతను కొలుచుటకు ఉపయోగిస్తారు.
2. భూకంపాలను భ్రామక పరిమాణ స్కేలు ద్వారా కచ్చితంగా నిర్ధారించవచ్చును.
3. ఈ పద్ధతి రిక్టర్ స్కేలు పద్ధతి కంటే ఉన్నతమైనది.

ప్రశ్న 3.
భూకంపాలు ఏ విధంగా ఏర్పడతాయో తెల్పండి.
జవాబు:
భూమి ఉపరితలంలో ఒకే పొరగా లేదు. ఇది విడివిడి ముక్కలుగా ఉంటుంది. ఈ ముక్కలను పలకలు అంటారు. ఈ పలకలు నిరంతర చలనంలో ఉంటాయి. ఒక పలక మరొక పలకను ఢీకొన్నప్పుడు కాని, రెండింటి మధ్య రాపిడి జరిగినప్పుడు కాని భూ పటలంలో కదలికలు వస్తాయి.

భూ అంతర్భాగంలో జరిగే ఇటువంటి కదలికలు భూ ఉపరితలంలో భూకంపాలను ఏర్పరుస్తాయి.

ప్రశ్న 4.
ఒక వస్తువుపై ఆవేశము ఉన్నదో లేదో గుర్తించడానికి “ఆకర్షణ ధర్మం” సరైనది కాదు. ఎందుకో వివరించండి.
జవాబు:

1. ఒక తటస్థ వస్తువును, ఆవేశ వస్తువు వద్దకు తీసుకొనివస్తే ఆకర్షిస్తుంది.
2. ఒక ఆవేశ వస్తువును, దాని వ్యతిరేక ఆవేశ వస్తువు వద్దకు తీసుకొనివస్తే ఆకర్షిస్తుంది.
3. ఒక వస్తువుపై ఆవేశం ఉన్నదో లేదో తెలుసుకొనుటకు ఆవేశం గల వస్తువు దగ్గరకు తీసుకొనివస్తే ఆకర్షించినట్లైతే ఆ వస్తువుపై తటస్థ ఆవేశం లేదా వ్యతిరేక ఆవేశం మాత్రమే ఉండాలి. కాని తటస్థ ఆవేశమా, వ్యతిరేక ఆవేశమా అని కచ్చితంగా చెప్పలేము. కాబట్టి “ఆకర్షణ ధర్మం” సరియైనది కాదు.

ప్రశ్న 5.
తటిద్వా హకం (Lightning conductor) అనగానేమి? ఇది భవనాలను ఎలా రక్షిస్తుంది?
జవాబు:

1. పిడుగుల (మెరుపు)ల నుండి పెద్ద పెద్ద భవనాలను, కట్టడాలను రక్షించడానికి ఉపయోగించే దానిని తటిద్వాహకం అంటారు.
2. భవనం కన్నా కొద్దిగా ఎత్తుగా ఉండే లోహపు కడ్డీని భవన నిర్మాణ సమయంలోనే గోడలో అమర్చుతారు.
3. లోహపు కడ్డీ ఒక చివర గాలిలో ఉంటుంది. రెండవ చివరను భూమిలోకి పాతుతారు.
4. భవనం కంటే లోహపుకడ్డీ ఎత్తులో ఉంటుంది కనుక అది మేఘాలకు దగ్గరగా ఉండటం వల్ల ఇది మొదట ఆవేశాన్ని స్వీకరిస్తుంది.
5. ఇది మంచి విద్యుత్ వాహకం కనుక భవనానికి ఎటువంటి నష్టం జరగకుండా ఆవేశాన్ని భూమికి చేరవేస్తుంది.

ప్రశ్న 6.
భూకంపాలు ఏ విధంగా ఏర్పడుతాయో వివరించండి.
జవాబు:

1. భూమి ఉపరితలంలో ఒకే పొరగా లేదు. ఇది విడివిడి ముక్కలుగా ఉంటుంది.
2. ఈ ముక్కలను పలకలు అంటారు.
3. ఈ పలకలు నిరంతర చలనంలో ఉంటాయి.
4. ఒక పలక మరో పలకను ఢీకొన్నప్పుడు కాని, రెండింటి మధ్య రాపిడి జరిగినపుడు కాని భూ పటలంలో కదలికలు వస్తాయి.
5. భూ అంతర్భాగంలో జరిగే ఇటువంటి కదలికలు భూ ఉపరితలంలో భూకంపాలను ఏర్పరుస్తాయి.

ప్రశ్న 7.
భ్రామక పరిమాణ స్కేలును వివరించండి.
జవాబు:

1. భ్రామక పరిమాణ స్కేలు భూకంప తీవ్రతను కొలుచుటకు ఉపయోగిస్తారు.
2. ఇది భూ ఉపరితలం వద్ద వచ్చే విస్తాపనంతో సంబంధం లేకుండా భూ అంతర్భాగంలో గల పలకల విస్తాపనంపై ఆధారపడి పనిచేస్తుంది.
3. భూకంపాలను భ్రామక పరిమాణ స్కేలు ద్వారా కచ్చితంగా నిర్ధారించవచ్చును.
4. ఈ పద్ధతి రిక్టర్ స్కేలు పద్ధతి కంటే ఉన్నతమైనది.

ప్రశ్న 8.
భూకంప ప్రమాద పటం ప్రకారం ఆంధ్రప్రదేశ్ లోని జోన్లను వివరించండి.
జవాబు:

1. భూకంప ప్రమాద పటం ప్రకారం ఆంధ్రప్రదేశ్ లోని కొన్ని ప్రాంతాలు 2, 3 జోన్లలో ఉన్నాయి.
2. ఆంధ్రప్రదేశ్ ఆగ్నేయ ప్రాంతంలోని చిత్తూరు, వై.ఎస్.ఆర్.కడప, నెల్లూరు మరియు కృష్ణా, గోదావరి మైదాన ప్రాంతాలు 3వ జోన్లో ఉన్నాయి.
3. హైదరాబాద్ నగరం 2వ జోన్లో ఉన్నది.

8th Class Physics 11th Lesson కొన్ని సహజ దృగ్విషయాలు 4 Marks Important Questions and Answers

ప్రశ్న 1.
ఒక వస్తువు ప్రేరణ వలన ఆవేశపరచడానికి, ఆవేశం గల వాహకం ద్వారా ఆవేశపరచడానికి మధ్యగల భేదాలను రాయండి.
జవాబు:

ప్రశ్న 2.
మెరుపులు, ఉరుములు ఏ విధంగా ఏర్పడునో వివరించండి.
జవాబు:

1. గాలిలో మేఘాలు ప్రయాణించేటప్పుడు గాలిలో కణాలతో ఘర్షణ వల్ల మేఘాలు ఆవేశపూరితం అవుతాయి.
2. మేఘాల ఉపరితలాలు చాలా పెద్దవి కనుక ఈ ఉపరితలాలపై ఆవేశం చాలా ఎక్కువ మొత్తంలో నిలువ ఉంటుంది.
3. ఒక ఆవేశపూరిత మేఘం దగ్గరగా మరొక మేఘం వచ్చినపుడు అది రెండవ మేఘంపై వ్యతిరేక ఆవేశాన్ని ప్రేరేపింపజేస్తుంది.
4. ఈ మేఘాలపై గల ఆవేశం ఒక మేఘం నుండి మరొక మేఘం పైకి వెళ్ళడానికి ప్రయత్నిస్తుంది. కానీ మేఘాల మధ్య గాలి విద్యుత్ బంధకంగా పనిచేస్తుంది.
5. మేఘాలపై అధిక మొత్తంలో పోగుపడిన ఆవేశాల బదిలీని గాలి విద్యుత్ బంధకం అయినప్పటికీ నిరోధించలేదు.
6. అధిక ధన, ఋణ ఆవేశాలు గల మేఘాల మధ్య విద్యుత్ ఉత్సర్గం జరిగి పెద్ద ఎత్తున వెలుగుతో పాటు ధ్వని ఉత్పత్తి అవుతుంది.
7. ఏర్పడే వెలుగును మెరుపు అని, వెలువడే ధ్వనిని ఉరుము అని అంటారు.

ప్రశ్న 3.
వివిధ రిక్టర్ స్కేలు అవధుల విలువలకు భూకంప ప్రభావం ఏ విధంగా ఉంటుందో రాయండి.
జవాబు:

ప్రశ్న 4.
తరచుగా భూకంపాలు వచ్చే ప్రాంతాలలో భవన నిర్మాణంలో మరియు భూకంప నష్ట తీవ్రతను తగ్గించుటకు తీసుకోవలసిన జాగ్రత్తలను రాయండి.
జవాబు:

1. భవన నిర్మాణాల సలహాలకై ఇంజనీర్లను, ఆర్కిటెక్ట్ ను సంప్రదించాలి.
2. భూకంపాలు ఎక్కువగా వచ్చే అవకాశం ఉన్న ప్రాంతాలలో మట్టి, కలప వినియోగించి నిర్మాణాలు చేయాలి.
3. భవనాల పై భాగం తేలికగా ఉంటే అవి పడినపుడు నష్టం తక్కువగా ఉంటుంది.
4. ఇంటి గోడలకు అల్మరాలను ఏర్పాటుచేయడం మంచిది. అవి త్వరగా పడిపోవు.
5. గోడలకు వేలాడదీసిన వస్తువుల పట్ల జాగ్రత్తగా ఉండాలి. భూకంప సమయంలో అవి మీద పడే అవకాశం ఉంది.
6. భూకంపాలు వచ్చిన సందర్భంలో అగ్నిప్రమాదాలు సంభవించే అవకాశం ఉంది. అందువల్ల విద్యుత్ పరికరాలు, తీగలు నాణ్యమైనవి వినియోగించాలి. పెద్ద భవనాలలో అగ్నిప్రమాద నిరోధక పరికరాలను ఏర్పాటు చేసుకోవాలి.

ప్రశ్న 5.
భారతదేశంలో గతంలో వచ్చిన భూకంపాలు ఎక్కడ వచ్చాయో వివరించండి.
జవాబు:

1. డిసెంబరు 26, 2004లో వచ్చిన సునామి వలన అండమాన్ మరియు నికోబార్‌లో పెద్ద ఎత్తున ఆస్తి, ప్రాణ నష్టం జరిగింది.
2. ఉత్తర కాశ్మీర్ లోని ఉరి, తంగదర్ పట్టణాలలో అక్టోబరు 8, 2005న సంభవించిన భూకంపం భారతదేశంలో అతి పెద్దది.
3. జనవరి 26,2001లో గుజరాత్ లోని భుజ్ జిల్లాలో పెద్ద భూకంపం సంభవించింది. ఈ భూకంపం తీవ్రత 7.7 రిక్టరు స్కేలు నమోదు చేసింది.
4. మే 22, 1997లో మధ్యప్రదేశ్ లోని జబల్ పూర్ లో భూకంపం వచ్చింది. భూకంప తీవ్రత 6గా రిక్టర్ స్కేలు నమోదు చేసింది.
5. సెప్టెంబర్ 30, 1993లో మహారాష్ట్రలోని లాతూర్ (కిల్లరి) లో భూకంపం వచ్చింది.

ప్రశ్న 6.
భూకంప తీవ్రతను కొలిచే పరికరం యొక్క పటాన్ని గీయుము. ఇందులో ఉపయోగించే స్కేలు పేరు తెలుపుము.
జవాబు:

భూకంప తీవ్రతను కొలిచే పరికరంలో ఉపయోగించే స్కేలు : రిక్టర్ స్కేలు.

ప్రశ్న 7.
“భూకంపాల వలన వరదలు, కొండ చరియలు విరిగి పడటం మరియు సునామిలు రావడం వంటివి జరుగుతాయి. డిసెంబర్ 26, 2004 నాడు హిందూ మహాసముద్రంలో సునామి వచ్చింది. దీని వల్ల తూర్పు తీరప్రాంతం తీవ్ర ఆసి, ప్రాణ నష్టం సంభవించింది.” ఈ సమాచారం ఆధారంగా క్రింది ప్రశ్నలకు జవాబులు రాయండి.
1. సునామీ సంభవించడానికి కారణమేమి?
జవాబు:
భూకంపాలు

2. తీవ్ర సునామీ సంభవించినపుడు ఏమి జరుగుతుంది?
జవాబు:
భారీ వర్షాలు, వరదలు, ఆస్తి నష్టం, ప్రాణ నష్టం జరుగుతుంది.

3. భూకంపాన్ని గుర్తించుటకు ఉపయోగించే పరికరం ఏది? దానిలోని ప్రధాన భాగాలేవి?
జవాబు:
భూకంప లేఖిని (సిస్మో గ్రాఫ్) లేదా భూకంప దర్శిన్ని (సిస్మో స్కోప్)
ముఖ్య భాగాలు : గుండ్రంగా తిరిగే డ్రమ్, లోలకం, అయస్కాంతం, తీగ.

4. భూకంప తీవ్రతను సూచించు స్కేలు 8 దాటితే దాని ప్రభావం ఎలా ఉంటుంది?
జవాబు:
తీవ్ర నష్టం (100 కి.మీ.ల విస్తీర్ణంలో)

8th Class Physics 11th Lesson కొన్ని సహజ దృగ్విషయాలు 1 Mark Bits Questions and Answers

బహుళైచ్ఛిక ప్రశ్నలు

I. సరియగు జవాబును ఎంచుకోండి.

1. ఏ శాస్త్రవేత్త, ఏ సంవత్సరంలో వెంట్రుకలు బట్టలను ఆకర్షించటం మరియు ఆకాశంలో మెరుపులూ రెండూ ఒకే దృగ్విషయమని తెలియజేశాడు?
A) 1762 రూథర్ ఫర్డ్
B) 1752 బెంజిమన్ ఫ్రాంక్లిన్
C) 1772 ఫారడే
D) 1782 జాన్ డాల్టన్
జవాబు:
B) 1752 బెంజిమన్ ఫ్రాంక్లిన్

2. భూమిలోని పలకల కదలికల వలన లేదా ఢీకొనుట వలన …………. ఏర్పడును.
A) భూకంపాలు
B) అగ్నిపర్వతాల ప్రేలుడు
C) పిడుగుపాటు
D) ఉరుములు
జవాబు:
A) భూకంపాలు

3. భారతదేశంలో అతిపెద్ద భూకంపం ఇక్కడ సంభవించింది.
A) గుజరాత్ లోని భుజ్ జిల్లాలో
B) ఆంధ్రప్రదేశ్ లోని ఆదిలాబాద్ జిల్లాలో
C) ఉత్తర కాశ్మీర్ లోని ఉరితంగదర్ పట్టణాలలో
D) మధ్యప్రదేశ్ లోని ఉత్తర ప్రాంతంలో
జవాబు:
C) ఉత్తర కాశ్మీర్ లోని ఉరితంగదర్ పట్టణాలలో

4. ఆవేశం కలిగి ఉన్న వస్తువు నుండి భూమికి ఆవేశాలను బదిలీ చేసే ప్రక్రియను ……. అంటారు.
A) ఎర్తింగ్
B) మెరుపులు
C) ఉరుములు
D) ఏదీకాదు
జవాబు:
A) ఎర్తింగ్

5. భూకంప తీవ్రతను కొలవడానికి ఉపయోగించే ప్రమాణం
A) భూకంప స్కేలు
B) రిక్టరు స్కేలు
C) ఐరన్ స్కేలు
D) టేపు
జవాబు:
B) రిక్టరు స్కేలు

6. భూకంప తీవ్రతను కొలవడానికి ఉపయోగించే పరికరం ………….
A) భూకంపలేఖిని
B) రిక్టర్ స్కేలు
C) ఎర్తింగ్
D) పైవన్నీ
జవాబు:
A) భూకంపలేఖిని

7. ఈ కింది వానిలో సహజ దృగ్విషయం కానిది
A) భూకంపం
B) తుపాన్
C) ఉరుములు, మెరుపులు
D) ఎర్తింగ్
జవాబు:
D) ఎర్తింగ్

8. వస్తువులను ఒకదానితో మరొకటి రుద్దడం వలన ఏర్పడే ఆవేశాల సంఖ్య
A) 2
B) 1
C) 3
D) 4
జవాబు:
A) 2

9. సునామి అంటే అర్థం
A) భూకంపం
B) తుపాను
C) సముద్రం అడుగున భూకంపం
D) సముద్రం అడుగున అగ్నిపర్వతం పేలుట
జవాబు:
D) సముద్రం అడుగున అగ్నిపర్వతం పేలుట

10. భూమి నుండి ఉత్పత్తి అయ్యే తరంగాలను ……….. అంటారు.
A) భూకంప తరంగాలు
B) మైక్రో తరంగాలు
C) రేడియో తరంగాలు
D) X-తరంగాలు
జవాబు:
A) భూకంప తరంగాలు

11. ఆవేశపూరిత వస్తువు పరీక్షించడానికి ఉపయోగపడే ధర్మం
A) ఆకర్షణ
B) వికర్షణ
C) ఆకర్షణ మరియు వికర్షణ
D) ఏదీకాదు
జవాబు:
B) వికర్షణ

12. రెండు వస్తువులు ఒకదానితో మరొకటి రుద్దినపుడు ఆ వస్తువులపై ఏర్పడే ఆవేశాలు
A) సమానంగా ఉండే ఒకే రకమైన ఆవేశాలు
B) సమానంగా ఉండే వేరు వేరు ఆవేశాలు
C) అసమానంగా ఉండే ఒకే రకమైన ఆవేశాలు
D) అసమానంగా ఉండే వేరు వేరు ఆవేశాలు
జవాబు:
B) సమానంగా ఉండే వేరు వేరు ఆవేశాలు

13. రిక్టరు స్కేలు విలువ ……. గా ఉన్నప్పుడు భూకంప లేఖిని నమోదు చేస్తుంది కాని మనం గుర్తించలేము
A) 3.5 నుండి 5.4
B) 5. 5 నుండి 6.00
C) 3. 5 కన్నా తక్కువ
D) 8 కన్నా ఎక్కువ
జవాబు:
C) 3. 5 కన్నా తక్కువ

14. …………… వరకు రిక్టరు స్కేలు విలువ ఉంటే ఆస్తి మరియు ప్రాణనష్టం అధికంగా ఉంటుంది. దీనిని పెద్ద భూకంపాలు అంటారు.
A) 5. 5 నుండి 6.0
B) 6.1 నుండి 6.9
C) 7.0 నుండి 7.9
D) 3.5 నుండి 5.4
జవాబు:
C) 7.0 నుండి 7.9

15. ఒక వస్తువు ఆవేశపరచే పద్ధతులు ………
A) రాపిడి (రుద్దడం) వలన
B) ప్రేరణ వలన
C) వాహకం ద్వారా
D) పైవన్నీ
జవాబు:
D) పైవన్నీ

16. ఉరుములు, మెరుపులు వచ్చే సందర్భంలో సురక్షితమైన ప్రదేశం
A) తక్కువ ఎత్తుగల ఇల్లు
B) ఎత్తైన భవనం
C) పొడవైన చెట్టు
D) టాప్ లేని కారులో ప్రయాణించడం
జవాబు:
A) తక్కువ ఎత్తుగల ఇల్లు

17. ఉరుములు, మెరుపులు వచ్చే సందర్భంలో సురక్షితం కాని ప్రదేశం
A) తక్కువ ఎత్తుగల ఇల్లు
B) పొట్టి చెట్టు
C) ఎలక్ట్రికల్, టెలిఫోన్ స్తంభాల దగ్గర నిలబడటం
D) ఏదీకాదు
జవాబు:
C) ఎలక్ట్రికల్, టెలిఫోన్ స్తంభాల దగ్గర నిలబడటం

18. భూకంపం వచ్చినపుడు భూమి కంపించిన సమయాన్ని గుర్తించేది
A) భూకంపలేఖిని
B) భూకంప దర్శిని
C) భ్రామపరిమాణ స్కేలు
D) రిక్టర్ స్కేలు
జవాబు:
B) భూకంప దర్శిని

19. భూకంపాలను ……….. ద్వారా కచ్చితంగా నిర్ధారించవచ్చును.
A) రిక్టర్ స్కేలు
B) భ్రామక పరిమాణ స్కేలు
C) మీటరు స్కేలు
D) పైవన్నీ
జవాబు:
B) భ్రామక పరిమాణ స్కేలు

20. ఇంటి లోపల ఉన్నప్పుడు భూకంపం వచ్చిన సందర్భంలో రక్షించుకోవడం కోసం
A) పొడవైన వస్తువులను గట్టిగా పట్టుకోవడం
B) మంచంపై పడుకోవడం
C) బల్ల కిందకు వెళ్ళడం
D) పైవన్నీ
జవాబు:
C) బల్ల కిందకు వెళ్ళడం

21. సీమగుగ్గిలంను ఉన్నితో రుద్దిన తర్వాత అది వెంట్రుకలను ఆకర్షించునని గుర్తించిన వారు
A) సిక్కులు
B) యూరోపియన్లు
C) అమెరికన్లు
D) గ్రీకులు
జవాబు:
D) గ్రీకులు

22. విద్యుత్ ఆవేశాల లక్షణాల విషయంలో
A) ప్లాస్టిక్ స్కేలును తలపై రుద్దితే అది చిన్న చిన్న కాగితం ముక్కలను ఆకర్షించడం
B) పొడిజుట్టుతో ప్లాస్టిక్ స్కేలును రుద్దిన అది చిన్న చిన్న కాగితం ముక్కలను ఆకర్షించకుండుట
C) గాలితో నిండిన బెలూనను బట్టతో రుద్దిన అది కాగితం ముక్కలను ఆకర్షించుట
D) స్ట్రాను నునుపైన గోడకు గాని, బట్టలకు గాని అది కాగితం ముక్కలను ఆకర్షించుట
జవాబు:
B) పొడిజుట్టుతో ప్లాస్టిక్ స్కేలును రుద్దిన అది చిన్న చిన్న కాగితం ముక్కలను ఆకర్షించకుండుట

23. ఉన్ని గుడ్డతో రుద్దిన బెలూన్, ఉన్నిగుడ్డతో రుద్దిన మరో బెలూనన్ను …….
A) ఆకర్షించును
B) వికర్షించును
C) A మరియు B
D) ఏదీకాదు
జవాబు:
B) వికర్షించును

24. పాలిథిన్ కాగితంతో రుద్దిన రీఫిల్ అదే కాగితంతో రుద్దిన మరో రీఫిల్ ను ………..
A) ఆకర్షించును
B) వికర్షించును
C) A మరియు B
D) ఏదీకాదు
జవాబు:
B) వికర్షించును

25. ఉన్నిగుడ్డతో రుద్దిన బెలూన్, పాలిథిన్ కాగితంతో రుద్దిన రీఫిల్ ను ……….
A) ఆకర్షించును
B) వికర్షించును
C) A మరియు B
D) ఏదీకాదు
జవాబు:
A) ఆకర్షించును

26. విజాతి అయస్కాంతాల ధృవాలు
A) ఆకర్షించును
B) వికర్షించును
C) A మరియు B
D) ఏదీకాదు
జవాబు:
A) ఆకర్షించును

27. సజాతి అయస్కాంతాల ధృవాలు
A) ఆకర్షించును
B) వికర్షించును
C) A మరియు B
D) ఏదీకాదు
జవాబు:
B) వికర్షించును

28. ఒకే రకమైన రెండు ఆవేశాలు
A) ఆకర్షించును
B) వికర్షించును
C) A మరియు B
D) ఏదీకాదు
జవాబు:
B) వికర్షించును

29. విభిన్నాలైన రెండు ఆవేశాలు
A) ఆకర్షించును
B) వికర్షించును
C) A మరియు B
D) ఏదీకాదు
జవాబు:
A) ఆకర్షించును

30. వలయంలో విద్యుత్ ప్రవాహం …… కదలికను తెలుపును.
A) ఆవేశాల
B) ప్రోటానుల
C) న్యూట్రానుల
D) ఏదీకాదు
జవాబు:
A) ఆవేశాల

31. దీనినుపయోగించి వస్తువు ఆవేశాన్ని కల్గి ఉన్నది లేనిది తెలుసుకోవచ్చును
A) దిక్సూచి
B) థర్మోకోల్ బంతి
C) విద్యుదర్శిని
D) ఏదీకాదు
జవాబు:
C) విద్యుదర్శిని

32. వస్తువుపై గల ఆవేశాలు భూమికి బదిలీ అయ్యే పద్ధతిని ………. చేయటం అంటాము.
A) మెరుపు
B) ఉరుము
C) ఎర్తింగ్
D) ఆవేశము
జవాబు:
C) ఎర్తింగ్

33. గాలిలో మేఘాలు ప్రయాణించేటప్పుడు, గాలిలోని కణాలతో ఈ క్రింది ప్రక్రియ వలన ఆవేశపూరితం అవుతాయి.
A) బలం
B) శక్తి రుద్దిన
C) ఘర్షణ
D) స్థానభ్రంశం
జవాబు:
C) ఘర్షణ

34. ఒక ఆవేశపూరిత మేఘానికి దగ్గరగా మరొక మేఘం వచ్చినప్పుడు అది రెండవ మేఘంపై ……. ఆవేశాన్ని ప్రేరేపింపజేయును.
A) సమాన
B) వ్యతిరేక
C) తుల్య
D) ఏదీకాదు
జవాబు:
B) వ్యతిరేక

35. రెండు మేఘాల మధ్య గాలి …….. వాహకంగా పని చేయును.
A) అథమ విద్యుత్
B) ఉత్తమ విద్యుత్
C) మధ్యమ విద్యుత్
D) ఋణ విద్యుత్
జవాబు:
A) అథమ విద్యుత్

36. మెరుపులు ఏర్పడు ప్రక్రియను………….. అంటారు.
A) విద్యుత్ ఉత్సర్గం
B) విద్యుత్ ప్రవాహం
C) A మరియు B
D) ఏదీకాదు
జవాబు:
A) విద్యుత్ ఉత్సర్గం

37. కింది వాటిలో ఉరుములు, మెరుపులతో కూడిన వర్షం వచ్చు సందర్భంలో సురక్షితం కాని ప్రదేశం
A) టాప్ లేని వాహనాల్లో ప్రయాణించటం
B) ల్యాండ్ లైన్ ఫోన్లలో మాట్లాడడం
C) టి.వి., కంప్యూటర్ వంటి పరికరాలు వాడటం
D) పైవన్నియూ
జవాబు:
D) పైవన్నియూ

38. తటిద్వాహకాలను వీటి రక్షణ కొరకై భవనాల్లో అమర్చుతారు
A) పిడుగుల నుండి
B) భూకంపాల నుండి
C) తుపానుల నుండి
D) ఆవేశాల నుండి
జవాబు:
A) పిడుగుల నుండి

39. క్రింది వాటిలో సహజ దృగ్విషయాల విషయంలో విభిన్నమైనది
A) మెరుపులు, ఉరుములు
B) వరదలు, తుపానులు
C) భూకంపాలు
D) ఋతుపవనాలు
జవాబు:
D) ఋతుపవనాలు

40. భూ పొరలలో అన్నింటికన్నా పెద్దది
A) భూపటలం
B) భూప్రావారం
C) అంతర కోర్
D) బాహ్య కోర్
జవాబు:
A) భూపటలం

41. భుజ్, కాశ్మీర్‌లో వచ్చిన భూకంప తీవ్రత విలువ
A) < 6.5
B) < 7.5
C) > 7.5
D) > 6.5
జవాబు:
C) > 7.5

42. సెస్మిక్ తరంగాలను దీని ద్వారా గుర్తిస్తారు
A) థర్మామీటరు
B) భూకంపలేఖిని
C) విద్యుద్దర్శిని
D) ఉత్సర్గ నాళం
జవాబు:
B) భూకంపలేఖిని

43. ‘భూకంప తీవ్రతను కచ్చితంగా కొలుచు పరికరం
A) భూకంపలేఖిని
B) భ్రామక పరిమాణ స్కేలు
C) విద్యుద్దర్శిని
D) థర్మామీటరు
జవాబు:
B) భ్రామక పరిమాణ స్కేలు

44. భూకంప ప్రమాద పటం ప్రకారం ఆంధ్రప్రదేశ్ లోని 3వ జోన్ కి చెందు ప్రాంతము
A) కృష్ణా, గోదావరి మైదానం
B) కడప, చిత్తూరు
C) నెల్లూరు
D) అన్నియూ
జవాబు:
D) అన్నియూ

45. ఈ క్రింది వానిలో భూకంపాలు రాని ఖండం
A) అమెరికా
B) ఆసియా
C) ఆస్ట్రేలియా
D) ఏదీలేదు
జవాబు:
C) ఆస్ట్రేలియా

46. రిక్టర్ స్కేల్ ను కనుగొన్నవారు
A) ఛార్లెస్ లూయీస్
B) జేమ్స్ ఛార్లెస్
C) ఛార్లెస్ రిక్టర్
D) ఛార్లెస్ రెపో
జవాబు:
C) ఛార్లెస్ రిక్టర్

47. ఈ క్రింది భూకంప జోన్లో తీవ్ర ప్రమాదకరమైనది
A) 1వ జోన్
B) 3వ జోన్
C) 7వ జోన్
D) 5వ జోన్
జవాబు:
D) 5వ జోన్

48. సునామీల యొక్క వేగం సముద్ర అంతర్భాగంలో ………….. వద్ద ఏర్పడును.
A) 700
B) 600
C) 800
D) 900
జవాబు:
C) 800

49. సముద్రంలో ఏర్పడు భూకంపంకు గల పేరు
A) సునామీ
B) తుపాను
C) వాయుగుండం
D) భూకంపం
జవాబు:
A) సునామీ

50. ర్యాపిడ్ అనే సెట్ డిజాస్టర్‌కు ఉదాహరణ
A) సునామీ
B) తుపాను
C) వాయుగుండం
D) భూకంపం
జవాబు:
D) భూకంపం

51. మన దేశంలో భూకంప తీవ్రత జోన్-8 లోనికి చెందు ప్రాంతము
A) ఉత్తరప్రదేశ్
B) హిమాలయాల చుట్టూ ప్రాంతం
C) గుజరాత్
D) కాశ్మీర్
జవాబు:
B) హిమాలయాల చుట్టూ ప్రాంతం

52. భారతదేశ రాష్ట్రాల్లో తుపానులకు అధికంగా గురయ్యే రాష్ట్రం
A) ఒడిశా
B) అస్సోం
C) గుజరాత్
D) ఆంధ్రప్రదేశ్
జవాబు:
A) ఒడిశా

53. పశ్చిమ తీరంలో తుపాన్లకు గురయ్యే రాష్ట్రం
A) ఒడిశా
B) అస్సోం
C) గుజరాత్
D) ఆంధ్రప్రదేశ్
జవాబు:
C) గుజరాత్

54. బెలూన్ ప్లాస్టిక్ కాగితంతో రుద్ది, చిన్న కాగితం ముక్కల వద్దకు తెచ్చినప్పుడు ఏమి పరిశీలిస్తావు?
A) బెలూన్ కాగితం ముక్కలను ఆకర్షిస్తుంది.
B) బెలూన్ కాగితం ముక్కలను ఆకర్షించదు.
C) బెలూన్ పగిలిపోతుంది.
D) బెలూన్ పరిమాణంలో మార్పు వస్తుంది.
జవాబు:
A) బెలూన్ కాగితం ముక్కలను ఆకర్షిస్తుంది.

55. ప్లాస్టిక్ స్కేలును ప్లాస్టిక్ కాగితంతో రుద్ది చిన్న కాగితం ముక్కల వద్దకు తీసుకొని వస్తే అవి ఆకర్షించబడతాయి.
A) స్థావర విద్యుత్ బలం
B) అయస్కాంత బలం
C) గురుత్వాకర్షణ బలం
D) జ్వలన ఉష్ణోగ్రత
జవాబు:
A) స్థావర విద్యుత్ బలం

56. ఉరుములు, మెరుపులతో కూడిన వర్షం సంభవించునపుడు సురక్షిత ప్రదేశం
1) బహిరంగ ప్రదేశాలలో ప్రయాణించడం.
2) పొడవాటి వృక్షాల కింద నిలబడడం.
3) విద్యుత్ స్థంబాల వద్ద నిలబడడం.
4) కిటికీలు మూసిన కారులో కూర్చోవడం.
A) 1 మాత్రమే
B) 1 & 4
C) 2 & 3
D) 1 మాత్రమే
జవాబు:
A) 1 మాత్రమే

57. రేవతి ఒక రబ్బరు బెలూన్ ను ఉన్ని గుడ్డతోను, రీఫిలను పాలిథీన్ తోను రుద్దినది. తర్వాత బెలూనను రీఫిల్ వద్దకు తెచ్చినపుడు సరైన పరిశీలన
A) రీఫిల్ వికర్షించును
B) రీఫిల్ ఆకర్షించును
C) బెలూన్ మరియు రీఫిల మధ్య బలం పనిచేయదు.
D) చెప్పలేము.
జవాబు:
B) రీఫిల్ ఆకర్షించును

58. రెండు విద్యుదావేశం చెందిన వస్తువులను దగ్గరగా తెచ్చినపుడు అవి
A) ఆకర్షించుకోవచ్చు
B) వికర్షించుకోవచ్చు
C) ఆకర్షించుకోవచ్చు లేదా వికర్షించుకోవచ్చు
D) ఏ విధమైన ప్రభావం ఉండదు.
జవాబు:
C) ఆకర్షించుకోవచ్చు లేదా వికర్షించుకోవచ్చు

59. భూమి యొక్క బాహ్య పొరను కింది విధంగా చెప్తారు
A) భూపటలం (మాంటిల్)
B) బాహ్య కేంద్రం
C) భూప్రావరం (క్రస్ట్)
D) అంతర కేంద్రం
జవాబు:
A) భూపటలం (మాంటిల్)

60. భూకంపానికి కారణమైన భూమి యొక్క ఫలకము
A) భూపటలం
B) భూప్రావరం
C) భూఅంతర కేంద్రం
D) భూ బాహ్య కేంద్రం
జవాబు:
B) భూప్రావరం

61. కింది వానిలో ఏది సునామీకి కారణం కాదు?
A) సముద్రం అడుగున అతి పెద్ద కేంద్రక విస్పోటనం
B) భూకంపం
C) అగ్నిపర్వతం విస్పోటనం.
D) పిడుగు
జవాబు:
D) పిడుగు

62. రాజేష్ ఒక బెలూనను ఊది దాని చివర ముడివేశాడు. ఒక కాగితాన్ని చిన్న చిన్న ముక్కలుగా చేసి గచ్చు పై వేసాడు. తర్వాత బెలూనను ఒక చేతితో బాగా రుద్ది కాగితం ముక్కల వద్దకు తెచ్చాడు. అపుడు కాగితం ముక్కలను బెలూన్ ఆకర్షించింది. ఆ కృత్యం చేయడం వలన రాజేష్ క్రింది విషయాన్ని తెలుసుకున్నాడు.
i)స్పర్శాబలం పనిచేయాలంటే వస్తువులు ఒకదాని కొకటి తాకనవసరం లేదు.
ii) బెలూనను కాగితంతో రుద్దినపుడు దాని ఉపరితలం విద్యుదావేశం పోతుంది.
iii) క్షేత్రబలం పనిచేయాలంటే వస్తువులు ఒకదాని కొకటి తాకనవసరం లేదు.
A) ii మాత్రమే సరైనది
B) i మరియు ii మాత్రమే సరైనవి
C) ii మరియు iii మాత్రమే సరైనవి
D) i మాత్రమే సరైనది
జవాబు:
C) ii మరియు iii మాత్రమే సరైనవి

II. జతపరచుము.

జవాబు:

2)

జవాబు: