Class 7

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 7 Data Handling Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson Data Handling Exercise 2

Question 1.
Long jumps by 7 students of a team are 98cm, 125cm, 140cm, 155cm, 174cm, 140cm and 155cm. Find the mode of the data.
Solution:
The given datais 98cm, 125 cm, 140 cm, 155 cm. 174 cm, 140 cm, 155 cm.
Most frequently appearedobservations (i.e.,) mode is 140 cm and 155 cm.

Question 2.
Ages of players in a cricket team are 25, 26, 25, 27, 28, 30, 31, 27, 33, 27, 29.
(i) Find the mean and mode of the data.
(ii) Find the minimum number of players to be added to the above team so that mode of the data changes and what must be their ages.
Solution:
i) Given that the ages of players of a cricket team are 25, 26. 25. 27. 28. 30, 3i. 27. 33, 27, 29
Mean = \(\frac{\text { Sum of the ages }}{\text { Number of players }}\)
= \(\frac{25+26+25+27+28+30+31+27+33+27+29}{11}=\frac{308}{11}\) = 28
Mode = frequently appeared = 27
ii) To change the mode minimum two players of age 25 must be added.

Question 3.
Find the mode of the following data. 12,24,36,46,25,38, 72, 36,25,38, 12,24,46, 25, 12, 24, 46, 25, 72, 12, 24, 36,25, 38 and 36.
Solution:

Question 4.
Decide whether mean or mode is a better representative value
in the following situations.
(i) A shop keeper, who sells tooth paste tubes of different sizes, wants to decide which size to is be ordered more.
(ii) An invigilator wants to bring sufficient number of additional papers to the examination
hath
(iii) Preparation of the number of laddus for a marriage.
(iv) For finding the favorite cricketer in a class.

Solution:
i) Mode
ii) Mean
iii) Mean
iv) Mode

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 3 Simple Equations Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 3rd Lesson Simple Equations Exercise 1

Question 1.
Write L.H.S and R.H.S of the following simple equations.
(i) 2x = 10
(ii) 2x – 3 = 9
(iii) 4z + 1 = 8
(iv) 5p + 3 = 2p + 9
(v) 14 = 27 – y
(vi) 2a – 3 = 5
(vii) 7m = 14
(viii) 8 = q + 5
Solution:

Question 2.
Solve the following equations by trial and error method.
(i) 2 + y = 7
(ii) a – 2 = 6
(iii) 5m = 15
(iv) 2n = 14
Solution:
(i) 2 + y = 7
if y = 1; LHS = 2 + y = 2 + 1 = 3 ≠ 7
If y = 2; LHS = 2 + 2 = 4 ≠ 7
If y = 3; LHS = 2 + 3 = 5 ≠ 7
If y = 4; LHS = 2 + 4= 6 ≠ 7
If y = 5; LHS = 2 + 5 = 7 = 7 = RHS
∴ y = 5 is the solution of 2 + y = 7

(ii) a – 2 = 6
As a – 2 = 6 ; the value of ‘a’ must be greater than 6.
If a = 7; LHS = 7 – 2 = 5 ≠ 6
If a = 8; LHS = 8 – 2 = 6 = RHS
∴ a = 8 is the solution of a – 2 = 6

(iii) 5m = 15
If m = 1 then LHS = 5 × 1 = 5 ≠ b15
m = 2 then LHS = 5 × 2 = 10 ≠ 15
m = 3 then LHS = 5 × 3 = 15 = 15
∴ m = 3 is the solution of 5m = 15

(iv) 2n = 14
If n = 1 then LHS = 2 × 1 = 2 ≠ 14
n = 2 then LHS = 2 × 2 = 4 ≠ 14
n = 3 then LHS = 2 × 3 = 6 ≠ 14
n = 4 then LHS = 2 × 4 = 8 ≠ 14
n = 5 then LHS = 2 × 5 = 10 ≠ 14
n = 6 then LHS = 2 × 6 = 12 ≠ 14
n = 7 then LHS = 2 × 7 = 14 ≠ 14
∴ n = 7 is the solution of 2n = 14

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 2 Fractions, Decimals and Rational Numbers Ex 7 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 2nd Lesson Fractions, Decimals and Rational Numbers Exercise 7

Question 1.
Write any three equivalent rational numbers to each of the following
i) \(\frac { 2 }{ 3 }\)
ii) \(\frac { -3 }{ 8 }\)
Solution:

Question 2.
What is the equivalent rational number for \(\frac { -15 }{ 36 }\) with
(i) denominator 12
(ii) numerator 75?
Solution:
i) \(\frac{-15}{36}=\frac{-15 \div 3}{36 \div 3}=\frac{-5}{12}\)
ii) \(\frac{-15}{36}=\frac{-15 \times 5}{36 \times 5}=\frac{-75}{180}\)

Question 3.
Mark the following rational numbers on the number line.
(i) \(\frac { 1 }{ 2 }\)
(ii) \(\frac { 3 }{ 4 }\)
(iii) \(\frac { 3 }{ 2 }\)
(iv) \(\frac { 10 }{ 3 }\)
Solution:

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 7 Data Handling Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson Data Handling Exercise 1

Question 1.
Maximum day time temperatures of Hyderabad in a week (from 26th February to 4th March, 2011) are recorded as 26°C, 27°C, 30°C, 30°C, 32°C, 33°C and 32°C.
(i) What is the maximum temperature of the week?
(ii) What is the average temperatures of the week?
Solution:
i) Maximum temperature = 33C
ii) Average temperature = \(\frac{\text { Sum of the temperatures }}{\text { No. of observations }}\)
= \(\frac{26+27+30+30+32+33+32}{7}=\frac{210}{7}\)
∴ The average temperature of the week 30°C.

Question 2.
Rice consumed in a school under the mid-day meal program for 5 consecutive days is 15.750 kg, 14.850 kg, 16.500 kg, 14.700 kg, and 17.700 kg. Find the average rice consumption for the 5 days.

Solution:
Rice consumed for 5 days in kg = 15.750, 14.850, 16.500 14.700, 17.700

∴ The average rice consumption for the 5 days = 15.900 kg.

Question 3.
In a village three different crops are cultivated in four successive years. The profit (in rupees) on the crops, per acre is shown in the table below-

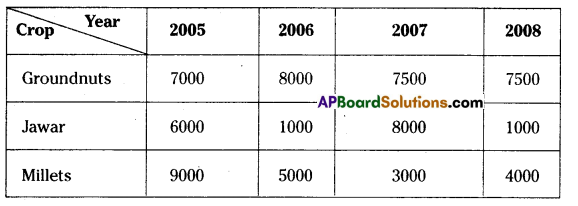
(i) Calculate the mean profit for each crop over the 4 years.
(ii) Based on your answers, which crop should be cultivated in the next year?
Solution:

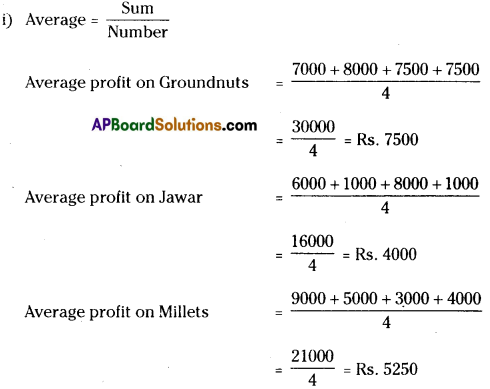
(ii) As the mean profit on Groundnuts is more than the other two crops, Groundnuts may be cultivated for the next year.

Question 4.
The number of passengers who travelled in APSRTC bus from Adilabad to Nirmal in 4 trips in a day are 39, 30, 45 and 54. What is the occupancy ratio (average number of passengers travelling per trip) of the bus for the day?

Solution:
Passengers travelled in 4 days 39. 30, 45 and 54
Average / Occupancy ratio = \(\frac{\text { Sum }}{\text { Number }}=\frac{\text { Total passengers travelled }}{\text { Number of days }}\)
= \(\frac{39+30+45+54}{4}=\frac{168}{4}=42\)
∴ The occupancy ratio of the bus for the day = 42

Question 5.
The following table shows the marks scored by Anju, Neelesh and Lckhya in four unit tests of English.

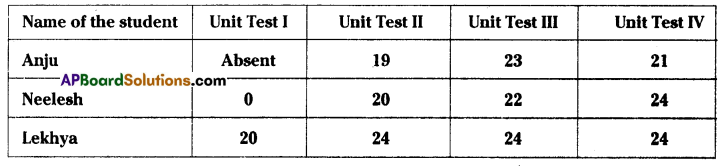
(i) Find the average marks obtained by Lekhya.
(ii) Find the average marks secured by Anju. Will you divide the total marks by 3 or 4?Why?
(iii) Neelesh has given all four tests. Find the average marks secured by him. Will you divide the total marks by 3 or 4? Why?
(iv) Who performed best in the English?
Solution:
Average = \(\frac{\text {Sum of the observations }}{\text { Number of observations }}\)
i) Average marks obtained by Lekhya = \(\frac{20+24+24+24}{4}=\frac{92}{4}\) = 23
ii) Anju has given only three tests. So to find the average marks we divide by 3.
(i.e.) average = \(\frac{19+23+21}{3}=\frac{63}{3}\) = 21
iii) Neelesh has given 4 tests. So to find the average marks we divide by 4.
(i.e.) average = \(\frac{0+20+22+24}{4}=\frac{66}{4}\) = 16.5
iv) As the average marks of Lekhya is greater than the other two, we conclude that Lekhya
performed best in English.

Question 6.
Three friends went to a hotel and had breakfast to their taste, paying 16, 17 and 21 respectively
(i) Find their mean expenditure.
(ii) If they have spent 3 times the amount that they have already spent, what would their mean expenditure be?
(iii) If the hotel manager offers 50% discount, what would their mean expenditure be?
(iv) Do you notice any relationship between the change in expenditure and the change in mean expenditure.
Solution:
i) Mean expenditure = \(\frac{\text { Total expenditure }}{\text { No. of persons }}\)
= \(\frac{16+17+21}{3}=\frac{54}{3}\) = Rs. 18

ii) Amount spent = 3 times I.e., 3 × 16; 3 × 17; 3 × 21
= Rs. 48; Rs. 51; Rs. 63
Now the average = \(\frac{48+51+63}{3}=\frac{162}{3}\) = Rs. 54 = 3 x original average

iii) After 50% discount the amount spent is Half of the actual amount = \(\frac{16}{2}, \frac{17}{2}, \frac{21}{2}\)
= Rs.8; Rs. 8.50; Rs. 10.50
Now the average = \(\frac{8+8.50+10.50}{3}=\frac{27.00}{3}\) = Rs .9 = \(\frac{\text { Original average }}{2}\)

iv) The change In the observations is also carried out in the mean.

Question 7.
Find the mean of the first ten natural numbers.
Solution:
First ten natural numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10
∴ Average = \(\frac{\text { Sum of the numbers }}{\text { Number }}\)
= \(\frac{1+2+3+4+5+6+7+8+9+10}{10}=\frac{55}{10}\) = 5.5
∴ The mean of the first ten natural numbers = 5.5.

Question 8.
Find the mean of the first five prime numbers.
Solution:
First five prime numbers are 2, 3, 5, 7 and 11
Average of first five prime numbers = \(\frac{\text { Sum of the numbers }}{\text { Number of primes }}\)
= \(\frac{2+3+5+7+11}{5}=\frac{28}{5}\) = 5.6

Question 9.
In a set of four integers, the average of the two smallest integers is 102, the average of the three smallest integers is 103, the average of all four is 104. Which is the greatest of these integers?
Solution:
Given that
The average of four lntegers = 104 = \(\frac{\text { Sum of the four integers }}{\text { Number of integers }}\)
∴ The sum of the four integers = average × number
= 104 × 4
= 413
Also the average of the three smallest integers = 103 = \(\frac{\text { Sum of the three smallest integers }}{\text { Number of integers }}\)
∴ The sum of the smallest three integers = average × number
= 103 × 3
= 309
∴ The greatest integer / fourth number (Sum of four Integers) – (Sum of three integers)
=416 – 309 = 107

Question 10.
Write at least two questions to find the mean, giving suitable data.
Solution:
Q – 1: The daily income of a shop-keeper during 6 days are Rs. 350, Rs. 325, Rs, 400, Rs. 450, Rs. 600, Rs. 120. Find his average daily income.
Q – 2: The number of eggs sold by a poultry during 5 days are 480, 512, 680, 720 and 1026. Find the average daily sales.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 2 Fractions, Decimals and Rational Numbers Ex 6 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 2nd Lesson Fractions, Decimals and Rational Numbers Exercise 6

Question 1.
Solve the following.
(i) 0.3 × 6
(ii) 7 × 2.7
(iii) 2.71 × 5
(iv) 19.7 × 4
(v) 0.05 × 7
(vi) 210.01 × 5
(vii) 2 × 0.86
Solution:
(i) 0.3 × 6 = 1.8
(ii) 7 × 2.7 = 18.9
(iii) 2.71 × 5 = 13.55
(iv) 19.7 × 4 = 78.8
(v) 0.05 × 7 = 0.35
(vi) 210.01 × 5 = 1050.05
(vii) 2 × 0.86 = 1.72

Question 2.
Find the area of a rectangle whose length is 6.2 cm and breadth is 4 cm.
Solution:
Length of the rectangle = 6.2 cm
Breadth of the rectangle = 4 cm
Area of the rectang’e = Length × Breadth
= 6.2 × 4 = 24.8cm²

Question 3.
Solve the following.
(i) 21.3 × 10
(ii) 36.8 × 10
(ii) 53.7 × 10
(iv) 168.07 × 10
(v) 131.1 × 100
(vi) 156.1 × 100
(vii) 3.62 × 100
(viii) 43.07 × 100
(ix) 0.5 × 10
(x) 0.08 × 10
(xi) 0.9 × 100
(xii) 0.03 × 1000
Solution:
(i) 21.3 × 10 = 213
(ii) 36.8 × 10 = 368
(ii) 53.7 × 10 = 537
(iv) 168.07 × 10 = 1680.7
(v) 131.1 × 100 = 13110
(vi) 156.1 × 100 = 15610
(vii) 3.62 × 100 = 362
(viii) 43.07 × 100 = 4307
(ix) 0.5 × 10 = 5
(x) 0.08 × 10 = 0.8
(xi) 0.9 × 100 = 90
(xii) 0.03 × 1000 = 30

Question 4.
A motor bike covers a distance of 62.5 km.consuming one litre of petrol. How much distance does it cover for 10 litres of petrol?
Solution:
Distance covered for 1 lit, of petrol = 62.5 km
∴ Distance covered for 10 lit, of petrol = 62.5 × 10 = 625 km

Question 5.
Solve the following.
(i) 1.5 × 0.3
(ii) 0.1 × 47.5
(iii) 0.2 × 210.8
(iv) 4.3 × 3.4
(v) 0.5 × 0.05
(vi) 11.2 × 0.10
(vii) 1.07 × 0.02
(viii) 10.05 × 1.05
(ix) 101.01 × 0.01
(x) 70.01 × 1.1
Solution:
(i) 1.5 × 0.3 = 0.45
(ii) 0.1 × 47.5 = 4.75
(iii) 0.2 × 210.8 = 42.16
(iv) 4.3 × 3.4 = 14.62
(v) 0.5 × 0.05 = 0.025
(vi) 11.2 × 0.10 = 1.12
(vii) 1.07 × 0.02 = 0.0214
(viii) 10.05 × 1.05 = 10.5525
(ix) 101.01 × 0.01 = 1.0101
(x) 70.01 × 1.1 = 77.011

Question 6.
Solve the following.
(i) 2.3 ÷ 100
(ii) 0.45 ÷ 5
(iii) 44.3 ÷ 10
(iv) 127.1 ÷ 1000
(v) 7 ÷ 35
(vi) 88.5 ÷ 0.15
(vii) 0.4 ÷ 20
Solution:
(i) 2.3 ÷ 100 = \(\frac{23}{10}\) ÷ 100 = \(\frac{23}{10} \times \frac{1}{100}=\frac{23}{1000}\) = 0.023
(ii) 0.45 ÷ 5 = \(\frac{45}{100}\) ÷ 5 = \(\frac{45}{100} \times \frac{1}{5}=\frac{9}{100}\) = 0.09
(iii) 44.3 ÷ 10 = 44.3 × \(\frac{1}{10}\) = 4.43
(iv) 127.1 ÷ 1000 = 127.1 × \(\frac{1}{1000}\) = 0.1271
(v) 7 ÷ 35 = 7 × \(\frac{1}{3.5}=\frac{7 \times 10}{3.5 \times 10}=\frac{70}{35}\) = 2
(vi) 88.5 ÷ 0.15 = \(\frac{885}{10} \div \frac{15}{100}\) = \(\frac{885}{10} \times \frac{100}{15}\) = 590
(vii) 0.4 ÷ 20 = \(\frac{4}{10}\) ÷ 20 = \(\frac{4}{10} \times \frac{1}{20}=\frac{1}{10 \times 5}=\frac{1}{50}\) = 0.02

Question 7.
A side of a regular polygon is 3.5 cm in length. The perimeter of the polygon is 17.5 cm.
How many sides does the polygon have?
Solution:
Side of each length of the polygon . = 3.5 cm
Total length of all sides = perimeter = 17.5 cm
Number of sides of the polygon = 17.5 + 3.5
= \(\frac{175}{10} \div \frac{35}{10}\) = \(\frac{175}{10} \times \frac{10}{35}\) = 5

Question 8.
A rain fall of 0.896 cm. was recorded in 7 hours, what was the average amount of rain per
hour?
Solution:
Total rainfall recorded in 7 hours = 0896 cm
∴ Average rainfall (for 1 hour) = 0.896 ÷ 7
= \(\frac{896}{1000} \div 7=\frac{896}{1000} \times \frac{1}{7}=\frac{128}{1000}\) = 0.128

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 5 Triangle and Its Properties Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangle and Its Properties Exercise 2

Question 1.
In ΔABC, D is the midpoint of \(\overline{\mathrm{BC}}\)
(i) \(\overline{\mathrm{AD}}\) is the ___________________
(ii) \(\overline{\mathrm{AE}}\) is the ____________________

Solution:
(i) \(\overline{\mathrm{AD}}\) is the median
(ii) \(\overline{\mathrm{AE}}\) is the Altitude

Question 2.
Name the triangle in which the two altitudes of the triangle are two of its sides.
Solution:
In Right angled triangle, the sides containing the right
angle are two altitudes.
In ΔCAT, ∠A = 90° and CA; AT are altitudes.

Question 3.
Does a median always lie in the interior of the triangle?
Solution:
Yes, a median always lie in the interior of the triangle.

Question 4.
Does an altitude always lie in the interior of a triangle’?
Solution:
No, an altitude need not always lie In the interior of a triangle.

Question 5.
(i) Write the side opposite to vertex Y in ΔXYZ.
(ii) Write the angle opposite to side \(\overline{\mathrm{PQ}}\) in ΔPQR.
(iii) Write the vertex opposite to side \(\overline{\mathrm{AC}}\) in ΔABC.
Solution:
i) Side opposite to vertex Y = \(\overline{\mathrm{XZ}}\)
ii) Angle opposite to side \(\overline{\mathrm{PQ}}\) = ∠R
lii) Vertex opposite to side \(\overline{\mathrm{AC}}\) = B

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 5 Triangle and Its Properties Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangle and Its Properties Exercise 1

Question 1.
Is it possible to have a triangle with the following sides?
(i) 3 cm, 4 cm and 5 cm.
(ii) 6 cm, 6 cm and 6 cm.
(iii) 4 cm, 4 cm and 8 cm.
(iv) 3 cm, 5 cm and 7 cm.
Solution:
i) 3 + 4 > 5 ; 4 + 5 > 3 ; 3 5 > 4, ∴ Yes, a triangle can be formed with these sides.
ii) ∴Yes. A triangle can be formed with these sides.
iii) 4 + 4 > 8
∴ With these sides, a triangle cannot he formed.
iv) 3 + 5 > 7; 5 + 7 > 3; 3 + 7 > 5
∴ Yes. A triangle can he formed with these sides.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 2 Fractions, Decimals and Rational Numbers Ex 5 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 2nd Lesson Fractions, Decimals and Rational Numbers Exercise 5

Question 1.
Which one is greater?
(i) 0.7 or 0.07
(ii) 7 or 8.5
(iii) 1.47or 1.51
(iv) 6 or 0.66
1 cm = 10 mm
1 m = 100cm
1 km = 1000m
1kg =1000gm
Solution:
i) 0.7 or 0.07 = 0.7 is greater
ii) 7 or 8.5= 8.5 is greater
iii) 1.47 or 1.50 = 1.50 is greater
iv) 6 or 0.66 = 6 is greater

Question 2.
Express the following as rupees using decimals.
(i) 9 paise
(ii) 77 rupees 7 paise
(iii) 235 paise
Solution:
(i) 9 paise = \(\frac { 9 }{ 100 }\) = ₹ 0.09
(ii) 77 rupees 7 paise = 77 rupees \(\frac { 7 }{ 100 }\) rupees = ₹ 77.07
(iii) 235 paise = ₹ \(\frac{235}{100}\) = ₹ 2.35

Question 3.
(i) Express 10 cm in metre and kilometre.
(ii) Express 45 mm in centimeter, meter and kilometer.
Solution:
i) 10cm = \(\frac{10}{100}\) m = 0.1 m
1o cm = \(\frac{10}{100 \times 1000}\) km = 0.0001 km

ii) 45 mm = \(\frac{45}{10}\) cm = 4.5 cm
= \(\frac{4.5}{100}\) m = 0.045 m
= \(\frac{0.045}{1000}\) km = 0.000045 km

Question 4.
Express the following in kilograms.
(i) 190g
(ii) 247g
(iii) 44kg 80gm
Solution:
(i) 190g = \(\frac{190}{1000}\) = 0.190 kg
(ii) 247g = \(\frac{247}{1000}\) kg = 0.247 kg
(iii) 44kg 80gm = 44 kg \(\frac{80}{1000}\) kg = 44.080kg

Question 5.
Write the following decimal numbers in expanded form.
(i) 55.5
(ii) 5.55
(iii) 303.03
(iv) 30.303
(v) 1234.56
Solution:
(i) 55.5 = 10 × 5 + 1 × 5 × \(\frac{1}{10}\) × 5 = 50 + 5 + \(\frac{5}{10}\)
(ii) 5.55 = 1 × 5 + \(\frac{1}{10}\) × 5 + \(\frac{1}{100}\) × 5 = 5 + \(\frac{5}{10}+\frac{5}{100}\)
(iii) 303.03 = 100 × 3 + 1 × 3 + \(\frac{1}{100}\) × 3 = 300 + 3 + \(\frac{3}{100}\)
(iv) 30.303 = 10 × 3 + \(\frac{1}{10}\) x 3 + \(\frac{1}{1000}\) x 3 = 30 + \(\frac{3}{10}+\frac{3}{1000}\)
(v) 1234.56 = 1000 × 1 + 100 × 2 + 10 × 3 + 1 × 4 + \(\frac{1}{10}\) × 5 + \(\frac{1}{100}\) × 6 = 1000 + 200 + 30 + 4 + \(\frac{5}{10}+\frac{6}{100}\)

Question 6.
Write the place value of 3 in the following decimal numbers.
(i) 3.46
(ii) 32.46
(iii) 7.43
(iv) 90.30
(v) 794.037
Solution:
i) 3.46 – place value of 3 in 3.46 is 3 × 1 =-3
ii) 32.46- place value of 3 in 32.46 is 3 × 10 = 30
iii) 7.43- place value of 3 in 7.43 is 3 × \(\frac{1}{100}\) = 0.03
iv) 90.30- place value of 3 in 90.30 is 3 × \(\frac{1}{10}\) = 0.3
v) 794.037 – place value of 3 in 794.037 is 3 × \(\frac{1}{100}\) = 0.03

Question 7.
Aruna and Radha start their journey from two different places. A and E. Aruna chose the path from A to B then to km C, while Radha chose the path from E to D then to C. Find who traveled more and by how much?
Solution:
Distance covered by Aruna = AB + BC
= 9.50+2.40 = 11.90km
Distance covered by Rad ha = ED + DC
= 8.25 + 3.75 = 12 km
Radha travelled more by (12.00 – 11.90) = 0.10 km.

Question 8.
Upendra went to the market to buy vegetables. He brought 2 kg 250 gm tomatoes, 2 kg 500gm potatoes, 750gm lady fingers and 125 gm green chillies. How much weight did Upendra cany back to his house?

Upendra carried back a total weight of 5.625 kg

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 4 Lines and Angles Ex 7 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 4th Lesson Lines and Angles Exercise 7

Question 1.
Fill up the blanks
(i) The line which intersects two or more lines at distinct points is called __________
(ii) If the pair of alternate interior angles are equal then the lines are ______________
(iii) The sum of interior angles on the same side of the transversal are supplementary then the lines are ____________
(iv) If two lines intersect each other then the number of common points they have
Solution:
i) The line which intersects two or more lines at distinct points is called transversal.
ii) If the pairs of alternate interior angles are equal then the lines are parallel.
ii) The sum of interior angles on the same side of the transversal are supplementary then the lines are parallel.
iv) If two lines intersect each other then the number of common points they have Only one.

Question 2.
In the adjacent figure, the lines ‘P and ‘m’ are parallel and ‘n’ is a transversal. Fill in the blanks for all the situations given below.

(i) If ∠1 = 80° then∠2 =
(ii) If ∠3 = 45° then ∠7 =
(iii) If ∠2 = 90° then ∠8 =
(iv) If ∠4 = 100° then ∠8 =
Solution:
(i) If ∠1 = 80° then∠2 = 100
(ii) If ∠3 = 45° then ∠7 = 45
(iii) If ∠2 = 90° then ∠8 = 90
(iv) If ∠4 = 100° then ∠8 = 100

Question 3.
Find the measures of x,y and z in the figure, where l || BC

Solution:
∠y = 75° (alt. tnt. angles)
∠z = 45° (ait. tnt. angles)
∠x + ∠y + ∠z = 180° (∵ int. angles of a triangle = 1800)
75° + 45° + ∠x = 180°
∠x = 180°- 120°
= 60°

Question 4.
ABCD is a quadrilateral in which AB || DC and AD || BC. Find ∠b, ∠c and ∠d.
Solution:
∠b + ∠50° = 180° (int. angles on the same side of AB)
∠b = 180° – 50° = 130°
Similarly ∠b + ∠c = ∠c + ∠d = ∠d + ∠50 = 180°
∠130° + ∠c = 180°
∠c = 180° – 130° = 50°
Also ∠c + ∠d = 50° +∠d = 180°
∠d = 180° – 50° = 130°

Question 5.
In a given figure, ‘l’ and m’ are intersected by a transversal ‘n’. Is 1 || m?

Solution:
∠AQP and ∠CRS are exterior angles on the same side of the transversal n and their sum
100° + 80° = 180°
Hence l//m.

Question 6.
Find ∠a, ∠b, ∠c, ∠d and ∠e in the figure? Give reasons.

Note: Two anow marks pointing in the same direction represent parallel lines.
Solution:
∠a = ∠50° (∵ alt. int, angle between two parallel lines)
∠b = 50° (∵ alt. int, angle between two parallel lines)
∠b = ∠c = 50° (∵ alt. int. angles between two parallel lines)
∠c = ∠d = 50° ( ∵ alt. int angles between two parallel lines)
∠e = ∠d = 50°(∵ alt. int. angles between two parallel lines)

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 6 Ratio – Applications Ex 6 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 6th Lesson Ratio – Applications Exercise 6

Question 1.
How long will it take for a sum of ₹ 12600 invested at 9% per annum beocme to ₹ 15624?
Solution:
HereA = ₹ 15,624 R = 9% T = ?
P = ₹ 12,600
∴ I = A – P = 15,624 – 12,600 = ₹ 3024
Also I = \(\frac{P R T}{100}\)
∴ 3024 = \(\frac{12,600 \times 9 \times \mathrm{T}}{100}\)

Question 2.
At what rate a sum doubles itself in 8 year 4 months?
Solution:
Given that A = double the sum
Let the principle be P
then A = 2P
T =8 years 4 months = 8y \(\frac { 4 }{ 12 }\) y = 8\(\frac { 1 }{ 3 }\) years = \(\frac { 25 }{ 3 }\)
R = R% say
We know that
I = \(\frac{\text { PTR }}{100}\)
Here I = A – P
= 2P – P = P
∴ P = \(\frac{P \cdot \frac{25}{3} \times R}{100}\)
∴ R = 100 x \(\frac{3}{25}\) = 12%

Question 3.
A child friendly bank announces a savings scheme for school children. They will give kiddy banks to children. Children have to keep their savings in it and the bank collects all the money once in a year. To encourage children savings, they give 6% interest if the amount exceeds by ₹ 10000. and other wise 5%. Find the interest received by a school if they deposit is ₹ 9000 for one year.
Solution:
Money deposited = ₹ 9000
Interest applicable 5% on ₹ 9000
= 5 × \(\frac{9000}{100}\) = ₹ 450

Question 4.
A sum of money invested at 8% per annum for simple interest amounts to ₹ 12122 in 2 years. What will it amounts to in 2 year 8 months at 9% rate of interest?
Solution:
First part
Pirnciple = P say
R=8%
T = 2 years
A = ₹ 12,122

Second part
P = ₹10,450
R = 9%
T = 2 years 8 months, A = ?

Question 5.
In 4 years, ₹ 6500 amounts to ₹ 8840 at a certain rate of interest. In what time will ₹ 1600 amounts to 1816 at the same rate?
Solution:
First part
T = 4 years
P = ₹ 6500
A = ₹ 8840
R = R% = ?
I = A – P = 8840 – 6500 = ₹ 2340
But I = \(\frac{P T R}{100}\)
∴ 2340 = \(\frac{6500 \times 4 \times R}{100}\)
∴ R = \(\frac{2340 \times 10 \theta}{6500 \times 4}=\frac{36}{4}\) = 9%

Second part
P = ₹ 1600
A = ₹ 1816
T = ?
R = 9%
I = A – P = 1816 – 1600 = ₹ 216
But I = \(\frac{P T R}{100}\)
∴ 2340 = \(\frac{1600 \times T \times 9}{100}\)
∴ R = \(\frac{216 \times 100 \theta}{1600 \times 9}=\frac{3}{2}\) = 1 \(\frac { 1 }{ 2 }\) years.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 6 Ratio – Applications Ex 5 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 6th Lesson Ratio – Applications Exercise 5

Question 1.
A shopkeeper bought a suit case for ₹ 480 and sold it for ₹ 540. Find his gain percent?
Solution:
C.P of the suitcase = ₹ 480
SP of the suitcase = ₹ 540
∴ gain=S,P-C.P = 540 – 480 = ₹ 60
∴ gain percent = \(\frac { 60 }{ 450 }\) × 100% = 12.5%

Question 2.
Ajay bought a TV for ₹ 15000 and sold it for ₹141 00. Find the loss percent?
Solution:
C.P of the TV = ₹ 15,000
S.P of the TV = ₹ 14100
As S.P < C.P
Loss = C.P – S.P= 15,000 – 14,100 = ₹ 900
∴ Loss percent = \(\frac { 900 }{ 15000 }\) × 100 = 6%

Question 3.
Ramu sold a plot of land for ₹ 2,40,000 gaining 20%. For how much did he purchase the plot?
Solution:
Let the cost price of the land = ₹ x
gain percent = 20% of the C.P
∴ S.P of the land = 120% of C.P
By problem, 120% of x = 2,40,000
\(\frac { 120. x }{ 100 }\) = 2,40,000
x = 2.40000 × \(\frac {100 }{ 120 }\)
= ₹ 2,00,000

(OR)

Let the C.P of the land = ₹ x
gain percent = 20% of C.P = 20% of x = \(\frac{20 \mathrm{x}}{100}\)
∴ S.P of the land = C.P + gain
= x + \(\frac{20 \mathrm{x}}{100}\)
= \(\frac{100 x+20 x}{100}=\frac{120 x}{100}\)

By problem, \(\frac{20 \mathrm{x}}{100}\) = 2,40.000
∴ x = 24000 x \(\frac { 100 }{ 120 }\)
= ₹ 2,00,000

Question 4.
On selling a mobile for ₹ 750, a shop keeper looses 10%. For what amount should he sell it to gain 5%?
Solution:
Let the C.P of the mobile be x
Losspercent = 10% of C.P = 10% of x = \(\frac{10 \mathrm{x}}{100}\)
∴ Loss = \(\frac{10 x}{100}\)
∴ S.P = C.P – Loss
= \(x – \frac{10 x}{100}=\frac{100 x-10 x}{100}=\frac{90 x}{100}\)

By problem, \(\frac{90 \mathrm{x}}{100}\) = 750
x = 750 × \(\frac { 100 }{ 90 }\) = ₹ \(\frac { 2500 }{ 3 }\)
Now to gain by 5% the S.P = C.P + 5% of C.P

Question 5.
A farmer sold 2 bullocks for ₹ 24000 each. On one bullock he gained 25% and on the other he lost 20%. Find his total profit or loss percent?
Solution:
Let the C.P of first bullock be x
gain = 25% of x = 25 × \(\frac{x}{100}=\frac{25 x}{100}\)
S.P = C.P + gain = x + \(\frac{25 x}{100}=\frac{100 x+25 x}{100}=\frac{125 x}{100}\)
Selling price of first bullock 24,000 (given)
\(\frac{125 x}{100}\) = 24000
x = \(\frac{24000}{125}\) × 100
∴ C.P of first bullock = ₹ 19.200
Let the C.P of second bullock be y
Loss percent = 20%

∴Loss = \(\frac{20 \times \mathrm{y}}{100}=\frac{20 \mathrm{y}}{100}\)

S.P = C.P – loss
= \(y-\frac{20 y}{100}=\frac{100 y-20 y}{100}=\frac{80 y}{100}\)

But S.P = ₹ 24,000 (given)
\(\frac{80 \mathrm{y}}{100}\) = 24,000
∴ y = 24000 x \(\frac{100}{80}\) = 30,000

∴ C.P of second bullock = ₹ 30,000
C.P of 2 bullocks = ₹19,200 + ₹30,000
= ₹ 49,200
S.P of 2 bullocks ₹24,000 × 2 = ₹48,000
Loss = C.P – S.P = 49,200 – 48,000 = ₹1200
Loss % = \(\frac{\text { loss }}{\text { CP }}\) × 100
= \(\frac{1200}{49200}\) × 100 = 2.4
∴ Loss% = 2.4%

Question 6.
Sravya bought a watch for ₹480. She sold it to Ridhi at a gain of 6\(\frac { 1 }{ 4 }\) %. Ridhi sold it to Divya at a gain of 10%. How much did Divya pay for it?
Solution:
CF of the watch = ₹ 480
Gain% = \(6 \frac{1}{4} \%=\frac{25}{4} \%\)
Gain = 480 × \(\frac{25}{4}\) x \(\frac{1}{100}\) = 30
C.P of the watch for Ridhi = 480 + 30 = ₹ 510
Gain% = 10%
∴ Gain= 51% × \(\frac{10}{100}\) = 51
S.P of the watch for Ridhi = 510 + 51 = ₹561
∴ Amount paid for Divya for the watch = ₹561

Question 7.
The marked price of a book is ₹225.Thc publisher allows a discount of ₹10% on it. Find the selling price of it?
Solution:
The marked price of the book = ₹ 225
Discount 10%
∴ Discount = 225 × \(\frac{10}{100}\)= ₹ 22.5
S.P = M.P – discount
= 225 – 22.5 = ₹202.5
∴ Selling price of the book = ₹ 202.5

Question 8.
A carpenter allows 15% discount on his goods. Find the marked price of a chair which is sold by him for ₹680?
Solution:
Let the marked price of chair be ₹x
Discount = 15% = x × \(\frac{15}{100}=\frac{15 x}{100}\)
S.P = M.P – discount
\(x-\frac{15 x}{100}=\frac{100 x-15 x}{100}=\frac{85 x}{100}\)
S.P = ₹ 680 (given)
∴ \(\frac{85 \mathrm{x}}{100}\) = 680
x = \(\frac{680 \times 100}{85}\) = 800
Marked price of the chair = ₹ 800

Question 9.
A dealer allows a discount of ₹ 10% and still gains by 10%. What should be the marked price if the cost price is ₹900?
Solution:
Given that C.P = 900
There is a gain of 10% on C.P
∴ Gain = 10% of ₹ 900
= \(\frac{10 \times 900}{100}\) = ₹ 90
∴ S.P = C.P . gain
= 900 + 90
S.P = ₹990 …………….. (1)
Let the marked price = ₹ x
Discount on it = 10% on M.P = \(\frac{10 \mathrm{x}}{100}\)
∴ Selling Price = MP – Discount
= x – \(\frac{10 \mathrm{x}}{100}\)
= \(\frac{100 x-10 x}{100}\)
∴ S.P = \(\frac{90 \mathrm{x}}{100}\) …………….(2)
From (1) & (2) \(\frac{90 \mathrm{x}}{100}\) = 990
∴ x = 990 x \(\frac{100}{90}\)
∴ M.P = x = ₹1100

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 4 Lines and Angles Ex 6 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 4th Lesson Lines and Angles Exercise 6

Question 1.
Name two pairs of vertically opposite angles in the figure.

Solution:
Vertically opposite angles are
∠AOC, ∠BOD and ∠BOC, ∠AOD

Question 2.
Find the measure of x, y and z without actually measuring them.

Solution:
From the figure
∠y and 160° are vertically opposite angles and hence equal.
∴ ∠y=1600
Also ∠x = ∠z and (. vertically opposite angles)
x + 160° = 180° (Linear pair of angles)
∴ ∠x = 180° – 160° = 20°
∠z = 20° (∵ ∠x, ∠z are vertically opposite)
∴ x = 20°
y = 160°
z = 20°

Question 3.
Give some examples of vertically opposite angles in your surroundings.
Solution:
i) Angles between legs of a folding cot/scamp cot.
ii) Angles between legs of a folding chair.
iii) Angles between plates of a scissors.