AP 10th Class Maths Important Questions Chapter 11 త్రికోణమితి

These AP 10th Class Maths Chapter Wise Important Questions 11th Lesson త్రికోణమితి will help students prepare well for the exams

AP Board 10th Class Maths 11th Lesson Important Questions and Answers త్రికోణమితి

ప్రశ్న 1.
sin A = cos A అయిన A విలువను డిగ్రీలలో తెల్పండి.
సాధన.
sin A = cos A
⇒ sin A = sin (90 – A) (∵ A = 90 – A)
⇒ 2A = 90
⇒ A = \(\frac{90}{2}\) = 45°

ప్రశ్న 2.
2 sin x = √3 అయినచో x విలువెంత?
సాధన.
2 sin x = √3
⇒ sin x = \(\frac{\sqrt{3}}{2}\)
sin x = sin 60°
⇒ x = 60°.

ప్రశ్న 3.
గణించుము:
(i) cos 76° – sin 14°
(ii) \(\frac{\tan 73^{\circ}}{\cot 17^{\circ}}\)
సాధన.
(i) cos 76° – sin 14° = cos (90 – 14) – sin 14
= sin 14° – sin 14° (∵ cos (90 – θ) = sin θ)
= 0
∴ cos 76° – sin 14° = 0 ………….(i)

(i) \(\frac{\tan 73^{\circ}}{\cot 17^{\circ}}\) = \(\frac{\tan (90-17)}{\cot 17}=\frac{\cot 17^{\circ}}{\cot 17^{\circ}}\)
= 1
∴ \(\frac{\tan 73^{\circ}}{\cot 17^{\circ}}\) = 1

ప్రశ్న 4.
tan² 45° + cot² 30° విలువను కనుక్కోండి.
సాధన.
tan 45° + cot² 30°
= (1)² + (√3)²
= 1 + 3 = 4.

ప్రశ్న 5.
sin² 30° + cos² 60° విలువను కనుగొనుము.
సాధన.
sin 30° = \(\frac{1}{2}\), cos 60° = \(\frac{1}{2}\)
sin² 30° + cos² 60° = (\(\frac{1}{2}\))² + (\(\frac{1}{2}\))²
= \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)
∴ sin² 30° + cos² 60° = \(\frac{1}{2}\)

ప్రశ్న 6.
sin (A + B) = 1 మరియు cos B = \(\frac{1}{2}\) ∠A, ∠Bలను కనుగొనుము. (0°< A + B ≤ 90°)
సాధన.
sin (A + B) = 1
sin (A + B) = sin 90°
A + B = 90°
cos B = \(\frac{1}{2}\)
cos B = cos 60°
∴ ∠B = 60°
∴ ∠A = 90° – 60° = 30°.

ప్రశ్న 7.
cot² θ – \(\frac{1}{\sin ^{2} \theta}\) ను సూక్ష్మీకరించండి.
సాధన.
\(\frac{\cos ^{2} \theta}{\sin ^{2} \theta}-\frac{1}{\sin ^{2} \theta}=\frac{\cos ^{2} \theta-1}{\sin ^{2} \theta}=\frac{\sin ^{2} \theta}{\sin ^{2} \theta}\) = 1

ప్రశ్న 8.
‘θ’ ఏదేని అల్పకోణమైతే sin θ = \(\frac{5}{3}\); వ్యవస్థితమగునా? .. కారణం తెలపండి.
సాధన.
‘θ’ అల్పకోణము = 0° < θ < 90°
కనుక sin 0° = 0 మరియు sin 90° = 1
కనుక 0° < θ < 90°కు sin θ విలువ 0 మరియు 1ల మధ్య ఉంటుంది.
కనుక sin θ విలువ 1 కంటే ఎక్కువ ఉండదు.
∴ sin θ = \(\frac{5}{3}\) వ్యవస్థతము కాదు.

ప్రశ్న 9.
sin x = \(\frac{3}{4}\) అయితే cosec x విలువ కనుగొనుము.
సాధన.
sin x = \(\frac{3}{4}\) అయితే
cosec x = \(\frac{1}{\sin x}=\frac{1}{\frac{3}{4}}=\frac{4}{3}\)

ప్రశ్న 10.
sin 90°, cos 90°, tan 90°, cot 90°, sec 90° మరియు cosec 90° లలో ఏది( వి) నిర్వహించబడదు?
సాధన.
sin 90° = 1
cos 90° = 0
tan 90° = నిర్వహించబడదు
cot 90° = 0
sec 90° = నిర్వహించబడదు
cosec 90° = 1
∴ tan 90°, sec 90° లు నిర్వహించబడవు.

ప్రశ్న 11.
(sec² x – 1) (cot² x) ను సూక్ష్మ రూపంలో తెల్పండి.
సాధన.
(sec² x – 1) (cot² x) = (tan² x) (cot² x) [∵ sec²A – tan² A = 1]
= \(\frac{\sin ^{2} x}{\cos ^{2} x} \cdot \frac{\cos ^{2} x}{\sin ^{2} x}\)[tan A = \(\frac{\sin A}{\cos A}\), cot A = \(\frac{\cos A}{\sin A}\)]
= 1.

ప్రశ్న 12.
tan (A – B) = \(\frac{1}{\sqrt{3}}\) మరియు sin A = \(\frac{\sqrt{3}}{2}\) అయినచో ∠B మరియు cos B ల విలువలు కనుగొనండి (A, B < 90°)
సాధన.
tan (A – B) = \(\frac{1}{\sqrt{3}}\)
∴ tan (A – B) = tan 30°
∴ A – B = 30°
sin A = \(\frac{\sqrt{3}}{2}\)
sin A = sin 60°
∴ A = 60° ప్రతిక్షేపించిన
A – B = 30°
⇒ 60° – B = 30°
⇒ B = 30°
⇒ cos B = cos 30°
⇒ cos B = \(\frac{\sqrt{3}}{2}\)

ప్రశ్న 13.
tan A = \(\frac{1}{\sqrt{3}}\) మరియు tan B = √3 అయిన sin A . cos B + cos A . sin B విలువను కనుగొనుము (A, B < 90°)
సాధన.
tan A = \(\frac{1}{\sqrt{3}}\) మరియు tan B = √3 (A, B < 90°)
∴ tan A = \(\frac{1}{\sqrt{3}}\) = tan 30° (∵ A < 90°)
⇒ A = 30° మరియు tan B = √3 = tan 60° ⇒ B = 60°
(∵ AB < 90°)
⇒ A = 30°, B = 60° అయిన
sin A cos B + cos A sin B విలువ = sin 30° cos 60° + cos 30° sin 60°
∴ sin 30° cos 60° + cos 30° sin 60° = \(\frac{1}{2} \cdot \frac{1}{2}+\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2}\)
= \(\frac{1}{4}+\frac{3}{4}=\frac{4}{4}\)
= 1

IInd method :
sin A cos B + cos A sin. B = sin (A + B) నందు
A = 30°, B = 60° ప్రతిక్షేపించిన
sin (A + B) = sin (30° + 60°)
= sin 90° = 1.

ప్రశ్న 14.
tan² A – sin² A = tan² A . sin² A అని చూపండి.
సాధన.
tan² A – sin² A = \(\frac{\sin ^{2} A}{\cos ^{2} A}\) – sin² A
= sin² A (\(\frac{1}{\cos ^{2} A}\) – 1)
= sin² A (sec² A – 1)
= sin² A. tan² A

ప్రశ్న 15.
cos A = \(\frac{7}{25}\) అయిన sin A మరియు cosec A లను కనుగొనండి. నీవేమి గమనించితివి ?
సాధన.

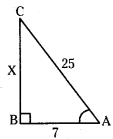
∆ABC లంబకోణ త్రిభుజరీలో
cos A = \(\frac{7}{25}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
x² + 7² = 25²
x² = 25² – 7² = 576
x = 24
sin A = \(\frac{24}{25}\) cosec A = \(\frac{25}{24}\)
cosec A = \(\frac{1}{\sin A}\) అని పరిశీలించితిని.

ప్రశ్న 16.
tan 2A = cot (A – 18°), 2A ఒక అల్పకోణము అయితే A యొక్క విలువను కనుగొనుము.
సాధన.
tan 2A = cot(A – 18°)
= cot[90 – (90 – (A – 18°)]]
tan 2A = tan [90 – (A – 18°)]
2A = 90 – (A – 18°)
= 90 – A + 18°
⇒ 3A = 108°
∴ A = 36°

ప్రశ్న 17.
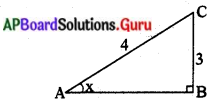
4 tan θ = 3 అయిన sec e మరియు cosec 2ల విలువలు కనుగొనుము.
సాధన.
4 tan θ = 3
⇒ tan θ = \(\frac{3}{4}\)

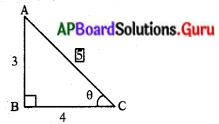
AC = \(\sqrt{\mathrm{BC}^{2}+\mathrm{AB}^{2}}\)
= \(\sqrt{4^{2}+3^{2}}\) = 5
sec θ = \(\frac{5}{4}\); cosec θ = \(\frac{5}{3}\).

ప్రశ్న 18.
tan 2A = cot (A – 27), 2A అల్పకోణమైన A విలువ కనుగొనండి.
సాధన.
దత్తాంశం ప్రకారం, 2A అల్పకోణము
tan 2A = cot (A – 27)
⇒ 2A + A – 27 = 90
⇒ 2A + A = 90 + 27 (∵ tan (90 – θ) = cot θ)
⇒ 3A = 117
⇒ A = \(\frac{117}{3}\) = 39
∴ A = 39°

ప్రశ్న 19.
\(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A అని చూపండి.
సాధన.
\(\sqrt{\frac{1+\sin A}{1-\sin A}}\)
(లవ, హారాలను \(\sqrt{1+\sin A}\) తో గుణించిన)

ప్రశ్న 20.
(sin x – cos x)² + (sin x + cos x)² విలువ కనుగొనండి.
సాధన.
(sin x – cos x)² + (sin x + cos x)² = sin² x + cos² x – 2 sin x cos x + sin² x + cos² x + 2 sin x cos x
= 2(sin² x + cos² x) = 2(1) = 2

ప్రశ్న 21.
cos A = \(\frac{12}{13}\) అయితే sin A మరియు tan A విలువను కనుగొనండి.
సాధన.

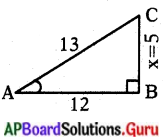
AC² = AB² + BC²
13² = 12² + x²
169 = 144 + x²
x² = 25
⇒ x = 5
sin A = \(\frac{5}{13}\)
tan A = \(\frac{\sin A}{\cos A}=\frac{\frac{5}{13}}{\frac{12}{13}}=\frac{5}{13} \times \frac{13}{12}=\frac{5}{12}\)
∴ sin A = \(\frac{5}{13}\), tan A = \(\frac{5}{12}\).

ప్రశ్న 22.
4 sin² θ – 1 = 0 అయిన (θ < 90) θ విలువ కనుగొని cos² θ + tan² θ విలువను కనుగొనండి
సాధన.
4 sin² θ – 1 = 0
⇒ 4 sin² θ = 1
sin² θ = \(\frac{1}{4}\)
⇒ sin θ = ± \(\sqrt{\frac{1}{4}}\)
= ± \(\frac{1}{2}\)
θ < 90°. అని ఇవ్వబడింది
కాబట్టి sin θ = \(\frac{1}{2}\)
∴ θ = 30°
cos θ = cos 30° = \(\frac{\sqrt{3}}{2}\)
tan θ = tan 30° = \(\frac{1}{\sqrt{3}}\)
cos² θ + tan² θ = \(\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}\)
= \(\frac{3}{4}+\frac{1}{3}=\frac{9+4}{12}=\frac{13}{12}\)

ప్రశ్న 23.
(sin θ – cosec θ)² + (cos θ – sec θ)² = cot θ + tan² θ – 1 అని నిరూపించండి.
సాధన.
(sin θ – cosec θ)² + (cos θ – sec θ)² = sin² θ + cosec² θ – 2 sin θ . cosec θ + cos² θ + sec² θ – 2 cos θ · sec θ
= (sin² θ + cos² θ) + cosec² θ + sec² θ – 2 – 2
= 1 + (1 + cot² θ) + (1 + tan² θ) – 2 – 2
= cot² θ + tan² θ + 3 – 4
= cot² θ + tan ² θ – 1.

ప్రశ్న 24.
cosec θ + cot θ = p అయితే \(\frac{p^{2}+1}{p^{2}-1}\) = sec θ అని చూపండి.
సాధన.
cosec θ + cot θ = p.
∴ cosec θ – cot θ = \(\frac{1}{p}\)
cosec θ + cot θ = p
2 cosec θ = p + \(\frac{1}{p}\)
cosec θ – cot θ = \(\frac{1}{p}\)
2 cot θ = p – \(\frac{1}{p}\)
= \(\frac{p^{2}-1}{p}\)
\(\frac{\frac{p^{2}+1}{p}}{\frac{p^{2}-1}{p}}=\frac{2 \cosec \theta}{2 \cot \theta}\)

\(\frac{\mathrm{p}^{2}+1}{\mathrm{p}^{2}-1}=\frac{\frac{1}{\sin \theta}}{\frac{\cos \theta}{\sin \theta}}=\frac{1}{\cos \theta}\) = sec θ.

ప్రశ్న 25.
sec θ + tan θ = p. అయిన sin θ = \(\frac{p^{2}-1}{p^{2}+1}\) అని నిరూపించండి.
సాధన.
sec θ + tan θ = p
sec² θ – tan² θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
p. (sec θ – tan θ) = 1

ప్రశ్న 26.
cot θ = \(\frac{7}{8}\) అయిన
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) \(\frac{1+\cos \theta}{\sin \theta}\) విలువలు కనుగొన౦డి.
సాధన.
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\) = \(\frac{1-\sin ^{2} \theta}{1-\cos ^{2} \theta}=\frac{\cos ^{2} \theta}{\sin ^{2} \theta}\)
= cot² θ.
= \(\left(\frac{7}{8}\right)^{2}=\frac{49}{64}\) → (1)
(∵ sin² θ + cos² θ = 1)

(ii) \(\frac{1+\cos \theta}{\sin \theta}\) = \(\frac{1}{\sin \theta}+\frac{\cos \theta}{\sin \theta}\)
= cosec θ + cot θ
cot θ = \(\frac{7}{8}\) కావున, (1 + cot² θ) = cosec² θ
⇒ 1 + (\(\frac{7}{8}\))² = cosec² θ
⇒ 1 + \(\frac{49}{64}\) = \(\frac{64+49}{64}=\frac{113}{64}\)
∴ cosec θ = \(\sqrt{\frac{113}{64}}\)
∴ \(\frac{1+\cos \theta}{\sin \theta}\) = cosec θ + cot θ
= \(\frac{\sqrt{113}}{8}+\frac{7}{8}=\frac{7+\sqrt{113}}{8}\).

ప్రశ్న 27.
sec² θ + cosec² θ = sec² θ . cosec² θ .
సాధన.
sec² θ + cosec² θ = \(\frac{1}{\cos ^{2} \theta}+\frac{1}{\sin ^{2} \theta}\)
= \(\frac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin ^{2} \theta \cdot \cos ^{2} \theta}\)

= \(\frac{1}{\sin ^{2} \theta \cdot \cos ^{2} \theta}\)

= \(\frac{1}{\sin ^{2} \theta} \cdot \frac{1}{\cos ^{2} \theta}\)

= cosec² θ . sec² θ