AP 10th Class Maths Important Questions Chapter 12 త్రికోణమితి అనువర్తనాలు

These AP 10th Class Maths Chapter Wise Important Questions 12th Lesson త్రికోణమితి అనువర్తనాలు will help students prepare well for the exams

AP Board 10th Class Maths 12th Lesson Important Questions and Answers త్రికోణమితి అనువర్తనాలు

ప్రశ్న 1.
ఒక బాలుడు విద్యుత్ స్తంభం అడుగు భాగం నుండి 10 మీ. దూరంలో ఉన్న బిందువు నుండి విద్యుత్ 2. స్తంభం పై భాగాన్ని 30° ఊర్ధ్వకోణంతో పరిశీలించాడు. ఈ సందర్భానికి సరిపడు పటాన్ని గీయండి.
సాధన.

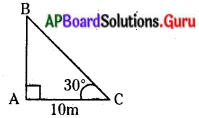
AB = విద్యుత్ స్తంభం ఎత్తు
AC = విద్యుత్ స్తంభం
అడుగు భాగం నుండి పరిశీలకునికి గల దూరం = 10 మీ.
ఊర్థ్వకోణం = 30°.

ప్రశ్న 2.
క్రింది సన్నివేశంలో గాలిపటం ఎత్తు కనుగొనుటకు తగిన పటాన్ని గీయండి. “ఒక వ్యక్తి ‘I’ పొడవు గల దారంతో కూడిన గాలిపటాన్ని ‘d ఊర్ధ్వకోణంతో ఎగుర వేయుచున్నాడు”.
సాధన.

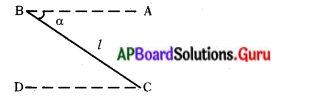
‘B’ వద్ద గాలిపటం ఉంది.
BC = దారం పొడవు = ‘l’

ప్రశ్న 3.
ఒక టవర్ ఎత్తు 100√3 మీటర్లు. దాని పాదం నుండి 100 మీటర్ల దూరంలో గల ఒక బిందువు నుండి ఆ టవర్ పై భాగాన్ని చూడాలంటే ఎంత ఊర్థ్వ కోణంతో చూడాలో కనుగొనండి.
సాధన.

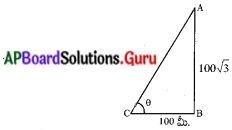
టవర్ ఎత్తు AB = 100√3 మీ.
టవర్ అడుగు భాగం నుండి పరిశీలకునికి గల దూరం BC = 100 మీ.
∆ABC లో tan θ = \(\frac{100 \sqrt{3}}{100}\) = √3
= tan 60°
⇒ θ = 60°.

ప్రశ్న 4.
రెహమాన్ ఒక గుడి గోపురం అడుగు భాగం నుండి 24 మీ. దూరంలో గల పరిశీలక స్థానం నుండి గోపుర శిఖరాన్ని 30° ఊర్ద్వకోణంతో పరిశీలించిన ఆ గోపురం ఎతును కనుక్కోండి.
సాధన.

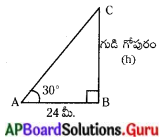
పరిశీలకునికి, గుడి గోపురం అడుగుభాగానికి మధ్య గల దూరం = 24 మీ.
గుడి గోపురం ఎత్తు = h మీ. .
θ = 30°
∆ABC నుండి
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{24}\)
⇒ h = \(\frac{24}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\) = 8√3 మీ…
గుడి గోపురం ఎత్తు = 8√3.మీ.

ప్రశ్న 5.
1.8 మీ. ఎత్తు కల్గిన ‘ఒక పరిశీలకుడు 13.2 మీ. దూరంలో గల చెట్టు పైభాగాన్ని తన కంటి నుండి 45° ఊర్ధ్వకోణంతో పరిశీలిస్తున్నాడు. అయిన ఆ తాటిచెట్టు ఎత్తు ఎంత ?
సాధన.
పరిశీలకుని ఎత్తు = 1.8 మీ. = AB
చెట్టు నుండి దూరము = 13.2 మీ. = AE = BD
ఊర్థ్వకోణము = ∠CBD = 45°

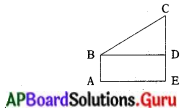
∆ BCD లో tan 45° = \(\frac{C D}{B D}\)
⇒ 1 = \(\frac{\mathrm{CD}}{13.2}\)
CD = 13.2 మీ.
∴ తాటిచెట్టు ఎత్తు = CE
= CD + DE
= 13.2 మీ. + 1.8 = 15 మీ.

ప్రశ్న 6.
7 మీ. పొడవుగల ఒక జెండా స్థంభము 8మీ. పొడవు గల నీడను ఏర్పరుచును. అదే సమయములో దగ్గరలో గల ఒక భవనము 32 మీ. పొడవు గల నీడను ఏర్పరచిన ఆ భవనము ఎత్తు ఎంత ?
సాధన.

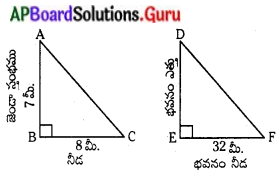
∆ABC ~ ∆DEF;
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}\)
\(\frac{7}{\mathrm{DE}}=\frac{8}{32}\)
∴ DE = 28 మీ.

ప్రశ్న 7.
6 మీ. మరియు 11 మీ. పొడవు గల స్తంభాలు ఒక చదునైన నేలపై కలవు. నేలపై ఆ రెండు స్తంభాల అడుగు భాగాల మధ్య దూరము 12 మీ. అయిన ఆ రెండు స్తంభాల పైభాగముల మధ్య దూరం ఎంత ?
సాధన.
దత్తాంశం ప్రకారం,
మొదటి స్తంభము పొడవు = AB = 6 మీ.
రెండవ స్తంభము పొడవు = CD = 11 మీ.

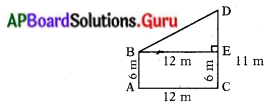
రెండు స్తంభాల అడుగు భాగాల మధ్య దూరము = AC = 12 మీ.
రెండు స్తంభాల పైభాగముల మధ్యదూరము = BD
పటం ప్రకారం,
BE = AC = 12 మీ.;
AB = EC = 6 మీ.
∴ DE = DC – EC
= 11 – 6 = 5 మీ.
BD² = DE² + BE²
= 5² + 12²
= 25 + 144 = 169
∴ BD = √169 = 13 మీ.

ప్రశ్న 8.
900 మీ. ఎత్తులో ఎగురుతున్న విమానం నుండి ఒక పరిశీలకుడు అతనికి ముందు వైపు అదే రేఖలో రెండు నావలను 60° మరియు 30° నిమ్నకోణాలతో గమనించిన ఆ రెండు నావల మధ్య దూరమెంత ?
సాధన.

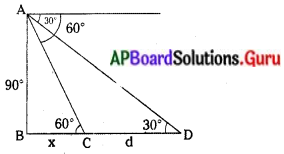
∆ABC లో tan 60 = \(\frac{900}{x}\)
√3 = \(\frac{900}{x}\)
⇒ x = \(\frac{900}{\sqrt{3}}\) = 300√3
∆ABD లో tan 30 = \(\frac{900}{x+d}\)
\(\frac{1}{\sqrt{3}}=\frac{900}{300 \sqrt{3}+d}\)
d = 600√3 మీ.

ప్రశ్న 9.
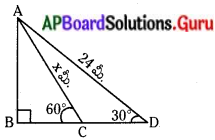
భూమితో 30°ల ఊర్ధ్వ కోణము చేస్తూ 24 మీటర్ల పొడవున్న ఒక దృఢమైన లోహపు తీగ ఆధారంగా ఒక విద్యుత్ స్థంభము నిలబెట్టబడి ఉంది. తీగ పొడవు చాలా ఎక్కువ ఉన్న కారణంగా తీగలో కొంత భాగము కత్తిరించి, మిగిలిన దానిని భూమితో 60° కోణము చేస్తూ అమర్చబడినది. అయిన కత్తిరించిన తీగ పొడవు ఎంత?
సాధన.
కత్తిరించకముందు లోహపు తీగ పొడవు (AD) = 24 మీ.
కత్తిరించిన తదుపరి లోహపు తీగ పొడవు (AC) = x మీ.
కరెంటు స్తంభము ఎత్తు = AB
ఊర్వకోణము ∠BDA = 30°; ∠BCA = 60°
లంబకోణ త్రిభుజము ABD నుండి

sin 30° = \(\frac{\mathrm{AB}}{\mathrm{AD}}\)
\(\frac{1}{2}=\frac{\mathrm{AB}}{24}\)
2AB = 24
AB = 12 మీ.
లంబకోణ త్రిభుజము ABC నుండి
sin 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{12}{\mathrm{AC}}\)
√3 AC = 24
⇒AC = \(\frac{24}{\sqrt{3}}\) = 8√3 మీ.
= 8 × 1.732 = 13.856 మీ.
కత్తిరించిన తీగ పొడవు = 24 – 13.856 = 10.144 మీ.

ప్రశ్న 10.
ఒక వ్యక్తి నిలువాటి టవర్ పై భాగం నుండి సమవేగంతో తనవైపు వస్తున్న కారును 30° నిమ్నకోణంతో పరిశీలిస్తున్నాడు. 12 సెకండ్ల తర్వాత నిమ్నకోణం 30° నుండి 60° కు మారిన ఆ స్థానం నుండి పరిశీలక స్థానం చేరుటకు ఎంతకాలం పట్టును ?
సాధన.
పటం నుండి,
సెకండ్లలో కారు ప్రయాణించిన దూరం = AB = x మీటర్లు
టవర్ ఎత్తు CD = h మీటర్లు

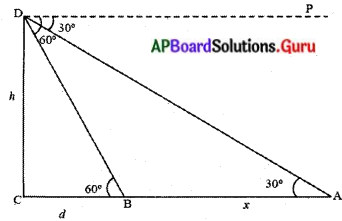
కారు ప్రయాణించాల్సిన మిగిలిన దూరం BC = d మీటర్లు
AC = AB + BC = (x + d) మీటర్లు
∠PDA = ∠DAC = 30°
∠PDB = ∠DBC = 60°
∆BCD నుండి, tan 60° = \(\frac{C D}{B C}\)
√3 = \(\frac{h}{d}\)
⇒ h = √3d ………… (1)
∆ACD నుండి,
tan 30° = \(\frac{C D}{A C}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{(x+d)}\)
⇒ h = \(\frac{(\mathrm{x}+\mathrm{d})}{\sqrt{3}}\) …………… (2)
(1) మరియు (2)ల నుండి,
\(\frac{(\mathrm{x}+\mathrm{d})}{\sqrt{3}}\) = √3d
⇒ x + d = 3d
⇒ x = 2d
⇒ d = A
‘x’ మీటర్ల దూరం ప్రయాణించడానికి పట్టు కాలం = 12 సెకండ్లు
‘d’ = \(\frac{x}{2}\) మీటర్ల దూరం ప్రయాణించడానికి పట్టు – కాలం = 6 సెకండ్లు.

ప్రశ్న 11.
60 మీటర్ల ఎత్తు గల ఒక గుడి పైభాగాన్ని దానికి ఇరువైపులా గల ఇద్దరు బాలురు 60° మరియు 30° ఊర్ధ్వకోణాలతో గమనిస్తే ఆ బాలురు మధ్య గల దూరాన్ని కనుగొనంది.
సాధన.
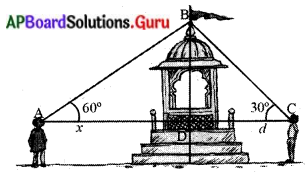
పటము నుండి దేవాలయం ఎత్తు BD = 60 మీటర్లు
మొదటి బాలుడు పరిశీలిస్తున్నపుడు ఊర్ధ్వకోణం ∠BAD = 60°
రెండవ బాలుడు పరిశీలిస్తున్నపుడు ఊర్థ్వకోణం ∠BCD = 30°
మొదటి బాలుడు నుండి గుడి దూరం AD = x,
రెండవ బాలుడు నుండి గుడి దూరం CD = d అనుకొనగా

∆BAD నుండి ∆BCD నుండి
tan 60° = \(\frac{\mathrm{BD}}{\mathrm{AD}}\)
√3 = \(\frac{60}{x}\)
x = \(\frac{60}{\sqrt{3}}\) …………..(1)

tan 30° = \(\frac{\mathrm{BD}}{\mathrm{d}}\)
\(\frac{1}{\sqrt{3}}=\frac{60}{d}\)
d = 60√3 ……………. (2)
(1) మరియు (2) ల నుండి ఇద్దరు వ్యక్తుల మధ్య దూరం
= AD + AC = x + d
= \(\frac{60}{\sqrt{3}}\) + 60√3
= \(\frac{60+180}{\sqrt{3}}\)
= \(\frac{240}{\sqrt{3}}\)
= 80√3 మీటర్లు.