These AP 10th Class Maths Chapter Wise Important Questions 8th Lesson సరూప త్రిభుజాలు will help students prepare well for the exams.
AP Board 10th Class Maths 8th Lesson Important Questions and Answers సరూప త్రిభుజాలు
ప్రశ్న 1.
ఒక చతురస్రం దీర్ఘ చతురస్రానికి సరూపాలా ? సమర్థించండి.
సాధన.
ఒక చదరము మరియు ఒక దీర్ఘచతురస్రమునందు అనురూపకోణాలు సమానముగా ఉండును. కాని అనురూప భుజాలు అనుపాతములో ఉండవు.

∴ ఒక చదరము మరియు ఒక దీర్ఘచతురస్రములు సరూపములు కావు.
ప్రశ్న 2.
∆ABC లో LM//BC మరియు \(\frac{A L}{L B}=\frac{2}{3}\) AM = 5 సెం.మీ. అయిన AC ఎంత?
సాధన.
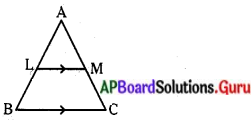
\(\frac{\mathrm{AL}}{\mathrm{LB}}=\frac{\mathrm{AM}}{\mathrm{MC}}\)
\(\frac{2}{3}=\frac{5}{M C}\)
MC = \(\frac{15}{2}\) = 7.5 సెం.మీ.
AC = AM + MC = 5 + 7.5 = 12.5 సెం.మీ.
![]()
ప్రశ్న 3.
∆ABC త్రిభుజములో DE || BC మరియు AC = 5.6 సెం.మీ., AE = 2.1 సెం.మీ. అయిన AD : DB ను కనుగొనుము. June 2018
సాధన.
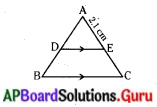
∆ABC లో DE || BC,
AE = 2.1 సెం.మీ.
EC = AC – AE
= 5.6 – 2.1 BL
= 3.5 సెం.మీ.
ప్రాథమిక అనుపాత సిద్ధాంతం ప్రకారం AD : DB = AE : EC
= 2.1 : 3.5 = 3 : 5
ప్రశ్న 4.
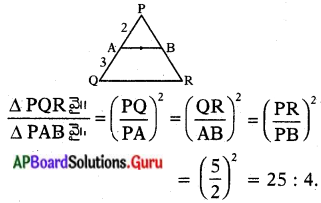
ఇవ్వబడిన పటంలో \(\overline{\mathbf{A B}}\) || \(\overline{\mathbf{Q R}}\) మరియు PA= 2 సెం.మీ., AQ = 3 సెం.మీ. అయిన ∆POR మరియు ∆PAB ల యొక్క వైశాల్యాల నిష్పత్తి కనుగొనండి.
సాధన.

దత్తాంశము AB || QR; PA = 2, AQ = 3
∆POR ~ ∆PAB
∴ PQ = 2 + 3 = 5
∴ సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి, వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము.
![]()
ప్రశ్న 5.
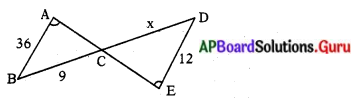
పై పటంలో ∠BAC = ∠CED అయితే ‘x’ యొక్క విలువ 3 అగునో, కాదో సరిచూడుము.
సాధన.
దత్తాంశం ప్రకారం, ∆ABC మరియు ∆ECD లో
∠A = ∠E
∠ACB = ∠ECD [∵ శీర్షాభిముఖ కోణాలు)
∴ ∠B = ∠D[∵ ఉమ్మడి కోణం ]
∴ ∆ABC ~ ∆EDC
⇒ \(\frac{A B}{E D}=\frac{B C}{D C}=\frac{A C}{E C}\)
⇒ \(\frac{36}{12}=\frac{9}{x}\)
⇒ 36x = 108
⇒ x = \(\frac{108}{36}\) = 3.
![]()
ప్రశ్న 6.
7.2 సెం.మీ. పొడవు గల ఒక రేఖాఖండమును గీచి దానిని 5 : 3 నిష్పత్తిలో (వృత్తలేఖని, స్కేలును ఉపయోగించి) విభజించండి.
సాధన.
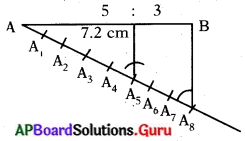
ప్రశ్న 7.
4.2 సెం.మీ., 5.1 సెం.మీ. మరియు 6 సెం.మీ. కొలతలతో త్రిభుజాన్ని నిర్మించండి. దీనితో సరూపంగా ఉంటూ ఈ త్రిభుజ భుజాలకు 2/3 రెట్లు అనురూప భుజాలు గల కొలతలతో త్రిభుజాన్ని నిర్మించండి.
సాధన.
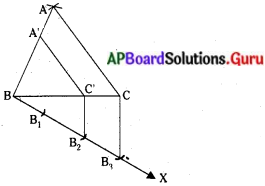
నిర్మాణం :
1. AB = 4.2 cm, BC = 5.1 cm, CA = 6 cm కొలతలతో ∆ABC నిర్మించితిని.
2. BCకు శీర్షం A ఉన్నవైపుకు వ్యతిరేక దిశలో అల్పకోణం చేయునట్లు BX కిరణమును గీచితిని.
3. BB1 = B1B2 = B2B3 అగునట్లు BX కిరణముపై B1, B2, B3 అనే మూడు బిందువులు గుర్తించితిని.
4. B3, C లను కలిపితిని. B3C కి సమాంతరంగా ఉండునట్లు B2C1 ను BC పై గీచితిని.
5. C1 నుండి CA కి సమాంతరంగా AB మీదకు ఒక రేఖ గీచితిని. అది AB ని A1 వద్ద ఖండించినది.
6. ∆A1BC1 కావలసిన త్రిభుజము.
![]()
ప్రశ్న 8.
QR = 5.5 సెం.మీ., ∠Q = 65°, PQ = 6 సెం.మీ. కొలతలు గల త్రిభుజం PQR ని నిర్మించి, దీనితో సరూపంగా వుంటూ, త్రిభుజ భుజాలకు 2/3 రెట్లు అనురూప భుజాల కొలతలు కలిగిన త్రిభుజాన్ని నిర్మించండి.
సాధన.
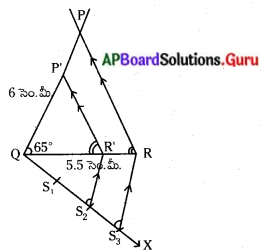
నిర్మాణక్రమము :
1) QR = 5.5 సెం.మీ., ∠Q = 65°, PQ = 6 సెం.మీ., కొలతలు గల ∆PQR నిర్మించితిని…
2) Q వద్ద ∠RQX అల్పకోణ కిరణం గీచితిని.
3) \(\overline{\mathrm{QX}}\) పై QS1 = S1S2 = S2S3 అగునట్లు S1, S2, S3 గుర్తించితిని.
4) S3 R కలిపితిని.
5) S3 R కు సమాంతరంగా S2 R’ మరియు PR కు సమాంతరంగా P’R’ గీచితిని. .
∴ ∆POR ~ ∆P’QR’.
![]()
ప్రశ్న 9.
(i) ప్రాథమిక అనుపాత సిద్ధాంతాన్ని ప్రవచించి, నిరూపించండి.
(ii) పై సిద్దాంతాన్ని ఉపయోగించి క్రింది పటంలో ఇవ్వబడిన AE పొడవును కనుగొనండి. AD = 1.8 సెం.మీ., BD = 5.4 సెం.మీ., EC = 7.2 సెం.మీ.
సాధన.
ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరు వేరు బిందువులలో ఖండించిన, ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజింపబడతాయి.
దత్తాంశము : ∆ABC లో DE || BC, DE రేఖ AB, AC భుజాలను వరుసగా D మరియు E వద్ద ఖండించును.
సారాంశము : \(\)
నిర్మాణము : B; E మరియు C, D లను కలుపుము మరియు DM ⊥ AC, EN ⊥ AB లను గీయుము.
ఉపపత్తి : ∆ADE వైశాల్యము = \(\frac{1}{2}\) × AD × EN
∆BDE వైశాల్యము = \(\frac{1}{2}\) × BD × EN
కావున 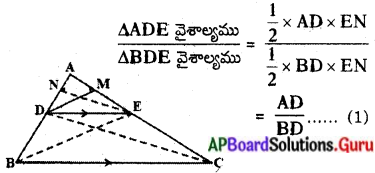
మరల ∆ADE వైశాల్యము = \(\frac{1}{2}\) × AE × DM
∆CDE వైశాల్యము = \(\frac{1}{2}\) × EC × DM
= \(\frac{\frac{1}{2} \times \mathrm{AE} \times \mathrm{DM}}{\frac{1}{2} \times \mathrm{EC} \times \mathrm{DM}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) …………….. (2)
∆BDE, ∆CDE లు ఒకే భూమి DE మరియు సమాంతర రేఖలు BC మరియు DE ల మధ్య ఉన్నట్లు గమనించవచ్చును.
కావున ∆BDE వైశాల్యము = ∆CDE వైశాల్యము …………….. (3)
(1), (2), (3) ల నుండి \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) కావున సిద్ధాంతము నిరూపించబడినది.
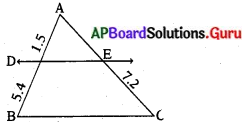
(ii) 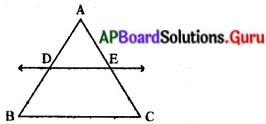
AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm
పై సిద్ధాంతమునుండి \(\frac{A D}{B D}=\frac{A E}{E C}\)
⇒ AE = \(\frac{(\mathrm{AD})(\mathrm{EC})}{\mathrm{BD}}=\frac{1.8 \times 7.2}{5.4}\) = 2.4
∴ AE = 2.4 సెం.మీ.
![]()
ప్రశ్న 10.
4.3 సెం.మీ., 5.2 సెం.మీ. మరియు 6.5 సెం.మీ. భుజాలుగా కల్గిన త్రిభుజాన్ని నిర్మించి, దానికి సరూపంగా ఉంటూ అనురూప భుజాలలో 3/5 భాగం కల్గిన వేరొక త్రిభుజాన్ని నిర్మించండి. …
సాధన.
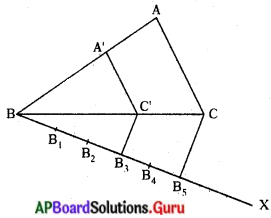
నిర్మాణం :
1. AB = 4.3 సెం.మీ., BC = 5.2 సెం.మీ. , CA = 6.5 సెం.మీ. కొలతలతో AABC నిర్మించితిని.
2. BC కు శీర్షం A ఉన్నవైపుకు వ్యతిరేక దిశలో అల్పకోణం చేయునట్లు BX కిరణమును గీచితిని.
3. BB1 = B1B2 = B2B3 = B3B4 = B4B5 అగునట్లు BX కిరణముపై B1, B2, B3, B4, B5. అనే ఐదు బిందువులు గుర్తించితిని.
4. B5, C లను కలిపితిని: B3C కి సమాంతరంగా ఉండునట్లు B, C’ను BC పై గీచితిని.
5. C’ నుండి CA కి సమాంతరంగా AB మీదకు ఒక రేఖ గీచితిని అది ABని A’ వద్ద ఖండించినది.
6. ∆A’BC’ కావలసిన త్రిభుజము.
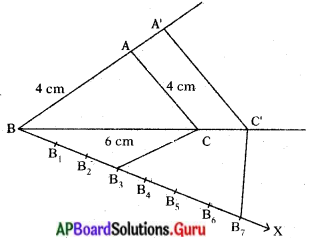
ప్రశ్న 11.
AB = 4 సెం.మీ., BC = 6 సెం.మీ. మరియు AC = 4 సెం.మీ. కొలతలు గల త్రిభుజం ABC, నిర్మించుము. ఈ త్రిభుజానికి సరూపంగా ఉంటూ, ఈ త్రిభుజ భుజాలకు 3/4 రెట్లు అనురూప భుజాల కొలతలు కలిగిన త్రిభుజాన్ని నిర్మించండి.
సాధన.