SCERT AP 8th Class Maths Solutions Chapter 6 వర్గమూలాలు, ఘనమూలాలు Ex 6.2 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 6th Lesson వర్గమూలాలు, ఘనమూలాలు Exercise 6.2
ప్రశ్న1.
ప్రధాన కారణాంకాల పద్ధతిని ఉపయోగించి క్రింది వాటి వర్గమూలాలు కనుగొనుము.
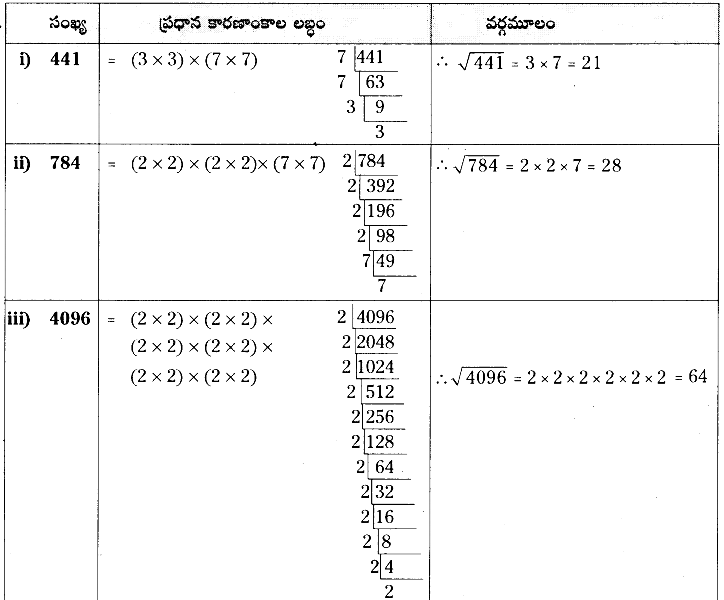
(i) 441
(ii) 784
(iii) 4096
(iv) 7056
సాధన.

![]()
ప్రశ్న2.
3645 ని ఏ కనిష్ఠ సంఖ్యచే గుణించిన పరిపూర్ణ వర్గం అగును ?
సాధన.
3645 యొక్క ప్రధాన కారణాంకాల లబ్దం = (3 × 3) × 5 × (3 × 3) × (3 × 3)
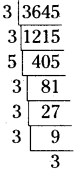
ఒక ‘5’ లోపించినది కావునా
3645 ను 5చే గుణించిన పరిపూర్ణ వర్గం అగును.
ప్రశ్న3.
2400 ని ఏ కనిష్ఠ సంఖ్యచే గుణించగా పరిపూర్ణ వర్గం అగును ? వచ్చిన ఫలిత సంఖ్య వర్గమూలం కనుగొనుము.
సాధన.
2400 యొక్క ప్రధాన కారణాంకాల లబ్దం
= (2 × 2) × (2 × 2) × 2 × (5 × 5) × 3
∴ పై లబ్దాల జతలలో 2, 3లు లోపించినవి కావునా 2 × 3 = 6 చే గుణించగా 2400 పరిపూర్ణ వర్గ సంఖ్య అగును.
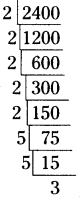
∴ 2400 × 6 = (2 × 2) × (2 × 2) × (2 × 2) × (5 × 5) × (3 × 3)
⇒ \(\sqrt{14400}\) = 2 × 2 × 2 × 5 × 3
= 120
ప్రశ్న4.
7776 ను ఏ కనిష్ఠ సంఖ్యచే భాగించగా పరిపూర్ణ వర్గం అగును ?
సాధన.
7776 యొక్క ప్రధాన కారణాంకాల లబ్దం

= (2 × 2) × (2 × 2) × 2 × (3 × 3) × (3 × 3) × 3
∴ 7776 పరిపూర్ణ వర్గ సంఖ్య.
కావలెనన్న దానిని 2 × 3 = 6 చే భాగించవలెను.
![]()
ప్రశ్న5.
ఒక తోటలో ఉన్న 1521 చెట్లు కొన్ని వరుసలలో కలవు. ప్రతి వరుసలో ఉన్న చెట్ల సంఖ్య, వరుసల సంఖ్యకు సమానం. అయిన ప్రతి వరుసలోని చెట్ల సంఖ్య, తోటలోని వరుసల సంఖ్య కనుక్కోండి.
సాధన.
తోటలోని ఒక్కొక్క వరుసలో ఉన్న చెట్ల సంఖ్య = x అనుకొనుము.
తోటలోని వరుసల సంఖ్య = x
తోటలో గల మొత్తం చెట్ల సంఖ్య = x × x = x2
లెక్క ప్రకారం తోటలో గల చెట్ల సంఖ్య = 1521
∴ x2 = 1521
x = \(\sqrt{1521}\) = \(\sqrt{39 \times 39}\) = 39
∴ ఆ తోటలోని ఒక్కొక్క వరుసకు గల చెట్ల సంఖ్య = 39
∴ ఆ తోటలోని వరుసల సంఖ్య = 39
ప్రశ్న6.
ఒక పాఠశాలలో విద్యార్థుల నుండి ఫీజు రూపంలో ₹ 2601 వసూలు చేశారు. పాఠశాలలోని విద్యార్థుల సంఖ్య, ప్రతి విద్యార్థి చెల్లించిన ఫీజుకి సమానం అయిన విద్యార్థుల సంఖ్య ఎంత ?
సాధన.
పాఠశాలలోని విద్యార్థుల సంఖ్య = x అనుకొనుము.
ప్రతి విద్యార్థి చెల్లించిన ఫీజు = ₹ x
∴ పాఠశాల మొత్తం మీద వసూలైన ఫీజు x × x = x2
లెక్క ప్రకారం
పాఠశాలకు ఫీజు రూపంలో వచ్చినది = 2601
∴ x2 = 2601
∴ x = \(\sqrt{2601}\) = \(\sqrt{51 \times 51}\) = 51
∴ ఆ పాఠశాలలోని విద్యార్థుల సంఖ్య = 51
ప్రశ్న7.
రెండు సంఖ్యల లబ్ధం 1296. వాటిలో మొదటి సంఖ్య, రెండవ సంఖ్యకు 16 రెట్లు అయిన ఆ రెండు సంఖ్యలు ఏవి?
సాధన.
రెండవ సంఖ్య = x అనుకొనుము.
మొదటి సంఖ్య = 16x
రెండు సంఖ్యల లబ్దం = 16 x × x = 16x2
లెక్క ప్రకారం
⇒ 16x2 = 1296
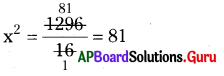
x2 = 81
x = \(\sqrt{81}\) = \(\sqrt{2601}\) = 9
∴ మొదటి సంఖ్య = 16x = 16 × 9 = 144
రెండవ సంఖ్య (x) = 9
![]()
ప్రశ్న8.
7921 మంది సైనికులు ఒక సమావేశమందిరం (ఆడిటోరియం) లో కొన్ని వరుసలలో కూర్చొని ఉన్నారు. ప్రతి వరుసలోని సైనికుల సంఖ్య, వారు కూర్చున్న వరుసల సంఖ్యకు సమానం. అయిన సమావేశమందిరంలో ఉన్న వరుసల సంఖ్య ఎంత?
సాధన.
ప్రదర్శనశాలలోని సైనికుల సంఖ్య = x అనుకొనుము.
సైనికులు కూర్చొను వరుసల సంఖ్య = x
మొత్తం సైనికుల సంఖ్య = x × x = x2
లెక్క ప్రకారం
x2 = 7921
x = \(\sqrt{7927}\) = \(\sqrt{89 \times 89}\) = 89
∴ ఆ సమావేశమందిరంలోని వరుసల సంఖ్య = 89
ప్రశ్న9.
ఒక చతురస్రాకార పొలం వైశాల్యం 5184 మీ2. చతురస్రపు చుట్టుకొలతకు సమాన చుట్టుకొలత గల దీర్ఘచతురస్రం కలదు. దీర్ఘ చతురస్రం యొక్క పొడవు, వెడల్పుకు రెట్టింపు అయిన దీర్ఘచతురస్ర వైశాల్యం ఎంత ?
సాధన.
చతురస్ర వైశాల్యం = 5184
A = s2 = 5184
⇒ s = \(\sqrt{5184}\) = \(\sqrt{72 \times 72}\) = 72
∴ చతురస్ర భుజం (s) = 72 మీ.
చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 72 = 288 మీ.
దీర్ఘచతురస్ర చుట్టుకొలత = చతురస్ర చుట్టుకొలత
దీర్ఘ చతురస్ర వెడల్పు = x మీ. అనుకొనుము.
పొడవు = 2 × x = 25 మీ.
దీ॥చ॥ చుట్టుకొలత = 2(l + b)
⇒ 2(2x + x) = 288
3x = 144
x = 48
∴ దీర్ఘచతురస్ర వెడల్పు = 48 మీ.
పొడవు = 2x = 2 × 48 = 96 మీ.
∴ దీర్ఘచతురస్ర వైశాల్యం = పొడవు × వెడల్పు
= 96 × 48
= 4608 మీ2.